pthread 变量静态初始化 避免使用被销毁过的变量
pthread 变量静态初始化
- 互斥锁:
pthread_mutex_t g_mutex = PTHREAD_MUTEX_INITIALIZER; - 读写锁:
pthread_rwlock_t g_rwlock = PTHREAD_RWLOCK_INITIALIZER; - 条件变量:
pthread_cond_t g_cond = PTHREAD_COND_INITIALIZER;
适用场景
- 以互斥锁为例,当持有互斥锁的线程,需要进行互斥锁的销毁工作时,无法确保当前没有任何其他线程会在锁销毁之后,仍使用该锁。
场景代码
-
模块 xx 对外提供3个 api,分别为打开,关闭,资源获取,资源获取接口以及关闭接口可能会被外部不同的线程调用,因此需要使用互斥锁保护,如果关闭接口先于资源获取接口获得互斥锁,且关闭接口中执行了互斥锁的销毁,则会导致阻塞在资源获取接口上的线程使用被销毁过的互斥锁。
-
代码如下:
#include <pthread.h>pthread_mutex_t mutex;int xx_init() {pthread_mutex_init(&mutex, NULL);// ... }int xx_getres() {pthread_mutex_lock(&mutex);// ...pthread_mutex_unlock(&mutex); }int xx_close() {pthread_mutex_lock(&mutex);// ...pthread_mutex_unlock(&mutex);pthread_mutex_destroy(&mutex); }
解决方案
-
第一种方案就是控制外部调用,保证在调用关闭接口之前,没有任何其他线程阻塞在资源获取接口上。
-
第二种方案就是使用静态初始化,代码如下:
#include <pthread.h>pthread_mutex_t mutex = PTHREAD_MUTEX_INITIALIZER;int xx_init() {// ... }int xx_getres() {pthread_mutex_lock(&mutex);// ...pthread_mutex_unlock(&mutex); }int xx_close() {pthread_mutex_lock(&mutex);// ...pthread_mutex_unlock(&mutex); }
相关文章:

pthread 变量静态初始化 避免使用被销毁过的变量
pthread 变量静态初始化 互斥锁:pthread_mutex_t g_mutex PTHREAD_MUTEX_INITIALIZER;读写锁:pthread_rwlock_t g_rwlock PTHREAD_RWLOCK_INITIALIZER;条件变量:pthread_cond_t g_cond PTHREAD_COND_INITIALIZER; 适用场景 以互斥锁为例…...

深度学习之基于ResNet18的神经网络水果分类系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介二、功能三、神经网络水果分类系统四. 总结 一项目简介 基于ResNet18神经网络的水果分类系统是一个利用深度学习技术进行水果图像分类的系统。下面是该系统…...

并查集易错点
并查集就俩核心点,1是找父节点,2是合并 1: return fa[x] x ? x : fa[x] find(fa[x]); 2. fa[find(a)] find(b) 第二步还挺容易写错的,左边是find(a)的根,而不是fa[a]...

车载网关产品解析(附:车载网关详细应用案例及部署流程)
5G车载网关是一款功能强大的工业级无线通讯设备。它集成了4G/5G双模网络模块、M12接口设计、强大的路由和安全功能等特性,可以为车载和移动应用提供稳定可靠的无线数据连接。 链接直达:https://www.key-iot.com/iotlist/sv900.html ### 产品特性 5G车载网关最大的…...

高校教务系统登录页面JS分析——天津大学
高校教务系统密码加密逻辑及JS逆向 本文将介绍天津大学教务系统的密码加密逻辑以及使用JavaScript进行逆向分析的过程。通过本文,你将了解到密码加密的基本概念、常用加密算法以及如何通过逆向分析来破解密码。 本文仅供交流学习,勿用于非法用途。 一、密…...
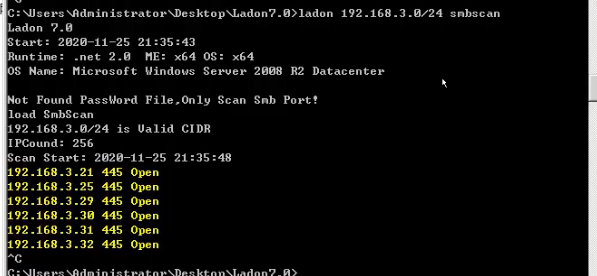
68 内网安全-域横向PTHPTKPTT哈希票据传递
目录 演示案例:域横向移动PTH传递-Mimikatz域横向移动PTK传递-Mimikatz域横向移动PTT传递-MS14068&kekeo&local国产Ladon内网杀器测试验收-信息收集,连接等 涉及资源: PTH(pass the hash) #利用lm或ntlm的值进行的渗透测试 PTT(pass the ticket) #利用的票据凭证TGT进行…...

【1】2023版密评算分工具
0X01 前言 工具根据商用密码应用安全性评估量化评估规则(2023年8月1日实施)实现 0x02 工具功能介绍 给定D A K的打分结果,计算单个测评对象和测评单元得分。根据测评单元得分计算测评层面得分根据测评层面得分计算报告整体得分配置文件说明…...

人工智能常用网站
ModelScope - 模型列表页 https://huggingface.co/models...

OpenLayers实战,OpenLayers结合下拉菜单实现城市切换,动态切换城市边界到地图视图视角范围内
专栏目录: OpenLayers实战进阶专栏目录 前言 本章是OpenLayers综合实战案例,使用OpenLayers结合下拉菜单实现城市切换,动态切换城市边界到地图视图视角范围内。 本章需要使用到ElementUI的下拉框组件和OpenLayers的TopoJson格式解析地市边界数据并负责渲染,通过动态创建s…...
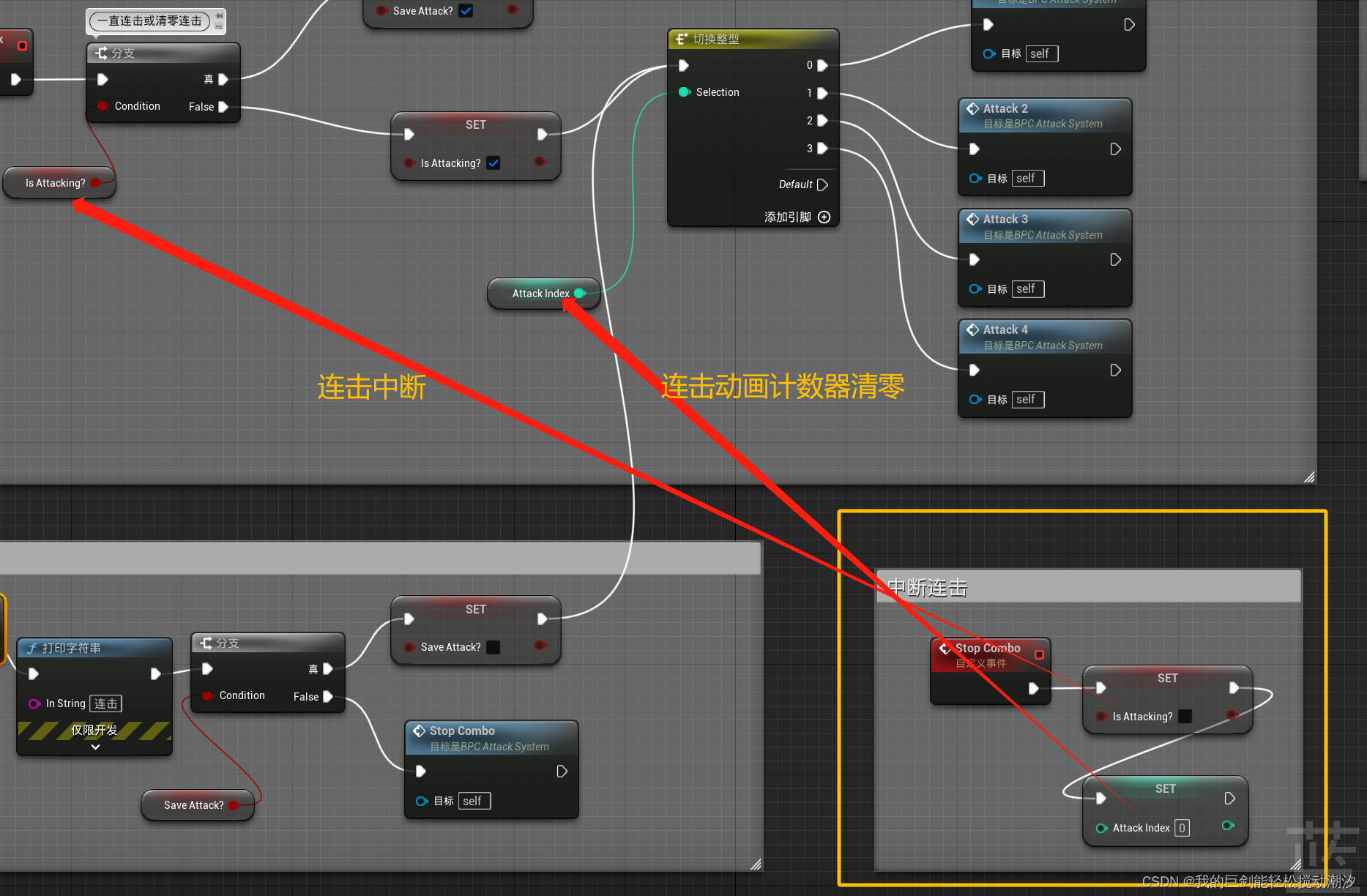
UE5 日记(人物连招:蒙太奇动画通知(含视频链接))
教程https://www.youtube.com/watch?vsWpENaVGj2M&listPLiSlOaRBfgkcPAhYpGps16PT_9f28amXi&index10&ppiAQB 相关蓝图 连招逻辑 动画通知类 逻辑分析 1.用户输入 已搭载战斗系统模块,可以收到输入指令 2.连击 第一次攻击: 第一次攻击,…...

葡萄酒是如何从葡萄园到你的酒杯的?
根据定义,我们称葡萄酒的美味花蜜是葡萄酒精发酵的产物。也有果酒,或乡村酒,是由发酵的水果制成的。然而,传统意义上的葡萄酒是由酿酒葡萄制成的。好吧,一切都是在几个步骤中完成的,来自云仓酒庄品牌雷盛红…...
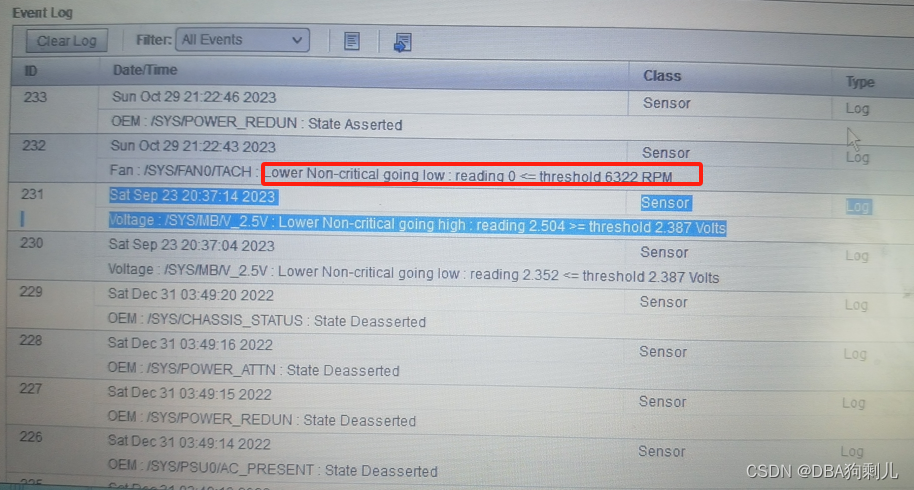
Oracle Exadata X7-2掉电宕机导致集群无法启动处理过程
文章目录 前言一、当前的状态是什么?二、集群启动异常怀疑对象1.排查心跳网络异常ping自己私有IP延迟高ping其它主机私有IP不通 2.是否发生过重启 三、日志信息收集ocssd.trc集群crs日志cell的griddisk状态及报错 四、IB交换机的问题排查处理五、紧急恢复业务在IB完…...
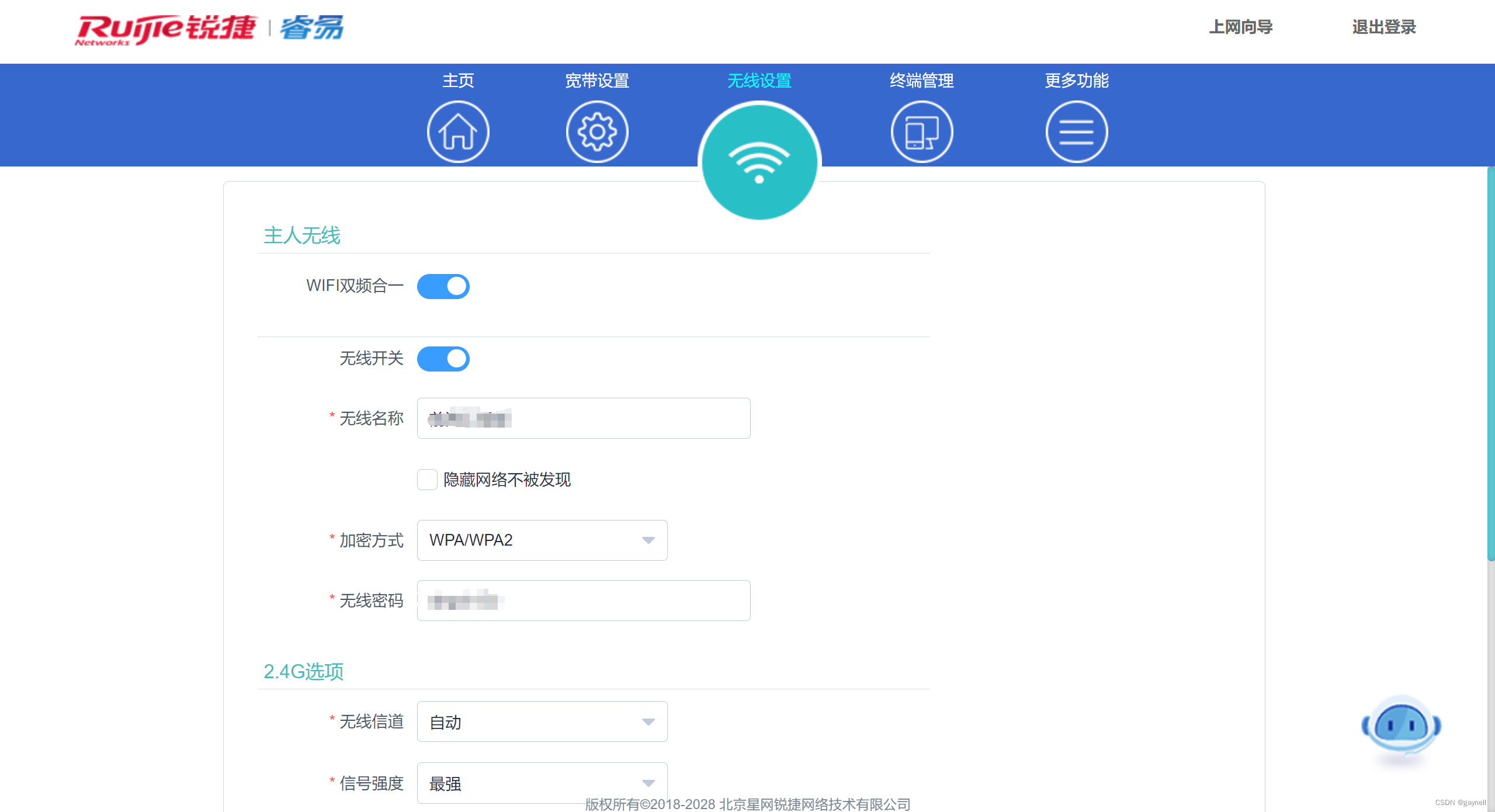
锐捷RG-EW1200G登录绕过漏洞复现
文章目录 锐捷RG-EW1200G登录绕过漏洞复现0x01 前言0x02 漏洞描述0x03 影响版本0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.复现 0x06 修复建议 锐捷RG-EW1200G登录绕过漏洞复现 0x01 前言 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、…...

Python之循环语句
循环普遍存在于日常生活中,同样,在程序中,循环功能也是至关重要的基础功能。 循环在程序中同判断一样,也是广泛存在的,是非常多功能实现的基础 while循环的基础语法 生活中的循环 程序中的循环 只要条件满足 会无限循…...

python中使用websocket调用、获取、保存大模型API
笔者最近在测试星火大模型的时候,他们是使用websocket 来建立对话,而且星火大模型开放的测试代码,质量上不咋地(20231030记录),还需要对websocket有一定的了解,才适合自己微调。 安装ÿ…...
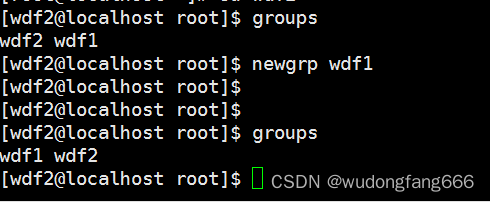
Linux的账号管理
本章的学习感觉如果不做系统管理员,作为简单了解就可以了 前面介绍了,用户,组,other三个角色, 每个用户创建都会有uid与之对应,创建的用户基本信息在一下两个文件中,也是我们要介绍的内容&…...

优优嗨聚集团:医保新政来袭,乙类OTC、保健品或将退出医保舞台,影响几何?
近日,国家医保局发布征求意见稿,拟将乙类OTC(非处方药)和保健品从医保目录中移除。这一政策一旦实施,无疑将对广大参保人员和相关企业产生深远影响。本文将为您详细解析这一政策可能带来的影响,以及如何应对…...

ubuntu安装pandora-gpt
因为pandora要3.7以上的版本,推荐MINICANDA, 1,在清华镜像网站上下载miniconda3安装的脚本文件 sudo wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/miniconda/Miniconda3-py38_4.9.2-Linux-x86_64.sh2,给.sh文件添加x执…...

PHP校验身份证号是否正确
用PHP语言实现校验身份证号的算法,供参考 /*** 校验身份证号是否正确* param $idcard 身份证号* return bool true正确*/public static function validateIDCard($idcard) {if(empty($idcard)){return false;}if (!preg_match(/(^\d{15}$)|(^\d{17}([0-9]|X|x)$)/,$…...
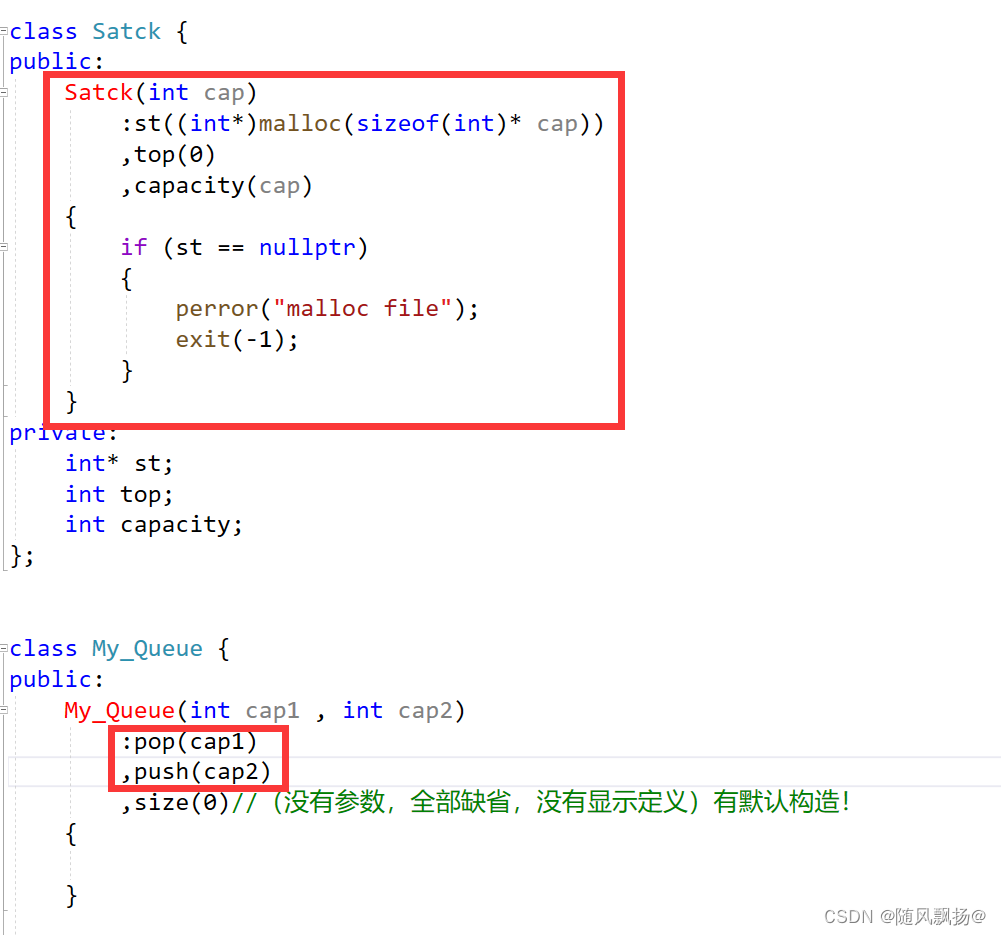
[C++ ]:5.类和对象中(运算符重载补充)+ 类和对象下(初始化列表)
类和对象中(运算符重载补充) 类和对象下(初始化列表) 一.运算符重载补充:1.流插入运算符:1.考虑到隐含的参数指针:2.进行优化!2-1:解决办法:友元2-2ÿ…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
