[补题记录] Codeforces Round 906 (Div. 2)(A~D)
URL:https://codeforces.com/contest/1890
目录
A
Problem/题意
Thought/思路
Code/代码
B
Problem/题意
Thought/思路
Code/代码
C
Problem/题意
Thought/思路
Code/代码
D
Problem/题意
Thought/思路
Code/代码
A
Problem/题意
给出一个数组 A,你可以将它任意排列,问是否能使得
Thought/思路
化简题目给的要求,我们可以发现:
- a1 = a3、a3 = a5;
- a2 = a4、a4 = a6;
因此只要有第三种数出现,肯定不对。
两种数的数量不等,也不对。
特别要注意,只有一种数则直接正确。
Code/代码
#include "bits/stdc++.h"int n, a[107];void solve() {std::cin >> n;std::set <int> num;std::map <int, int> cnt;bool flag = true;for (int i = 1; i <= n; ++ i) {std::cin >> a[i];num.insert(a[i]);if (num.size() > 2) {flag = false;} else {cnt[a[i]] ++;}}if (num.size() == 1) {std::cout << "Yes\n";return;}if (flag) {int a = *num.begin(); num.erase(a);int b = *num.begin();if (n % 2 == 1) {if (std::abs(cnt[a] - cnt[b]) == 1) {std::cout << "Yes\n";} else {std::cout << "No\n";}} else {if (cnt[a] == cnt[b]) {std::cout << "Yes\n";} else {std::cout << "No\n";}}} else {std::cout << "No\n";}
}signed main() {int t; std::cin >> t;while (t--) {solve();}
}B
Problem/题意
给出 2 个 01 字符串 S、T。当字符串满足 ,则这个字符串为 good。
你可以将 T 插入 S 的任意位置(也可以不插),问能否使得 S 为 good。
Thought/思路
如果 S 是 good,直接输出答案 YES。
如果 S 不是 good,那么 T 必须要为 good,否则直接输出答案 NO。
当 S 不是 good 时,说明遇到了 ,此时:
- 如果 Si = 0,那么 T 必须要满足头尾都是 1;
- 如果 Si = 1,那么 T 必须要满足头尾都是 0;
所以可以得出:
- 若 T 头尾不相同,直接输出答案 NO;
- 若需要插入时,Si != T[0],直接输出答案 NO;
经过以上判断后,则输出 YES。
Code/代码
#include "bits/stdc++.h"int n, m;
std::string s, t;void solve() {std::cin >> n >> m;std::cin >> s >> t;bool flag = true;for (int i = 0; i <= n - 2; ++ i) {if (s[i] == s[i + 1]) {flag = false;}}if (flag) {std::cout << "YES\n";return;}for (int i = 0; i <= m - 2; ++ i) {if (t[i] == t[i + 1]) {std::cout << "NO\n";return;}}if (t[0] != t[m - 1]) {std::cout << "NO\n";return;}for (int i = 0; i <= n - 2; ++ i) {if (s[i] == s[i + 1]) {if (s[i] == t[0]) {std::cout << "NO\n";return;}}}std::cout << "YES\n";
} signed main() {int t; std::cin >> t;while (t --) {solve();}
} C
Problem/题意
给出 1 个 01 字符串 S。当字符串满足 ,则这个字符串为 good。
你可以将 "01" 插入 S 的任意位置(也可以不插),位置可以从 0 开始。
问能否使得 S 为 good。
若能,输出插入序列,若不能,输出 -1。
Thought/思路
因为要求对称位置不相等,所以 n 为奇数时,直接输出 -1。
因为每次插入的是 01,因此若一开始 01 数量不相等,直接输出 -1。
考虑到,若当前 i 之前的位置,都已经与对称位置不同,那么在 [i, n - i + 1] 中任意位置插入,都不会对前面的插入有影响,因此我们直接 L、R 双指针判断即可。
当对称位相等时,说明需要插入 01,此时有:
- 若 S[L] = 1,说明必须将 01 插入到 L 的左边;
- 若 S[L] = 0,说明必须将 01 插入到 R 的右边;
插入后就是移动 L、R,以及拼接新字符串了,可以自己想一下。
Code/代码
#include "bits/stdc++.h"int n;
std::string s;void solve() {std::cin >> n >> s;s = "#" + s;if (n % 2 == 1) {std::cout << -1 << "\n";return;}std::map <int, int> cnt;for (int i = 1; i <= n; ++ i) {cnt[s[i] - '0'] ++;}if (cnt[0] != cnt[1]) {std::cout << -1 << "\n";return;}std::vector <int> ans;int l = 1, r = n;while (l + 1 != r) {if (s[l] == s[r]) {if (s[l] == '1') {ans.push_back(l - 1);std::string a = s.substr(1, l - 1);std::string b = s.substr(l, n - l + 1);//std::cout << "a=" << a << " b=" << b << " ";s = "#" + a + "01" + b;l ++;r += 2; r --;}else if (s[l] == '0') {ans.push_back(r);std::string a = s.substr(1, r);std::string b = s.substr(r + 1, n - (r + 1) + 1);//std::cout << "a=" << a << " b=" << b << " ";s = "#" + a + "01" + b;r += 2; r --;l ++;}n += 2;} else {l ++;r --;}//std::cout << "l=" << l << " r=" << r << " s=" << s << "\n";}std::cout << ans.size() << "\n";for (auto x : ans) std::cout << x << " ";std::cout << "\n";
}signed main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);int t; std::cin >> t;while (t --) solve();
}D
Problem/题意
一个国家有 N 个城市,每个城市有 Ai 人,现在要为这个国家修路,当我们想连接城市 i 和城市 j 时,有一个整数 C,需要满足:
- 令城市 i 和它已经连通的城市,总人口为 Si;
- 令城市 j 和它已经连通的城市,总人口为 Sj;
- 当 Si + Sj >= i * j * C 时,则可以在 i 和 j 之间修路;
问能否将 N 个城市连通。
Thought/思路
很容易想到,当我们使用城市 1 去连接其他城市时,更加容易成功。
需要考虑的是:怎么知道用 1 连接完它能连接的城市后,就已经是最大能连接的数量了。
假设现在有城市 X、Y,它们之间可以连接,则有:
若它们不能与城市 1 连接,则有:
将三条不等式整合,可得:
↓
↓
但是 X、Y 显然是大于 1 的,该不等式不成立。
因此 X、Y 若能连接,则它们一定可以和城市 1 相连。
回到我们最开始的想法:使用城市 1 去连接其他城市时,更加容易连接成功。因此我们可以使用 i * C - A[i] 升序排序,排在前面的更容易与 1 相连。
假设此时 1 已经连接了一些城市,遇到一个城市 M,若 1 不能与城市 M 相连,那么就一定失败了,因为:
- 若 M 都不能与 1 相连,那 M 后面的城市也一定不能与 1 相连;
- 既然 M 后面的城市连 1 都连不上,那么肯定也连不上 1 已经连上的城市;
这也是可以证明的,根据上面的条件,假设 M 不能与 1 相连,N 为 M 后的城市,则有:
最后得出:
↓
↓
Code/代码
#include "bits/stdc++.h"#define int long longstruct node {int id, v;bool operator < (const node &t) const {return v < t.v;}
};int n, c, a[200007];void solve() {std::cin >> n >> c;std::vector <node> s(n + 1);for (int i = 1; i <= n; ++ i) {std::cin >> a[i];s[i] = {i, i * c - a[i]};}std::sort(s.begin() + 2, s.end());int sum = a[1];bool flag = true;for (int i = 2; i <= n; ++ i) {int id = s[i].id;sum += a[id];if (sum < id * c) flag = false;} if (flag) std::cout << "YES\n";else std::cout << "NO\n";
}signed main() {int t; std::cin >> t;while (t --) solve();return 0;
}相关文章:
[补题记录] Codeforces Round 906 (Div. 2)(A~D)
URL:https://codeforces.com/contest/1890 目录 A Problem/题意 Thought/思路 Code/代码 B Problem/题意 Thought/思路 Code/代码 C Problem/题意 Thought/思路 Code/代码 D Problem/题意 Thought/思路 Code/代码 A Problem/题意 给出一个数组 A…...

Kubernetes yaml文件
目录 yaml文件 Pod yaml文件详解 deployment.yaml文件详解 Service yaml文件详解 文件 Kubernetes 支持 YAML 和 JSON 格式管理资源对象 JSON 格式:主要用于 api 接口之间消息的传递 YAML 格式:用于配置和管理,YAML 是一种简洁的非标记性…...
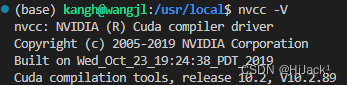
Linux——切换CUDA版本
一、查看本地cuda版本 cd /usr/local/ ls当前cuda为软连接,指向指定的cuda版本 stat cuda # 查看当前cuda状态信息二、切换CUDA版本 # 删除原有软连接 sudo rm -rf /usr/local/cuda # 建立需要切换的cuda软连接版本 sudo ln -s /usr/local/cuda-**.* /usr/l…...

利用云计算和微服务架构开发可扩展的同城外卖APP
如今,同城外卖APP已经成为了人们点餐的主要方式之一。然而,要构建一款成功的同城外卖APP,不仅需要满足用户的需求,还需要具备可扩展性,以适应快速增长的用户和订单量。 一、了解同城外卖APP的需求 在着手开发同城外卖…...
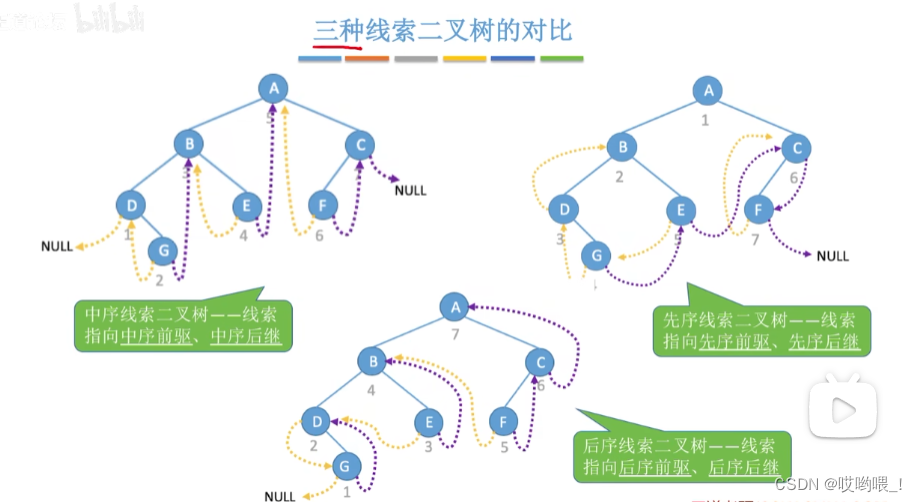
数据结构详细笔记——二叉树
文章目录 二叉树的定义和基本术语特殊的二叉树满二叉树完全二叉树二叉排序树平衡二叉树 二叉树的常考性质完全二叉树的常考性质二叉树的存储结构顺序存储链式存储 二叉树的先中后序遍历先序遍历(空间复杂度:O(h))中序遍…...
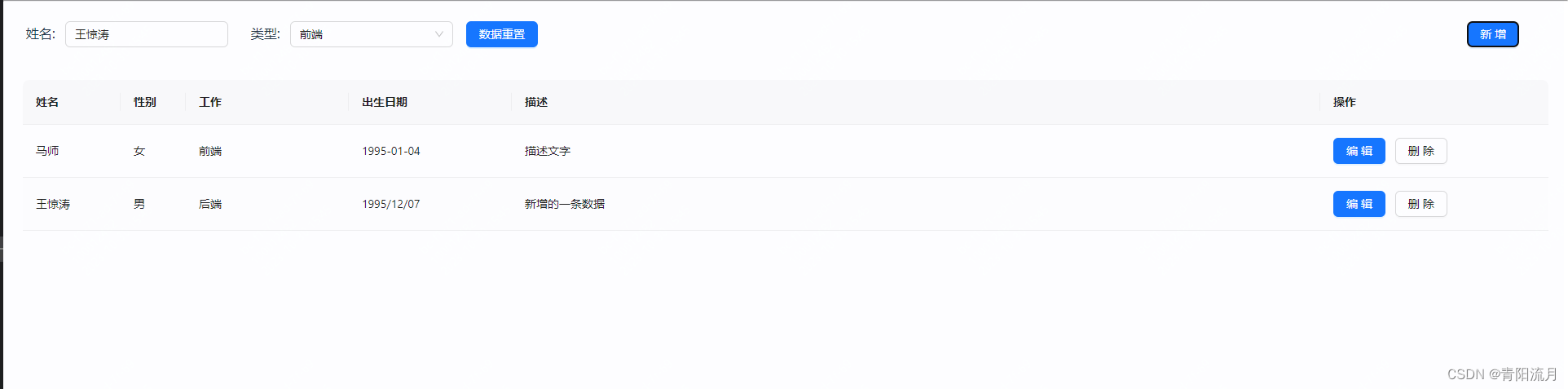
react实现列表增删改查的小demo(class组件版)
前言 react的语法上就是比vue麻烦不少,既然要开手动挡,那就开吧,一个基础的demo 效果图 列表 新增弹窗 编辑弹框 新增一条数据后的效果 代码 根组件 index.jsx import React, { Component,createRef} from react import withRouter from ../../utils/withRouter import G…...
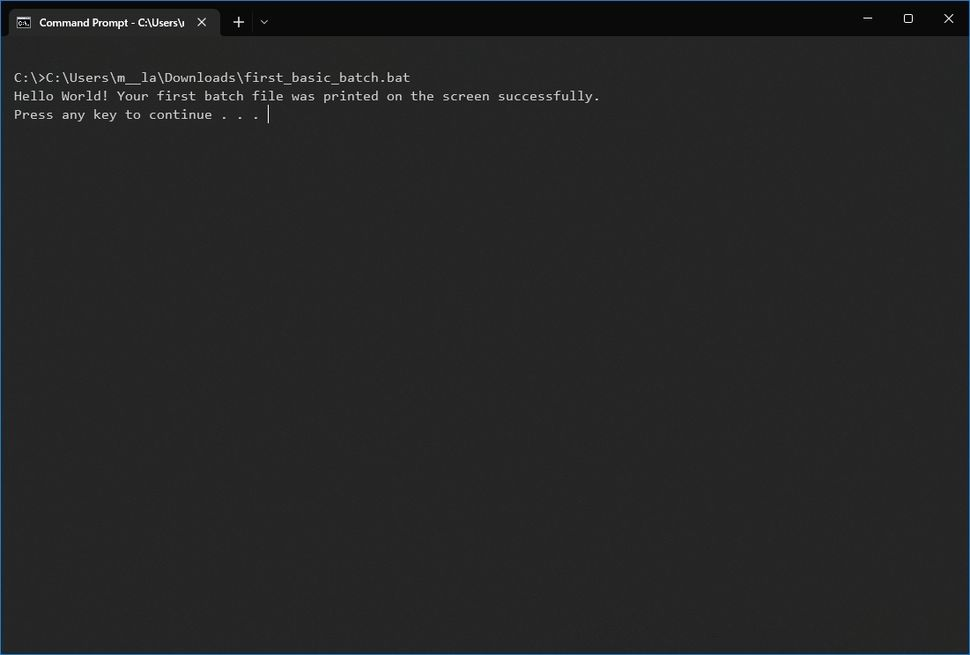
运行批处理文件,Windows 10至少提供了三种方法,有的可以设置定时运行
Windows 10至少有三种写入批处理文件的方法。你可以使用命令提示符或文件资源管理器按需运行它们。你可以使用任务计划程序配置脚本,以便按计划运行。或者,你可以将批处理文件保存在“启动”文件夹中,让系统在你登录帐户后立即运行它们。 如果要按需运行脚本,可以使用文件…...

C++ detach线程的归属权和控制权交给runtime library的原因
在C中,std::thread的detach操作将线程的归属权和控制权都转移给了C运行时库(runtime library)。这是因为detach操作的目的是告诉C运行时库,你不再关心这个线程的状态,它可以在后台独立运行,而不需要等待主线…...
Android应用集成RabbitMQ消息处理指南
Android应用集成RabbitMQ消息处理指南 RabbitMQ1、前言2、RabbitMQ简介2.1、什么是RabbitMQ2.2、RabbitMQ的特点2.3、RabbitMQ的工作原理2.4、RabbitMQ中几个重要的概念 3、在Android Studio中集成RabbitMQ3.1、在Manifest中添加权限:3.2、在build.gradle(:app)下添…...

爆改86㎡户型,中式禅意,自然诗意!福州中宅装饰,福州装修
自然诗意 中式禅意 东方风韵,涟漪泛晕。 ——致生活感的“空间”,最美的家 案例简介 作品:泛晕 风格:新中式 面积:86平方 楼盘:长乐中南樾府 中国风与现代风混搭 木元素是中国风表达中最具灵魂般的存…...
LVGL库入门 02 - 布局
1、简单布局 可以使用 lv_obj_set_pos(obj, x, y) 调整一个控件的位置(或者使用类似的函数单独调整一个方向的坐标),将它放在相对父容器左上角的合适位置。不过这种布局方式非常死板,因为绝对坐标一旦设定就不能自动调整…...
利用Vue2实现印章徽章组件
需要实现的组件效果: 该组件有设置颜色、大小、旋转度数和文本内容功能。 一、组件实现代码 <template><divclass"first-ring"v-bind"getBindValue":class"getStampBadgeClass":style"{ transform: rotate(${rotate}…...

金麟国际用工-全新蓝领跨境就业服务平台
金麟国际用工-全新蓝领跨境就业服务平台 金麟国际用工平台是一个引领时代的蓝领跨境就业服务平台,专为蓝领求职者和雇主提供一个全面、便捷、高效的就业对接环境。这个平台通过其强大的数字化系统,包括客户管理系统、岗位信息系统和智能营销工具等&…...

性能测试知多少---并发用户
在做性能测试的时候,我们常常听到并发用户、响应时间、吞吐量专业术语,也许大家都理解,这里有一个理解的层次与深度概念。最近有看断念《软件性能详解与案例分析》一书,看了他的讲解,原来我对这些术语的理解还是比较肤…...
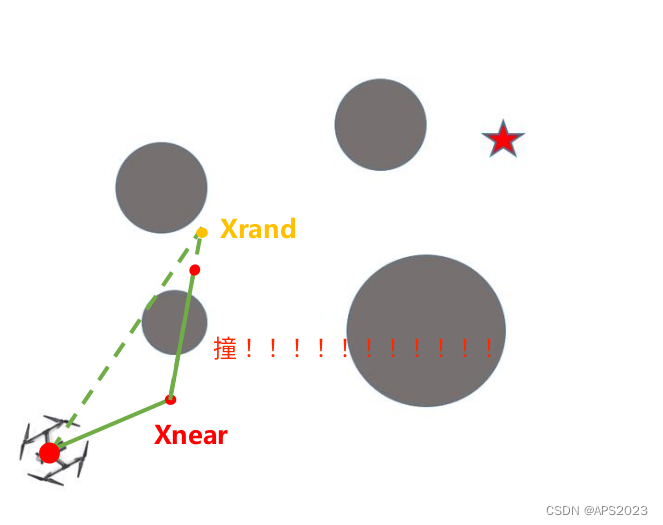
自动驾驶算法(三):RRT算法讲解与代码实现(基于采样的路径规划)
目录 1 RRT算法原理 2 RRT算法代码解析 3 RRT完整代码 1 RRT算法原理 RRT算法的全称是快速扩展随机树算法(Rapidly Exploring Random Tree),它的想法就是从根结点长出一棵树当树枝长到终点的时候这样就能找到从终点到根节点的唯一路径。 算法流程: 首先…...
基于SSM的酒店客房预定管理系统
基于SSM的酒店客房预定管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatis工具:IDEA/Ecilpse、Navicat、Maven 系统展示 前台主页 客房详情 登录界面 管理员界面 用户界面 摘要 基于SSM(…...
IDEA初步入门
1 安装 现在的系统更迭很快,很多软件都只支持win10 和 11了,但我们过时党还在用win7. 所以就必须找到合适的版本。在windows 7 64位系统下,可以使用IDEA 2020.1.4版本。 在Jetbrain官方下,找到历史版本,找到windows版…...

《Webpack 5 基础配置》- 禁止在出现编译错误或警告时,覆盖浏览器全屏显示
Webpack5 overlay 配置地址默认编译错误或警告为 true,即浏览器全屏显示;overlay 属性可以是 boolean 型,也可是 object 类型;还有其它设置说明,详见上述官网地址; module.exports {devServer: {client: {…...

echart 饼图怎么让图形铺满整个div
1.原效果(未铺满):原配置 2.如果想要铺满,需要设置radius ,radius的意思是 第一个元素为内环半径,第二个参数为外环半径; 如果想要填满的话直接写[0,100%],不过第一个为0后就不是圆环里&#…...

回归预测 | Matlab实现WOA-CNN-SVM鲸鱼算法优化卷积神经网络-支持向量机的多输入单输出回归预测
回归预测 | Matlab实现WOA-CNN-SVM鲸鱼算法优化卷积神经网络-支持向量机的多输入单输出回归预测 目录 回归预测 | Matlab实现WOA-CNN-SVM鲸鱼算法优化卷积神经网络-支持向量机的多输入单输出回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.WOA-CNN-SVM鲸鱼算法…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
