Opencv实现的三次样条曲线(Cubic Spline)插值
1.样条曲线简介
样条曲线(Spline)本质是分段多项式实函数,在实数范围内有: S:[a,b]→R ,在区间 [a,b] 上包含 k 个子区间[ti−1,ti],且有:
a=t0<t1<⋯<tk−1<tk=b(1)
对应每一段区间 i 的存在多项式: Pi:[ti−1,ti]→R,且满足于:
S(t)=P1(t) , t0≤t<t1,S(t)=P2(t) , t1≤t<t2,⋮S(t)=Pk(t) , tk−1≤t≤tk.(2)
其中, Pi(t) 多项式中最高次项的幂,视为样条的阶数或次数(Order of spline),根据子区间 [ti−1,ti] 的区间长度是否一致分为均匀(Uniform)样条和非均匀(Non-uniform)样条。
满足了公式 (2) 的多项式有很多,为了保证曲线在 S 区间内具有据够的平滑度,一条n次样条,同时应具备处处连续且可微的性质:
P(j)i(ti)=P(j)i+1(ti);(3)
其中 i=1,…,k−1;j=0,…,n−1 。
2.三次样条曲线
2.1曲线条件
按照上述的定义,给定节点:
t:z:a=t0z0<t1z1<⋯⋯<tk−1zk−1<tkzk=b(4)
三次样条曲线满足三个条件:
- 在每段分段区间 [ti,ti+1],i=0,1,…,k−1 上, S(t)=Si(t) 都是一个三次多项式;
- 满足 S(ti)=zi,i=1,…,k−1 ;
- S(t) 的一阶导函数 S′(t) 和二阶导函数 S′′(t) 在区间 [a,b] 上都是连续的,从而曲线具有光滑性。
则三次样条的方程可以写为:
Si(t)=ai+bi(t−ti)+ci(t−ti)2+di(t−ti)3,(5)
其中, ai,bi,ci,di 分别代表 n 个未知系数。
- 曲线的连续性表示为:
Si(ti)=zi,(6)
Si(ti+1)=zi+1,(7)
其中 i=0,1,…,k−1 。
- 曲线微分连续性:
S′i(ti+1)=S′i+1(ti+1),(8)
S′′i(ti+1)=S′′i+1(ti+1),(9)
其中 i=0,1,…,k−2 。
- 曲线的导函数表达式:
S′i=bi+2ci(t−ti)+3di(t−ti)2,(10)
S′′i(x)=2ci+6di(t−ti),(11)
令区间长度 hi=ti+1−ti ,则有:
-
由公式 (6) ,可得: ai=zi ;
-
由公式 (7) ,可得: ai+bihi+cih2i+dih3i=zi+1 ;
-
由公式 (8) ,可得:
S′i(ti+1)=bi+2cihi+3dih2i ;
S′i+1(ti+1)=bi+1 ;
⇒bi+2cihi+3dih2i−bi+1=0 ; -
由公式 (9) ,可得:
S′′i(ti+1)=2ci+6dihi ;
S′′i+1(ti+1)=2ci+1 ;
⇒2ci+6dihi=2ci+1 ;设 mi=S′′i(xi)=2ci ,则:
A. mi+6dihi−mi+1=0⇒
di=mi+1−mi6hi ;B.将 ci,di 代入 zi+bihi+cih2i+dih3i=zi+1⇒
bi=zi+1−zihi−hi2mi−hi6(mi+1−mi) ;C.将 bi,ci,di 代入 bi+2cihi+3dih2i=bi+1⇒
himi+2(hi+hi+1)mi+1+hi+1mi+2=6[zi+2−zi+1hi+1−zi+1−zihi].(12)
2.2端点条件
在上述分析中,曲线段的两个端点 t0 和 tk 是不适用的,有一些常用的端点限制条件,这里只讲解自然边界。
在自然边界下,首尾两端的二阶导函数满足 S′′=0 ,即 m0=0 和 mk=0 。
3.三次样条插值类的实现
头文件
/**Cubic spline interpolation class.*
*/#ifndef CUBICSPLINEINTERPOLATION_H
#pragma once
#define CUBICSPLINEINTERPOLATION_H#include <iostream>
#include <vector>
#include <math.h>#include <opencv2/opencv.hpp>using namespace std;
using namespace cv;/* Cubic spline interpolation coefficients */
class CubicSplineCoeffs
{
public:CubicSplineCoeffs( const int &count ){a = std::vector<double>(count);b = std::vector<double>(count);c = std::vector<double>(count);d = std::vector<double>(count);}~CubicSplineCoeffs(){std::vector<double>().swap(a);std::vector<double>().swap(b);std::vector<double>().swap(c);std::vector<double>().swap(d);}public:std::vector<double> a, b, c, d;
};enum CubicSplineMode
{CUBIC_NATURAL, // NaturalCUBIC_CLAMPED, // TODO: ClampedCUBIC_NOT_A_KNOT // TODO: Not a knot
};enum SplineFilterMode
{CUBIC_WITHOUT_FILTER, // without filterCUBIC_MEDIAN_FILTER // median filter
};/* Cubic spline interpolation */
class CubicSplineInterpolation
{
public:CubicSplineInterpolation() {}~CubicSplineInterpolation() {}public:/*Calculate cubic spline coefficients.- node list x (input_x);- node list y (input_y);- output coefficients (cubicCoeffs);- ends mode (splineMode).*/void calCubicSplineCoeffs( std::vector<double> &input_x,std::vector<double> &input_y, CubicSplineCoeffs *&cubicCoeffs,CubicSplineMode splineMode = CUBIC_NATURAL,SplineFilterMode filterMode = CUBIC_MEDIAN_FILTER );/*Cubic spline interpolation for a list.- input coefficients (cubicCoeffs);- input node list x (input_x);- output node list x (output_x);- output node list y (output_y);- interpolation step (interStep).*/void cubicSplineInterpolation( CubicSplineCoeffs *&cubicCoeffs,std::vector<double> &input_x, std::vector<double> &output_x,std::vector<double> &output_y, const double interStep = 0.5 );/*Cubic spline interpolation for a value.- input coefficients (cubicCoeffs);- input a value(x);- output interpolation value(y);*/void cubicSplineInterpolation2( CubicSplineCoeffs *&cubicCoeffs,std::vector<double> input_x, double x, double &y );/*calculate tridiagonal matrices with Thomas Algorithm(TDMA) :example:| b1 c1 0 0 0 0 | |x1 | |d1 || a2 b2 c2 0 0 0 | |x2 | |d2 || 0 a3 b3 c3 0 0 | |x3 | = |d3 || ... ... | |...| |...|| 0 0 0 0 an bn | |xn | |dn |Ci = ci/bi , i=1; ci / (bi - Ci-1 * ai) , i = 2, 3, ... n-1;Di = di/bi , i=1; ( di - Di-1 * ai )/(bi - Ci-1 * ai) , i = 2, 3, ..., n-1xi = Di - Ci*xi+1 , i = n-1, n-2, 1;*/bool caltridiagonalMatrices( cv::Mat_<double> &input_a,cv::Mat_<double> &input_b, cv::Mat_<double> &input_c,cv::Mat_<double> &input_d, cv::Mat_<double> &output_x );/* Calculate the curve index interpolation belongs to */int calInterpolationIndex( double &pt, std::vector<double> &input_x );/* median filtering */void cubicMedianFilter( std::vector<double> &input, const int filterSize = 5 );double cubicSort( std::vector<double> &input );// double cubicNearestValue( std::vector );
};#endif // CUBICSPLINEINTERPOLATION_H
实现文件(cpp)
/** CubicSplineInterpolation.cpp*/#include "cubicsplineinterpolation.h"void CubicSplineInterpolation::calCubicSplineCoeffs(std::vector<double> &input_x,std::vector<double> &input_y,CubicSplineCoeffs *&cubicCoeffs,CubicSplineMode splineMode /* = CUBIC_NATURAL */,SplineFilterMode filterMode /*= CUBIC_MEDIAN_FILTER*/ )
{int sizeOfx = input_x.size();int sizeOfy = input_y.size();if ( sizeOfx != sizeOfy ){std::cout << "Data input error!" << std::endl <<"Location: CubicSplineInterpolation.cpp" <<" -> calCubicSplineCoeffs()" << std::endl;return;}/*hi*mi + 2*(hi + hi+1)*mi+1 + hi+1*mi+2= 6{ (yi+2 - yi+1)/hi+1 - (yi+1 - yi)/hi }so, ignore the both ends:| - - - 0 ... 0 | |m0 || h0 2(h0+h1) h1 0 ... 0 | |m1 || 0 h1 2(h1+h2) h2 0 ... | |m2 || ... ... 0 | |...|| 0 ... 0 h(n-2) 2(h(n-2)+h(n-1)) h(n-1) | | || 0 ... ... - | |mn |*/std::vector<double> copy_y = input_y;if ( filterMode == CUBIC_MEDIAN_FILTER ){cubicMedianFilter(copy_y, 5);}const int count = sizeOfx;const int count1 = sizeOfx - 1;const int count2 = sizeOfx - 2;const int count3 = sizeOfx - 3;cubicCoeffs = new CubicSplineCoeffs( count1 );std::vector<double> step_h( count1, 0.0 );// for m matrixcv::Mat_<double> m_a(1, count2, 0.0);cv::Mat_<double> m_b(1, count2, 0.0);cv::Mat_<double> m_c(1, count2, 0.0);cv::Mat_<double> m_d(1, count2, 0.0);cv::Mat_<double> m_part(1, count2, 0.0);cv::Mat_<double> m_all(1, count, 0.0);// initial step hifor ( int idx=0; idx < count1; idx ++ ){step_h[idx] = input_x[idx+1] - input_x[idx];}// initial coefficientsfor ( int idx=0; idx < count3; idx ++ ){m_a(idx) = step_h[idx];m_b(idx) = 2 * (step_h[idx] + step_h[idx+1]);m_c(idx) = step_h[idx+1];}// initial dfor ( int idx =0; idx < count3; idx ++ ){m_d(idx) = 6 * ((copy_y[idx+2] - copy_y[idx+1]) / step_h[idx+1] -(copy_y[idx+1] - copy_y[idx]) / step_h[idx] );}//cv::Mat_<double> matOfm( count2, )bool isSucceed = caltridiagonalMatrices(m_a, m_b, m_c, m_d, m_part);if ( !isSucceed ){std::cout<<"Calculate tridiagonal matrices failed!"<<std::endl<<"Location: CubicSplineInterpolation.cpp -> " <<"caltridiagonalMatrices()"<<std::endl;return;}if ( splineMode == CUBIC_NATURAL ){m_all(0) = 0.0;m_all(count1) = 0.0;for ( int i=1; i<count1; i++ ){m_all(i) = m_part(i-1);}for ( int i=0; i<count1; i++ ){cubicCoeffs->a[i] = copy_y[i];cubicCoeffs->b[i] = ( copy_y[i+1] - copy_y[i] ) / step_h[i] -step_h[i]*( 2*m_all(i) + m_all(i+1) ) / 6;cubicCoeffs->c[i] = m_all(i) / 2.0;cubicCoeffs->d[i] = ( m_all(i+1) - m_all(i) ) / ( 6.0 * step_h[i] );}}else{std::cout<<"Not define the interpolation mode!"<<std::endl;}
}void CubicSplineInterpolation::cubicSplineInterpolation(CubicSplineCoeffs *&cubicCoeffs,std::vector<double> &input_x,std::vector<double> &output_x,std::vector<double> &output_y,const double interStep )
{const int count = input_x.size();double low = input_x[0];double high = input_x[count-1];double interBegin = low;for ( ; interBegin < high; interBegin += interStep ){int index = calInterpolationIndex(interBegin, input_x);if ( index >= 0 ){double dertx = interBegin - input_x[index];double y = cubicCoeffs->a[index] + cubicCoeffs->b[index] * dertx +cubicCoeffs->c[index] * dertx * dertx +cubicCoeffs->d[index] * dertx * dertx * dertx;output_x.push_back(interBegin);output_y.push_back(y);}}
}void CubicSplineInterpolation::cubicSplineInterpolation2(CubicSplineCoeffs *&cubicCoeffs,std::vector<double> input_x, double x, double &y)
{const int count = input_x.size();double low = input_x[0];double high = input_x[count-1];if ( x<low || x>high ){std::cout<<"The interpolation value is out of range!"<<std::endl;}else{int index = calInterpolationIndex(x, input_x);if ( index >= 0 ){double dertx = x - input_x[index];y = cubicCoeffs->a[index] + cubicCoeffs->b[index] * dertx +cubicCoeffs->c[index] * dertx * dertx +cubicCoeffs->d[index] * dertx * dertx * dertx;}else{std::cout<<"Can't find the interpolation range!"<<std::endl;}}
}bool CubicSplineInterpolation::caltridiagonalMatrices(cv::Mat_<double> &input_a,cv::Mat_<double> &input_b,cv::Mat_<double> &input_c,cv::Mat_<double> &input_d,cv::Mat_<double> &output_x )
{int rows = input_a.rows;int cols = input_a.cols;if ( ( rows == 1 && cols > rows ) ||(cols == 1 && rows > cols ) ){const int count = ( rows > cols ? rows : cols ) - 1;output_x = cv::Mat_<double>::zeros(rows, cols);cv::Mat_<double> cCopy, dCopy;input_c.copyTo(cCopy);input_d.copyTo(dCopy);if ( input_b(0) != 0 ){cCopy(0) /= input_b(0);dCopy(0) /= input_b(0);}else{return false;}for ( int i=1; i < count; i++ ){double temp = input_b(i) - input_a(i) * cCopy(i-1);if ( temp == 0.0 ){return false;}cCopy(i) /= temp;dCopy(i) = ( dCopy(i) - dCopy(i-1)*input_a(i) ) / temp;}output_x(count) = dCopy(count);for ( int i=count-2; i > 0; i-- ){output_x(i) = dCopy(i) - cCopy(i)*output_x(i+1);}return true;}else{return false;}
}int CubicSplineInterpolation::calInterpolationIndex(double &pt, std::vector<double> &input_x )
{const int count = input_x.size()-1;int index = -1;for ( int i=0; i<count; i++ ){if ( pt > input_x[i] && pt <= input_x[i+1] ){index = i;return index;}}return index;
}void CubicSplineInterpolation::cubicMedianFilter(std::vector<double> &input, const int filterSize /* = 5 */ )
{const int count = input.size();for ( int i=filterSize/2; i<count-filterSize/2; i++ ){std::vector<double> temp(filterSize, 0.0);for ( int j=0; j<filterSize; j++ ){temp[j] = input[i+j - filterSize/2];}input[i] = cubicSort(temp);std::vector<double>().swap(temp);}for ( int i=0; i<filterSize/2; i++ ){std::vector<double> temp(filterSize, 0.0);for ( int j=0; j<filterSize; j++ ){temp[j] = input[j];}input[i] = cubicSort(temp);std::vector<double>().swap(temp);}for ( int i=count-filterSize/2; i<count; i++ ){std::vector<double> temp(filterSize, 0.0);for ( int j=0; j<filterSize; j++ ){temp[j] = input[j];}input[i] = cubicSort(temp);std::vector<double>().swap(temp);}
}double CubicSplineInterpolation::cubicSort( std::vector<double> &input )
{int iCount = input.size();for ( int j=0; j<iCount-1; j++ ){for ( int k=iCount-1; k>j; k-- ){if ( input[k-1] > input[k] ){double tp = input[k];input[k] = input[k-1];input[k-1] = tp;}}}return input[iCount/2];
}
相关文章:
插值)
Opencv实现的三次样条曲线(Cubic Spline)插值
1.样条曲线简介 样条曲线(Spline)本质是分段多项式实函数,在实数范围内有: S:[a,b]→R ,在区间 [a,b] 上包含 k 个子区间[ti−1,ti],且有: at0<t1<⋯<tk−1<tkb(1) 对应每一段区间 i 的存在多项式&…...
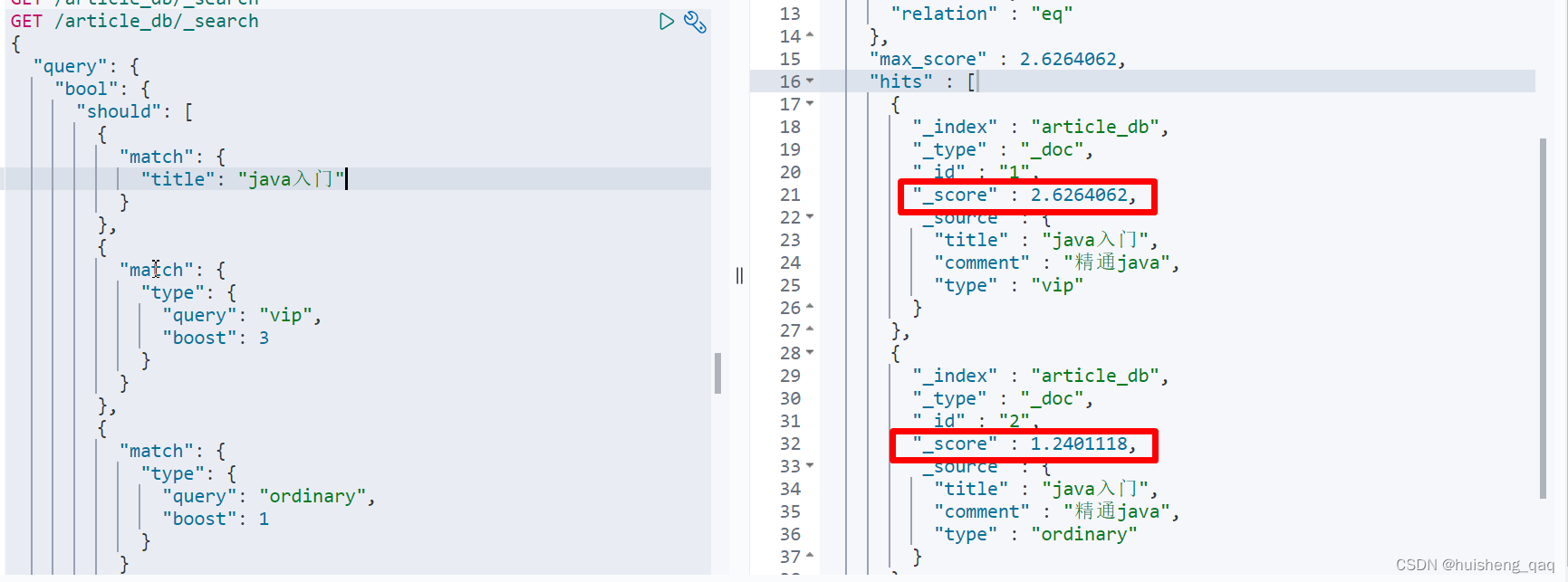
【ElasticSearch系列-03】ElasticSearch的高级句法查询Query DSL
ElasticSearch系列整体栏目 内容链接地址【一】ElasticSearch下载和安装https://zhenghuisheng.blog.csdn.net/article/details/129260827【二】ElasticSearch概念和基本操作https://blog.csdn.net/zhenghuishengq/article/details/134121631【二】ElasticSearch的高级查询Quer…...

【C++ 系列文章 -- 程序员考试 201811 下午场 C++ 专题 】
1.1 C 题目六 阅读下列说明和C代码,填写程序中的空(1) ~(5),将解答写入答题纸的对应栏内。 【说明】 以下C代码实现一个简单乐器系统,音乐类(Music)可以使用…...
javaEE -15( 13000字 JavaScript入门 - 2)
一:JavaScript(WebAPI) JS 分成三个大的部分 ECMAScript: 基础语法部分DOM API: 操作页面结构BOM API: 操作浏览器 WebAPI 就包含了 DOM BOM,这个是 W3C 组织规定的. (和制定 ECMAScript 标准的大佬们不是一伙人). 前面学的 JS 基础语法主要学的是 …...
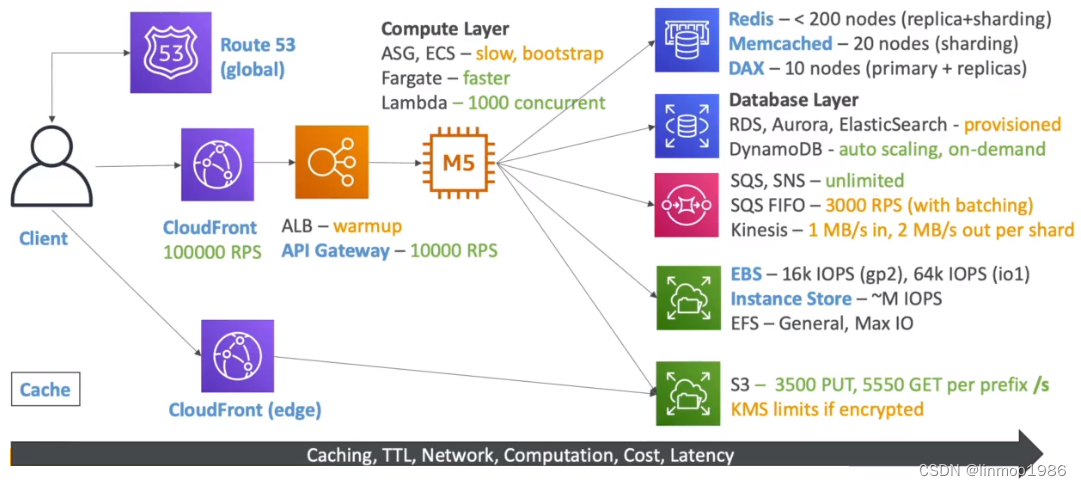
AWS SAP-C02教程11-解决方案
本章中,会根据一些常见场景的解决方案或者AWS的某一方面的总结,带你了解AWS各个组件之间的配合使用、如何在解决方案中选择组件以及如何避开其本身限制实现需求。 目录 1 处理高并发解决方案(Handing Extreme Rates)2 日志管理(AWS Managed Logs)3 部署解决方案(Deploy…...

ClickHouse Java多参UDF
一、环境版本 环境版本docker clickhouse22.3.10.22 docker pull clickhouse/clickhouse-server:22.3.10.22二、XML配置 2.1 配置文件 # 创建udf配置文件 vim /etc/clickhouse-server/demo_function.xml<functions><function><type>executable</type&…...
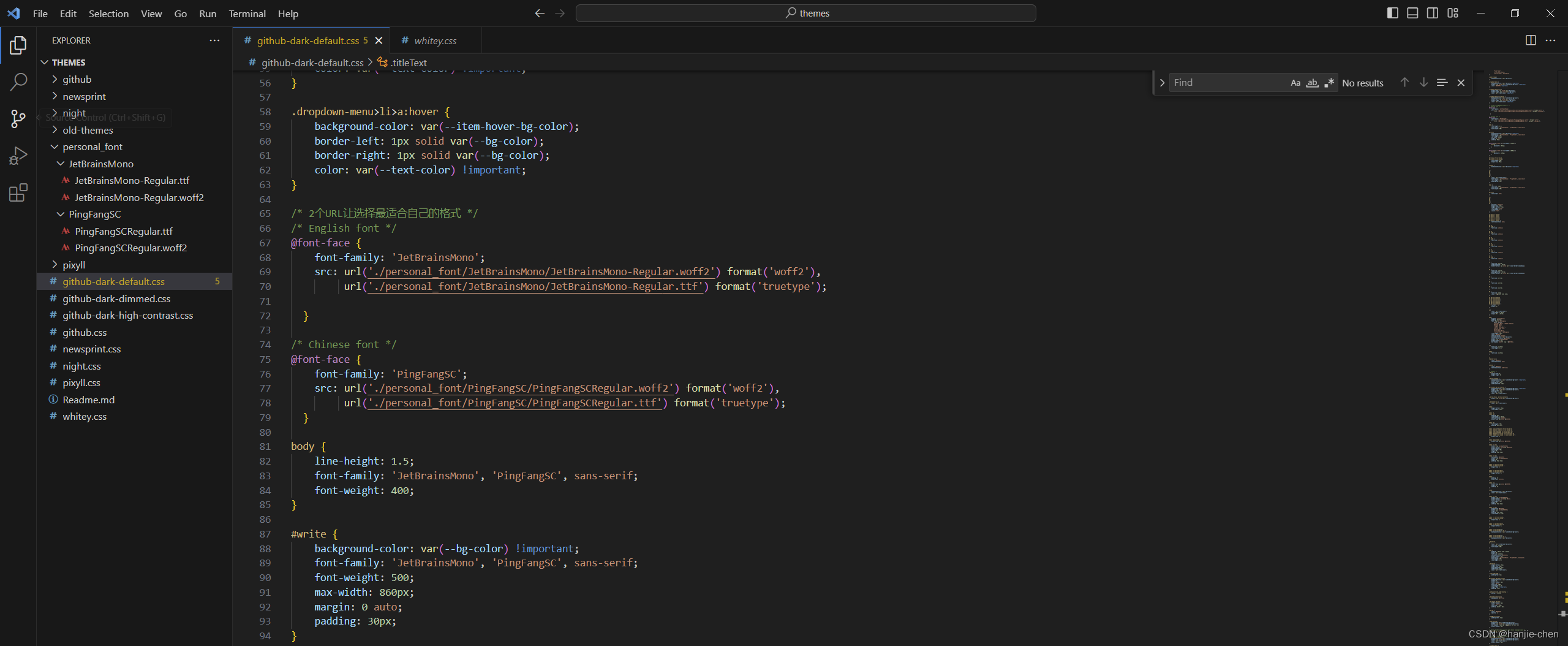
修改Typora默认微软雅黑字体
修改Typora字体 写在前面 我最近在折腾windows电脑,从macos转像windows不容易啊,因为键盘快捷键经常弄错,这篇文章就是修改Typora中字体显示的问题。 正文内容 我发现在windows中,字体非常的难看,微软雅黑也太丑了…...

ESP32网络开发实例-Web服务器显示LM35传感器数据
Web服务器显示LM35传感器数据 文章目录 Web服务器显示LM35传感器数据1、LM35介绍2、软件准备3、硬件准备4、代码实现4.1 LM35与ADS1115驱动4.2 Web服务器显示LM35传感器数据本文将介绍有关如何在ESP32的Web服务器中显示LM35 温度传感器数据。 1、LM35介绍 LM35 用于测量物体或…...

ATFX汇市:美联储11月利率决议再暂停加息,紧缩货币政策或已接近尾声
ATFX汇市:11月美联储利率决议结果在今日2:00公布,其中提到:美联储寻求以2%的速度实现最大的就业和通胀率,为了达成这些目标,美联储决定将联邦基金利率的目标区间维持在5.25%~5.5%;委员会将会考虑货币政策的…...
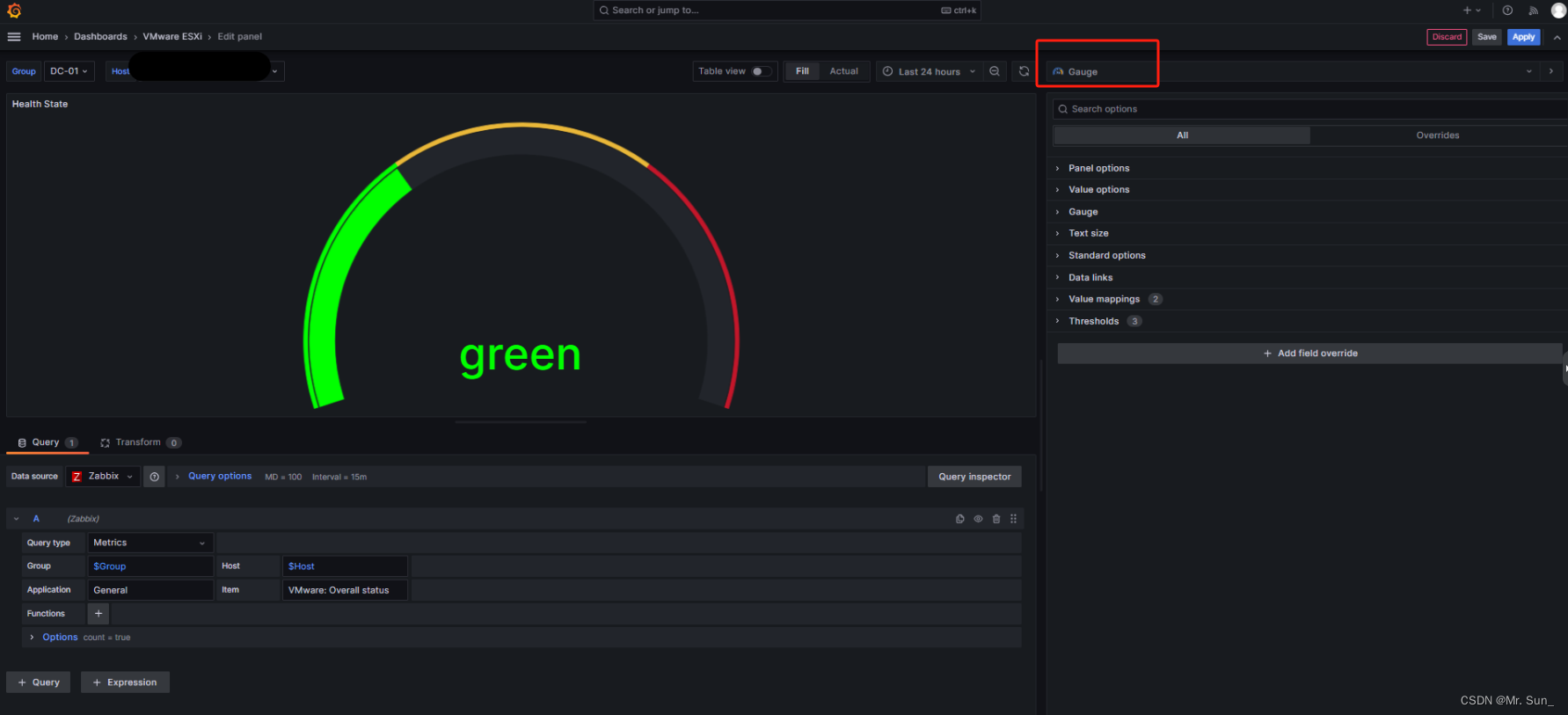
g.Grafana之Gauge的图形说明
直接上操作截图 1. 创建一个新的Dashboard 2.为Dashboard创建变量 【General】下的Name与Label的名称自定义 【Query options】 下的Group可以填写Zabbix内的所有组/.*/ , 然后通过Regex正则过滤需要的组名 3.设置Dashboard的图形 我使用文字来描述下这个图 1.我们在dash…...

MySQL笔记--Ubuntu安装MySQL并基于C++测试API
目录 1--安装MySQL 2--MySQL连接 3--代码案例 1--安装MySQL # 安装MySQL-Server sudo apt install mysql-server# 设置系统启动时自动开启 sudo systemctl start mysql # sudo systemctl enable mysql# 检查MySQL运行状态 sudo systemctl status mysql# 进入MySQL终端 sudo…...

与AI对话的艺术:如何优化Prompt以获得更好的响应反馈
前言 在当今数字化时代,人工智能系统已经成为我们生活的一部分。我们可以在智能助手、聊天机器人、搜索引擎等各种场合与AI进行对话。然而,要获得有益的回应,我们需要学会与AI进行有效的沟通,这就涉及到如何编写好的Prompt。 与…...
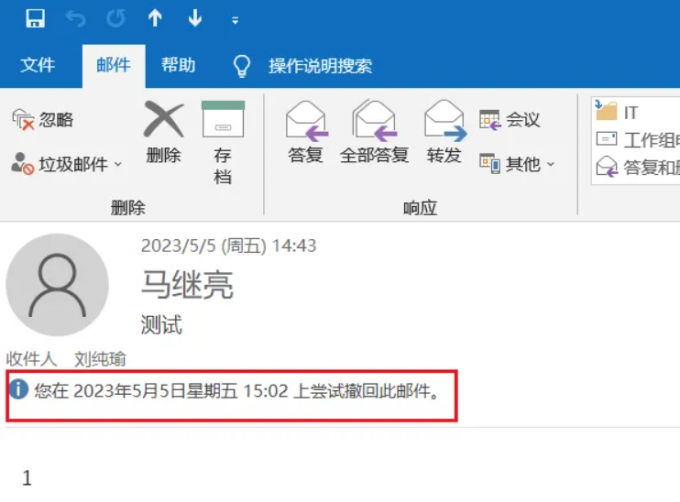
outlook是什么软件outlook邮箱撤回邮件方法
Outlook是微软公司开发的一款邮件客户端,也是Office办公套件的一部分。它可以与多个电子邮件服务提供商(如Outlook.com、Exchange、Gmail等)集成,用户可以使用Outlook来发送、接收和管理电子邮件、日历、联系人、任务等信息。本篇…...
电脑如何录制小视频
如果你想在你的电脑上录制视频分享给你的朋友或者亲人,无论你的电脑是win还是mac,都可以在本篇文章中找到电脑录制视频的详细教程。小编为你们整理了2种不同系统电脑的录制详细流程,继续阅读查看吧! 第一部分:windows…...

vue使用百度富文本
🔥博客主页: 破浪前进 🔖系列专栏: Vue、React、PHP ❤️感谢大家点赞👍收藏⭐评论✍️ 1、下载UEditor 链接已放到文章中了 2、上传到项目目录中 一般上传到public下,方便到时候打包进去,以免…...
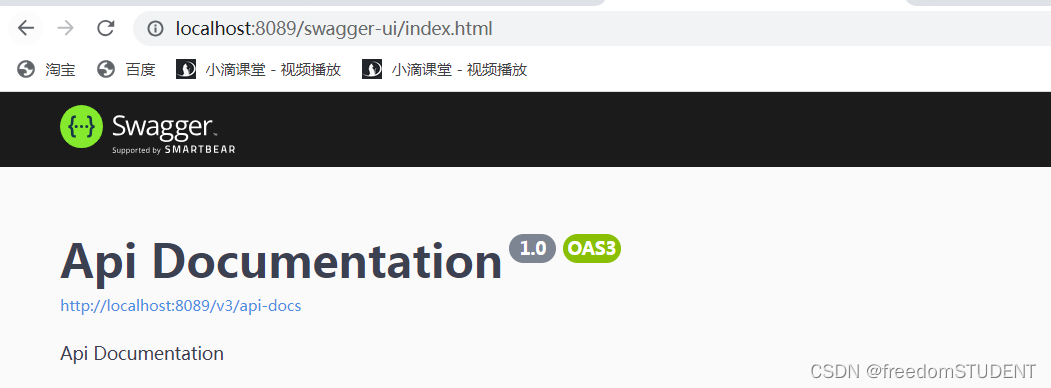
【Springboot】集成Swagger
引入依赖 <dependency><groupId>io.springfox</groupId><artifactId>springfox-boot-starter</artifactId><version>3.0.0</version> </dependency> 浏览器 启动项目后 在浏览器中输入地址 localhost:端口号/swagger-ui/ 使…...
[SpringCloud | Linux] CentOS7 部署 SpringCloud 微服务
目录 一、环境准备 1、工具准备 2、虚拟机环境 3、Docker 环境 二、项目准备 1、配置各个模块(微服务)的 Dockerfile 2、配置 docker-compose.yml 文件 3、Maven 打包 4、文件整合并传输 三、微服务部署 1、部署至 Docker 2、访问微服务 四…...

阿里面试:让代码不腐烂,DDD是怎么做的?
说在前面 在40岁老架构师 尼恩的读者交流群(50)中,最近有小伙伴拿到了一线互联网企业如阿里、滴滴、极兔、有赞、希音、百度、网易、美团的面试资格,遇到很多很重要的面试题: 谈谈你的高并发落地经验? 谈谈你对DDD的理解…...

NoSQL数据库使用场景以及架构介绍
文章目录 一. 什么是NoSQL?二. NoSQL分类三. NoSQL与关系数据库有什么区别四. NoSQL主要优势和缺点五. NoSQL体系框架 其它相关推荐: 系统架构之微服务架构 系统架构设计之微内核架构 鸿蒙操作系统架构 架构设计之大数据架构(Lambda架构、Kap…...

RFID系统提升物流信息管理效率应用解决方案
一、物流仓储管理方法 1、在仓库的进出口处安装RFID读写器,当粘贴RFID标签的电动叉车和货物进入装载区时,RFID读写器会自动检索并记录信息,当它们离开物流配送中心时,入口处的RFID读写器会读取标签信息,并生成出货单&…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
