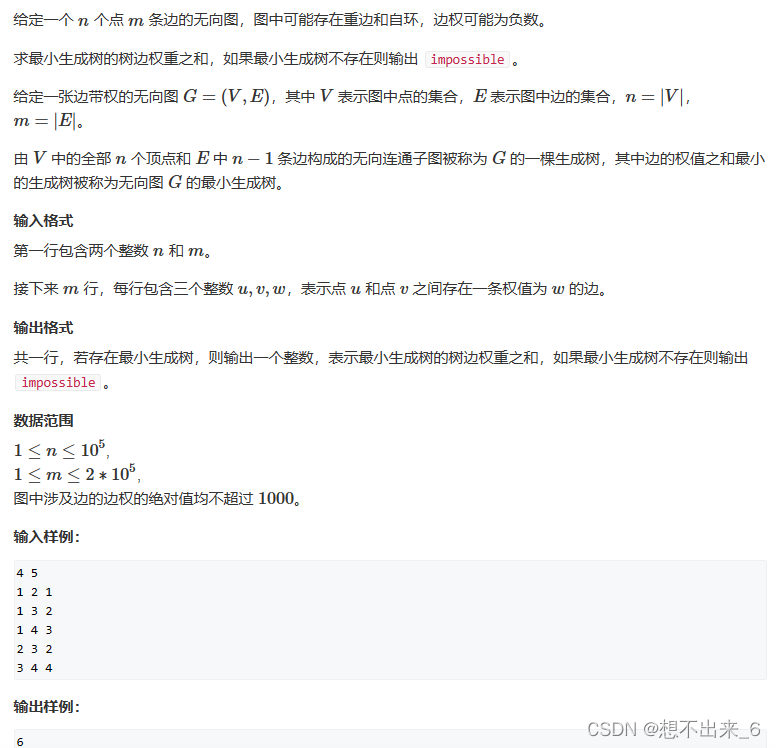
kruskal求最小生成树
算法思路:
将所有边按照权值的大小进行升序排序,然后从小到大一一判断。
如果这个边与之前选择的所有边不会组成回路,就选择这条边分;反之,舍去。
直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。
筛选出来的边和所有的顶点构成此连通网的最小生成树。
判断是否会产生回路的方法为:使用并查集。
在初始状态下给各个个顶点在不同的集合中。
遍历过程的每条边,判断这两个顶点的是否在一个集合中。
如果边上的这两个顶点在一个集合中,说明两个顶点已经连通,这条边不要。如果不在一个集合中,则要这条边。
//kruskal求最小生成树
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 2e5 + 9;struct Edge
{int a, b, w;bool operator< (const Edge& W) const{return w < W.w;}
} edges[N];int n, m, p[N], res, cnt;int find(int x)
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> n >> m;for (int i = 0; i < m; ++i){int a, b, w; cin >> a >> b >> w;edges[i] = { a, b, w };}//从小到大排序sort(edges, edges + m);//并查集数组初始化for (int i = 1; i <= n; ++i) p[i] = i;//如果这个边与之前选择的所有边不会组成回路,就选择这条边分;反之,舍去。//判断是否会产生回路的方法为:使用并查集。//每次将未加入的边加入到集合中去for (int i = 0; i < m; ++i){int a = edges[i].a, b = edges[i].b, w = edges[i].w;//不在一个集合里面a = find(a), b = find(b);if (a != b){res += w;cnt++;p[a] = b;//加入集合}}//如果集合中的边数小于n - 1,说明不存在最小生成树if (cnt < n - 1) cout << "impossible";else cout << res;return 0;
}
关于并查集可以看一下我写的这个篇文章: http://t.csdnimg.cn/ClmtA
相关文章:

kruskal求最小生成树
算法思路: 将所有边按照权值的大小进行升序排序,然后从小到大一一判断。 如果这个边与之前选择的所有边不会组成回路,就选择这条边分;反之,舍去。 直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。 筛选出来的边…...

876. 链表的中间结点
876. 链表的中间结点 算法 快慢指针 & 题目特征 需要对链表中的节点进行遍历,并且需要根据节点之间的相对位置或者距离进行操作 题目链接:https://leetcode.cn/problems/middle-of-the-linked-list/ 算法 快慢指针 & 题目特征 需要对链表中…...
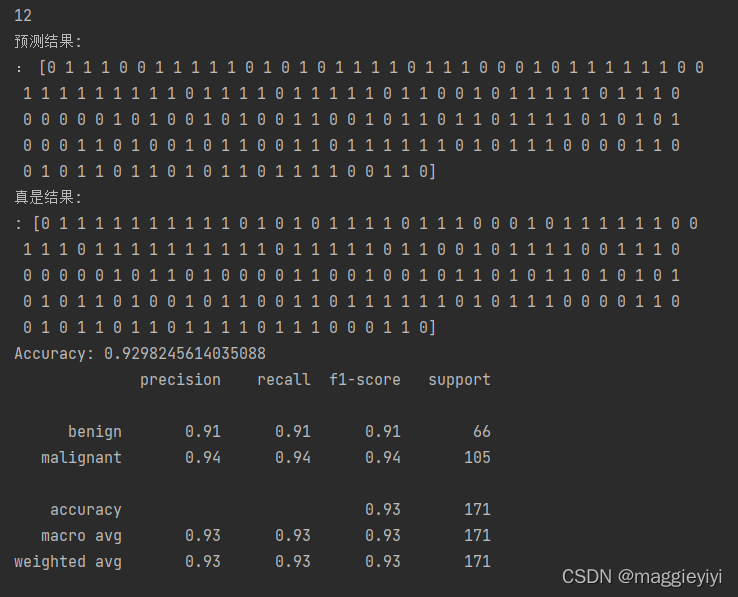
【机器学习】二、决策树
目录 一、决策树定义: 二、决策树特征选择 2.1 特征选择问题 2.2 信息增益 2.2.1 熵 2.2.2 信息增益 三、决策树的生成 3.1 ID3算法 3.1.1理论推导 3.1.2代码实现 3.2 C4.5 算法 3.2.1理论推导 3.2.2代码实现 四、决策树的剪枝 4.1 原理 4.2 算法思路:…...

低代码PAAS加速推进企业数字化转型
无论是“十四五”规划从国家层面提出的“加快数字化发展 建设数字中国”,还是后疫情时代企业自身的感受,数字化转型已成为必答题。当前 企业 业务场景化、线上趋势愈加明显,越来越多并发的数字化应用场景,而原有集中式架构扩展能力…...
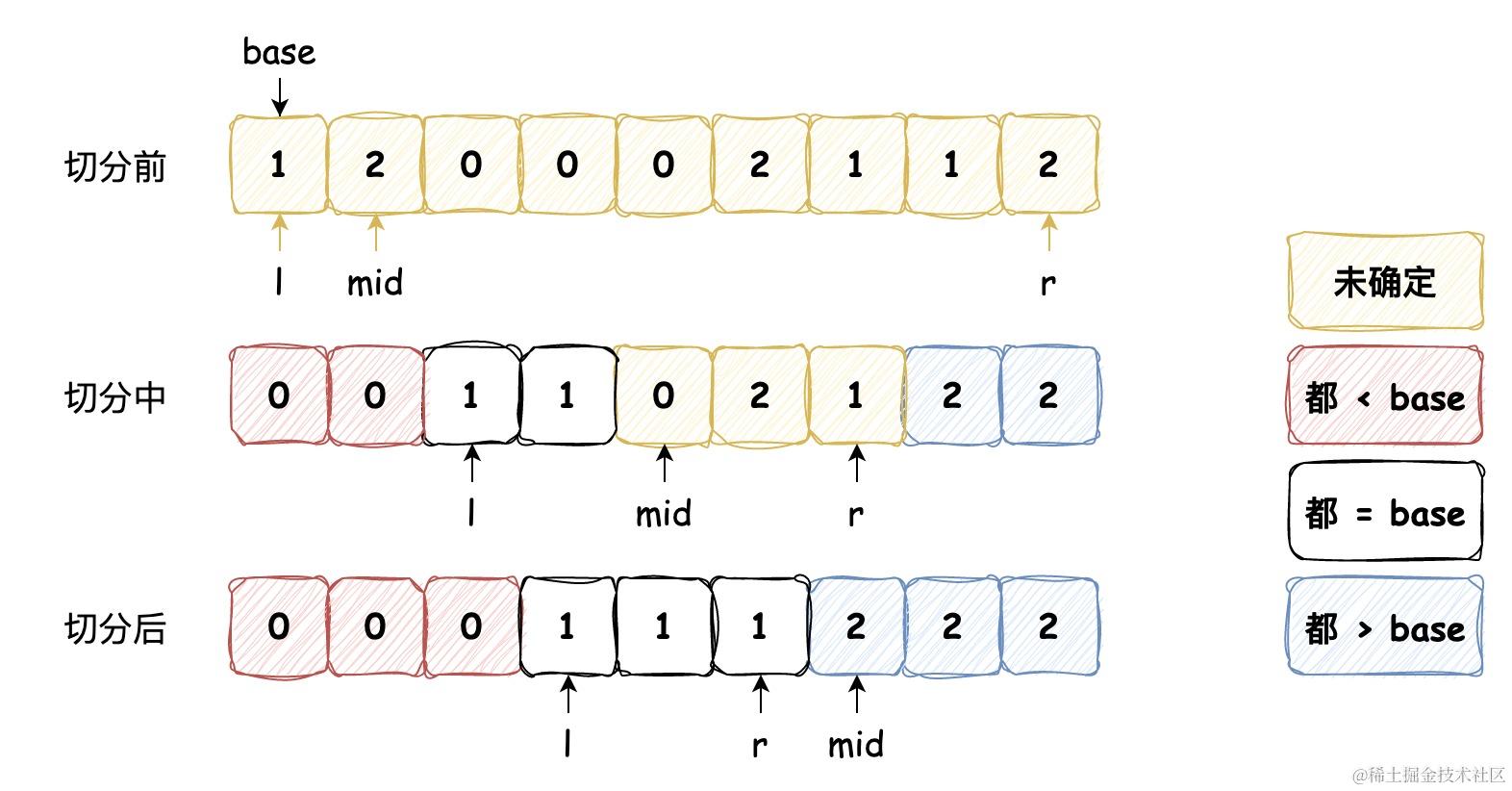
时间复杂度为 O(nlogn) 的排序算法
归并排序 归并排序遵循 分治 的思想:将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题,然后合并这些子问题的解来建立原问题的解,归并排序的步骤如下: 划分:分解待排序的 n 个元素…...
掌控你的Mac性能:System Dashboard Pro,一款专业的系统监视器
作为Mac用户,你是否曾经想要更好地了解你的电脑性能,以便优化其运行?是否想要实时监控系统状态,以便及时发现并解决问题?如果你有这样的需求,那么System Dashboard Pro就是你的不二之选。 System Dashboar…...

C++ Qt如何往Windows AppData目录写数据
在使用Qt开发客户端软件时,我们可以把程序相关信息保存到AppData目录, 下次启动时读取,就可以保存程序的状态,便于用户使用。 Windows AppData目录是Windows操作系统中的一个重要目录,主要用于存储应用程序的自定义设置、文件和数据。这个目录包含了许多与应用程序相关的配…...

xargs命令
xargs命令 xargs 命令是一个非常好用的 Linux 命令,它可以将管道或标准输入转换成命令行参数,并用这些参数来执行指定 的命令。默认情况下, xargs 命令会将输入按照空格、制表符、换行符等符号进行分隔,并将它们作为一组参数 传…...
【原创】java+swing+mysql无偿献血管理系统设计与实现
摘要: 无偿献血管理系统是为了实现无偿献血规范化、有序化、高效化的管理而设计的。本文主要介绍使用java语言开发一个基于C/S架构的无偿献血管理系统,提高无偿献血管理的工作效率。 功能分析: 系统主要提供给管理员、无偿献血人员&#x…...

C语言 Number 1 基本数据类型
数据类型的定义 c语言的数据分类基本类型整型浮点型float和double的精度和范围范围精度 枚举类型空类型派生类型派生的一般表达形式 注 c语言的数据分类 首先是针对C语言的数据类型做个整理 大致分为四个大类型 基本类型枚举类型空类型派生类型 那么根据以上四个大类型 我们…...

mac录屏快捷键指南,轻松录制屏幕内容!
“大家知道mac电脑有录屏快捷键吗,现在录屏不太方便,每次都花很多时间,要是有录屏快捷键,应该会快速很多,可是哪里都找不到,有人知道吗?帮帮我!” 苹果的mac电脑以其精美的设计和卓…...
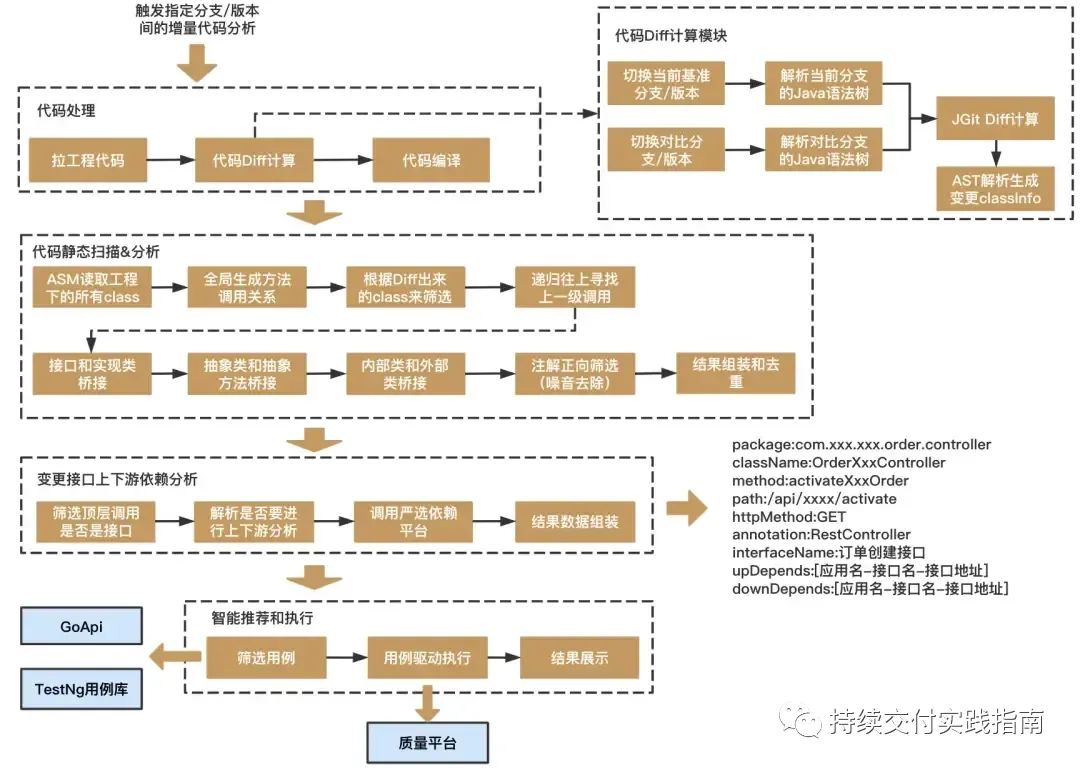
精准测试是个错误
如果你已经了解了精准测试在行业的主流做法,你可以跳过相关内容。 行业里对于精准测试的定义 在网上流传着一些精准测试的定义(如果你对这些定义不感冒,可直接跳到我个人的定义): 自网易陈逸青(2020&#x…...

算法通关村第四关|黄金挑战|表达式问题
1.计算器问题 给定一个内容为表达式的字符串,计算结果。 class Solution {public int calculate(String s) {Deque<Integer> stack new ArrayDeque<Integer>();char preSign ;int num 0;int n s.length();for (int i 0; i < n; i) {if (Chara…...
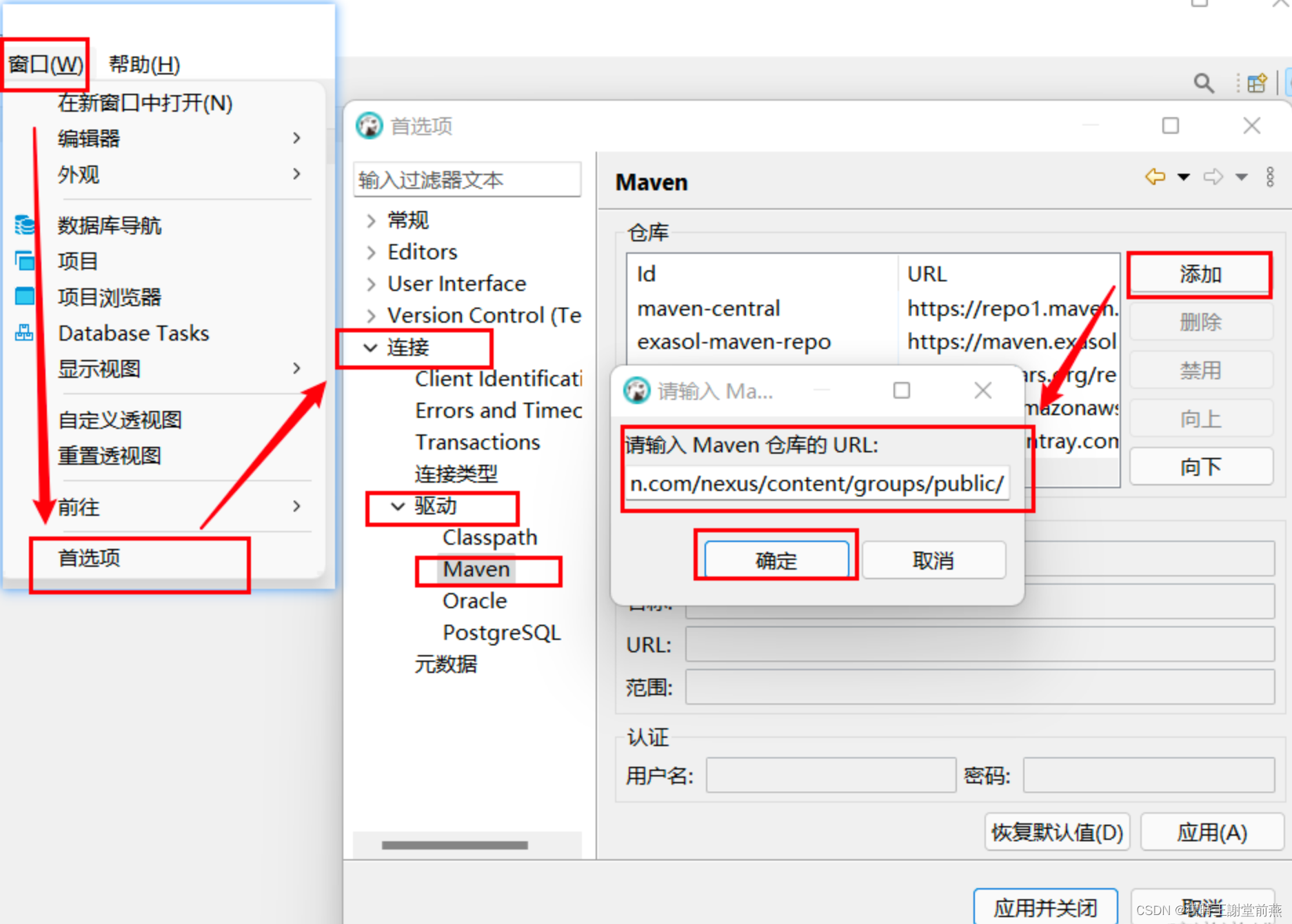
Mac安装DBeaver
目录 一、DBeaver Mac版软件简介 二、下载地址 三、DBeaver连接失败报错 3.1 问题描述 3.2 连接失败问题解决 一、DBeaver Mac版软件简介 DBeaver Mac版是一款专门为开发人员和数据库管理员设计的免费开源通用数据库工具。软件的易用性是它的宗旨,是经过精心设计…...

C++ 类 根据成员变量的指针获取类对象的指针
一.宏定义 实现方式有多种,原理是相同的 方式1: #define get_class_ptr(memberPtr,classType,memberName) \ ((classType*)((char*)(memberPtr)-(unsigned long)((ULONG_PTR)&((classType*)0)->member))) 方式2: #define get_cl…...
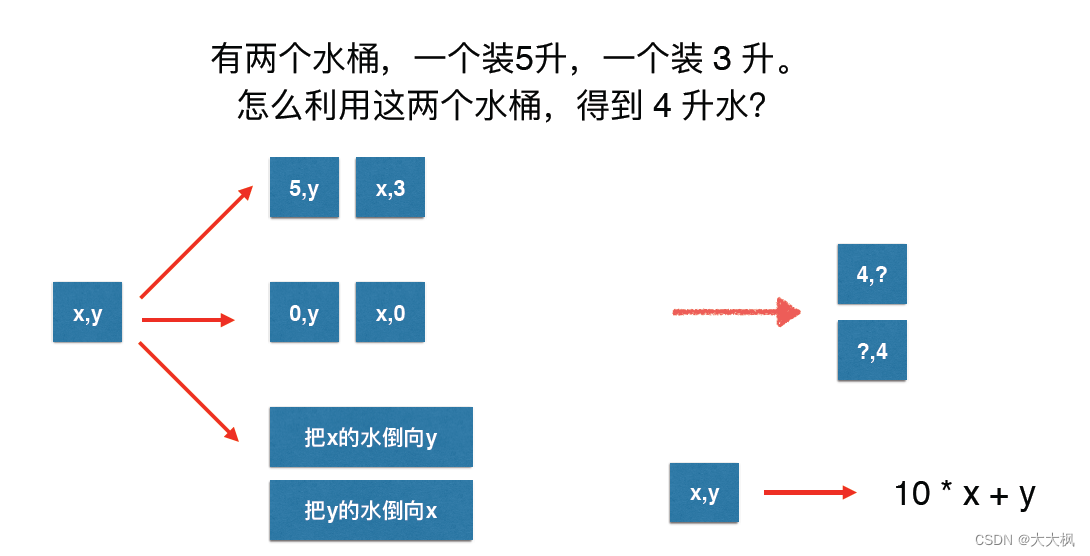
图论08-图的建模-状态的表达与理解 - 倒水问题为例
文章目录 状态的表达例题1题解1 终止条件:有一个数位为42 状态的改变:a表示十位数,b表示个位数3 其他设置 例题2 力扣773 滑动谜题JavaC 状态的表达 例题1 从初始的(x,y)状态,到最后变成(4,&am…...

sqlserver字符串拼接
本文主要介绍了sqlserver字符串拼接的实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值。 1. 概 在SQL语句中经常需要进行字符串拼接,以sqlserver,oracle,mysql三种数据库为例&#…...

MySQL-----事务
事务的概念 事务是一种机制,一个操作序列。包含了一组数据库的操作命令,所有的命令都是一个整体,向系统提交或者撤销的操作,要么都执行,要么都不执行。 是一个不可分割的单位 事务的ACID特点 ACID,是指在可…...

hive的安装配置笔记
1.上传hive安装包 2.解压 3.配置Hive(在一台机器上即可) mv hive-env.sh.template hive-env.sh 4.运行hive 发现内置默认的metastore存在问题(1.换执行路径后,原来的表不存在了。2.只能有一个用户访问同一个表) 5.配置mysql的meta…...

lamba stream处理集合
lamba stream处理集合 带拼接多字段分组List< Object> 转 Map<String,List< Object>> Map<String, List<ProfitAndLossMapping>> collect plMappingList.stream() .collect(Collectors.groupingBy(m -> m.getLosType() ":" m.…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...
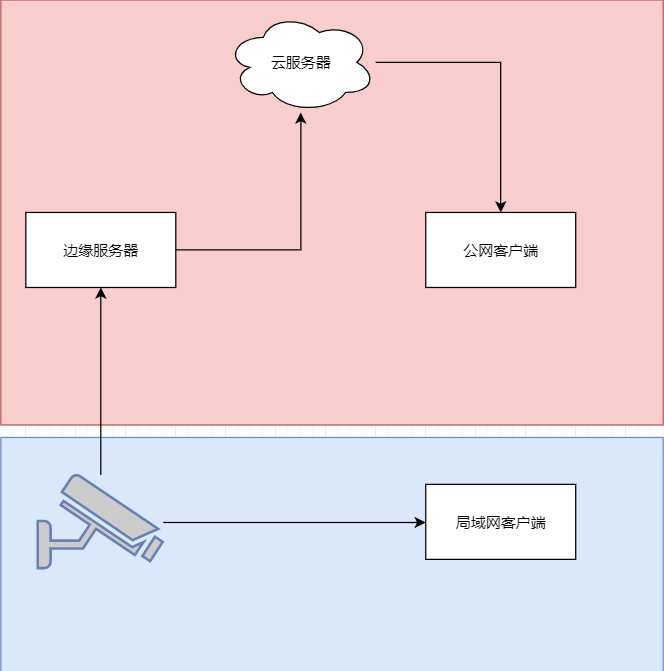
java 局域网 rtsp 取流 WebSocket 推送到前端显示 低延迟
众所周知 摄像头取流推流显示前端延迟大 传统方法是服务器取摄像头的rtsp流 然后客户端连服务器 中转多了,延迟一定不小。 假设相机没有专网 公网 1相机自带推流 直接推送到云服务器 然后客户端拉去 2相机只有rtsp ,边缘服务器拉流推送到云服务器 …...
