day52【子序列】300.最长递归子序列 674.最长连续递增序列 718.最长重复子数组
文章目录
- 300.最长递增子序列
- 674.最长连续递增序列
- 718.最长重复子数组
300.最长递增子序列
-
题目链接:力扣链接
-
讲解链接:代码随想录链接
-
题意:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:输入:nums = [10,9,2,5,3,7,101,18]输出:4解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。示例 2:输入:nums = [0,1,0,3,2,3]输出:4示例 3:输入:nums = [7,7,7,7,7,7,7]输出:1 -
思路:
- 当前下标i的递增子序列长度,和i之前的下标j的子序列长度有关系。
-
动规五部曲
dp[i]:表示i之前的包括i的,以nums[i]为尾的最长递增子序列的长度
递归公式:下标i的最长升序子序列长度等于下标j从0到i-1各个位置的最长升序子序列+1的最大值,也就是下标i之前的,即到i-1的最长升序子序列长度+下标i本身(+1)的长度。前提条件是,nums[i]>nums[j], 才会触发递归公式,这样才符合升序。dp[i] = Math.max(dp[i], dp[j]+1);
初始化:每个以nums[i]为结尾的子序列的长度最短都是它自己本身,也就是1,所以要把dp数组都初始化为1.
遍历顺序:内外两层遍历都是正序遍历即可
最后返回的结果:不是dp[nums.length-1],应为最后一个元素不一定是在最长子序列里面的,所以最后返回的结果应该去遍历每一个dp[i]找到最大的dp[i]来返回。
class Solution {public int lengthOfLIS(int[] nums) {int[] dp = new int[nums.length];//最小的结果就是1int result = 1;//把dp数组都初始化为1;Arrays.fill(dp, 1);for(int i = 0; i < dp.length; i++) {for(int j = 0; j < i; j++) {if(nums[i] > nums[j]) {dp[i] = Math.max(dp[j]+1, dp[i]);}}//找到最长的dp[i]作为结果。result = Math.max(result, dp[i]);}return result;}
}
674.最长连续递增序列
-
题目链接:力扣链接
-
讲解链接:代码随想录讲解
-
题意:给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:输入:nums = [1,3,5,4,7]输出:3解释:最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。 示例 2:输入:nums = [2,2,2,2,2]输出:1解释:最长连续递增序列是 [2], 长度为1。 -
思路:不同的是求连续递增的最长子序列的长度,这样的话i和i-1比较就行了,而不用引入j,让j在0到i-1中遍历得到最长的。
class Solution {public int findLengthOfLCIS(int[] nums) {//dp[i]代表以下标i为结尾的连续递增的子序列长度int[] dp = new int[nums.length];//初始化,dp[i]最少都应为1Arrays.fill(dp, 1);int res = 1;for(int i = 1; i < nums.length; i++) {//本题求连续增序列,所以就和i-1比较就行了,没必要和j比较,j是从0到i-1遍历。只要i比i-1大,那么最长的长度就得+1,如此一直遍历。 if(nums[i] > nums[i-1]) {dp[i] = Math.max(dp[i], dp[i-1]+1);}res = Math.max(res, dp[i]);}return res;}
}
718.最长重复子数组
-
题目链接:力扣链接
-
讲解链接:代码随想录讲解
-
题意:给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]输出:3解释:长度最长的公共子数组是 [3,2,1] 。示例 2:输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]输出:5 -
dp数组的含义
二维dp数组来表示两个数组的状态dp[i][j] 表示第一个数组到i-1为结尾,第二个数组到j-1为结尾的两个数组的最长重复子数组的长度。
为什么要以i-1和j-1为结尾,而不是以i和j为结尾呢?
因为如果是以i和j为结尾的话,在初始化时,就要对比nums1[0]和nums2的所有元素是否相等,以此来初始化nums[0][j]这一行,同理也要用相同的方法初始化nums[i][0]这一列。 -
递推公式
当nums1[i-1] == nums2[j-1]时(因为dp数组的定义是表示以i-1和j-1为结尾的,所以这里比较的是i-1和j-1的值相等,这是符合dp数组含义的),dp[i][j]需要加1,dp[i][j] = dp[i-1][j-1]+1,在[i-1][j-1]的基础上做加1,需要同时回退,然后在此基础上做+1的操作。 -
初始化
根据dp数组的定义,i和j为0时,dp数组表示以-1为结尾的,这是没有意义的,所以初始化为0,重复的长度如果有了就从0开始往上加,这样才正确。因为遍历时会把后面的初始值覆盖,所以其他初始值为多少都可以,但为方便统一设置为0.
dp[i][0] = 0
dp[0][j] = 0 -
遍历顺序
要遍历两个数组,两层for循环。遍历dp数组,找到最大值返回。
class Solution {public int findLength(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length+1][nums2.length+1];int res = 0;for(int i = 1; i <= nums1.length; i++) {for(int j = 1; j<= nums2.length; j++) {if(nums1[i-1] == nums2[j-1]) {dp[i][j] = Math.max(dp[i][j], dp[i-1][j-1]+1);}res = Math.max(res, dp[i][j]);}}return res;}
}
相关文章:

day52【子序列】300.最长递归子序列 674.最长连续递增序列 718.最长重复子数组
文章目录 300.最长递增子序列674.最长连续递增序列718.最长重复子数组 300.最长递增子序列 题目链接:力扣链接 讲解链接:代码随想录链接 题意:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而…...

计算机视觉 计算机视觉识别是什么?
计算机视觉识别(Computer Vision Recognition)是计算机科学和人工智能领域中的一个重要分支,它致力于使计算机系统能够模拟和理解人类视觉的过程,从而能够自动识别、分析和理解图像或视频中的内容。这一领域的发展旨在让计算机具备…...
Make.com实现多个APP应用的自动化的入门指南
Make.com是一款基于云的自动化平台,可帮助用户将多个应用程序连接在一起,并通过设置自动化流程来简化日常任务。Make.com提供丰富的API集成,支持连接各种流行的应用程序,包括社交媒体、电子商务、CRM等。 使用Make.com实现多个AP…...
的简介、原理、性能、实现步骤、案例应用之详细攻略)
LLMs之HFKR:HFKR(基于大语言模型实现异构知识融合的推荐算法)的简介、原理、性能、实现步骤、案例应用之详细攻略
LLMs之HFKR:HFKR(基于大语言模型实现异构知识融合的推荐算法)的简介、原理、性能、实现步骤、案例应用之详细攻略 目录 HFKR的简介 异构知识融合:一种基于LLM的个性化推荐新方法...

多模态 多引擎 超融合 新生态!2023亚信科技AntDB数据库8.0产品发布
9月20日,以“多模态 多引擎 超融合 新生态”为主题的亚信科技AntDB数据库8.0产品发布会成功举办,从技术和生态两个角度全方位展示了AntDB数据库第8次大型能力升级和生态建设成果。浙江移动、用友、麒麟软件、华录高诚、金云智联等行业伙伴及业界专家共同…...

elasticsearch无法访问9200端口
近期部署elasticsearch后,启动时发现一直报如下错误: curl: (7) Failed connect to localhost:9200; Connection refused 部署的版本为elasticsearch-7.13.2,排查原因是因为开启了ssl认证。 解决方法: 在/opt/software/elasticsearch-7.13.2/config下…...
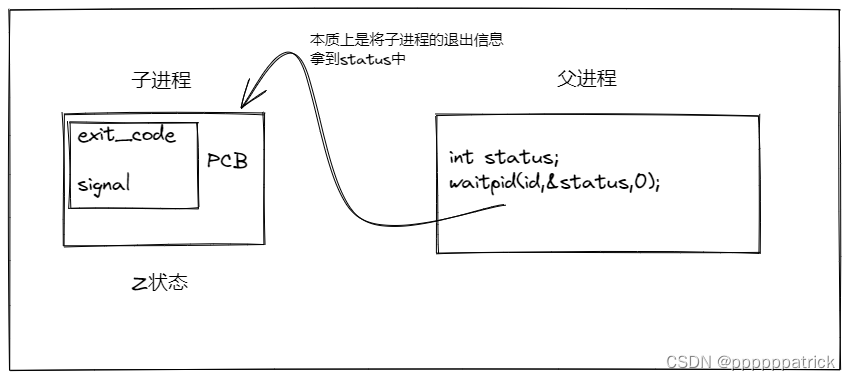
【Linux】进程等待
文章目录 进程等待进程等待必要性实验(见见猪跑)进程等待的方法wait方法waitpid**方法**宏的使用方法获取子进程status 阻塞VS非阻塞概念对比非阻塞有什么好处 具体代码实现进程的阻塞等待方式:进程的非阻塞等待方式:让父进程做其他任务 进程等待 进程等待必要性 之前讲过&am…...

电视「沉浮录」:跌出家电“三大件”?
【潮汐商业评论/原创】 “这年头谁还看电视,家里电视近一年都没打开过了,我明天就打算把它二手卖掉。”想到已落灰许久的电视机,Andy打开了二手平台。 “要不是这几年孩子网课多,我是真没考虑换新电视,家里用了8年的…...

前端实现调用打印机和小票打印(TSPL )功能
Ⅰ- 壹 - 使用需求 前端 的方式 点击这个按钮,直接让打印机打印我想要的东西 Ⅱ - 贰 - 小票打印 目前比较好的方式就是直接用 TSPL 标签打印指令集, 基础环境就不多说了,这个功能的实现就是利用usb发送指令,现在缺少个来让我们能够和usb沟通的工具,下面这就是推…...
串口通信(6)应用定时器中断+串口中断实现接收一串数据
本文为博主 日月同辉,与我共生,csdn原创首发。希望看完后能对你有所帮助,不足之处请指正!一起交流学习,共同进步! > 发布人:日月同辉,与我共生_单片机-CSDN博客 > 欢迎你为独创博主日月同…...
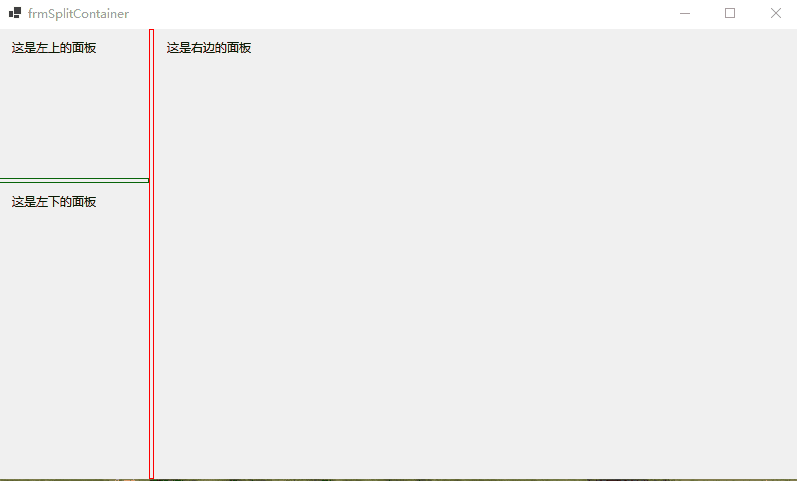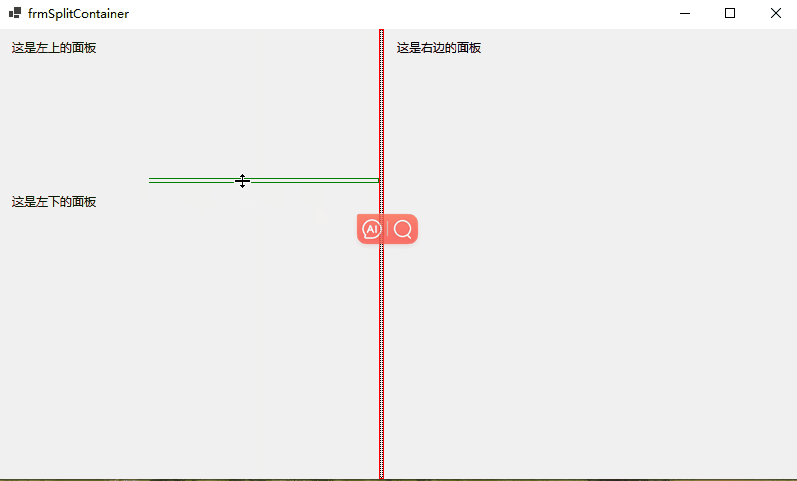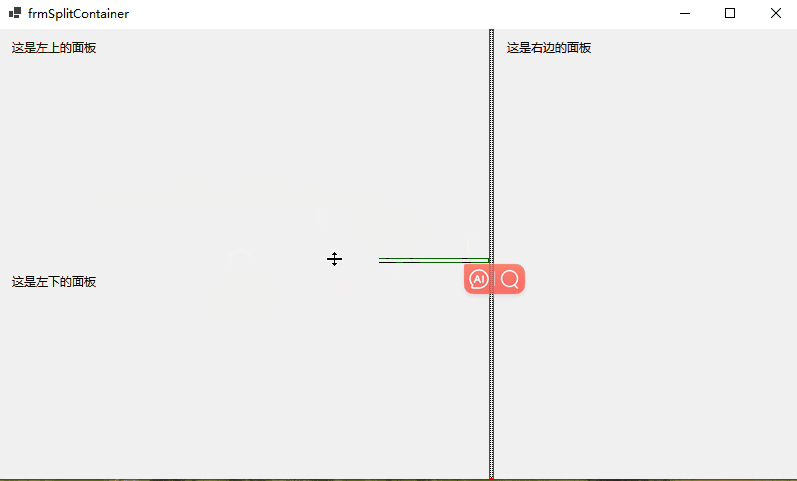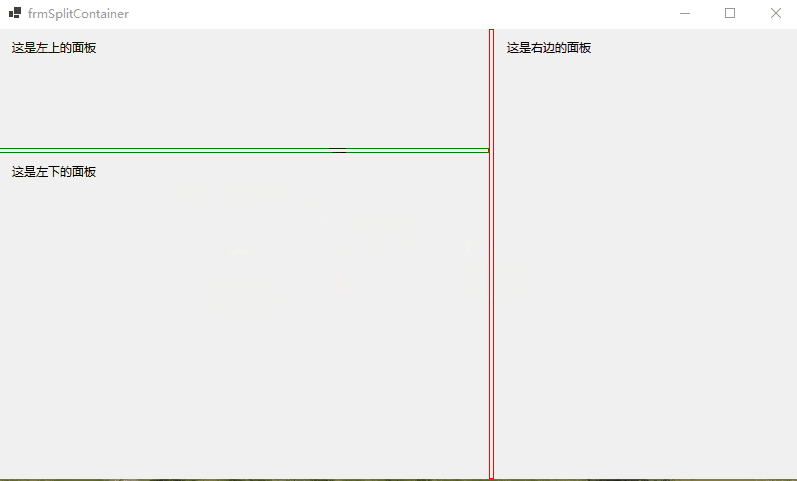
【WinForm详细教程六】WinForm中的GroupBox和Panel 、TabControl 、SplitContainer控件
文章目录 1.GroupBox和Panel2.TabControl3.SplitContainer 1.GroupBox和Panel GroupBox:是一个分组容器,提供一个框架将相关的控件组织在一起,它有标题、边框,但没有滚动条。 Panel:也是一个容器控件,用来…...

gradle与maven
Gradle 和 Maven 都是流行的构建工具,通常用于构建和管理 Java 和 Android 项目。它们都可以自动下载依赖库、编译代码、运行测试、打包和发布等。 以下是对 Gradle 和 Maven 的介绍: Gradle: Gradle 是一个基于 Groovy 和 Kotlin 的构建自…...
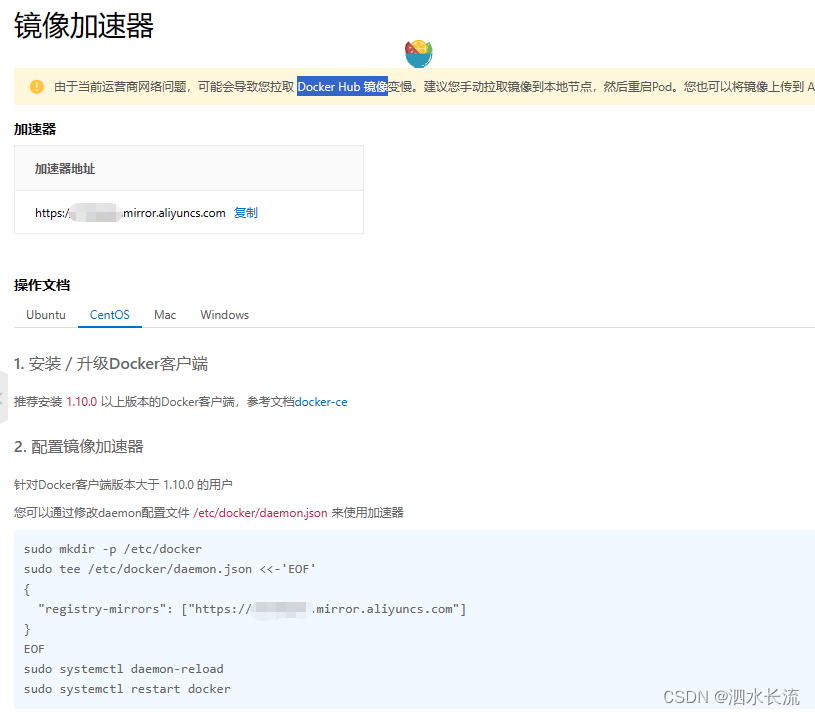
2.Docker基本架构简介与安装实战
1.认识Docker的基本架构 下面这张图是docker官网上的,介绍了整个Docker的基础架构,我们根据这张图来学习一下docker的涉及到的一些相关概念。 1.1 Docker的架构组成 Docker架构是由Client(客户端)、Docker Host(服务端)、Registry(远程仓库)组成。 …...

拓世法宝 | 数字经济崛起,美业如何抓住流量风口?
爱美之心,人皆有之。无论男女,都会很自然地对美好事物燃起兴致,跟高颜值相关的事物总能聚集注意力。例如直播平台里的美女网红收割流量赚得盆满钵满,面庞俊俏的年轻偶像吸引万千粉丝,还有“央视最美记者”王冰冰、“最…...
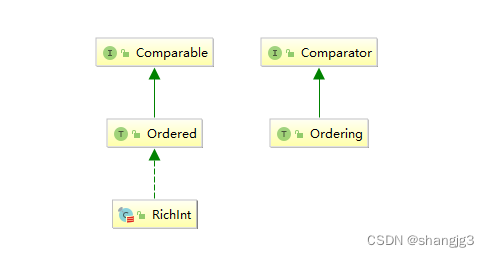
Scala 泛型编程
1. 泛型 Scala 支持类型参数化,使得我们能够编写泛型程序。 1.1 泛型类 Java 中使用 <> 符号来包含定义的类型参数,Scala 则使用 []。 class Pair[T, S](val first: T, val second: S) {override def toString: String first ":" sec…...

索引失效的场景有哪些?
虽然你这列上建了索引,查询条件也是索引列,但最终执行计划没有走它的索引。下面是引起这种问题的几个关键点。 列与列对比 某个表中,有两列(id和c_id)都建了单独索引,下面这种查询条件不会走索引 select…...

Java进阶04 final关键字、abstract抽象、interface接口、JDK8与JDK9中接口的区别、内部类和匿名类
文章目录 一、final关键字二、abstract关键字三、接口interface四、JDK8和JDK9中接口的区别五、内部类 一、final关键字 final可以修饰类、方法、变量 用final修饰类 表示此类不能被继承 用final修饰方法 表示方法不可以被重写 用final修饰变量 既可以修饰成员变量也可以修饰…...
Python的web自动化学习(五)Selenium的隐式等待(元素定位)
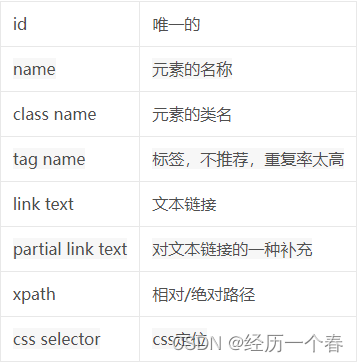
引言: WebDriver隐式等待是一种全局性的等待方式,它会在查找元素时设置一个固定的等待时间。当使用隐式等待时,WebDriver会在查找元素时等待一段时间,如果在等待时间内找到了元素,则立即执行下一步操作;如果…...
20231102从头开始配置cv180zb的编译环境(欢迎入坑,肯定还有很多问题等着你)
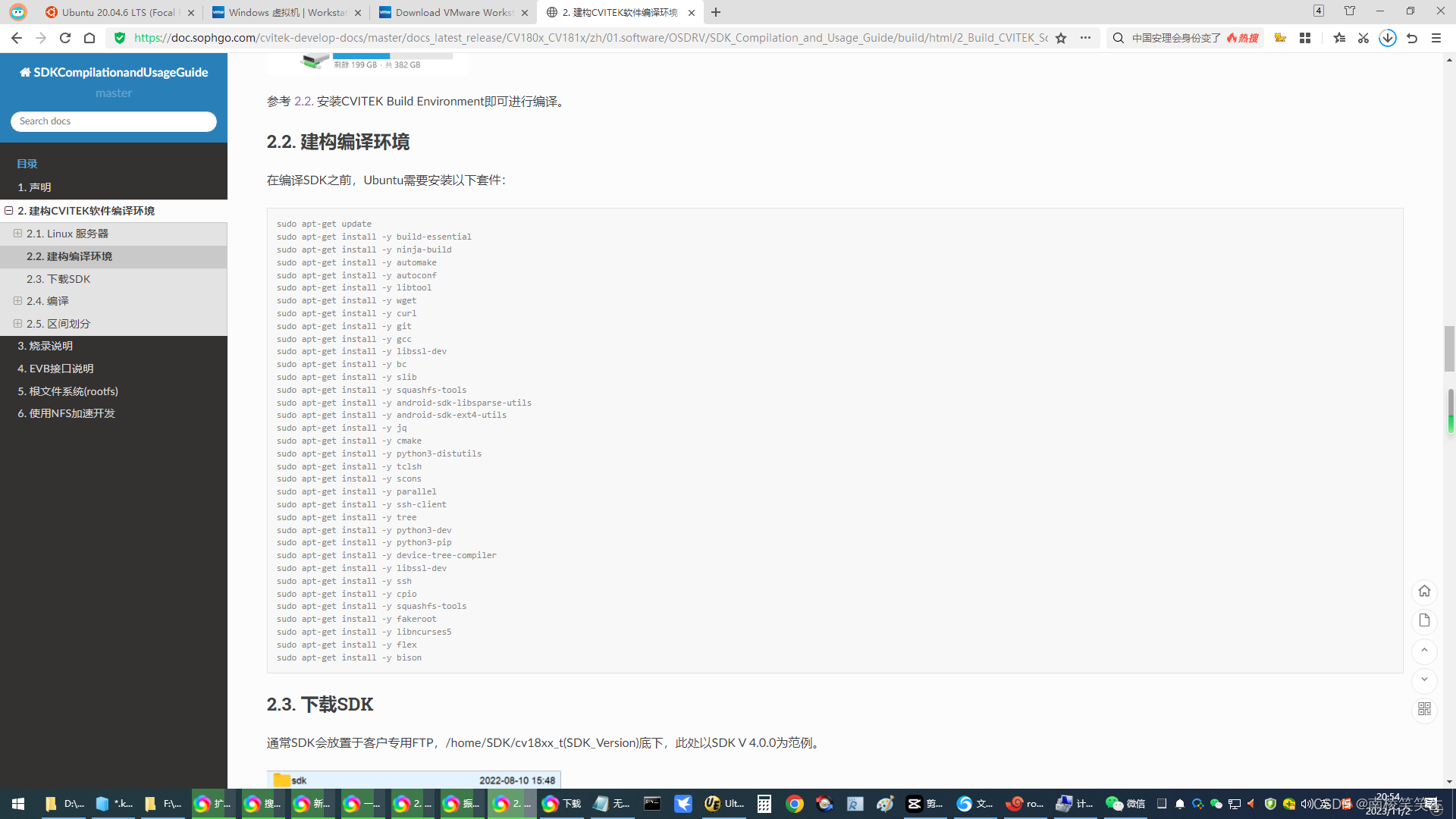
20231102从头开始配置cv180zb的编译环境(欢迎入坑,肯定还有很多问题等着你) 2023/11/2 11:31 (欢迎入坑,本篇只是针对官方的文档整理的!只装这些东西你肯定编译不过的,还有很多问题等着你呢&…...

CentOS 安装HTTP代理服务器 Squid
参考:大部分摘自此文,做了少部分修改 Squid 是一个功能全面的缓存代理服务器,它支持著名的网络协议像 HTTP,HTTPS,FTP 等等。将 Squid 放在网页服务器的前端,通过缓存重复请求,过滤网络流量等&…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
