筹码博弈K线长阳选股公式,穿越筹码密集区
普通K线是由最高价、开盘价、最低价、收盘价四个价格构成的,而博弈K线是以这个四个价格对应的获利盘构成K线,反映筹码的获利情况。把鼠标移动到K线上,停留在对应的价格,就可以在右侧的筹码分布图看到相应的获利盘数据。(如下图)
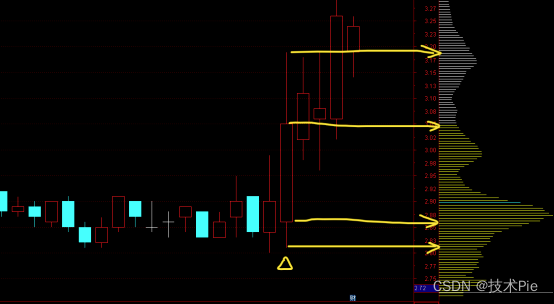
对于获利盘可以举一个例子,比如某一天开盘价的获利盘比例是30%,表示30%的筹码是获利的;收盘价的获利盘比例是70%,表示70%筹码是获利的。经过这一天的行情,从开盘到收盘,获利盘增加了40%,也就是说40%的筹码得到解套(从被套转为获利)。
通达信自带“博弈K线长度”指标,在通达信K线图界面,输入“CYQKL”,就可以加载到副图。这个指标用收盘价对应的获利盘比例减去开盘价对应的筹码比例,计算得到的就是解套筹码比例。
博弈K线长度指标公式:
KL:100*(WINNER(CLOSE)-WINNER(OPEN));
不过博弈K线长度指标看起来不是很直观,类似于普通K线的博弈K线通达信中没有,需要自己编写。
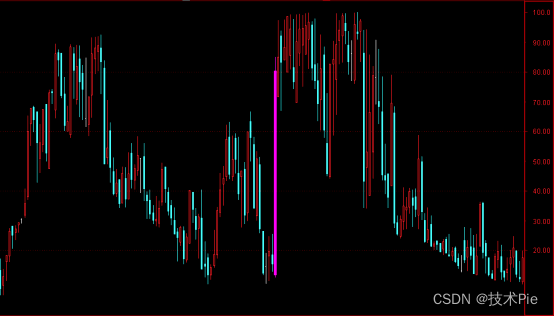
一、筹码博弈K线副图指标公式
思路:首先计算高、开、低、收四个价格对应的获利盘比例,得到结果之后,用DRAWKLINE绘制出博弈K线。然后用收盘价对应的获利盘比例BYC减去开盘价对应的获利盘比例BYO,得到解套的筹码比例。对于解套筹码比例大于50%的博弈K线,显示为洋红色。WINNER函数取值范围是0-1,乘以100转化为百分比,因此指标的取值范围是0-100。
BYH:=WINNER(H)*100;{最高价对应的获利盘比例}
BYO:=WINNER(O)*100;{开盘价对应的获利盘比例}
BYL:=WINNER(L)*100;{最低价对应的获利盘比例}
BYC:=WINNER(C)*100;{收盘价对应的获利盘比例}
KL:=BYC-BYO;{解套筹码比例}
STICKLINE(KL>50,BYH,BYL,0,1),COLORMAGENTA;
STICKLINE(KL>50,BYC,BYO,3,0),COLORMAGENTA;{解套筹码比例大于50%,洋红色}
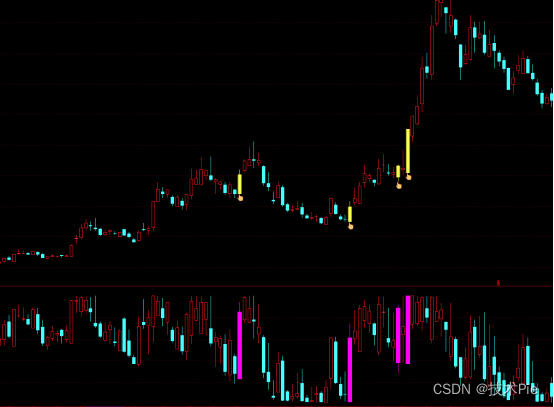
二、博弈K线长阳主图指标公式
思路:把博弈K线长阳显示到对应的K线主图。
BYH:=WINNER(H)*100;
BYO:=WINNER(O)*100;
BYL:=WINNER(L)*100;
BYC:=WINNER(C)*100;
KL:=BYC-BYO;
XG:=KL>50;
STICKLINE(XG,H,L,0,1),COLORYELLOW;
STICKLINE(XG,C,O,3,0),COLOR117777;
STICKLINE(XG,C,O,2.5,0),COLOR119999;
STICKLINE(XG,C,O,2,0),COLOR11BBBB;
STICKLINE(XG,C,O,1.5,0),COLOR11DDDD;
STICKLINE(XG,C,O,1,0),COLOR44FFFF;
DRAWICON(XG,L,11);
三、博弈K线长阳选股公式
BYH:=WINNER(H)*100;
BYO:=WINNER(O)*100;
BYL:=WINNER(L)*100;
BYC:=WINNER(C)*100;
KL:=BYC-BYO;
XG:KL>50;
最后说明一下,本文的推论(比如解套筹码等)建立在筹码分布理论模型上的,理论模型并不一定能反映所有的真实情况,但是可以给我们提供一个分析框架。
相关阅读:
筹码集中度计算公式,解决了结果不同的问题
超跌反弹选股公式,使用筹码函数WINNER
关注技术Pie,学习更多通达信指标公式编写知识。版权所有,转载请注明出处。
友情提醒:本文仅供学习交流技术指标公式,不构成任何投资建议。投资有风险,入市需谨慎。
相关文章:

筹码博弈K线长阳选股公式,穿越筹码密集区
普通K线是由最高价、开盘价、最低价、收盘价四个价格构成的,而博弈K线是以这个四个价格对应的获利盘构成K线,反映筹码的获利情况。把鼠标移动到K线上,停留在对应的价格,就可以在右侧的筹码分布图看到相应的获利盘数据。࿰…...
)
微服务设计模式-架构真题(六十八)
UNIX的源代码控制工具(Source Code control System,SCCS)是项目开发中常用的()。 源代码静态分析工具文档分析工具版本控制工具再工程工具 答案:C 解析: SCCS是版本控制工具 网闸的描述错误的是()。 双…...

LeetCode----52. N 皇后 II
题目 n 皇后问题 研究的是如何将 n 个皇后放置在 n n 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。 示例 1: 输入:n = 4 输出:2 解释:如上图所示,4 皇后问题存在两个不同的解法。 示例 2: 输入:n = …...
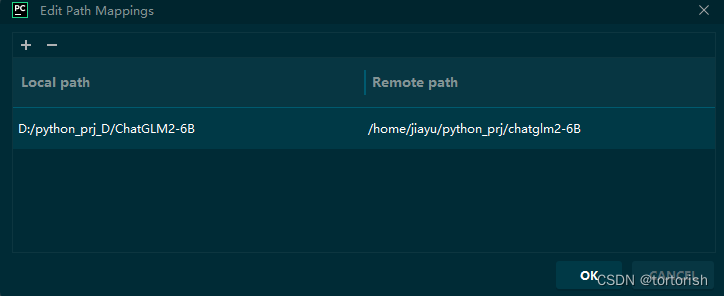
解决pycharm中,远程服务器上文件找不到的问题
一、问题描述 pycharm中,当我们连接到远程服务器上时。编译器中出现报错问题: cant open file /tmp/OV2IRamaar/test.py: [Errno 2] No such file or directory 第二节是原理解释,第三节是解决方法。 二、原理解释 实际上这是由于我们没有设置…...

虹科荣誉 | 喜讯!虹科成功入选“广州首届百家新锐企业”!!
文章来源:虹科品牌部 阅读原文:虹科荣誉 | 喜讯!虹科成功入选“广州首届百家新锐企业”!! 近日,由中共广州市委统战部、广州市工商业联合会、广州市工业和信息化局、广州市人民政府国有资产监督管理委员会…...

如何利用Jmeter从0到1做一次完整的压测?这2个步骤很关键!
压测,在很多项目中都有应用,是测试小伙伴必备的一项基本技能,刚好最近接手了一个小游戏的压测任务,一轮压测下来,颇有收获,赶紧记录下来,与大家分享一下,希望大家能少踩坑。 一、压…...
_2023)
基于STM32+微信小程序设计的智能门锁(4种开锁方式)_2023
一、项目介绍 1.1 项目背景 随着智能家居的普及,智能门锁作为一个非常重要的组成部分,受到了人们越来越多的关注。传统的机械锁门禁已经不能满足人们对于门锁安全、便捷性和智能化的需求,因此市场对于智能门锁的需求不断增加。而随着技术的发展,基于单片机的智能门锁已经…...

享受户外的美好时光:花园吊椅的魅力
拥有舒适的花园吊椅,就像在家中创造了一个度假天堂。这些轻松摇摆的座位为您提供了一个完美的地方,既能舒适躺卧,又能让您在家中的花园或庭院中感受到度假的氛围。度过美好时光的吊椅,将成为家庭花园的一大亮点,为您带…...

游戏中找不到d3dx9_43.dll怎么办,教你快速解决方法
在计算机的世界里,我们经常会遇到一些让人头疼的问题。比如,有一天,小明正在玩他最喜欢的游戏,突然弹出了一个错误提示:“由于找不到d3dx9_43.dll,无法继续执行代码”。小明感到非常困惑,不知道这是什么意思…...

蓝桥杯:买不到的数目
对于两个互质的正整数 n , m n,m n,m,请找出来不能被 n n n和 m m m组成的最大数 X X X 例如:对于4,7那么 X X X17,因为对于大于17的任一数都可由4和7组成。 重新翻译题目: 对于任一大于 X X X的正整数 Y Y Y满足 Y a n b m Y a \times nb \times m …...
Nginx简介,Nginx搭载负载均衡以及Nginx部署前端项目
目录 一. Nginx简介 Nginx的优点 二. Nginx搭载负载均衡 2.1 Nginx安装 2.1.1 安装依赖 2.1.2 解压nginx安装包 2.1.3 安装nginx 2.1.4 启动nginx服务 2.2 tomcat负载均衡 2.3 Nginx配置 三. Nginx前端部署 一. Nginx简介 NGINX(读作:engi…...
QT5.15.2搭建Android编译环境及使用模拟器调试(全)
一、安装QT5.15.2 地址:下载 我电脑的windows的,所以选windows 由于官方安装过程非常非常慢,一定要跟着步骤来安装,不然慢到怀疑人生 1)打开"命令提示符"(开始 -> Windows 系统 -> 命令…...

npm install报 ERESOLVE unable to resolve dependency tree
三四年前的一个项目,打开,npm install 一下,结果报 ERESOLVE unable to resolve dependency tree。 以前install都一切顺利,现在就不行,那很大的可能是npm的版本不同。 PS D:\workSpace\code\*-admin-ui-master> n…...

CentOS 7上创建Python 3虚拟环境
在CentOS 7上创建Python 3虚拟环境可以使用virtualenv包。以下是创建Python 3虚拟环境的步骤: 确保已经安装了Python 3和pip。可以通过在终端中运行以下命令来检查它们是否已安装: python3 --version pip3 --version如果未安装,请使用以下…...
B端设计必看的9个开源组件库,值得收藏!
如果你想开发一款To B Web端产品,如何选择令人眼花缭乱的开源组件库?行业团队常用的B端开源组件库是什么?今天,我们将为您带来入门级开源组件库的介绍。你可以先有一个大致的了解,希望能对你有所帮助。未来,…...

王坚院士:云计算与 GPT 的关系,就是电和电动机的关系
无论是行业,还是阿里,都身处巨变时。已经年过六十的王坚院士,重回阿里,重回大众视野,今年以来,在多个场合都能够看到他的身影。 而每一次他的分享,都值得我们细细品味。 以下为王坚院士在 202…...
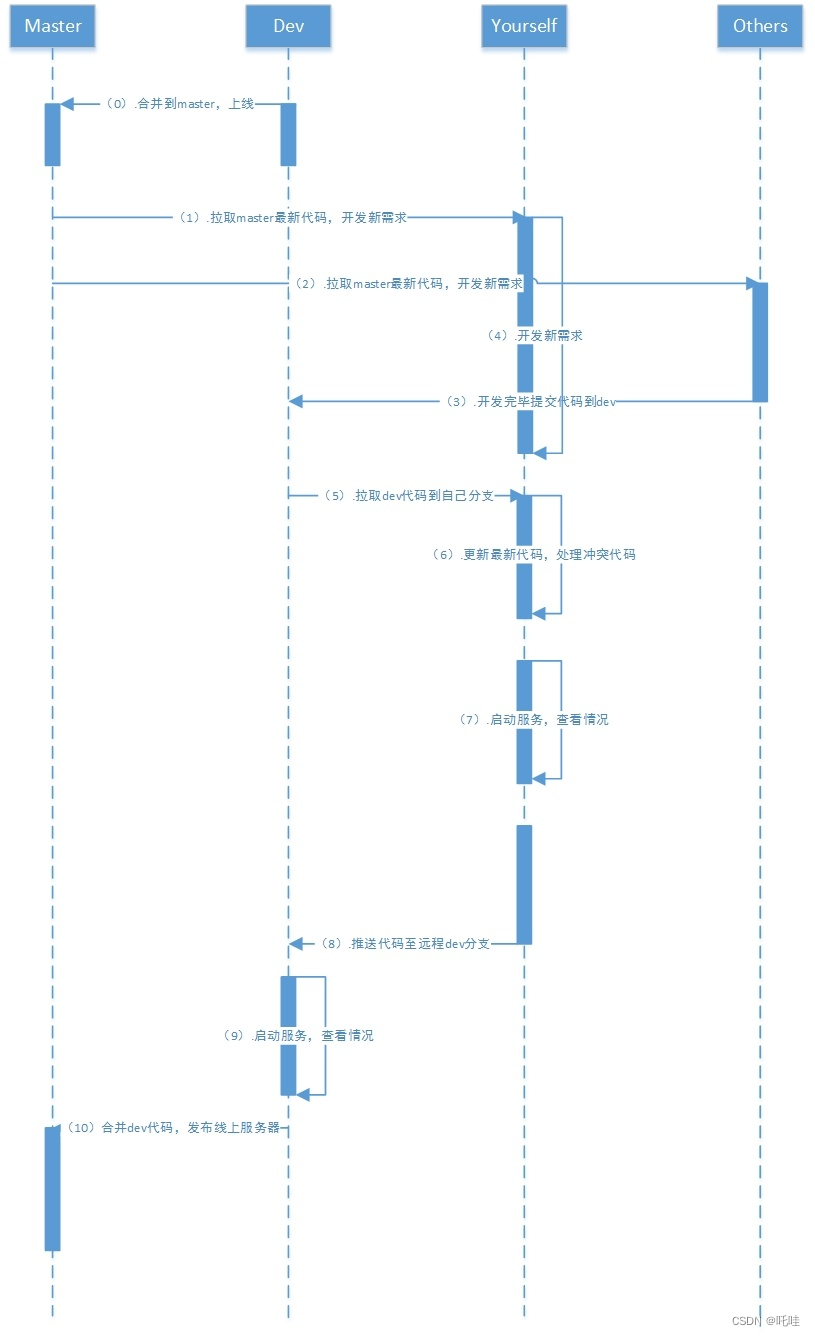
Git代码合并流程规范
...

编译cef114.2 with h264
按照下面网页要求安装VS和SDK https://bitbucket.org/chromiumembedded/cef/wiki/BranchesAndBuilding.md#markdown-header-development Win 10 deployment, Win 10 build system w/ VS2022 17.5, Win 10.0.22621 SDK, Ninja rem 配置winsock科学上网 netsh winhttp set prox…...
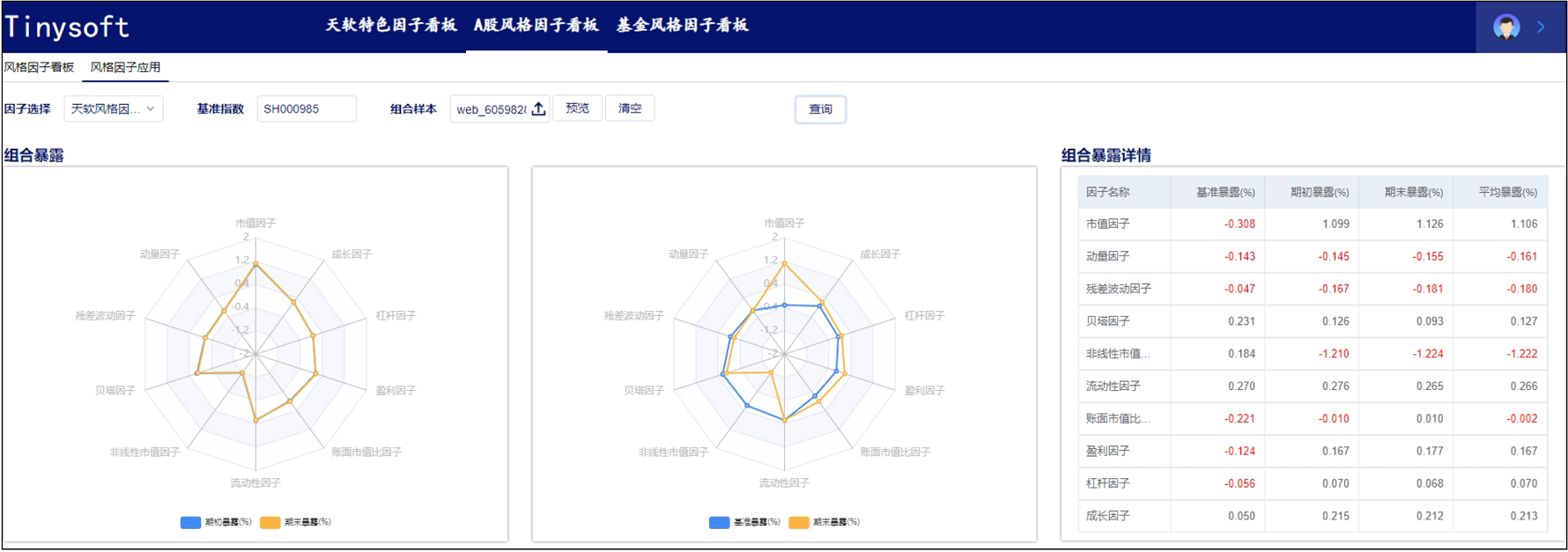
A股风格因子看板 (2023.11第01期)
该因子看板跟踪A股风格因子,该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子,用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第01期,指数组合数据截止日2023-10-31,要点如下 近1年A股风格因子收益走…...

Session+Cookie实现登录认证
使用 Session 和 Cookie 实现登录认证的流程通常包括以下步骤: 1. 登录认证流程 用户登录: 用户在登录页面输入用户名和密码。 服务器验证用户的凭证(用户名和密码)是否正确。 创建会话(Session)…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...

可下载旧版app屏蔽更新的app市场
软件介绍 手机用久了,app越来越臃肿,老手机卡顿成常态。这里给大家推荐个改善老手机使用体验的方法,还能帮我们卸载不需要的app。 手机现状 如今的app不断更新,看似在优化,实则内存占用越来越大,对手机性…...

迁移科技3D视觉系统:重塑纸箱拆垛场景的智能革命
一、传统拆垛场景的困局与破局之道 在汽车零部件仓库中,每天有超过2万只异形纸箱需要拆垛分拣。传统人工拆垛面临三大挑战: 效率瓶颈:工人每小时仅能处理200-300件,且存在间歇性疲劳安全隐患:20kg以上重箱搬运导致年…...
