计算机图形学:liang算法和Cyrus-Beck算法
其中Cyrus-Beck算法呢,是计算一根直线一个多边形的交线段;
liang算法是Cyrus的一个特例,即多边形刚好是矩形;
先看看Cyrus算法的思路【从别的博客找的图片】:
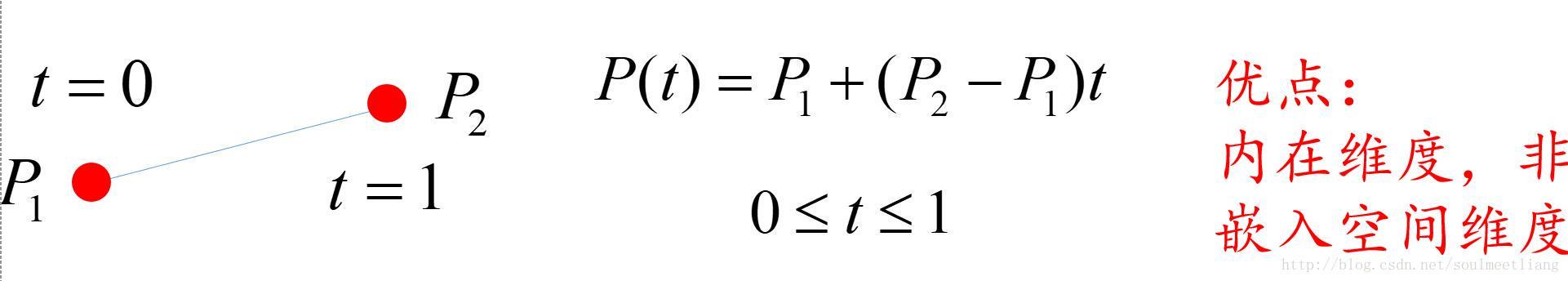


这很容易理解,点积>0时就可能中内部嘛,这就限定了t[直线参数]的一个范围,每个这样的边限定的范围的交集就是t的范围;
这种范围又分为很多种不同的范围,一种是左限制[-nan,i],一种是右限制[i,+nan];
这种限制在代数上的意义,是这样推断的,我会给出更形象的个人理解;

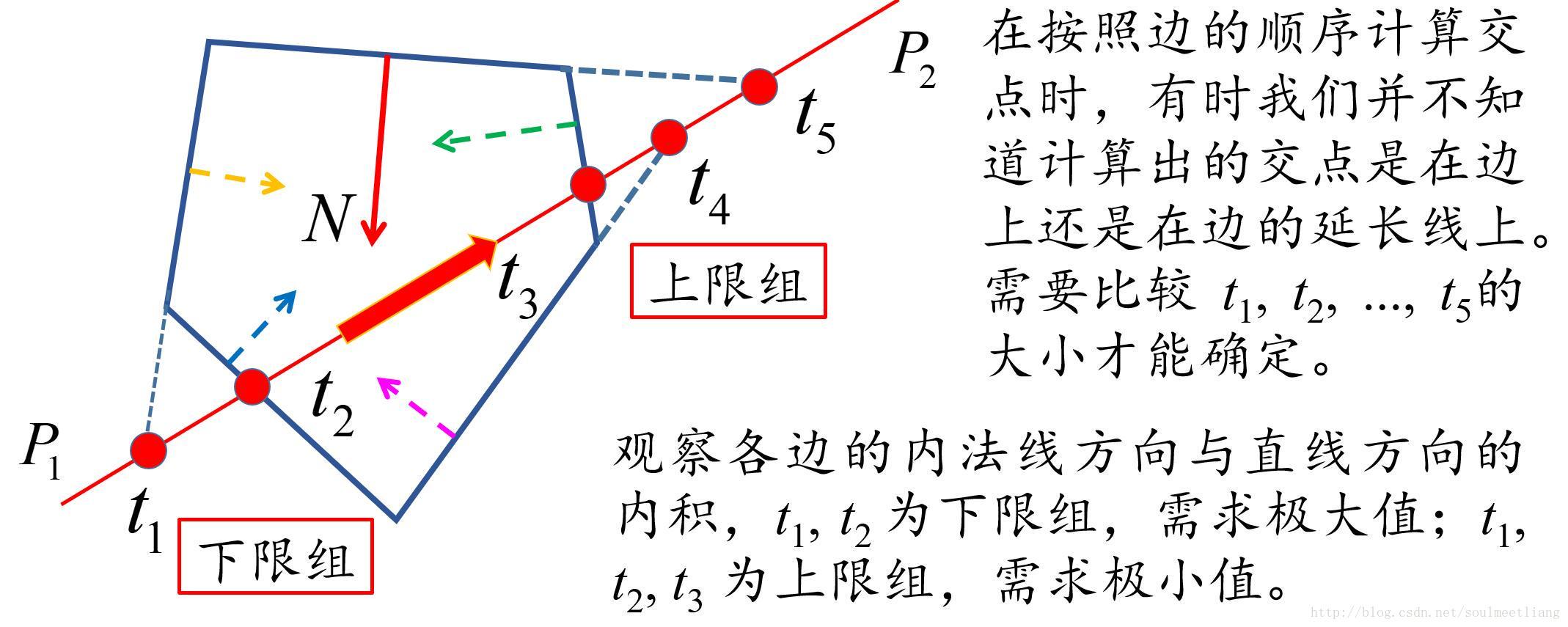
好,我们分成了上限组和下限组,其实这样的几何意义就已经很好理解了;
我个人弄了个更好理解的版本,看啊;
其实上限组顾名思义,其中的线段给出的限定,可以确定t的一个上限,下限组也顾名思义;
那么有了上限和下限,那么确定的t的范围;
拿上面那张图中的N想来和P1P2向量举例子,N向量在P1P2向量的分量是不是向左的?那么N就是属于上限组,分量在P1P2上向右的向量就是下限组;

然后来看看liang算法;
我很好奇,为什么要把这两个算法分开?这是一模一样的的算法;
我刚刚在书上看liang算法的时候一头雾水,变量一代换,中间逻辑直接少了几个环节,看个毛线;
然后去网上查了一下才懂了;
先看看书上的解释:

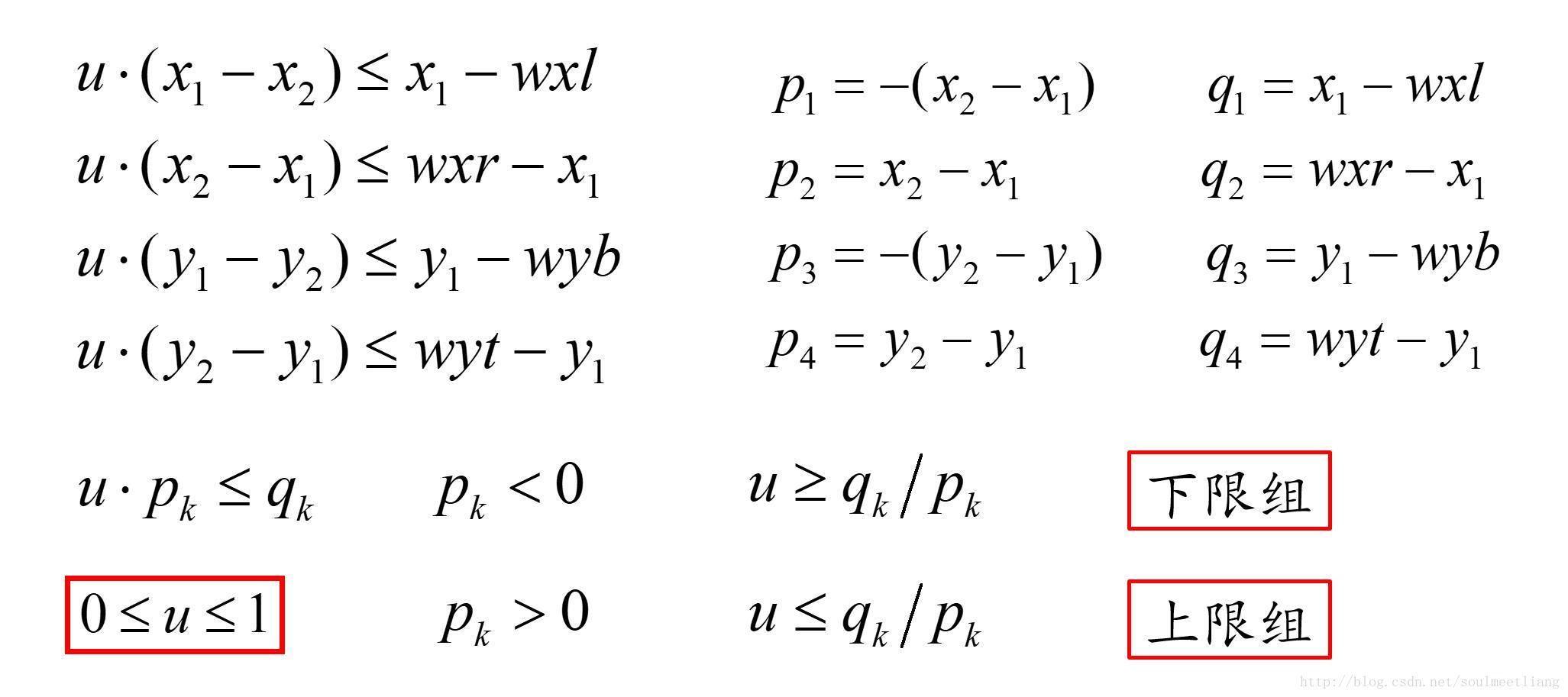
也是确定了上限组和下限组,这张图还好,起码给了上下限组的概念,有的书是完全不给这个概念的;
其实我们可以直接看推:
线段的端点P1(x1,y1),P2(x2,y2)
左边界xl(-lx,0) 右边界xr(lx,0) 下边界yb(0,-lx) 上边界yt(0,lx);
所以左右边界的内法向量就是[1,0]、[-1,0]
上下边界也一样[0,1]、[0,-1]
那么我们只需要看四个向量在P1P2向量上的分量是向左还是向右就可以知道哪个是上限组哪个是下限组了,当然P1指向P2的方向是向右;
最后的公式也是表示这个意思的;
最后我还有一个发现,但应该也被人发现过,那就是P1P2与四条边界的交点为q1,q2,q3,q4的话,在P1P2与矩形有交集的前提下,对这六个点的x坐标[y坐标也行]进行排序,那么第3、4个点就是需要显示的线段的端点
相关文章:
计算机图形学:liang算法和Cyrus-Beck算法
其中Cyrus-Beck算法呢,是计算一根直线一个多边形的交线段;liang算法是Cyrus的一个特例,即多边形刚好是矩形;先看看Cyrus算法的思路【从别的博客找的图片】:这很容易理解,点积>0时就可能中内部嘛…...

React组件之间的通信方式总结(上)
先来几个术语: 官方我的说法对应代码React elementReact元素let element<span>A爆了</span>Component组件class App extends React.Component {}无App为父元素,App1为子元素<App><App1></App1></App> 本文重点&…...

C++17 nodiscard标记符
文章目录前言弃值表达式nodiscard标记符函数非弃值声明类/枚举类/结构 非弃值声明返回类引用与类指针前言 在C 17中引入了一个标记符nodiscard,用于声明一个 “非弃值(no-discard)表达式”。那么在开始之前,我们需要了解一下什么是弃值表达式。 弃值表…...

SAP 寄售业务的标准流程
SAP的标准寄售业务,供应商提供的物料只有在公司使用之后才需支付应付账款,类似是一种先吃后付钱的餐饮流程。 SAP的寄售流程把实际业务中的供应商,采购方收货,采购方消耗物料,采购方依据消耗物料数量进行付款ÿ…...

操作系统高频知识
目录 一、线程与进程的区别 区别: 二、多进程和多线程区别 三、进程与程序的区别 三、死锁 1、是什么 2、产生的原因 3、产生的必要条件(4个) 4、如何预防 5、如何避免 6、如何检测 7、如何解除 一、线程与进程的区别 1、线程&a…...

加载预训练模型,模型微调,在自己的数据集上快速出效果
针对于某个任务,自己的训练数据不多,先找到一个同类的别人训练好的模型,把别人现成的训练好了的模型拿过来,换成自己的数据,调整一下参数,再训练一遍,这就是微调(fine-tuneÿ…...
VScode远程连接服务器-过程试图写入的管道不存在-could not establist connection to【已解决】
问题描述 使用服务器的过程中突然与服务器断连,报错如下:could not establist connection to [20:23:39.487] > ssh: connect to host 10.201.0.131 port 22: Connection timed out > [20:23:39.495] > 过程试图写入的管道不存在。 > [20…...
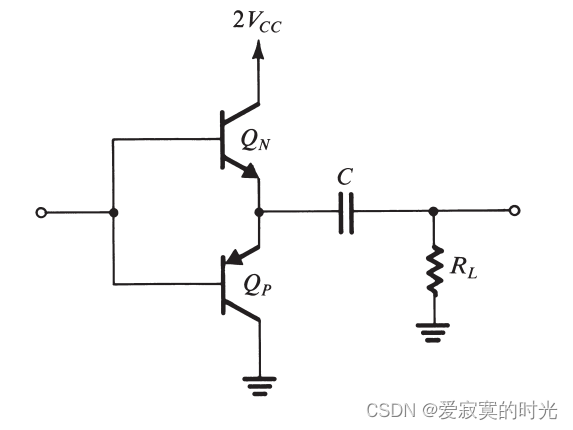
电子技术——B类输出阶
电子技术——B类输出阶 下图展示了一个B类输出阶的原理图,B类输出阶由两个互补的BJT组成,不同时导通。 原理 当输入电压 vI0v_I 0vI0 的时候,两个晶体管都截止输出电压为零。当 vIv_IvI 上升至超过0.5V的时候,此时 QNQ_NQN…...
【老卫搬砖】034期:HarmonyOS 3.1 Beta 1初体验,我在本地模拟器里面刷短视频
今天啊打开这个DevEco Studio的话,已经提示有3.1Beta1版本的一个更新啊。然后看一下它的一些特性。本文也演示了如何在本地模拟器里面运行HarmonyOS版短视频。 主要特性 新特性包括: Added support for Windows 11 64-bit and macOS 13.x OSs, as well…...

Day901.内部临时表 -MySQL实战
内部临时表 Hi,我是阿昌,今天学习记录的是关于内部临时表的内容。 sort buffer、内存临时表和 join buffer。这三个数据结构都是用来存放语句执行过程中的中间数据,以辅助 SQL 语句的执行的。 其中,在排序的时候用到了 sort bu…...

jstatd的启动方式与关闭方式
启动方式与注意事项: 启动方式: 前台启动不打印日志: jstatd -J-Djava.security.policyjstatd.all.policy -J-Djava.rmi.server.hostname服务器IP 前台启动并打印日志: ./jstatd -J-Djava.security.policyjstatd.all.policy -…...

_improve-3
createElement过程 React.createElement(): 根据指定的第一个参数创建一个React元素 React.createElement(type,[props],[...children] )第一个参数是必填,传入的是似HTML标签名称,eg: ul, li第二个参数是选填,表示的是属性&#…...
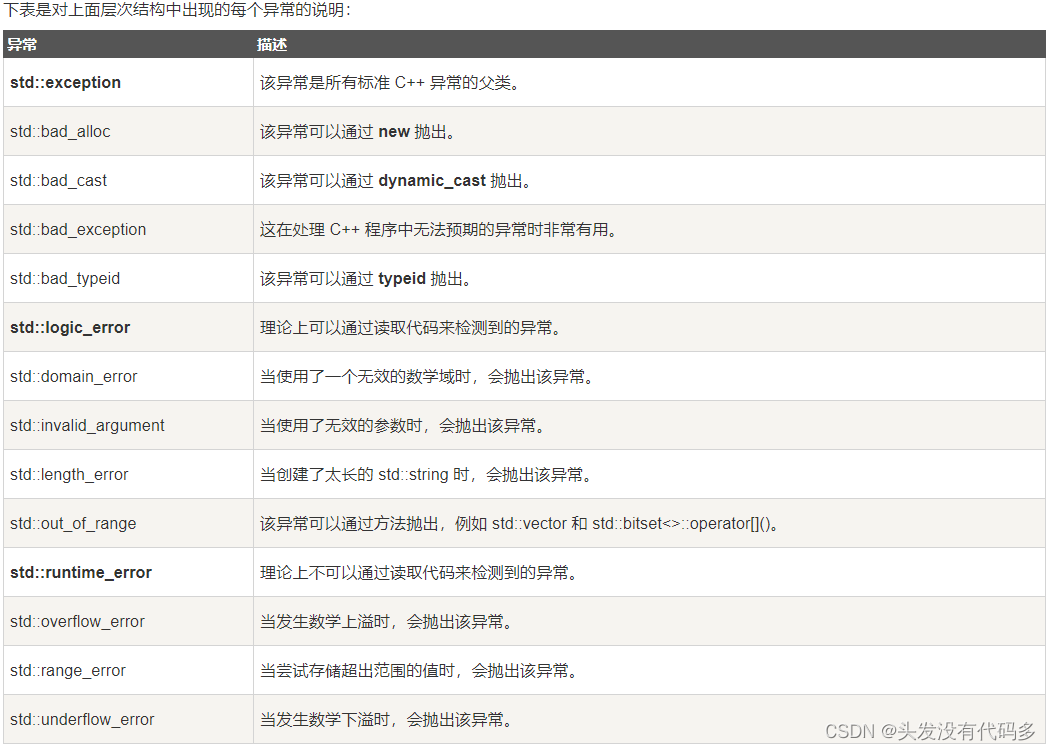
C++——异常
目录 C语言传统的处理错误的方式 C异常概念 异常的使用 异常的抛出和匹配原则 在函数调用链中异常栈展开匹配原则 自定义异常体系 异常的重新抛出 编辑 异常安全 异常规范 C标准库的异常体系 异常的优缺点 C语言传统的处理错误的方式 传统的错误处理机制: …...
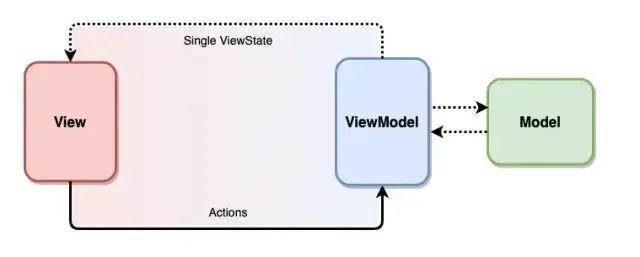
MVVM 架构进阶:MVI 架构详解
前言Android开发发展到今天已经相当成熟了,各种架构大家也都耳熟能详,如MVC,MVP,MVVM等,其中MVVM更是被官方推荐,成为Android开发中的显学。不过软件开发中没有银弹,MVVM架构也不是尽善尽美的,在使用过程中…...
有没有必要考PMP证书?
其实针对有没有必要考试吗,这个可以根本不同行业的人来决定的。 1.高等教育项目管理专业科班出身的人员。 在我国本科学历和硕士研究生学历中,项目管理也有开设。不管以后从事的工作是否为项目管理或其他管理,作为本专业的同学,…...
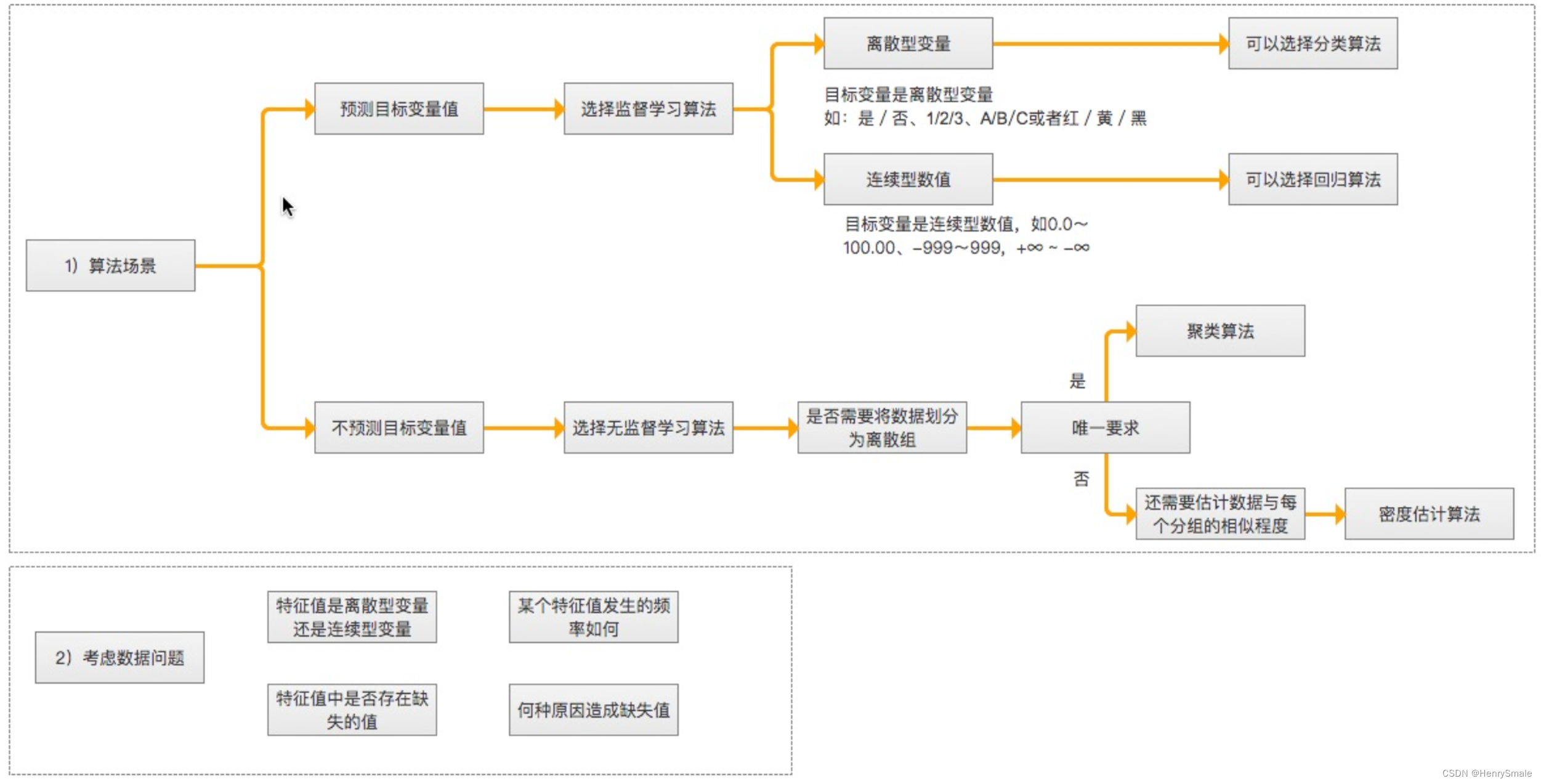
1 机器学习基础
1 机器学习概述 1.1 数据驱动的问题求解 大数据-Big Data 大数据的多面性 1.2 数据分析 机器学习:海量的数据,获取有用的信息 专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之…...
java基础系列(六) sleep()和wait() 区别
一.前言 关于并发编程这块, 线程的一些基础知识我们得搞明白, 本篇文章来说一下这两个方法的区别,对Android中的HandlerThread机制原理可以有更深的理解, HandlerThread源码理解,请查看笔者的这篇博客: HandlerThread源码理解_handlerthread 源码_broadview_java的博客-CSDN博…...

Urho3D序列化
从Serializable派生的类可以通过定义属性将其自动序列化为二进制或XML格式。属性存储到每个类的上下文中。场景加载/保存和网络复制都是通过从Serializable派生Node和Component类来实现的。 支持的属性类型是Variant支持的所有属性类型,不包括指针和自定义值。 属性…...
企业级信息系统开发学习1.3——利用注解配置取代Spring配置文件
文章目录一、利用注解配置类取代Spring配置文件(一)打开项目(二)创建新包(三)拷贝类与接口(四)创建注解配置类(五)创建测试类(六)运行…...

VUE DIFF算法之快速DIFF
VUE DIFF算法系列讲解 VUE 简单DIFF算法 VUE 双端DIFF算法 文章目录VUE DIFF算法系列讲解前言一、快速DIFF的代码实现二、实践练习1练习2总结前言 本节我们来写一下VUE3中新的DIFF算法-快速DIFF,顾名思义,也就是目前最快的DIFF算法(在VUE中&…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
)
后端下载限速(redis记录实时并发,bucket4j动态限速)
✅ 使用 Redis 记录 所有用户的实时并发下载数✅ 使用 Bucket4j 实现 全局下载速率限制(动态)✅ 支持 动态调整限速策略✅ 下载接口安全、稳定、可监控 🧩 整体架构概览 模块功能Redis存储全局并发数和带宽令牌桶状态Bucket4j Redis分布式限…...
