【题解 线段树】[蓝桥杯 2022 省 A] 选数异或
题目描述:
[蓝桥杯 2022 省 A] 选数异或
题目描述
给定一个长度为 n n n 的数列 A 1 , A 2 , ⋯ , A n A_{1}, A_{2}, \cdots, A_{n} A1,A2,⋯,An 和一个非负整数 x x x, 给定 m m m 次查询, 每次询问能否从某个区间 [ l , r ] [l, r] [l,r] 中选择两个数使得他们的异或等于 x x x 。
输入格式
输入的第一行包含三个整数 n , m , x n, m, x n,m,x 。
第二行包含 n n n 个整数 A 1 , A 2 , ⋯ , A n A_{1}, A_{2}, \cdots, A_{n} A1,A2,⋯,An。
接下来 m m m 行,每行包含两个整数 l i , r i l_{i}, r_{i} li,ri 表示询问区间 [ l i , r i ] \left[l_{i}, r_{i}\right] [li,ri] 。
输出格式
对于每个询问, 如果该区间内存在两个数的异或为 x x x 则输出 yes, 否则输出 no。
样例 #1
样例输入 #1
4 4 1
1 2 3 4
1 4
1 2
2 3
3 3
样例输出 #1
yes
no
yes
no
提示
【样例说明】
显然整个数列中只有 2,3 的异或为 1 。
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, 1 ≤ n , m ≤ 100 1 \leq n, m \leq 100 1≤n,m≤100;
对于 40 % 40 \% 40% 的评测用例, 1 ≤ n , m ≤ 1000 1 \leq n, m \leq 1000 1≤n,m≤1000;
对于所有评测用例, 1 ≤ n , m ≤ 1 0 5 , 0 ≤ x < 2 20 , 1 ≤ l i ≤ r i ≤ n 1 \leq n, m \leq 10^5,0 \leq x<2^{20}, 1 \leq l_{i} \leq r_{i} \leq n 1≤n,m≤105,0≤x<220,1≤li≤ri≤n , 0 ≤ A i < 2 20 0 \leq A_{i}<2^{20} 0≤Ai<220 。
蓝桥杯 2022 省赛 A 组 D 题。
分析:
对于异或,我们有如下性质:
a x o r b = c − > a x o r c = b a\ xor\ b=c->a\ xor\ c=b a xor b=c−>a xor c=b
于是问题就转化成:
∃ i ∈ [ l , r ] , ∃ j ∈ [ l , r ] \exists i\in[l,r],\exists j\in[l,r] ∃i∈[l,r],∃j∈[l,r],有 a [ j ] = a [ i ] x o r x a[j]=a[i]\ xor\ x a[j]=a[i] xor x
对于每一个 i i i,我们如何寻找合法的 j j j呢?
对于一个 i i i,如果他有若干个合法的j,我们显然只要找到最近的那个j就可以了。
我们用一个数组 L a [ i ] La[i] La[i]表示数字 i i i上次出现的位置
那么对于位置 i i i,他最近的一个j的位置就是 L a [ a [ i ] x o r x ] La[a[i]\ xor\ x] La[a[i] xor x]
这样我们就找到了每个数字最近的合法数字的位置。
那么对于一个区间 [ l , r ] [l,r] [l,r],我们如何进行求解呢?
由于题目中的问题是问我们是否存在这样一对数字满足条件
也就是说这是一个存在性问题,只要存在一对合法的数字即可
就是说:
∃ i ∈ [ l , r ] , 有 L a [ i ] > = l \exists i\in[l,r],有La[i]>=l ∃i∈[l,r],有La[i]>=l
因此我们只需要对区间 [ l , r ] [l,r] [l,r]之间所有的 L a [ i ] La[i] La[i]求一个最大值即可
线段树可以维护
Code
#include<bits/stdc++.h>
using namespace std;const int N = 1e5+10;
map < int , int > Now,La;
int n,m,k;struct Tr{int tr[4*N];void Insert(int x,int l,int r,int po,int v){if (l == r){tr[x] = v; return;}int Mid = (l+r)>>1;if (po <= Mid) Insert(x<<1,l,Mid,po,v);else Insert(x<<1|1,Mid+1,r,po,v);tr[x] = max(tr[x<<1],tr[x<<1|1]);return ;}int Ask(int x,int l,int r,int L,int R){if (L <= l && r <= R) return tr[x];int Mid = l+r>>1;int Max = 0;if (L <= Mid) Max = max(Max,Ask(x<<1,l,Mid,L,R));if (R > Mid) Max = max(Max,Ask(x<<1|1,Mid+1,r,L,R));return Max;}
}tr;int a[N];int main(){scanf("%d %d %d",&n,&m,&k);for (int i = 1; i <= n; i++) scanf("%d",&a[i]);for (int i = 1; i <= n; i++){int x = 0;if (Now.count(a[i]^k)) x = Now[a[i]^k];Now[a[i]] = i;tr.Insert(1,1,n,i,x);}for (int i = 1; i <= m; i++){int l,r; scanf("%d %d",&l,&r);int Max = tr.Ask(1,1,n,l,r);if (Max >= l) printf("yes\n");else printf("no\n");}return 0;
}
相关文章:

【题解 线段树】[蓝桥杯 2022 省 A] 选数异或
题目描述: [蓝桥杯 2022 省 A] 选数异或 题目描述 给定一个长度为 n n n 的数列 A 1 , A 2 , ⋯ , A n A_{1}, A_{2}, \cdots, A_{n} A1,A2,⋯,An 和一个非负整数 x x x, 给定 m m m 次查询, 每次询问能否从某个区间 [ l , r ] [l, r] [l,r] 中选择两…...

宠物喂食器方案智能开发设计
现在年轻人特别是在一、二、三线城市的,工作节奏快、加班、出差、旅游成常态,无法经常在宠物身边照看,宠物智能自动喂食机能够解放宠主的双手和解决不能长时间在处的无奈,很好地满足了年轻宠物主照顾宠物的需求。宠物主和宠物都需…...

chatgpt综述阅读理解
Summary of ChatGPT-Related research and perspective towards the future of large language models 摘要 本文总结了语言模型在遵循指令和人类反馈方面的相关工作,包括训练语言模型来理解指令并按照指令执行任务,以及提高语言模型的性能和理解能力的…...

XCTF-RSA-2:baigeiRSA2、 cr4-poor-rsa
baigeiRSA2 题目描述 import libnum from Crypto.Util import number from functools import reduce from secret import flagn 5 size 64 while True:ps [number.getPrime(size) for _ in range(n)]if len(set(ps)) n:breake 65537 n reduce(lambda x, y: x*y, ps) m …...
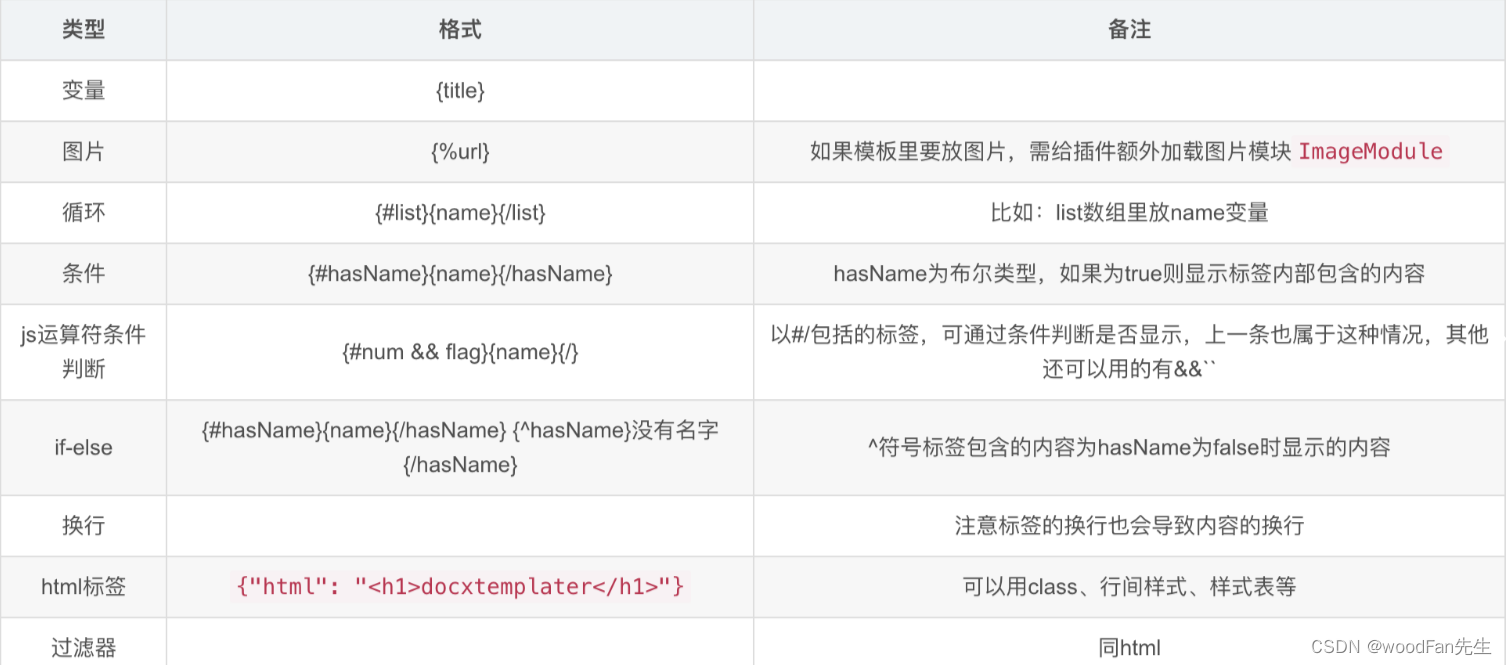
js 根据word文档模板导出内容
一、创建word导出模板 1、本地创建一个test.docx 2、将最终需要的文档内容及样式编辑完成(图1) 3、将所需动态值的位置,替换为变量参数(图2) 注: 动态值书写 图1 图2 模板值的书写要求 二、项目中使用 1、安装依赖 npm install docxtemplater-image-module-free --save n…...

AIGC | 如何用“Flow”,轻松解决复杂业务问题
随着LLM(大语言模型)的爆火,不少企业都在寻找通过LLM解决企业业务问题的方法,以达到降本增效的效果。但是,当面对较为复杂的业务问题(如:背景资料多、问题分类多、条件判断复杂、涉及模块多等&a…...

多级菜单 树结构 排序 前端 后端 java
目录 省流: 正文: v1.0版 前端传的值: 后端代码: v2.0版 v3.0版 省流: 前端提交过来整个树即可。 给整个树进行sort。代码如下: public static void sort(List<Node> tree){int i 0;for…...
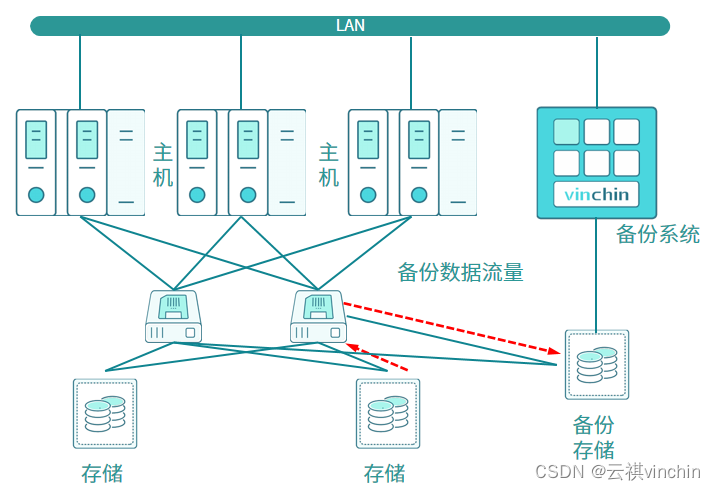
LAN-Free在数据备份时的应用与优势
在灾备领域中,常见的备份架构有LAN、LAN-Free和Server-Free备份,其中LAN备份架构图见图1,LAN-Free备份架构图见图2,Server-Free备份架构图见图3,途中红色箭头为备份数据流量走向: 图 1 图 2 图 3 从图1、图…...

HTML 文档声明和语言设置
HTML 文档声明 DOCTYPE 文档类型声明,用于告诉浏览器的解析器,该以那种 HTML 版本来解析这个文件。 HTML 5 版本声明 <!DOCTYPE html>XHTML 1.0 严格版声明 <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN" "http:/…...

【C++基础知识学习笔记】精华版(复习专用)
常用语法 函数重载(Overload) 规则: 函数名相同 参数个数不同、参数类型不同、参数顺序不同 注意: 返回值类型与函数重载无关 调用函数时,实参的隐式类型转换可能会产生二义性 默认参数 C++ 允许函数设置默认参数,在调用时可以根据情况省略实参。规则如下: 默认参数只能…...
探索ChatGPT在学术写作中的应用与心得
随着人工智能的迅猛发展,ChatGPT作为一种强大的自然语言处理模型,逐渐在学术界引起了广泛的关注。本文将探讨ChatGPT在学术写作中的应用,并分享使用ChatGPT进行学术写作时的一些经验和心得。 01 — ChatGPT在学术写作中的应用 1.文献综述和…...

Android:怎么学习才能更好的进大厂呢?
怎么学习才能更好的进大厂呢? 很多朋友都在问这个问题。 其实没有什么特别的技巧,就是依靠自己的毅力和决心。一天做不到,就一个月;一个月做不到,就一年。只要有决心,无论学历或资历如何,都不是…...

CSS标点符号换行问题
最近遇到一个奇怪的现象,元素中中文文本正常显示,但是加了一堆符号后中文文本居然换行了. div{width: 200px;border: 1px solid blue;word-break: break-all;} <div>文本</div>经过研究发现,因为标点符号不允许出现在行首和行尾,连带着符号…...
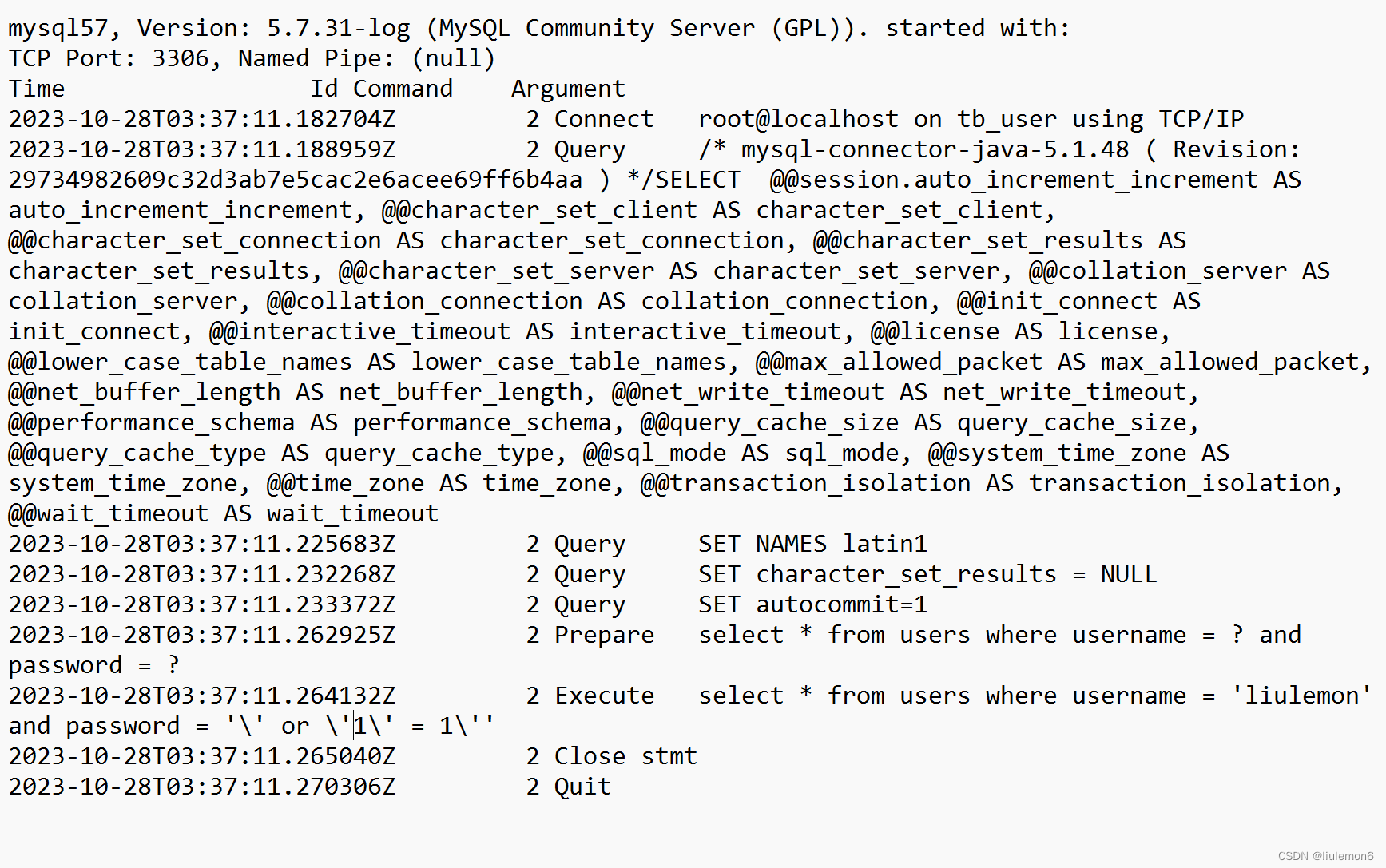
jdbc Preparestatement防止SQL注入的原理
2023-10-28T03:37:11.264132Z 2 Execute select * from users where username liulemon and password \ or \1\ 1\ 可以看到这一行,预编译时?变成了转义字符 useServerPrepStmtstrue加上这句才能预编译...

如何控制 LLM 的输出格式和解析其输出结果?
现在很多人对于如何使用像 ChatGPT 这样的 LLM 已经比较有经验了,可以使用各种不同的 Prompt 得到自己想要的结果。但有时候我们的使用场景不局限于手动操作,而是需要结合程序去调用 API,并且解析 API 的返回结果,从而实现一些自动…...

【Linux】 ps 命令使用
ps (英文全拼:process status)命令用于显示当前进程的状态,类似于 windows 的任务管理器。 语法 ps [选项] ps命令 -Linux手册页 著者 ps最初由布兰科兰克斯特撰写<lankestefwi.uva.nl>。迈克尔K约翰逊<johnsonmred…...

C++二分查找算法的应用:长度递增组的最大数目
本文涉及的基础知识点 二分查找 题目 给你一个下标从 0 开始、长度为 n 的数组 usageLimits 。 你的任务是使用从 0 到 n - 1 的数字创建若干组,并确保每个数字 i 在 所有组 中使用的次数总共不超过 usageLimits[i] 次。此外,还必须满足以下条件&…...

提示3D标题编辑器仍在运行怎么解决,以及3D标题编辑器怎么使用
在进行视频剪辑时,尤其是剪辑一些带有文字的开场视频,一般都会使用具有立体效果的3D标题,这样制作出来的视频效果不仅好看,还非常的炫酷,但是对于一些刚刚开始接触视频剪辑的小伙伴来说,可能对3D标题还不是…...
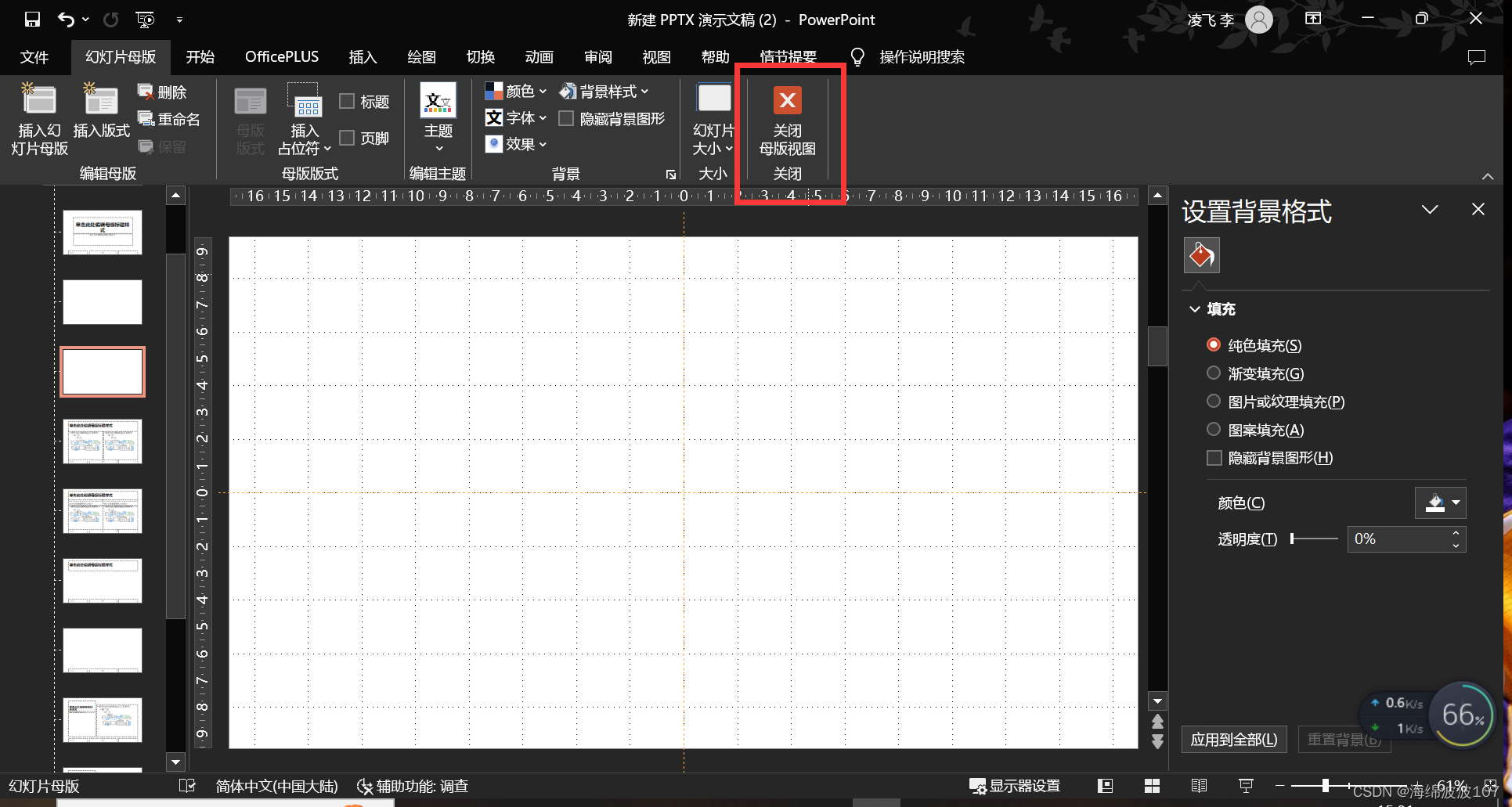
1. PPT高效初始化设置
1. PPT高效初始化设置 软件安装:Office 2019 主题和颜色 颜色可以在白天与黑夜切换,护眼 切换成了黑色 撤回次数 撤回次数太少,只有20次怎么办 自动保存 有时忘记保存就突然关闭,很需要一个自动保存功能 图片压缩 图…...

el-cascader级联选择器选中一个全选中问题
问题 只选中一个却把同级全选中 解决 :props中添加label、value、children属性 label、value、children属性值需要和后端返回的集合中的字段名保持一致 后端返回数据:...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
