【数据结构】单链表OJ题

前言:
本节博客将讲解单链表的反转,合并有序链表,寻找中间节点及约瑟夫问题
文章目录
- 一、反转链表
- 二、合并有序链表
- 三、链表的中间结点
- 四、环形链表的约瑟夫问题
一、反转链表
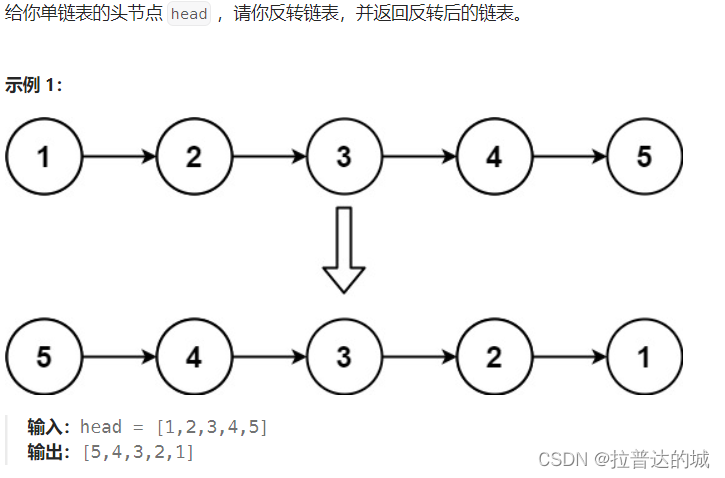
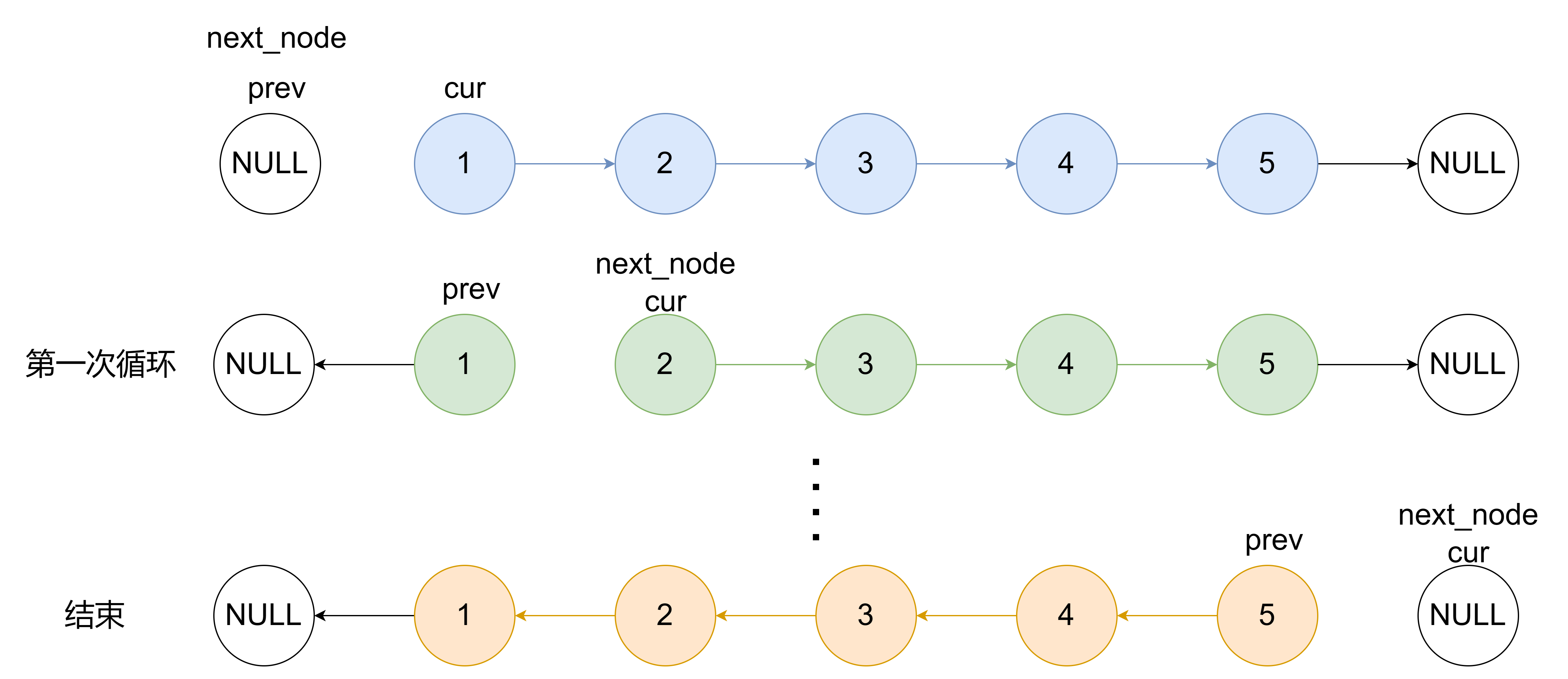
要反转链表,我们需要遍历链表并改变每个节点的 next 指针,使其指向其前一个节点。为了完成这个任务,我们需要三个指针:prev、cur和 next_node。
- prev:保存当前节点的前一个节点。初始化为 NULL,因为链表的新头部(原始链表的尾部)的 next 指针将指向 NULL。
- cur:表示当前正在处理的节点。
- next_node:保存当前节点的下一个节点。
struct ListNode* reverseList(struct ListNode* head) {typedef struct ListNode ListNode;ListNode* prev = NULL;ListNode* cur = head;ListNode* next_node = NULL;while (cur != NULL) {next_node = cur->next; // 保存当前节点的下一个节点cur->next = prev; // 更新当前节点的next指针prev = cur; // 将prev移动到当前节点cur = next_node; // 移动到下一个节点}return prev; // 返回新的头部
}
二、合并有序链表
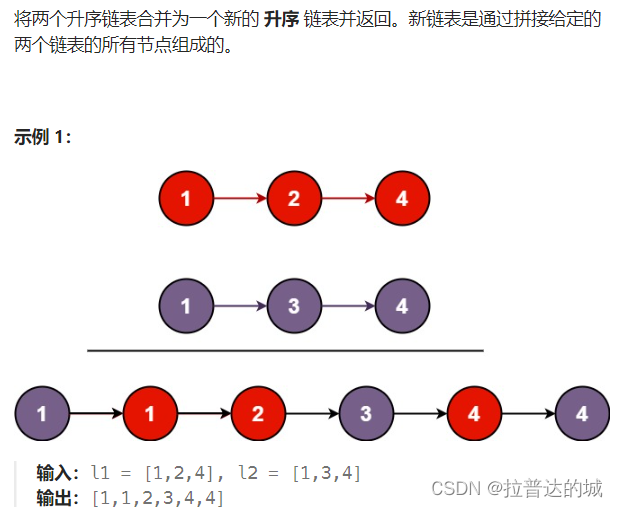
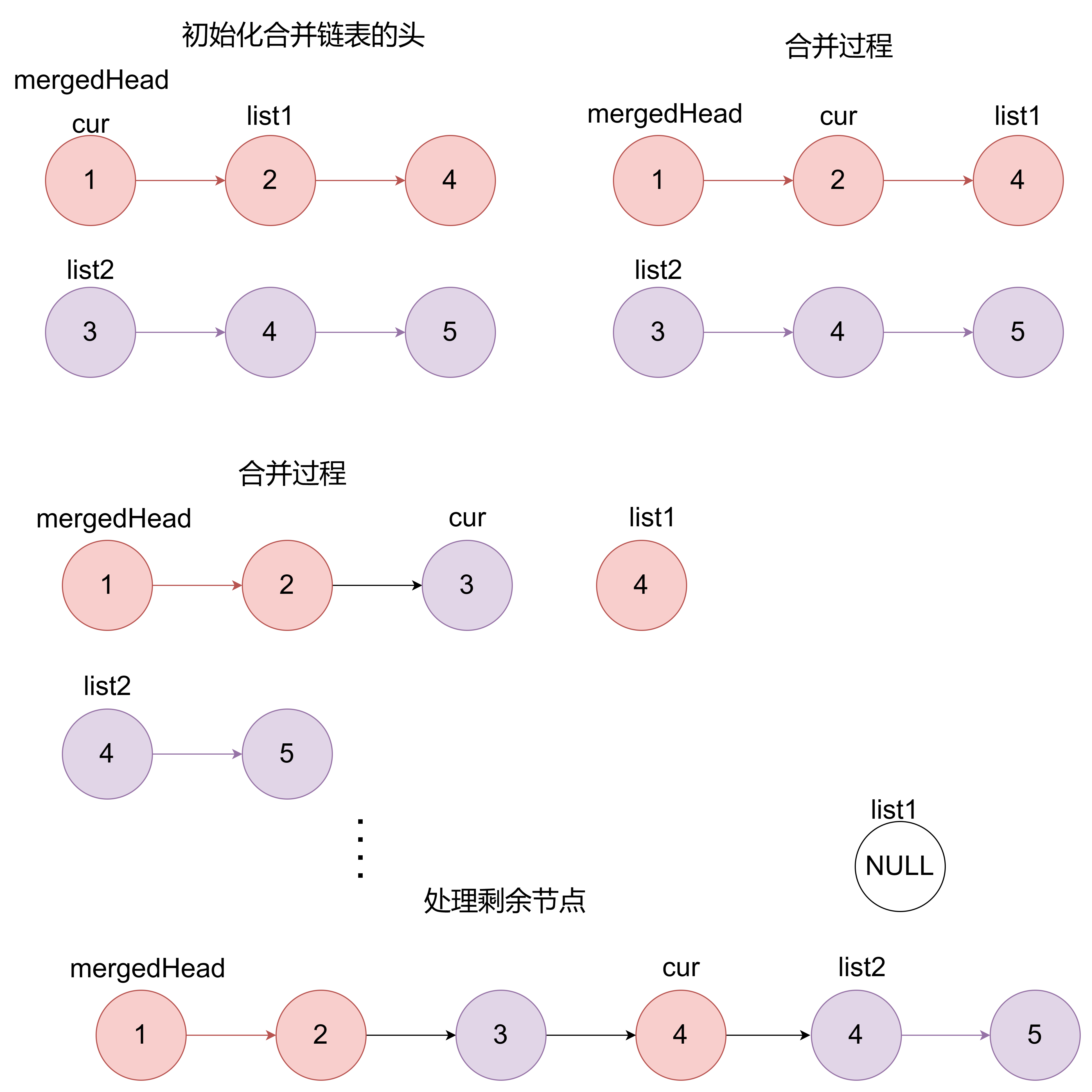
分为四个步骤:
- 开始阶段: 首先,函数检查两个列表是否为空。如果其中一个为空,则直接返回另一个列表,因为没有合并的必要。
- 初始化合并链表的头: 函数接着检查list1和list2的首个节点,看哪一个的值较小。较小的那个节点将成为新的合并链表的首个节点。
- 合并过程: 使用一个while循环来遍历list1和list2,每次循环会从这两个列表中选择一个较小的节点,并将其添加到合并列表的末尾。
- 处理剩余节点: 循环结束后,list1和list2可能还有未处理的节点。以下的代码将剩余的节点添加到合并列表的末尾。
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {//开始阶段if (!list1) return list2;if (!list2) return list1;//初始化合并链表的头ListNode* mergedHead = NULL; // 合并后的链表头if (list1->val < list2->val) {mergedHead = list1;list1 = list1->next;} else {mergedHead = list2;list2 = list2->next;}ListNode* cur = mergedHead; // 指向合并后链表的当前节点//合并过程while (list1 && list2) {if (list1->val <= list2->val) {cur->next = list1;list1 = list1->next;} else {cur->next = list2;list2 = list2->next;}cur = cur->next;}//处理剩余节点// 如果list1还有剩余节点if (list1) {cur->next = list1;}// 如果list2还有剩余节点if (list2) {cur->next = list2;}return mergedHead;
}
三、链表的中间结点
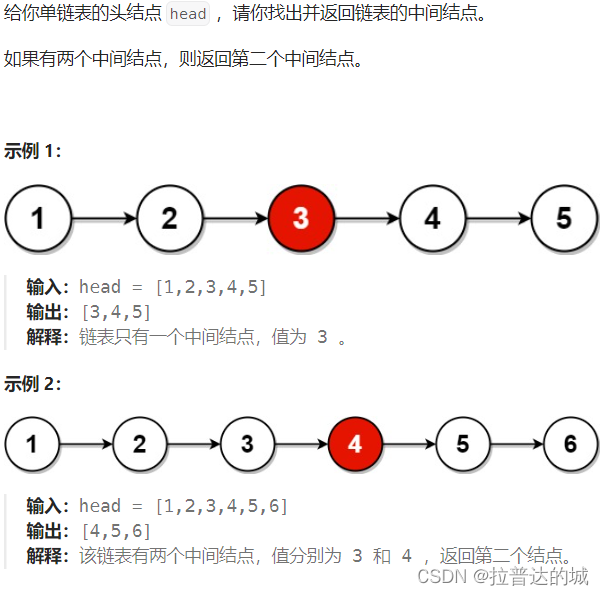
这题我们可以使用快慢指针,在循环中,fast 指针每次移动两个节点,而 slow 指针每次只移动一个节点。这意味着,当 fast 指针到达链表的末尾时,slow 指针将位于链表的中间位置。
typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) {ListNode* fast = head;ListNode* slow = head;while(fast && fast->next){slow = slow->next;fast = fast->next->next;}return slow;
}
四、环形链表的约瑟夫问题

以下是代码的主要思路:
- 数据结构选择:
使用单向循环链表来模拟这个问题。循环链表是一个适合此问题的数据结构,因为当链表到达末尾时,它可以自动回到头部。 - 链表节点创建:
ListBuyNode(int x):这个函数用于创建一个新的链表节点,它接受一个整数值 x 作为参数,并返回一个新的链表节点。 - 循环链表创建:
CreateList(int n):这个函数用于创建一个有 n 个节点的单向循环链表。链表的节点值从 1 到 n。链表的最后一个节点指向头节点,使其形成一个循环。 - 约瑟夫环算法:
- ysf(int n, int m):这个函数实现了约瑟夫环的主要算法。
- 首先,它调用 CreateList(n) 来创建一个 n 个节点的单向循环链表。
- 使用两个指针,prev 和 cur,分别表示当前节点的前一个节点和当前节点。
- 使用一个计数器 count 从 1 开始计数,每次循环增加计数器的值。
- 当 count 达到 m 时,当前的 cur 节点将被删除(淘汰),并释放其内存。然后,cur 指向下一个节点,并且计数器重置为 1。
- 如果 count 不等于 m,prev 和 cur 都向前移动一个节点,继续循环。
- 当链表只剩下一个节点时(即 cur->next 等于 cur 时),循环结束。
- 返回最后一个剩下的节点的值,即最后一个被淘汰的人的位置。
// 定义链表节点结构
typedef struct ListNode ListNode;// 分配内存并创建一个链表节点,值为x
ListNode* ListBuyNode(int x){ListNode* node = (ListNode*)malloc(sizeof(ListNode)); // 分配内存if(node == NULL){ // 检查内存分配是否成功perror("Malloc fail;");exit(1); // 分配失败,退出程序}node->val = x; // 设置节点的值node->next = NULL; // 初始化下一个节点为NULLreturn node; // 返回创建的节点
}// 创建一个包含n个节点的单向循环链表
ListNode* CreateList(int n){ListNode* phead = ListBuyNode(1); // 创建头节点,值为1ListNode* pTail = phead; // 初始化尾节点为头节点for(int i = 2; i <= n; i++){ // 从2到n循环创建节点ListNode* node = ListBuyNode(i); // 创建新节点pTail->next = node; // 把新节点连接到链表的尾部pTail = pTail->next; // 更新尾节点为新创建的节点}pTail->next = phead; // 将链表的尾部连接到头部,使其成为一个循环链表return pTail; // 返回链表的尾节点
}// 约瑟夫环问题的解决函数
int ysf(int n, int m ) {ListNode* prev = CreateList(n); // 创建一个单向循环链表,并返回尾节点ListNode* cur = prev->next; // 当前节点从头节点开始int count = 1; // 计数器初始化为1while(cur->next != cur){ // 当链表只剩下一个节点时停止循环if(count == m){ // 当计数器达到m时prev->next = cur->next; // 删除当前节点free(cur); // 释放当前节点的内存cur = prev->next; // 更新当前节点为下一个节点count = 1; // 重置计数器}else{prev = cur; // 否则,移动到下一个节点cur = cur->next;count++; // 增加计数器}}return cur->val; // 返回最后剩下的节点的值
}
如果你喜欢这篇文章,点赞👍+评论+关注⭐️哦!
欢迎大家提出疑问,以及不同的见解。
相关文章:

【数据结构】单链表OJ题
前言: 本节博客将讲解单链表的反转,合并有序链表,寻找中间节点及约瑟夫问题 文章目录 一、反转链表二、合并有序链表三、链表的中间结点四、环形链表的约瑟夫问题 一、反转链表 要反转链表,我们需要遍历链表并改变每个节点的 next 指针&#…...

智能工厂架构
引:https://www.bilibili.com/video/BV1Vs4y167Kx/?spm_id_from=333.788&vd_source=297c866c71fa77b161812ad631ea2c25 智能工厂框架 智能工厂五层系统框架 MES 数据共享 <...

阿里云多款ECS产品全面升级 性能最多提升40%
“阿里云始终围绕‘稳定、安全、性能、成本、弹性’的目标不断创新,为客户创造业务价值。”10月31日,杭州云栖大会上,阿里云弹性计算计算产品线负责人张献涛表示,通过持续的产品和技术创新,阿里云发布了HPC优化实例等多…...
)
责任链模式(Chain of Responsibility)
责任链模式是对象的行为模式。使多个对象都有机会处理请求,从而避免请求的发送者和接受者直接的耦合关系。 public abstract class Handler {protected Handler successor;public abstract void handlerRequest(String condition);protected Handler getSuccessor()…...
文件管理技巧:根据大小智能分类并移动至目标文件夹
在文件管理过程中,我们经常需要整理大量的文件。根据文件的大小,将其智能分类并移动至目标文件夹,可以帮助我们更高效地管理文件,提高工作效率。通过使用云炫文件管理器可以根据文件大小进行智能分类和移动至目标文件夹࿰…...

具有自主产权的SaaS门店收银系统全套源码输出
PHPMysql前后端分离, 小程序线上商城; 进销存管理库存盘点, 多仓库库存调拨, 会员系统。 消费者扫码查价系统。...
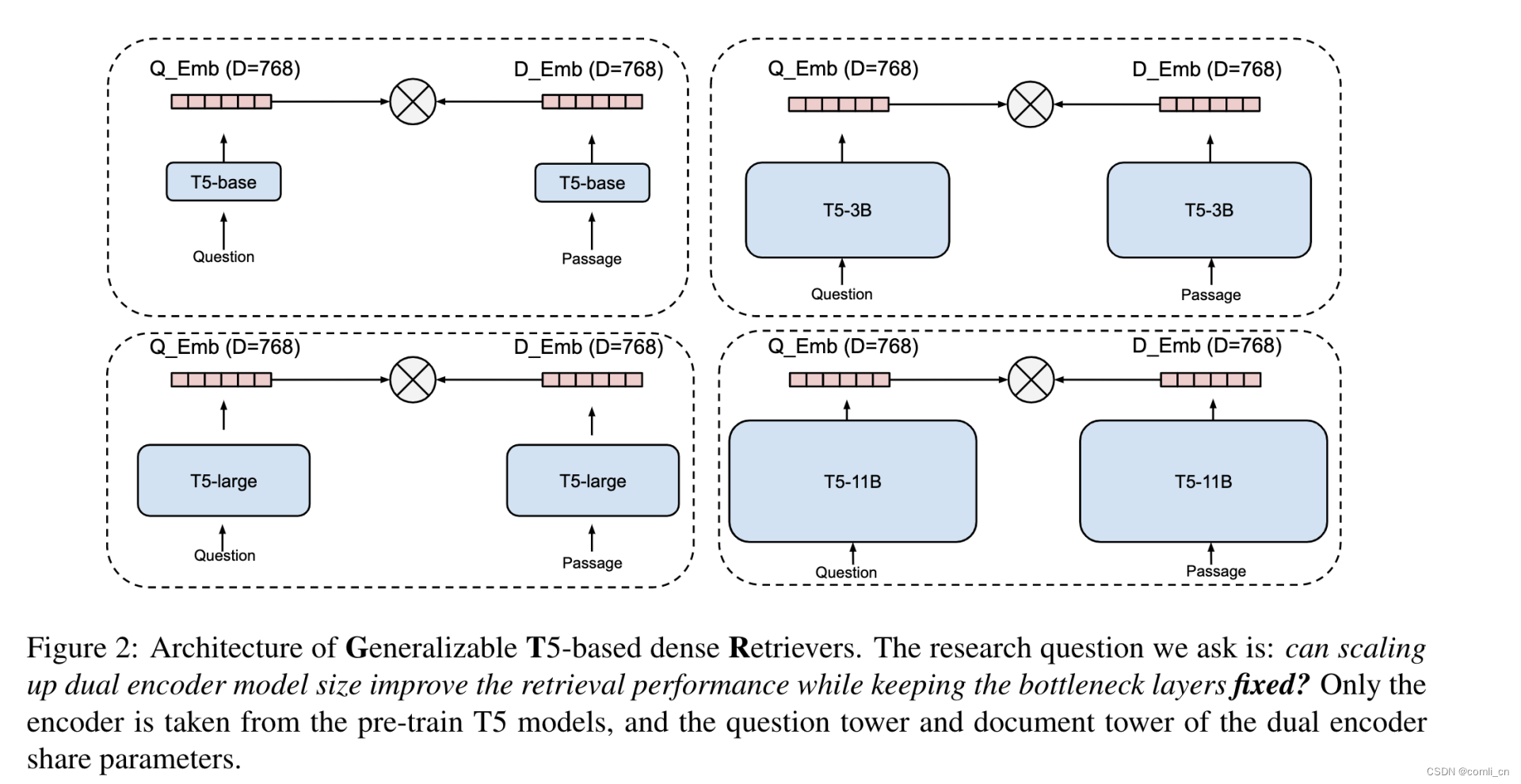
论文阅读:One Embedder, Any Task: Instruction-Finetuned Text Embeddings
1. 优势 现存的emmbedding应用在新的task或者domain上时表现会有明显下降,甚至在相同task的不同domian上的效果也不行。这篇文章的重点就是提升embedding在不同任务和领域上的效果,特点是不需要用特定领域的数据进行finetune而是使用instuction finetun…...

[BUUCTF NewStarCTF 2023 公开赛道] week3 crypto/pwn
居然把第3周忘了写笔记了. 后边难度上来了,还是很有意思的 Crypto Rabins RSA rsa一般要求e与phi互质,但rabin一般用2,都是板子题也没什么好解释的 from Crypto.Util.number import * from secret import flag p getPrime(64) q getPrime(64) assert p % 4 3 assert q %…...
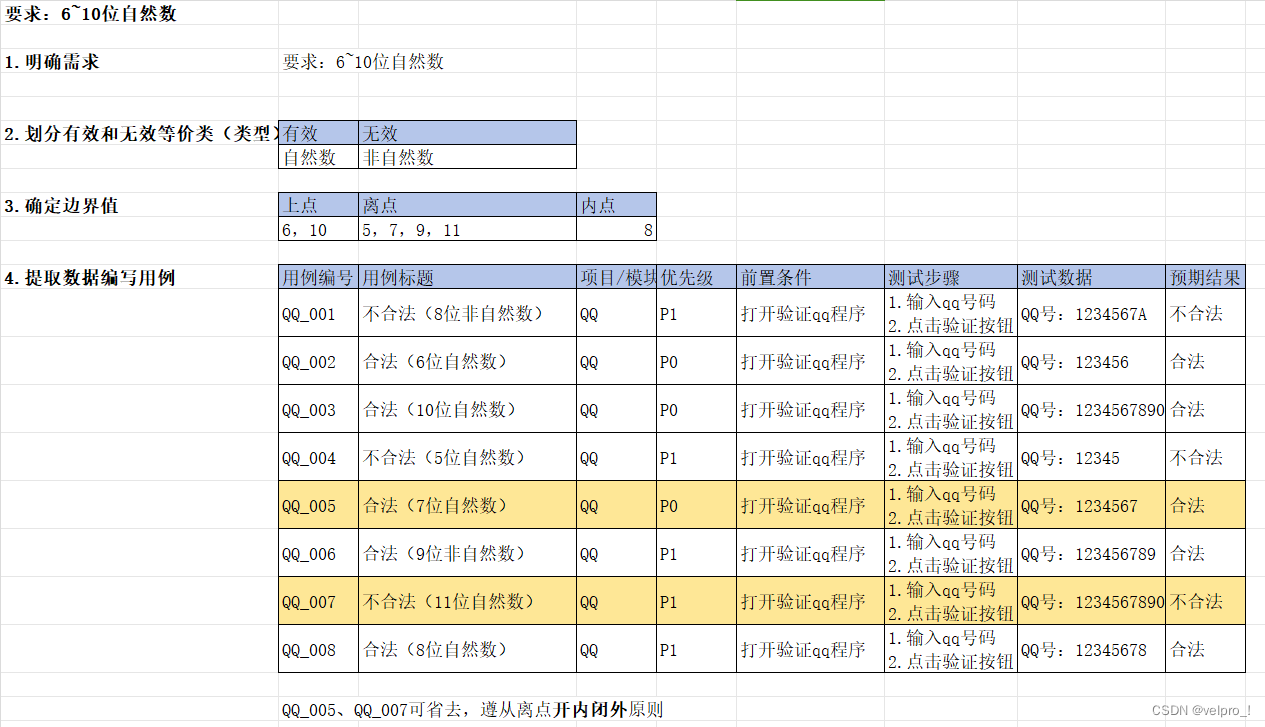
软件测试---边界值分析(功能测试)
能对限定边界规则设计测试点---边界值分析 选取正好等于、刚好大于、刚好小于边界的值作为测试数据 上点: 边界上的点 (正好等于);必选(不考虑区开闭) 内点: 范围内的点 (区间范围内的数据);必选(建议选择中间范围) 离点: 距离上点最近的点 (刚好…...
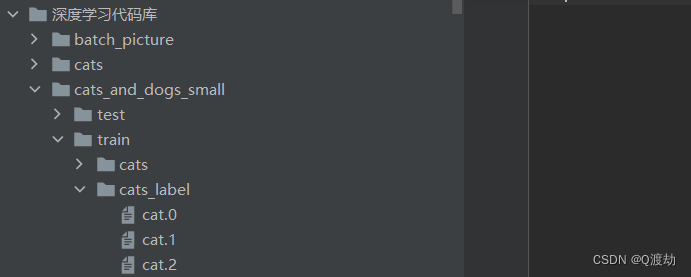
使用pytorch处理自己的数据集
目录 1 返回本地文件中的数据集 2 根据当前已有的数据集创建每一个样本数据对应的标签 3 tensorboard的使用 4 transforms处理数据 tranfroms.Totensor的使用 transforms.Normalize的使用 transforms.Resize的使用 transforms.Compose使用 5 dataset_transforms使用 1 返回本地…...

http进一步认识
好久不见各位,今天为大家带来http协议的进一步认识 文章目录 👀http协议的认识👀新的改变 👀http协议的认识 http协议经历了三个版本的演化,HTTP0.9是第一个版本的协议,它的组成极其简单,只涉…...

grafana docker安装
grafana docker安装 Grafana是一款用Go语言开发的开源数据可视化工具,可以做数据监控和数据统计,带有告警功能。目前使用grafana的公司有很多,如paypal、ebay、intel等。 Grafana 是 Graphite 和 InfluxDB 仪表盘和图形编辑器。Grafana 是开…...
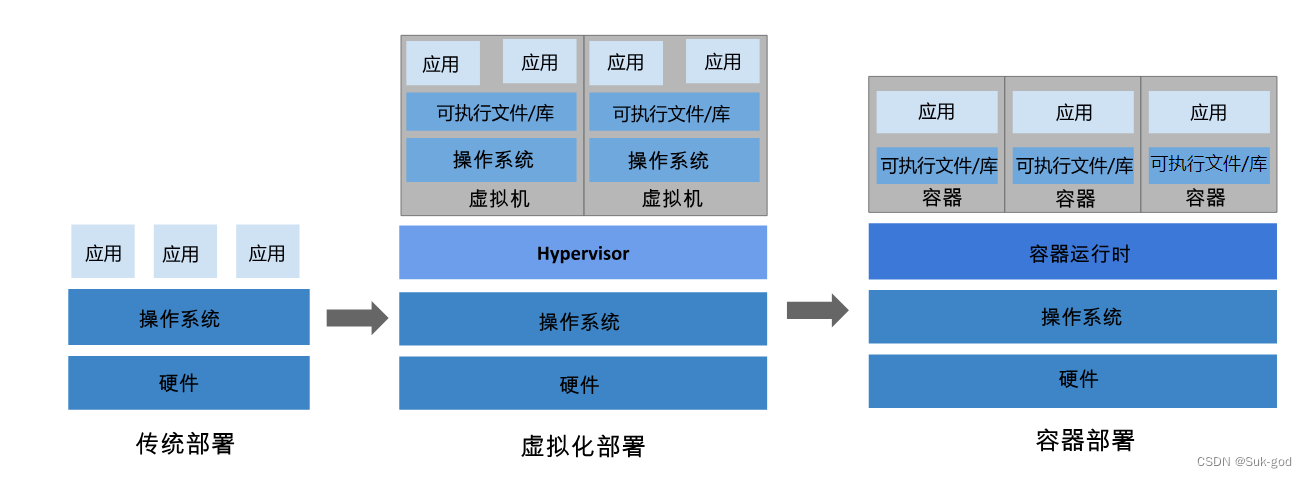
【Kubernetes】初识k8s--扫盲阶段
文章目录 1、k8s概述2、为什么要有k8s2.1 回顾以往的应用部署方式2.2 容器具有的优势 3、k8s能带来什么 1、k8s概述 kubernetes是一个可移植、可扩展的开源平台,用于管理 容器化 的工作负载和服务,可促进申明式配置和自动化。kubernetes拥有一个庞大且快…...

“01”滴答“摩尔斯电码”加密解密单个字符
“01”替换滴嗒“.-”“摩尔斯电码”字符,加密解密键盘输入的单个字符。 (本笔记适合熟悉循环和列表的 coder 翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”教程《 python 完全自学教程》&a…...

P3817 小A的糖果
Portal. 贪心。 注意到这里的盒子不会被删除,只会改变盒子的值。问题立刻简单化了。对于一组相邻的糖果个数和大于 x x x 的盒子组,优先吃掉靠后的盒子。 证明正确性也很显然,因为减少后面的盒子的糖果数可以使得后面的情况更优。 #incl…...
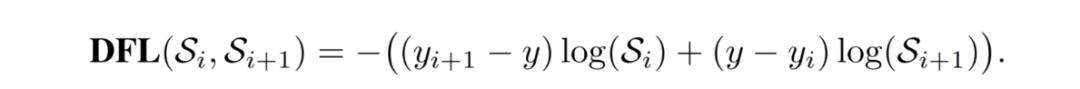
Yolov8目标识别与实例分割——算法原理详细解析
前言 YOLO是一种基于图像全局信息进行预测并且它是一种端到端的目标检测系统,最初的YOLO模型由Joseph Redmon和Ali Farhadi于2015年提出,并随后进行了多次改进和迭代,产生了一系列不同版本的YOLO模型,如YOLOv2、YOLOv3、YOLOv4&a…...

HandlerMethodArgumentResolver方法参数解析器支持多用户
1、概述 HandlerMethodArgumentResolver,中文称为方法参数解析器,是Spring Web(SpringMVC)组件中的众多解析器之一,主要用来对Controller中方法的参数进行处理。 使用场景 在一般的接口调用场景下,每次调用Controller都需要检查请求中的token信息,并根据token还原用户信息…...

【Linux】 man命令使用
介绍 man命令是Linux下最核心的命令之一。而man命令也并不是英文单词“man”的意思,它是单词manual的缩写,即使用手册的意思。 man命令会列出一份完整的说明。 其内容包括命令语法、各选项的意义及相关命令 。更为强大的是,不仅可以查看Lin…...

同一个数据库服务器进行数据表间的数据迁移-MySQL
同一个数据库服务器进行数据表间的数据迁移 一、相同结构的表数据迁移/备份/导入到同一MySQL的某个库的某张表 实验目标:将t1.table_one的数据备份到migration_one.table_11(提醒:这两个表结构一致) 同一个MySQL中有很多库&…...

适用于 Linux 的 WPF:Avalonia
许多年前,在 WPF 成为“Windows Presentation Foundation”并将 XAML 作为 .NET、Windows 等的 UI 标记语言引入之前,有一个代号为“Avalon”的项目。Avalon 是 WPF 的代号。XAML 现在无处不在,XAML 标准是一个词汇规范。 Avalonia 是一个开…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...
