16- TensorFlow实现线性回归和逻辑回归 (TensorFlow系列) (深度学习)
知识要点
线性回归要点:
- 生成线性数据: x = np.linspace(0, 10, 20) + np.random.rand(20)
- 画点图: plt.scatter(x, y)
- TensorFlow定义变量: w = tf.Variable(np.random.randn() * 0.02)
- tensor 转换为 numpy数组: b.numpy()
- 定义优化器: optimizer = tf.optimizers.SGD()
- 定义损失: tf.reduce_mean(tf.square(y_pred - y_true)) # 求均值
- 自动微分: tf.GradientTape()
- 计算梯度: gradients = g.gradient(loss, [w, b])
- 更新w, b: optimizer.apply_gradients(zip(gradients, [w, b]))
逻辑回归要点:
- 查看安装文件: pip list
- 聚类数据生成器: make_blobs
- 生成聚类数据: data, target = make_blobs(centers = 3)
- 转换为tensor 数据: x = tf.constant(data, dtype = tf.float32)
- 定义tensor变量: B = tf.Variable(0., dtype = tf.float32)
- 矩阵运算: tf.matmul(x, W)
- 返回值长度为batch_size的一维Tensor: tf.sigmoid(linear)
- 调整形状: y_pred = tf.reshape(y_pred, shape = [100])
- tf.clip_by_value(A, min, max):输入一个张量A,把A中的每一个元素的值都压缩在min和max之间。
- 求均值: tf.reduce_mean()
- 定义优化器: optimizer = tf.optimizers.SGD()
- 计算梯度: gradients = g.gradient(loss, [W, B]) # with tf.GradientTape() as g
- 迭代更新W, B: optimizer.apply_gradients(zip(gradients, [W, B]))
- 准确率计算: (y_ == y_true).mean()
1 使用tensorflow实现 线性回归
实现一个算法主要从以下三步入手:
-
找到这个算法的预测函数, 比如线性回归的预测函数形式为:y = wx + b,
-
找到这个算法的损失函数 , 比如线性回归算法的损失函数为最小二乘法
-
找到让损失函数求得最小值的时候的系数, 这时一般使用梯度下降法.
使用TensorFlow实现算法的基本套路:
-
使用TensorFlow中的变量将算法的预测函数, 损失函数定义出来.
-
使用梯度下降法优化器求损失函数最小时的系数
-
分批将样本数据投喂给优化器,找到最佳系数
1.1 导包
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression1.2 生成线性数据
# 生成线性数据
x = np.linspace(0, 10, 20) + np.random.rand(20)
y = np.linspace(0, 10, 20) + np.random.rand(20)
plt.scatter(x, y)
1.3 初始化斜率变量
# 把w,b 定义为变量
w = tf.Variable(np.random.randn() * 0.02)
b = tf.Variable(0.)
print(w.numpy(), b.numpy()) # -0.031422824 0.01.4 定义线性模型和损失函数
# 定义线性模型
def linear_regression(x):return w * x +b# 定义损失函数
def mean_square_loss(y_pred, y_true):return tf.reduce_mean(tf.square(y_pred - y_true))1.5 定义优化过程
# 定义优化器
optimizer = tf.optimizers.SGD()
# 定义优化过程
def run_optimization():# 把需要求导的计算过程放入gradient pape中执行,会自动实现求导with tf.GradientTape() as g:pred = linear_regression(x)loss = mean_square_loss(pred, y)# 计算梯度gradients = g.gradient(loss, [w, b])# 更新w, boptimizer.apply_gradients(zip(gradients, [w, b]))1.6 执行迭代训练过程
# 训练
for step in range(5000):run_optimization() # 持续迭代w, b# z展示结果if step % 100 == 0:pred = linear_regression(x)loss = mean_square_loss(pred, y)print(f'step:{step}, loss:{loss}, w:{w.numpy()}, b: {b.numpy()}')
1.7 线性拟合
linear = LinearRegression() # 线性回归
linear.fit(x.reshape(-1, 1), y)plt.scatter(x, y)
x_test = np.linspace(0, 10, 20).reshape(-1, 1)
plt.plot(x_test, linear.coef_ * x_test + linear.intercept_, c='r') # 画线
plt.plot(x_test, w.numpy() * x_test + b.numpy(), c='g', lw=10, alpha=0.5) # 画线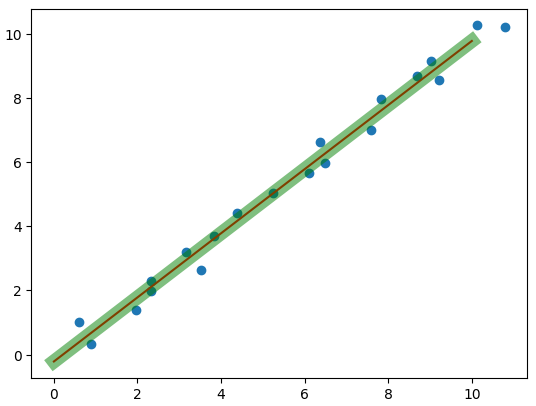
2. 使用TensorFlow实现 逻辑回归
实现逻辑回归的套路和实现线性回归差不多, 只不过逻辑回归的目标函数和损失函数不一样而已.
使用tensorflow实现逻辑斯蒂回归
- 找到预测函数 :
- 找到损失函数 : -(y_true * log(y_pred) + (1 - y_true)log(1 - y_pred))
- 梯度下降法求损失最小的时候的系数
2.1 导包
import tensorflow as tf
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt- 聚类数据生成器: make_blobs
2.2 描聚类数据点
data, target = make_blobs(centers = 3)
plt.scatter(data[:, 0] , data[:, 1], c = target)
x = data.copy()
y = target.copy()
print(x.shape, y.shape) # (100, 2) (100,)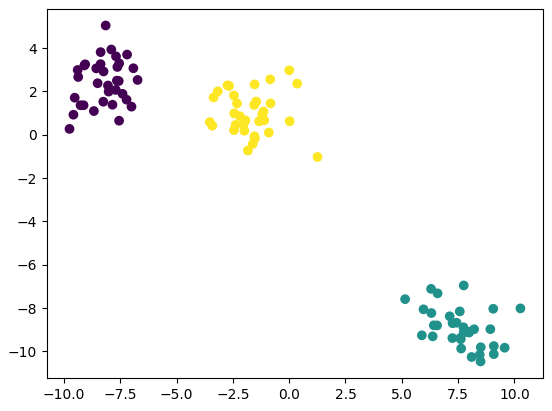
2.3 数据转换为张量 (tensor)
x = tf.constant(data, dtype = tf.float32)
y = tf.constant(target, dtype = tf.float32)2.4 定义预测函数
# 定义预测变量
W = tf.Variable(np.random.randn(2, 1) * 0.2, dtype = tf.float32)
B = tf.Variable(0., dtype = tf.float32)2.5 定义目标函数
def sigmoid(x):linear = tf.matmul(x, W) + Breturn tf.nn.sigmoid(linear)2.6 定义损失
# 定义损失
def cross_entropy_loss(y_true, y_pred):# y_pred 是概率,存在可能性是0, 需要进行截断y_pred = tf.reshape(y_pred, shape = [100])y_pred = tf.clip_by_value(y_pred, 1e-9, 1)return tf.reduce_mean(-(tf.multiply(y_true, tf.math.log(y_pred)) + tf.multiply((1 - y_pred),tf.math.log(1 - y_pred))))2.7 定义优化器
# 定义优化器
optimizer = tf.optimizers.SGD()def run_optimization():with tf.GradientTape() as g:# 计算预测值pred = sigmoid(x) # 结果为概率loss = cross_entropy_loss(y, pred)#计算梯度gradients = g.gradient(loss, [W, B])# 更新W, Boptimizer.apply_gradients(zip(gradients, [W, B]))2.8 定义准确率
# 计算准确率
def accuracy(y_true, y_pred):# 需要把概率转换为类别# 概率大于0.5 可以判断为正例y_pred = tf.reshape(y_pred, shape = [100])y_ = y_pred.numpy() > 0.5y_true = y_true.numpy()return (y_ == y_true).mean()2.9 开始训练
# 定义训练过程
for i in range(5000):run_optimization()if i % 100 == 0:pred = sigmoid(x)acc = accuracy(y, pred)loss = cross_entropy_loss(y, pred)print(f'训练次数:{i}, 准确率: {acc}, 损失: {loss}')
相关文章:

16- TensorFlow实现线性回归和逻辑回归 (TensorFlow系列) (深度学习)
知识要点 线性回归要点: 生成线性数据: x np.linspace(0, 10, 20) np.random.rand(20)画点图: plt.scatter(x, y)TensorFlow定义变量: w tf.Variable(np.random.randn() * 0.02)tensor 转换为 numpy数组: b.numpy()定义优化器: optimizer tf.optimizers.SGD()定义损失: …...

无自动化测试系统设计方法论
灵活 敏捷 迭代。 自动化测试 辩思 测试必不可少 想想看没有充分测试的代码, 哪一次是一次过的? 哪一次不需要经历下测试的鞭挞? 不要以为软件代码容易改, 就对于质量不切实际的自信—那是自大! 不适用自动化测试的case 遗留系统。太多的依赖方, 不想用过多的mock > …...
架构初探-学习笔记
1 什么是架构 有关软件整体结构与组件的抽象描述,用于指导软件系统各个方面的设计。 1.1 单机架构 所有功能都实现在一个进程里,并部署在一台机器上。 1.2 单体架构 分布式部署单机架构 1.3 垂直应用架构 按应用垂直切分的单体架构 1.4 SOA架构 将…...

在成都想转行IT,选择什么专业比较好?
很多创新型的互联网服务公司的核心其实都是软件,创新的基础、运行的支撑都是软件。例如,软件应用到了出租车行业,就形成了巅覆行业的滴滴;软件应用到了金融领域,就形成互联网金融;软件运用到餐饮行业,就形成美团;软件运…...
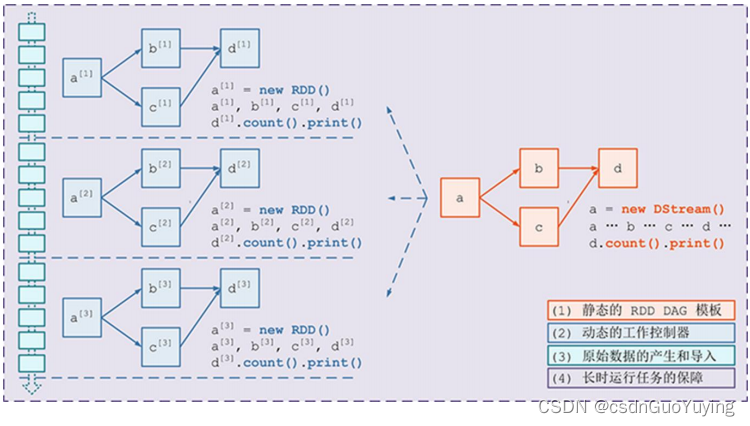
【Spark分布式内存计算框架——Spark Streaming】4.入门案例(下)Streaming 工作原理
2.3 Streaming 工作原理 SparkStreaming处理流式数据时,按照时间间隔划分数据为微批次(Micro-Batch),每批次数据当做RDD,再进行处理分析。 以上述词频统计WordCount程序为例,讲解Streaming工作原理。 创…...
2、算法先导---思维能力与工具
题目 碎纸片的拼接复原(2013B) 内容 破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用。传统上,拼接复原工作需由人工完成,准确率较高,但效率很低。特别是当碎片数量巨大,人工拼接很难在短时…...

WordPress 函数:add_theme_support() 开启主题自定义功能(全面)
add_theme_support() 用于在我们的当前使用的主题添加一些特殊的功能,函数一般写在主题的functions.php文件中,当然也可以再插件中使用钩子来调用该函数,如果是挂在钩子上,那他必须挂在after_setup_theme钩子上,因为 i…...

Winform控件开发(16)——Timer(史上最全)
前言: Timer控件的作用是按用户定义的时间间隔引发事件的计时器,说的直白点就是,他就像一个定时炸弹一样到了一定时间就爆炸一次,区别在于定时炸弹炸完了就不会再次爆炸了,但是Timer这个计时器到了下一个固定时间还会触发一次,上面那张图片就是一个典型的计时器,该定时器…...

游戏高度可配置化:通用数据引擎(data-e)及其在模块化游戏开发中的应用构想图解
游戏高度可配置化:通数据引擎在模块化游戏开发中的应用构想图解 ygluu 码客 卢益贵 目录 一、前言 二、模块化与插件 1、常规模块化 2、插件式模块化(插件开发) 三、通用数据引擎理论与构成 1、名字系统(数据类型…...
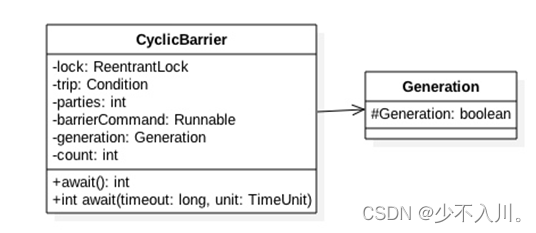
CountDownLatch与CyclicBarrier原理剖析
1.CountDownLatch 1.1 什么是CountDownLatch CountDownLatch是一个同步工具类,用来协调多个线程之间的同步,或者说起到线程之间的通信(而不是用作互斥的作用)。 CountDownLatch能够使一个线程在等待另外一些线程完成各自工作之…...
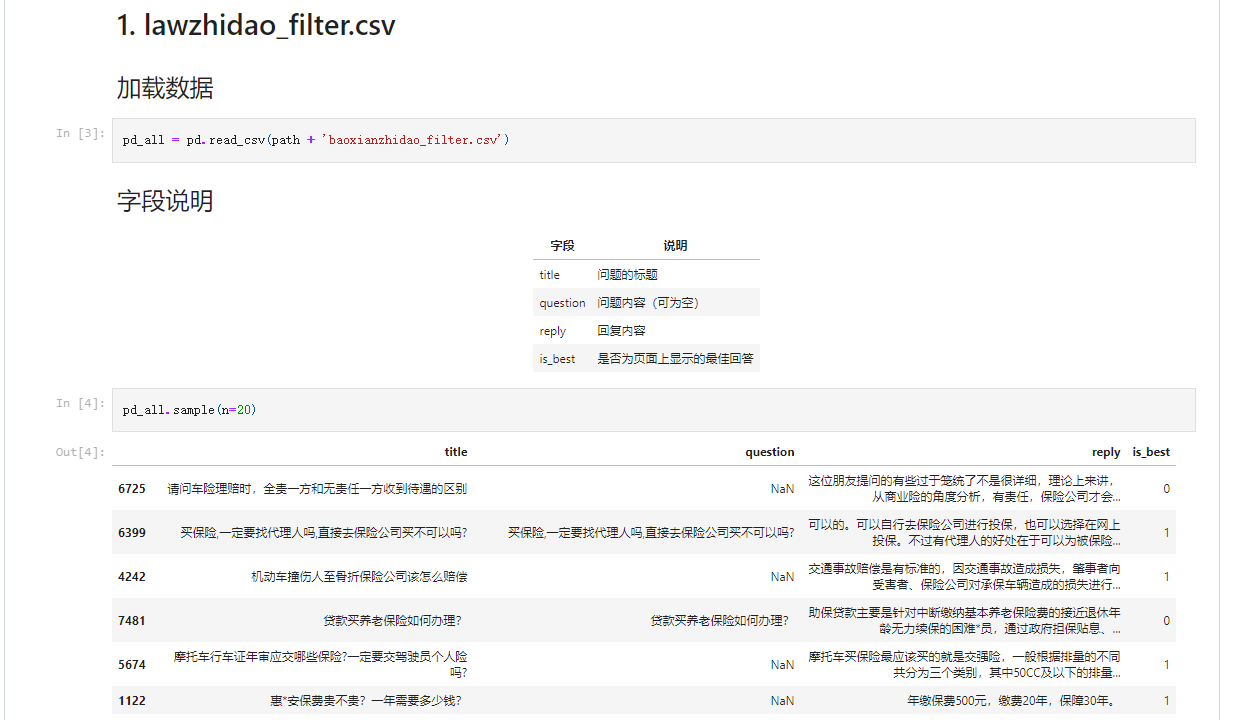
NLP中的对话机器人——预训练基准模型
引言 本文是七月在线《NLP中的对话机器人》的视频笔记,主要介绍FAQ问答型聊天机器人的实现。 场景二 上篇文章中我们解决了给定一个问题和一些回答,从中找到最佳回答的任务。 在场景二中,我们来实现: 给定新问题,从…...

C语言学习及复习笔记-【14】C文件读写
14 C文件读写 14.1打开文件 您可以使用 fopen( ) 函数来创建一个新的文件或者打开一个已有的文件,这个调用会初始化类型 FILE 的一个对象,类型 FILE包含了所有用来控制流的必要的信息。下面是这个函数调用的原型: FILE *fopen( const char…...

模拟退火算法优化灰色
clc; clear; close all; warning off; %% tic T01000; % 初始温度 Tend1e-3; % 终止温度 L200; % 各温度下的迭代次数(链长) q0.9; %降温速率 X[16.4700 96.1000 16.4700 94.4400 20.0900 92.5400 22.3900 93.3700 25.…...
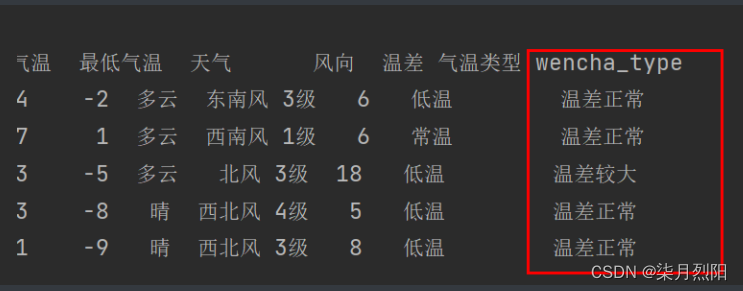
Pandas怎么添加数据列删除列
Pandas怎么添加数据列 1、直接赋值 # 1、直接赋值df.loc[:, "最高气温"] df["最高气温"].str.replace("℃", "").astype("int32")df.loc[:, "最低气温"] df["最低气温"].str.replace("℃"…...

C++类和对象:构造函数和析构函数
目录 一. 类的六个默认成员函数 二. 构造函数 2.1 什么是构造函数 2.2 编译器自动生成的默认构造函数 2.3 构造函数的特性总结 三. 析构函数 3.1 什么是析构函数 3.2 编译器自动生成的析构函数 3.3 析构函数的特性总结 一. 类的六个默认成员函数 对于任意一个C类&…...
【Stata】从入门到精通.零基础小白必学的教程,一学就fei
视频教程移步:https://www.bilibili.com/video/BV1hK4y1d714/?p4&spm_id_frompageDriver&vd_sourcecc8074e9c81a225f214226065db53d32P3 第二讲 Stata处理数据全流程(上) P3 - 01:37内置数据 file example datasets使用…...

【RuoYi优化】调整JVM启动内存
📔 笔记介绍 大家好,千寻简笔记是一套全部开源的企业开发问题记录,毫无保留给个人及企业免费使用,我是作者星辰,笔记内容整理并发布,内容有误请指出,笔记源码已开源,前往Gitee搜索《chihiro-notes》,感谢您的阅读和关注。 作者各大平台直链: GitHub | Gitee | CSD…...

[架构模型]MVC模型详细介绍,并应用到unity中
简介: MVC模式是一种软件架构模式,它将应用程序分为三个主要部分:模型(Model)、视图(View)和控制器(Controller)。MVC模式的目标是实现应用程序的松耦合,以便…...

?? JavaScript 双问号(空值合并运算符)
?? JavaScript 双问号(空值合并运算符) 一、简述 在网上浏览 JavaScript 代码时或者学习其他代码时,可能会发现有的表达式用了两个问号(??)如下所示: let username; console.log(username ?? "Guest"…...
作业2.25----通过操作Cortex-A7核,串口输入相应的命令,控制LED灯进行工作
1.通过操作Cortex-A7核,串口输入相应的命令,控制LED灯进行工作 例如在串口输入led1on,开饭led1灯点亮 2.例如在串口输入led1off,开饭led1灯熄灭 3.例如在串口输入led2on,开饭led2灯点亮 4.例如在串口输入led2off,开饭led2灯熄灭 5.例如在串口输入led…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
