当前位置：首页 > news >正文

线性代数第二章矩阵

news 2026/2/7 14:21:41

一、概念

$m\times n$ 个数排成的m行n列的表格

二、运算法则

三、初等变换

（1）用非零常数k乘矩阵的某一行（列）；

（2）互换矩阵某两行（列）的位置；

（3）把某行（列）的k倍加至另一行（列）。

称为矩阵的初等行（列）变换，统称初等变换。矩阵经初等行变换后秩不变。

初等矩阵：单位矩阵经过一次初等变换所得到的矩阵。用初等矩阵P左（右）乘矩阵A，其结果PA（AP）就是对矩阵A作一次相应的初等行（列）变换。初等矩阵均可逆，且其逆矩阵是同类型的初等矩阵，即

$E_{i}^{-1}(k)=E_{i}^{-1}(\frac{1}{k}),E_{ij}^{-1}(k)=E_{ij}^{-1}(-k),E_{ij}^{-1}=E_{ij}$

等价：矩阵A经过有限次初等变换变成矩阵B，则称矩阵A与矩阵B等价，记作 $A\cong B$ 。矩阵等价的充分必要条件是，存在可逆矩阵P与Q，使 $PAQ=B$ 。

四、特殊矩阵

转置矩阵：矩阵A的行换成同序数的列得到的一个新矩阵，记作 $A^T$

$(A^T)^T=A$

$(A+B)^T=A^T+B^T$

$(kA)^T=kA^T$

$(AB)^T=B^TA^T$

伴随矩阵：矩阵A的每个元素被其代数余子式所取代而构成的矩阵，记作 $A^*$ 。

对于二阶矩阵，主对角线元素互换，副对角线元素变号即可求出伴随矩阵。

$AA^*=A^*A=\left | A \right |E\Leftrightarrow A^*=\left | A\right |A^{-1}$

$\left | A^* \right |=\left | A \right |^{n-1}$

$(A^*)^{-1}=(A^{-1})^*=\frac{1}{\left | A \right |}A$

$(A^*)^T=(A^T)^*$

$(kA)^*=k^{n-1}A^*$

$(A^*)^*=\left | A \right |^{n-2}A$

$r(A^*)=\left\{\begin{matrix} n, \ if \ r(A)=n,\qquad \\ 1,\ if \ r(A)=n-1,\\ 0,\ if \ r(A)<n-1. \end{matrix}\right.$

可逆矩阵：存在n阶矩阵B $AB=BA=E$ （单位矩阵），则称A是可逆矩阵或非奇异矩阵，B是A的逆矩阵。

若n阶矩阵A可逆，则

$\left | A \right |\neq 0$
$r(A)=n$
A的列（行）向量组线性无关
$A=P_1P_{2}...P_s,P_i(i=1,2,...,s)$ 是初等矩阵
A与单位矩阵等价
0不是矩阵A的特征值

对称矩阵：满足 $A^T=A$

反对称矩阵：满足 $A^T=-A$

正交矩阵：满足 $AA^T=A^TA=E\Leftrightarrow A^{-1}=A^T$

对角矩阵

分块矩阵

五、计算逆矩阵

六、秩

秩r(A)=A的列秩=A的行秩

$r(A^T)=r(A)$

$r(A^TA)=r(A)$

$r(kA)=r(A)(k\neq 0)$

$r(A+B)\leqslant r(A)+r(B)$

$r(AB)\leqslant min(r(A),r(B))$

若A可逆，则 $r(AB)=r(BA)=r(B)$

若A列满秩，则 $r(AB)=r(B)$

若A是 $m\times n$ 矩阵，B是 $n\times s$ 矩阵， $AB=O$ ，则 $r(A)+r(B)\leqslant n$

$r\begin{bmatrix} A & O \\ O & B \end{bmatrix}=r(A)+r(B)$

若 $A\sim B$ ，则 $r(A)=r(B),r(A+kE)=r(B+kE)$

线性代数第二章矩阵

一、概念个数排成的m行n列的表格二、运算法则三、初等变换 （1）用非零常数k乘矩阵的某一行（列）； （2）互换矩阵某两行（列）的位置； （3&#…...

编程日记 2023/11/5 0:32:21

vue实现自定义字体

1、字体资源查找网址 https://eng.m.fontke.com/ 选择想要的字体之后下载获取文件夹内的.ttf文件 2 、字体引入在项目根目录下新建font文件夹，将ttf文件放在里面 3、相应的页面vue文件中引入在style标签中加上 font-face { font-family: ‘ZCOOLXiaoWei’…...

编程日记 2023/11/5 0:30:17

Selenium安装WebDriver Chrome驱动(含 116/117/118/119/120/)

1、确认浏览器的版本在浏览器的地址栏，输入chrome://version/，回车后即可查看到对应版本 2、找到对应的chromedriver版本 2.1 114及之前的版本可以通过点击下载chromedriver,根据版本号（只看大版本）下载对应文件 2.2 116版本…...

编程日记 2023/11/5 0:29:16

springboot的安全机制

一.jwt Spring Boot是一个用于开发Java应用程序的开源框架，它提供了一种快速、简单和可扩展的方式来构建独立的、生产级别的应用程序。在最新的版本Spring Boot 2.5中，引入了对JWT（JSON Web Token）的支持。本文将介绍如何在Spring Boot 2.5中使用JWT，并提供一个简单的示例…...

编程日记 2023/11/5 0:27:10

学习c++的第四天

目录运算符算术运算符关系运算符逻辑运算符位运算符赋值运算符杂项运算符运算符优先级运算符算术运算符算术运算符是 C 中用于执行基本算术操作的运算符。加法运算符 ()：将两个操作数相加。例如，A B 将得到 30，因为 …...

编程日记 2023/11/5 0:26:09

BIOS开发笔记 – 显示

UEFI启动流程跑完前三阶段，UEFI环境的准备基本完成，到BDS阶段的任务就是准备引导OS。在此之前还需要使一些必要的硬件工作起来，比如键盘设备，屏幕等，怎么让屏幕工作呢？简单的说就是执行其相关的UEFI驱动。要注意一下的是，这里所说的驱动并不是屏幕的驱动，而是GPU的驱动…...

编程日记 2023/11/5 0:25:08

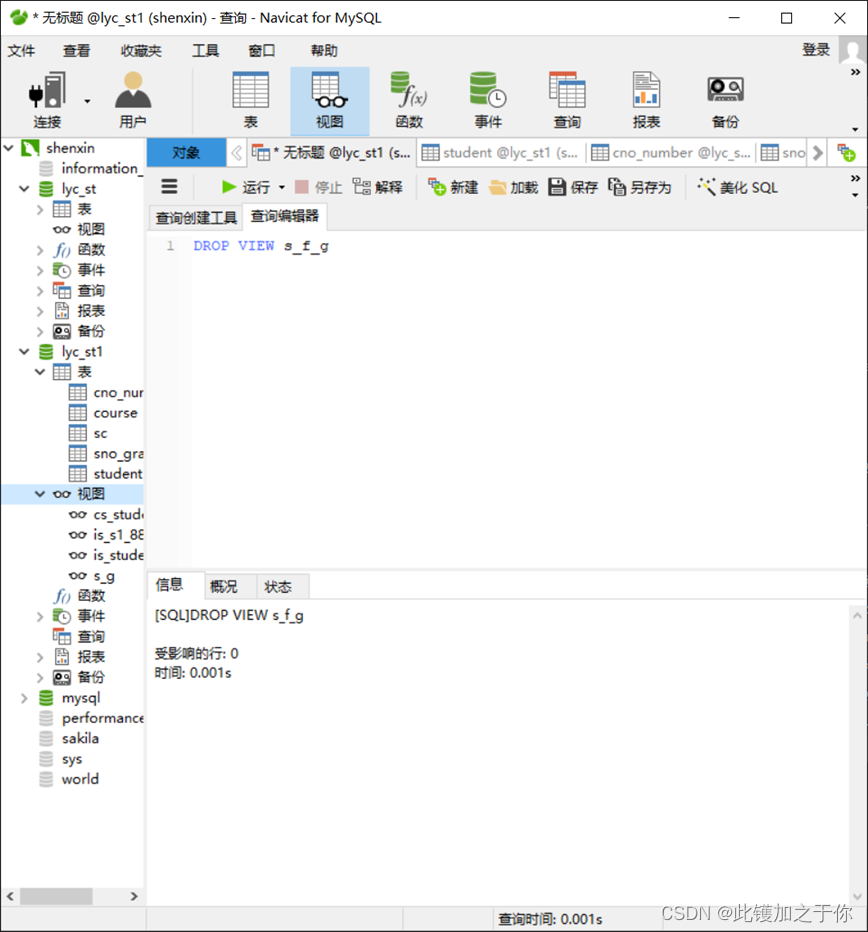
数据库实验：SQL的数据视图

目录视图概述视图的概念视图的作用实验目的实验内容实验要求实验过程视图概述视图是由数据库中的一个表或多个表导出的虚拟表，其作用是方便用户对数据的操作视图的概念视图是一个虚拟表，其内容由查询定义。同真实的表一样，视图包含一…...

编程日记 2023/11/5 0:24:08

k8s-调度约束

目录工作机制调度过程指定调度节点亲和性键值运算关系 Pod亲和性与反亲和性污点(Taint) 和容忍(Tolerations) 维护操作故障排除步骤 Kubernetes 是通过 List-Watch 的机制进行每个组件的协作，保持数据同步的，每个组件之间的设计实现了…...

编程日记 2023/11/5 0:23:07

C++设计模式_26_设计模式总结

本篇为C++设计模式的总结课，此篇再回到原帮助大家梳理一下。文章目录 1. 一个目标2. 两种手段3. 八大原则4. 重构技法5. 从封装变化角度对模式分类6. C++对象模型7. 关注变化点和稳定点8. 什么时候不用模式9. 经验之谈10. 设计模式成长之路1. 一个目标管理变化，提高复用！…...

编程日记 2023/11/5 0:22:06

解锁AI语言模型的秘密武器 - 提示工程

文章目录一、LLM概念1.1 什么是LLMs1.2 LLMs类别1.3 如何构建LLM 二、提示工程简介2.1 基础提示2.2 使用提示词的必要性三、提示3.1 如何写好提示词3.1.1 使用分隔符3.1.2 结构化输出3.1.3 风格信息3.1.4 给定条件3.1.5 给出示例3.1.6 步骤分解3.1.7 不断迭代 3.2 提示工程3…...

编程日记 2023/11/5 0:21:05

qt手撕菜单栏

最近有个项目需要手写菜单栏。就写了一个简单的程序，供大家参考！ #include <QApplication> #include <QMainWindow> #include <QMenuBar> #include <QMenu> #include...

编程日记 2023/11/5 0:20:03

UE5——网络——RPC

RPC（这个是官方文档的资料） 要将一个函数声明为 RPC，您只需将 Server、Client 或 NetMulticast 关键字添加到 UFUNCTION 声明。例如，若要将某个函数声明为一个要在服务器上调用、但需要在客户端上执行的 RPC，您可以…...

编程日记 2023/11/5 0:17:59

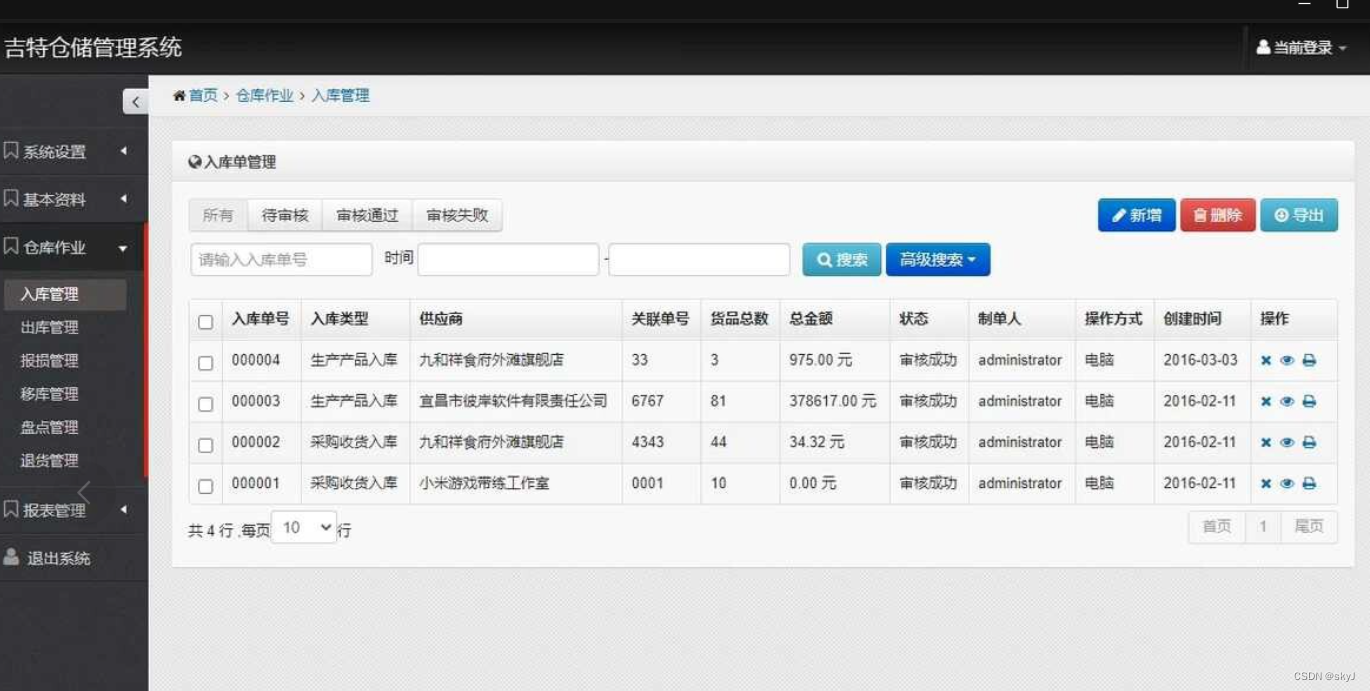
基于ASP.NET MVC + Bootstrap的仓库管理系统

基于ASP.NET MVC Bootstrap的仓库管理系统。源码亲测可用，含有简单的说明文档。适合单仓库，基本的仓库入库管理，出库管理，盘点，报损，移库，库位等管理，有着可视化图表。系统采用Bo…...

编程日记 2023/11/5 0:16:57

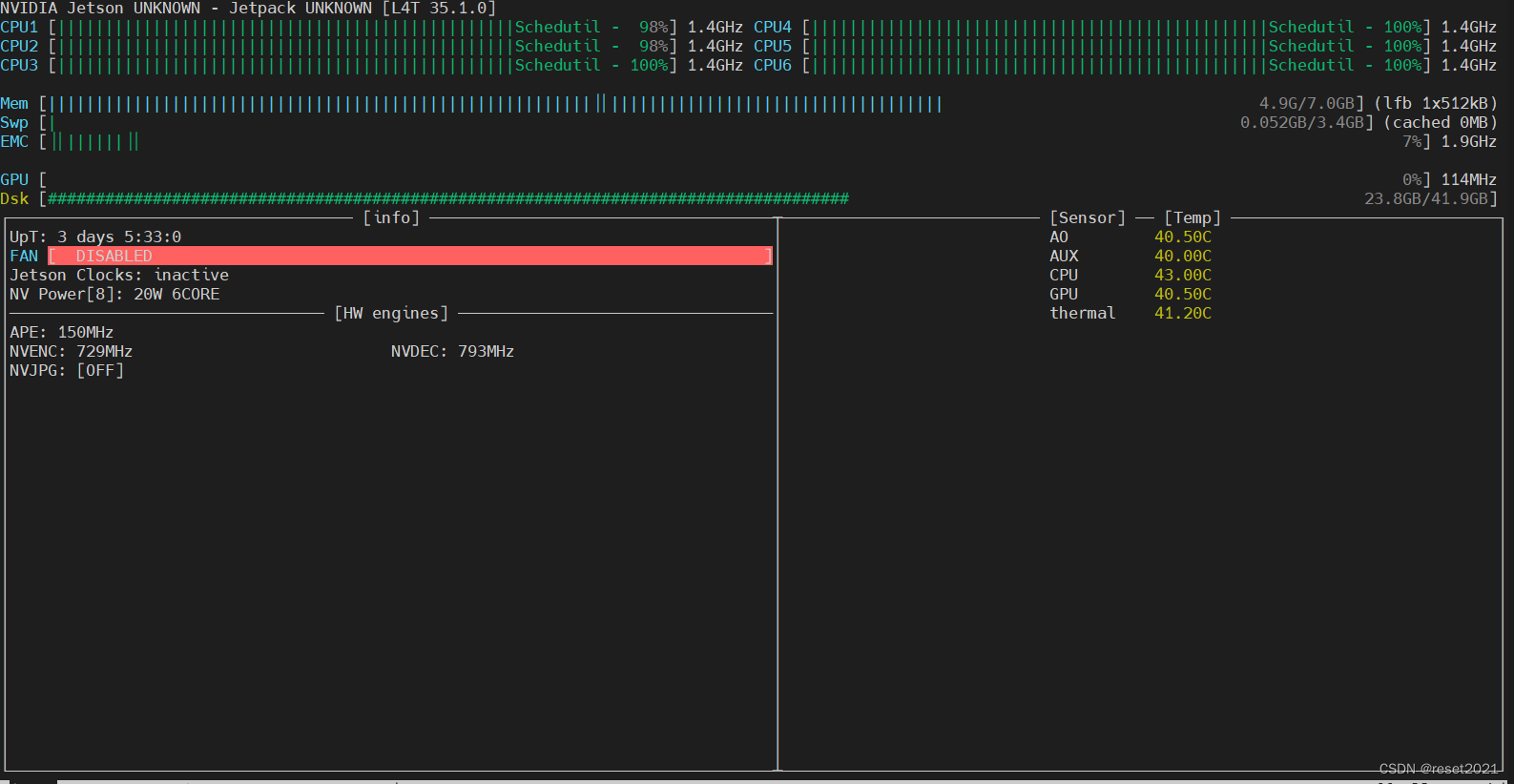
Jetson NX FFmpeg硬件编解码实现

最近在用Jetson Xavier NX板子做视频处理，但是CPU进行视频编解码，效率比较地下。于是便考虑用硬解码来对视频进行处理。通过jtop查看，发现板子是支持 NVENC硬件编解码的。 1、下载源码因为需要对ffmpeg进行打补丁修改，因此需…...

编程日记 2023/11/5 0:15:56

5.2用队列实现栈（LC225-E）

算法： 其实这道题不用像上一道题一样，用两个队列实现栈。由于队列的数据结构特性。用一个队列就可实现栈。难点还是在出队的时候： 比如队列[1,2,3]，要模拟一个栈入栈就是直接append（其实就是C中的push&#xff0…...

编程日记 2023/11/5 0:14:54

项目上线前发现严重Bug怎么办？

今天分享一个面试问题，现在有一个面试场景： 项目计划明天发布，但是在今天你作为测试人员发现了一个严重的bug，市场相关人员又在催发布的事情，这个时候你应该怎么办？ 这是测试工程师不管是在面试&#xff0…...

编程日记 2023/11/5 0:13:53

【WPF系列】- Application详解

【WPF系列】- Application详解文章目录【WPF系列】- Application详解一、Application简介Application 类具体有以下功能: 二、初始App.xaml二、自定义Main方法启动WPF应用程序第一种：启动应用程序的代码第二种：启动应用程序的代码第三种：启…...

编程日记 2023/11/5 0:12:53

常见的内置方法：call,getitem,iter,next

1.__call__方法在创建好一个实例后，直接调用一个实例会报错。但使用__call__后，可以让这个实例可以像方法一样被调用（就是一个函数后面加个括号的函数调用形式） class Person:passp1 Person() p1() # 实例这样无法直接被调…...

编程日记 2023/11/5 0:11:52

python用cv2画图（line, rectangle, text等）

Python做图像图形研究的时候，通常需要画很多辅助几何形状（比如bounding box等）。基于opencv的几何图形绘制具有易用性，而且天然能和numpy数组交互。本文总结了几种常用的cv2画几何图形的方法，当一个简易的手册使用&a…...

编程日记 2023/11/5 0:10:51

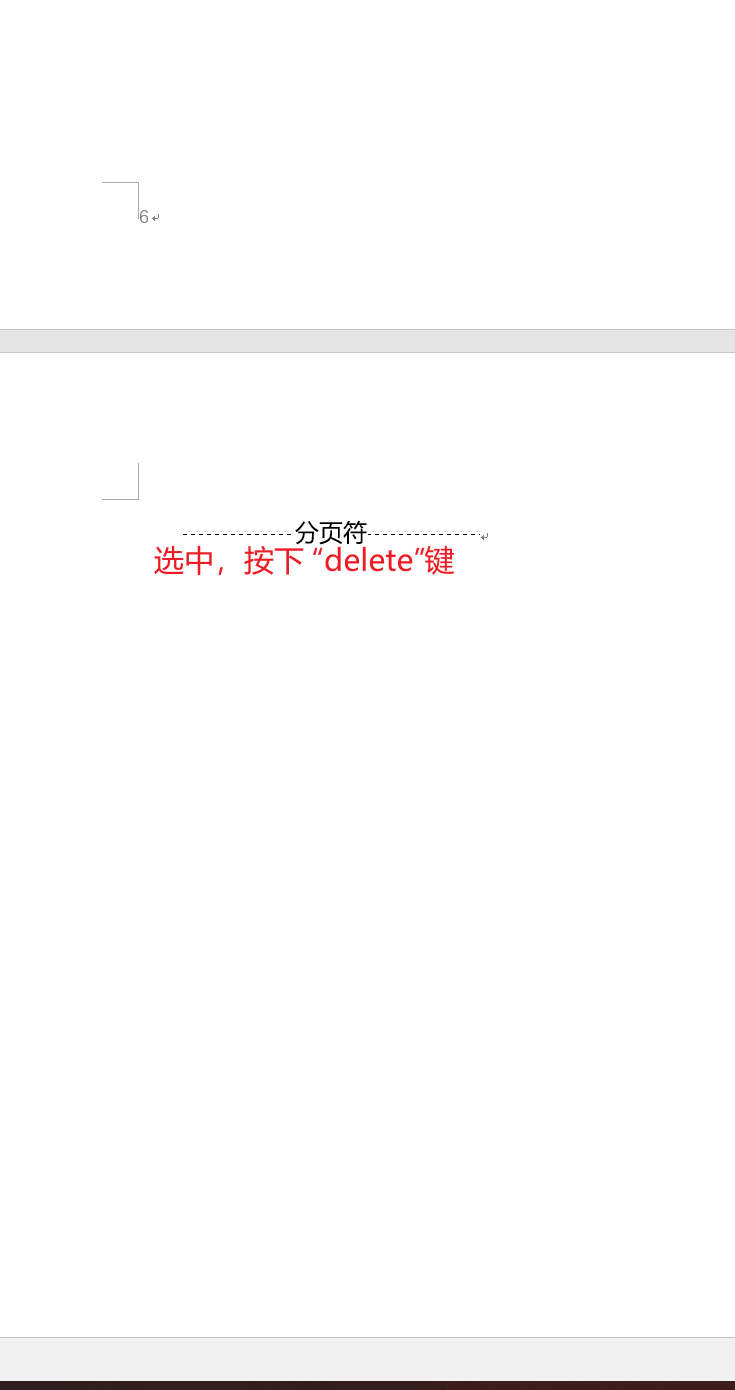
解决方案中word中分页符的使用

在投标方案中要善于使用“分页符”，尽可能少使用分节符号，没有分页符前，你每次修改你的标书或者文件，增加或者修改内容后。你的格式字段前后都是会发生变化，如何稳定的保证结构呢，那就是分页符的使用&#…...

编程日记 2023/11/5 0:09:50

Chapter03-Authentication vulnerabilities

文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

编程新知 2026/2/7 4:57:53

Appium+python自动化（十六）- ADB命令

简介 Android 调试桥(adb)是多种用途的工具，该工具可以帮助你你管理设备或模拟器的状态。 adb ( Android Debug Bridge)是一个通用命令行工具，其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利，如安装和调试…...

编程新知 2026/1/21 18:20:51

招商蛇口 | 执笔CID，启幕低密生活新境

作为中国城市生长的力量，招商蛇口以“美好生活承载者”为使命，深耕全球111座城市，以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子，招商蛇口始终与城市发展同频共振，以建筑诠释对土地与生活的…...

编程新知 2026/1/26 8:13:33

AI+无人机如何守护濒危物种？YOLOv8实现95%精准识别

【导读】野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而，传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案，能够实现大范围覆盖并远程采集数据。尽管具备这些优势&#xf…...

编程新知 2026/1/26 12:50:00

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表

设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程，两张表是相同的结构，都有整型主键id字段，需要每次从数据库分批取得2000条数据，用于比较，比较操作的同时可以再取2000条数据，等上一次比较完成之后，开始比较，直到比较完所有的数据。比较操作需要比较…...

编程新知 2025/9/14 5:35:46

脑机新手指南（七）：OpenBCI_GUI：从环境搭建到数据可视化（上）

一、OpenBCI_GUI 项目概述 （一）项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台，其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言，首次接触 OpenBCI 设备时，往…...

编程新知 2026/2/3 4:26:32

论文阅读：Matting by Generation

今天介绍一篇关于 matting 抠图的文章，抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法，已经有很多的工作和这个任务相关。这两年 diffusion 模型很火，大家又开始用 diffusion 模型做各种 CV 任务了&am…...

编程新知 2026/1/27 19:36:39

实战设计模式之模板方法模式

概述模板方法模式定义了一个操作中的算法骨架，并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下，重新定义算法中的某些步骤。简单来说，就是在一个方法中定义了要执行的步骤顺序或算法框架，但允许子类…...

编程新知 2026/1/26 23:42:12

云安全与网络安全：核心区别与协同作用解析

在数字化转型的浪潮中，云安全与网络安全作为信息安全的两大支柱，常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异，并探讨它们的协同作用。一、核心区别定义与范围网络安全：聚焦于保…...

编程新知 2026/1/28 22:45:10

Monorepo架构: Nx Cloud 扩展能力与缓存加速

借助 Nx Cloud 实现项目协同与加速构建 1 ） 缓存工作原理分析在了解了本地缓存和远程缓存之后，我们来探究缓存是如何工作的。以计算文件的哈希串为例，若后续运行任务时文件哈希串未变，系统会直接使用对应的输出和制品文件。 2 …...

编程新知 2025/12/15 8:20:48

一、概念

二、运算法则

三、初等变换

四、特殊矩阵

五、计算逆矩阵

六、秩

相关文章：