暴力递归转动态规划(十三)
题目
给定3个参数,N,M,K
怪兽有N滴血,等着英雄来砍自己
英雄每一次打击,都会让怪兽流失[0~M]的血量
到底流失多少?每一次在[0~M]上等概率的获得一个值
求K次打击之后,英雄把怪兽砍死的概率。
暴力递归
先确定好暴力递归的尝试方法,并根据方法确定base case。
已知参数是 N:怪兽血量 M:每次等概率砍0 ~ M滴血 K:砍K次。
所以如果暴力递归方法返回在hp滴血情况下,砍times次,每次砍0 ~ M滴血。能将怪兽砍死的方法数。
其中hp:剩余血量 。 tmies:剩余砍的次数。M固定不变。
代码
递归方法就如上面所描述的递归方法进行的尝试,每次砍都等概率掉 0 ~ M滴血(for循环表示),每次掉血后,继续相加递归(次数 times - 1, hp - i 为剩余血量),砍当前砍掉 i 滴血后,能砍死怪兽的方法。
base case : 当次数为0时,如果hp <= 0 ,则return 1,证明怪兽gg,否则返回0,证明当前情况下没砍死怪兽。
需要注意的是,times不为0,但是怪兽 hp <= 0 的情况。
比如说:怪兽hp = 3 。times = 4 还可砍击4次,每次掉 0 ~ 5滴血。
可能我第一刀的时候就砍了5滴血。剩下的3次无论怎么砍,都会成功,怪兽都已经是GG的状态。
此时,就运用到了之前我们所说的“剪枝”的优化技巧。
剩下的几刀都没有必要再进行递归方法向下调用。但是每次 0 ~ M滴血,就是一个M + 1的展开情况,剩余 times = 3。
直接可求得剩余击杀怪兽的方法数 = Math.pow(M + 1, times);
public static double right(int N, int M, int K) {if (N < 1 || M < 1 || K < 1) {return 0;}//砍怪兽的总方法数:每次都是 0 ~ M滴血,所以是 M + 1的展开,能砍K次。double all = Math.pow(M + 1, K);//击杀怪兽的方法数。double kill = (double) process(K, M, N);return kill / all;}public static double process(int times, int M, int hp) {//如果剩余次数为0,此时剩余血量 <= 0,代表把怪兽砍死,return 1,否则return 0if (times == 0) {return hp <= 0 ? 1 : 0;}//如果在次数用没之前就已经将怪兽砍死,那么直接returnif (hp <= 0) {return Math.pow(M + 1, times);}int ways = 0;//否则,等概率的砍,每一刀砍的范围 0 ~ M。每砍一刀,次数 - 1。for (int i = 0; i <= M; i++) {ways += process(times - 1, M, hp - i);}return ways;}
动态规划
根据上面暴力递归的代码可以看出,可变参数为 hp:怪兽剩余血量 。 times:剩余砍击次数。又因为hp和times都可以到达0。所以可以确定dp表是一个二维数组,以及范围是dp[K + 1][N + 1]。(K,N为题意所给的血量和次数)。
根据暴力递归的base case,当次数为0时,hp如果为0,则return 1。所以可以确定dp[0][0] = 1
if (times == 0) {return hp <= 0 ? 1 : 0;}
根据这行base case,也可以确定,dp[0][hp] = Math.pow(M + 1, times);。
if (hp <= 0) {return Math.pow(M + 1, times);
}
其余代码照搬暴力递归即可。
完整代码
遍历过程中,hp会有负数的可能,需要注意并进行判断。因为dp表大小是dp[K + 1][N + 1],此时如果要考虑负数的因素就要扩大N + 1的返回,增加判断,很麻烦。
所以要对hp - i 进行判断, 如果 hp - i >= 0 则从dp表中取。如果 hp - i < 0。则直接从我们的公式 Math.pow(M + 1, times - 1);中取,times - 1是因为当前第times次砍击砍下来后hp - i < 0,剩余times - 1次肯定就是成功的情况。
public static double dp(int N, int M, int K) {if (N < 1 || M < 1 || K < 1) {return 0;}double all = Math.pow(M + 1, K);int[][] dp = new int[K + 1][N + 1];dp[0][0] = 1;for (int times = 1; times <= K; times++) {dp[times][0] = (int) Math.pow(M + 1, times);for (int hp = 1; hp <= N; hp++) {int ways = 0;for (int i = 0; i <= M; i++) {if (hp - i >= 0) {ways += dp[times - 1][hp - i];} else {ways += (int) Math.pow(M + 1, times - 1);}}dp[times][hp] = ways;}}return (double)((double)dp[K][N] / (double)all);}
再次优化
可以看到,动态规划的过程中出现了枚举行为(for循环 0 ~ M滴血),所以如果找到dp表中每个格子间的依赖关系,那么还有进一步的优化空间。
以下图为例:假设,当前times = 2 还剩2次机会,hp = 3 剩余3滴血,M = 3 每次等概率掉 0 ~ 3滴血。
根据暴力递归中依赖关系是 times - 1,hp - i ,i = 0 ~ 3,所以想要求得dp[2][3]格子 √ 处的值需要依赖dp[1,0] ~ dp[1,4]四个格子的累加。
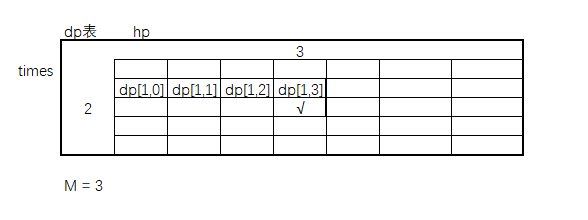
求√’处的值,hp = 4,依然是剩余2次机会,每次 0 ~ 3,依赖的就是dp[1,1] ~ dp[1][4]的值,那此时如果用 √ + dp[1][4] - dp[1][0],是不是就省去了再求dp[1][1] ~ dp[1][3]的过程。
我们将此过程抽象化一下,就是优化后的代码。

优化代码
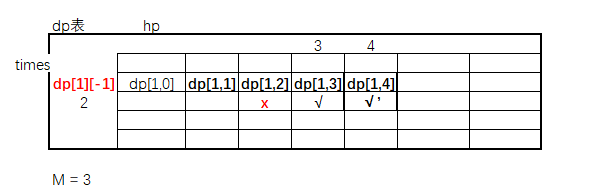
同样要考虑hp负数的问题,如果hp为负数,则前面的也要减掉。
如图:求 √ 位置时,依赖的X已经越界了,那么此时,利用公式Math.pow(M + 1, times - 1);减掉前面的位置。
public static double bestDP(int N, int M, int K) {if (N < 1 || M < 1 || K < 1) {return 0;}double all = Math.pow(M + 1, K);int[][] dp = new int[K + 1][N + 1];dp[0][0] = 1;for (int times = 1; times <= K; times++) {dp[times][0] = (int) Math.pow(M + 1, times);for (int hp = 1; hp <= N; hp++) {dp[times][hp] = dp[times][hp - 1] + dp[times - 1][hp];if (hp - M - 1 <= 0) {dp[times][hp] -= Math.pow(M + 1, times - 1);} else {dp[times][hp] -= dp[times - 1][hp - M - 1];}}}return (double) ((double) (dp[K][N]) / all);}
相关文章:

暴力递归转动态规划(十三)
题目 给定3个参数,N,M,K 怪兽有N滴血,等着英雄来砍自己 英雄每一次打击,都会让怪兽流失[0~M]的血量 到底流失多少?每一次在[0~M]上等概率的获得一个值 求K次打击之后,英雄把怪兽砍死的概率。 暴…...
java EE 进阶
java EE 主要是学框架(框架的使用,框架的原理) 框架可以说是实现了部分功能的半成品,还没装修的毛坯房,然后我们再自己打造成自己喜欢的成品 这里学习四个框架 : Spring ,Spring Boot, Spring MVC, Mybatis JavaEE 一定要多练习,才能学好 Maven 目前我们主要用的两个功能: …...

记录paddlepaddle-gpu安装
背景 由于最近需要使用paddleocr,因此需要安装依赖paddlepaddle-gpu,不管怎么安装cuda11.6-11.8安装了一遍,都无法正常安装成功。如下所示: 环境:wsl2linux18.04 >>> import paddle >>> paddle.u…...

django如何连接sqlite数据库?
目录 一、SQLite数据库简介 二、Django连接SQLite数据库 1、配置数据库 2、创建数据库表 三、使用Django ORM操作SQLite数据库 1、定义模型 2、创建对象 3、查询对象 总结 本文将深入探讨如何在Django框架中连接和使用SQLite数据库。我们将介绍SQLite数据库的特点&…...
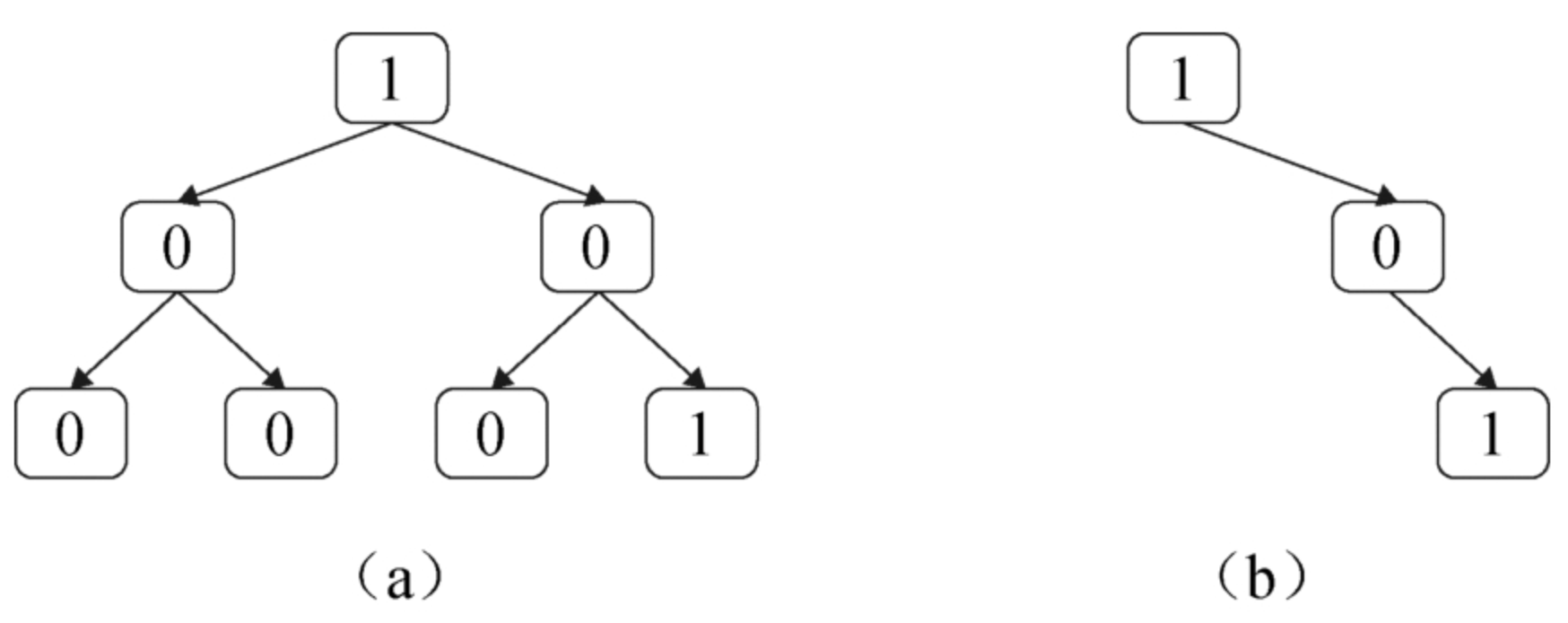
面试算法47:二叉树剪枝
题目 一棵二叉树的所有节点的值要么是0要么是1,请剪除该二叉树中所有节点的值全都是0的子树。例如,在剪除图8.2(a)中二叉树中所有节点值都为0的子树之后的结果如图8.2(b)所示。 分析 下面总结什么样的节…...
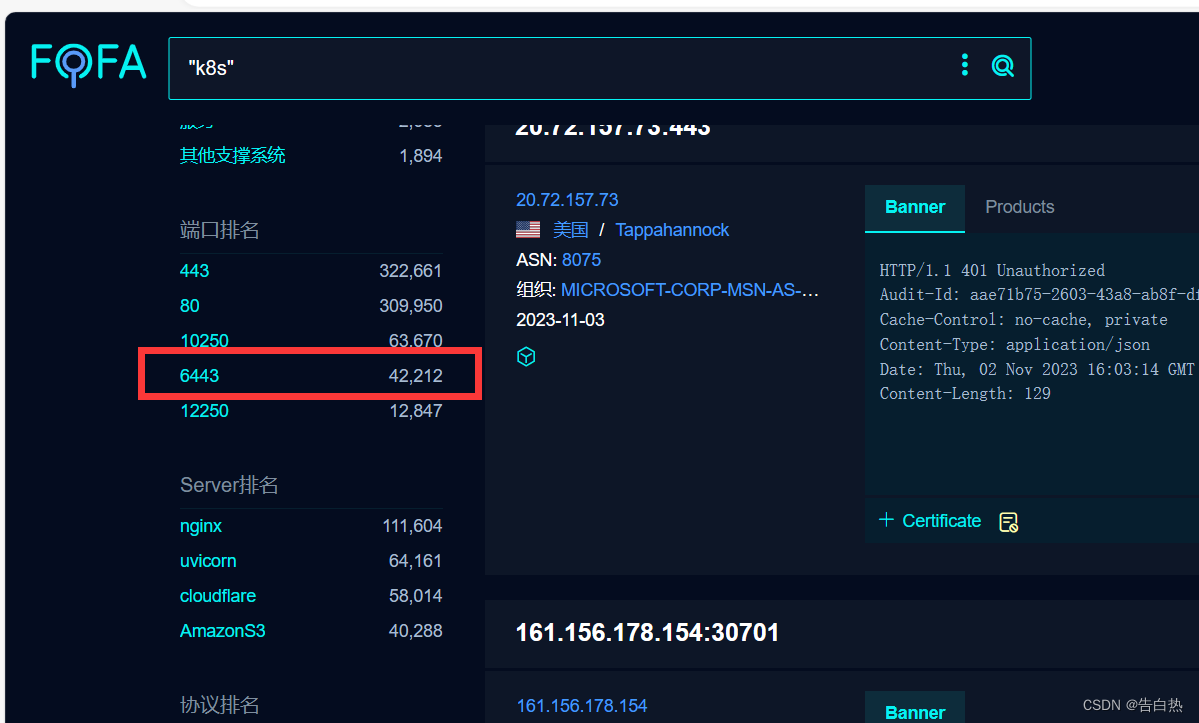
云安全-云原生k8s攻击点(8080,6443,10250未授权攻击点)
0x00 k8s简介 k8s(Kubernetes) 是容器管理平台,用来管理容器化的应用,提供快速的容器调度、弹性伸缩等诸多功能,可以理解为容器云,不涉及到业务层面的开发。只要你的应用可以实现容器化,就可以部…...

性能压力测试主要目标及步骤
性能压力测试是软件开发生命周期中至关重要的一部分,旨在评估应用程序或系统在高负载和极端条件下的性能表现。这种测试有助于发现性能瓶颈、资源耗尽和错误,以确保应用程序在真实使用情况下的可靠性和稳定性。本文将探讨性能压力测试的概念、方法和最佳…...
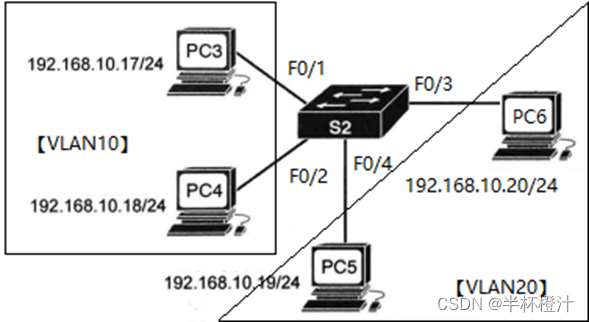
VLAN与配置
VLAN与配置 什么是VLAN 以最简单的形式为例。如下图,此时有4台主机处于同一局域网中,很明显这4台主机是能够直接通讯。但此时我需要让处于同一局域网中的PC3和PC4能通讯,PC5和PC6能通讯,并且PC3和PC4不能与PC5和PC6通讯。 为了实…...
API接口安全设计
简介 HTTP接口是互联网各系统之间对接的重要方式之一,使用HTTP接口开发和调用都很方便,也是被大量采用的方式,它可以让不同系统之间实现数据的交换和共享。 由于HTTP接口开放在互联网上,所以我们就需要有一定的安全措施来保证接口…...

服务器的管理口和业务口
服务器管理接口和业务接口 服务器管理接口(Server Management Interface,SMI): 服务器管理接口是一种用于管理服务器硬件和操作系统的标准接口。它通常用于远程管理和监控服务器,包括但不限于以下功能: …...

【gpt redis】原理篇
用的黑马程序员redis课程的目录,但是不想听讲了。后续都是用gpt文档获取的。 1.课程介绍(Av766995956,P145) 2.Redis数据结构-动态字符串(Av766995956,P146) sds 1M是个界限 其实他是个由c语言实现的结构体 有这么几个参数 len alloc flag char[] len是实际长度 …...

python二次开发Solidworks:排雷以及如何排雷?
目录 1、重要文档 2、MSDN VARIANTS 3、错误排除实例 3.1 第一个例子 3.2 第二个例子 1、重要文档 SolidWorks API 帮助文档:在 SolidWorks 的安装路径下可以找到本地文件,如 ...\Program Files\SolidWorks Corp\SolidWorks\api\apihelp.chm 。 s…...
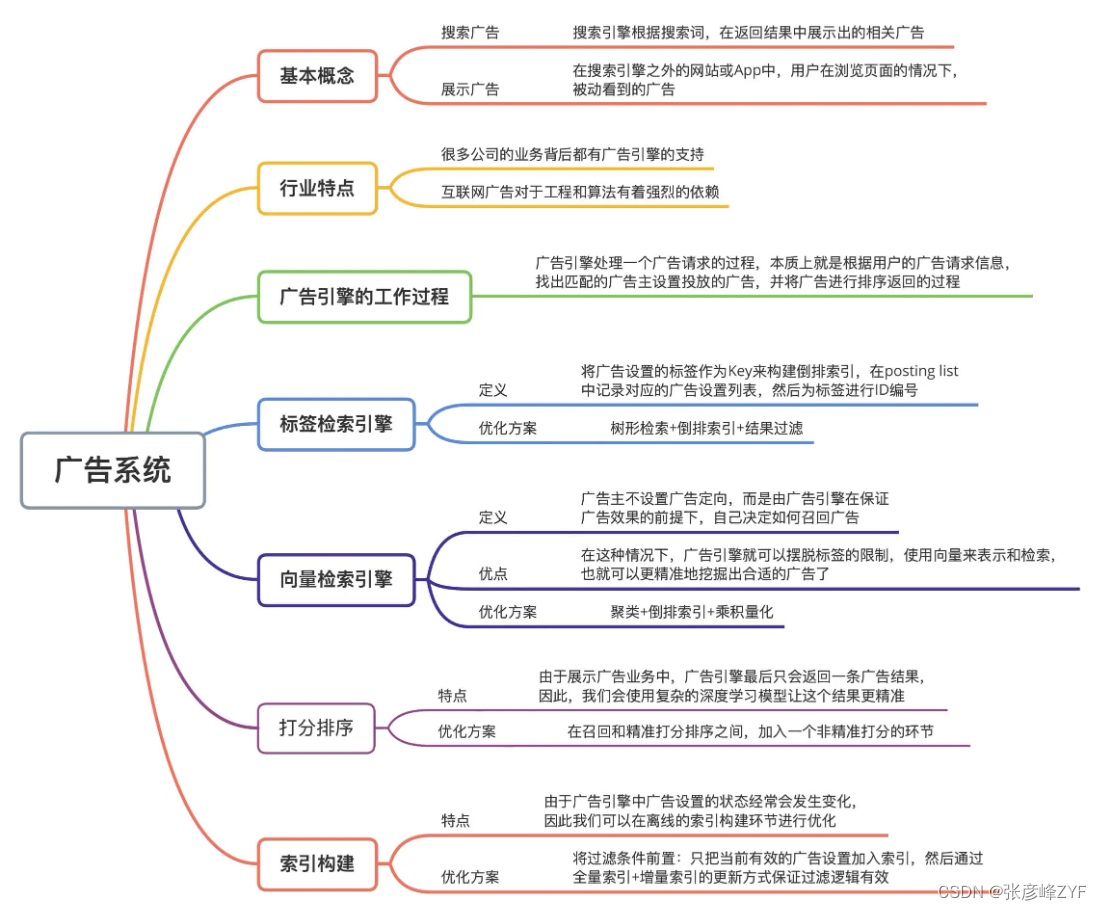
广告引擎检索技术快速学习
目录 一、广告系统与广告引擎介绍 (一)广告系统与广告粗分 (二)广告引擎在广告系统中的重要性分析 二、广告引擎整体架构和工作过程 (一)一般概述 (二)核心功能架构图 三、标…...

Scala的类和对象
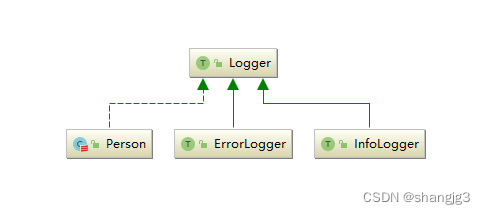
1. 初识类和对象 Scala 的类与 Java 的类具有非常多的相似性,示例如下: // 1. 在 scala 中,类不需要用 public 声明,所有的类都具有公共的可见性 class Person {// 2. 声明私有变量,用 var 修饰的变量默认拥有 getter/setter 属性private var…...
运算符只会匹配那些具有非空值的记录)
SQL中 <>(不等于)运算符只会匹配那些具有非空值的记录
0. 场景 idflag112null3 一张表的有有个varchar类型的flag字段,字段值有 null值/空值和 1。 flag为 1即表示逻辑删除,我想找出flag字段非 1 的所有情况: 一开始sql写法: select * from table where flag<>‘1’理想情况,结果集应该有2条记录(id为 2 和 3 的记录)实际情…...
)
冒泡排序(Java)
基本思想 比较前后相邻的二个数据,如果前面数据大于后面的数据,就将这二个数据交换。这样对数组的第 0 个数据到 N-1 个数据进行一次遍历后,最大的一个数据就“沉”到数组第N-1 个位置。如此循环 (N-1)次,每次循环需要比较的个数…...

k8s集群调度
目录 1、理论: 1.1、 概述: 1.2、Pod 是 Kubernetes 的基础单元,Pod 启动典型创建过程如下: 工作机制 **** 1.3、调度过程 *** 1.4、Predicate 有一系列的常见的算法可以使用: ** 1.5、 优先级由一系列键…...
Scala中类的继承、抽象类和特质
1. 类的继承 1.1 Scala中的继承结构 Scala 中继承关系如下图: Any 是整个继承关系的根节点; AnyRef 包含 Scala Classes 和 Java Classes,等价于 Java 中的 java.lang.Object; AnyVal 是所有值类型的一个标记; Nul…...

小程序如何实现登录数据持久化
在小程序中实现登录数据的持久化可以通过以下几种方式: 使用本地缓存 在用户登录成功后,将登录凭证或用户信息等数据使用 wx.setStorageSync 方法存储到本地缓存中: // 存储登录数据到本地缓存 wx.setStorageSync(token, 登录凭证); wx.set…...
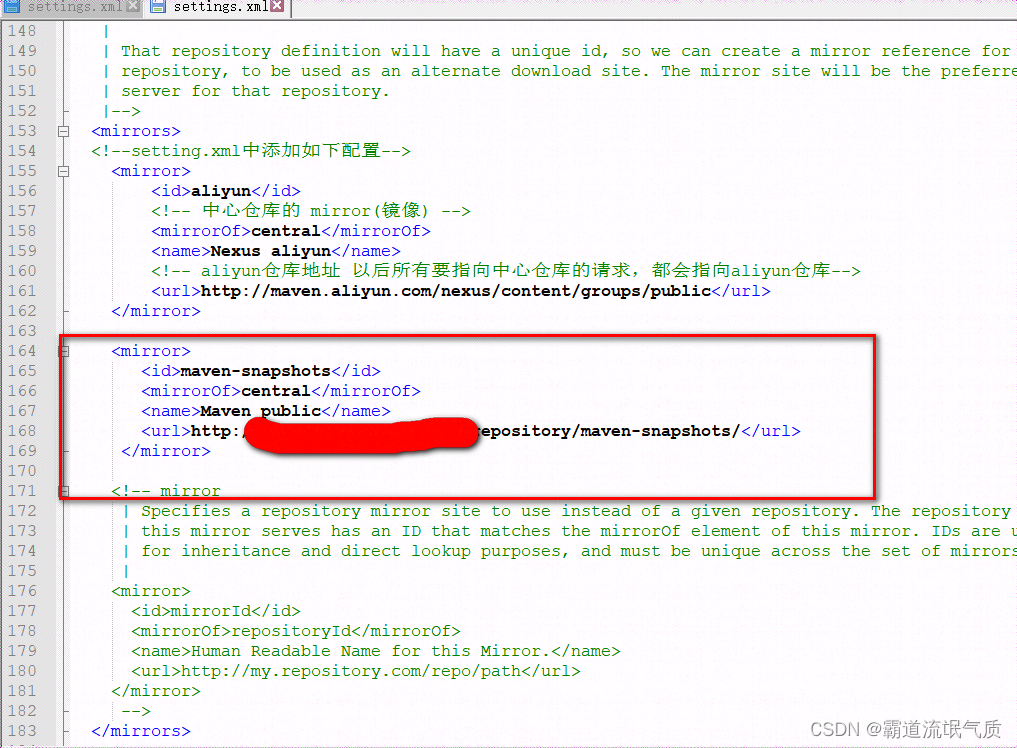
Maven本地配置获取nexus私服的依赖
场景 Nexus-在项目中使用Maven私服,Deploy到私服、上传第三方jar包、在项目中使用私服jar包: Nexus-在项目中使用Maven私服,Deploy到私服、上传第三方jar包、在项目中使用私服jar包_nexus maven-releases 允许deploy-CSDN博客 在上面讲的是…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
