快速排序(Java)
基本思想
快速排序Quicksort)是对冒泡排序的一种改进。 基本思想是分治的思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序算法的平均时间复杂度是 O(nlogn)
快速排序法示意图:
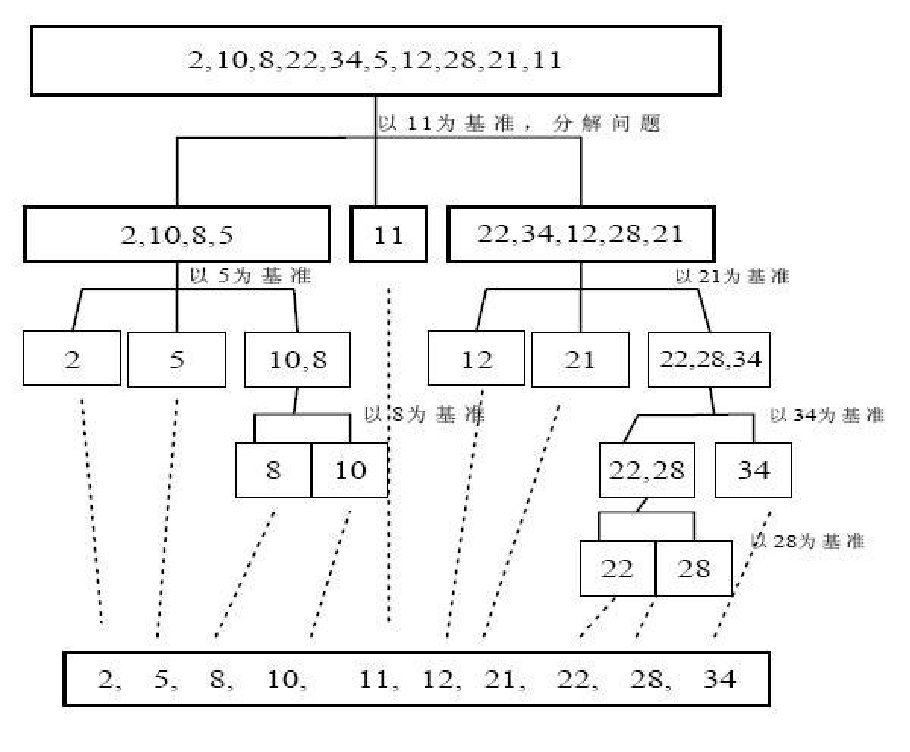
代码实现
思路:**左右双指针移动 **
例(从小到大排序下面的数组元素)

-
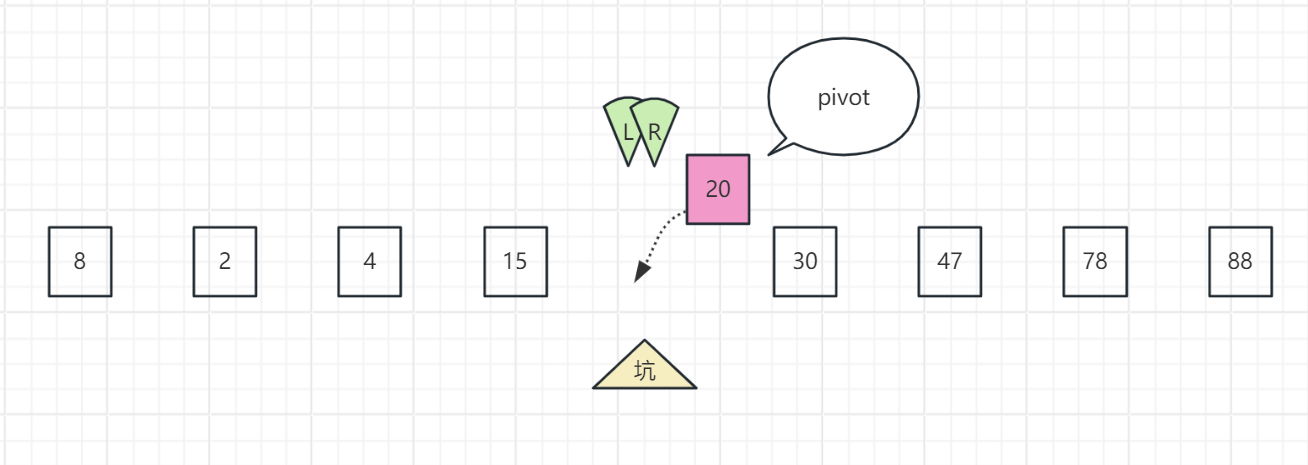
选择最右侧数值作为基准(pivot),并将该位置作为坑;左指针(left)指向最左侧数字,右指针(right)指向最右侧数字
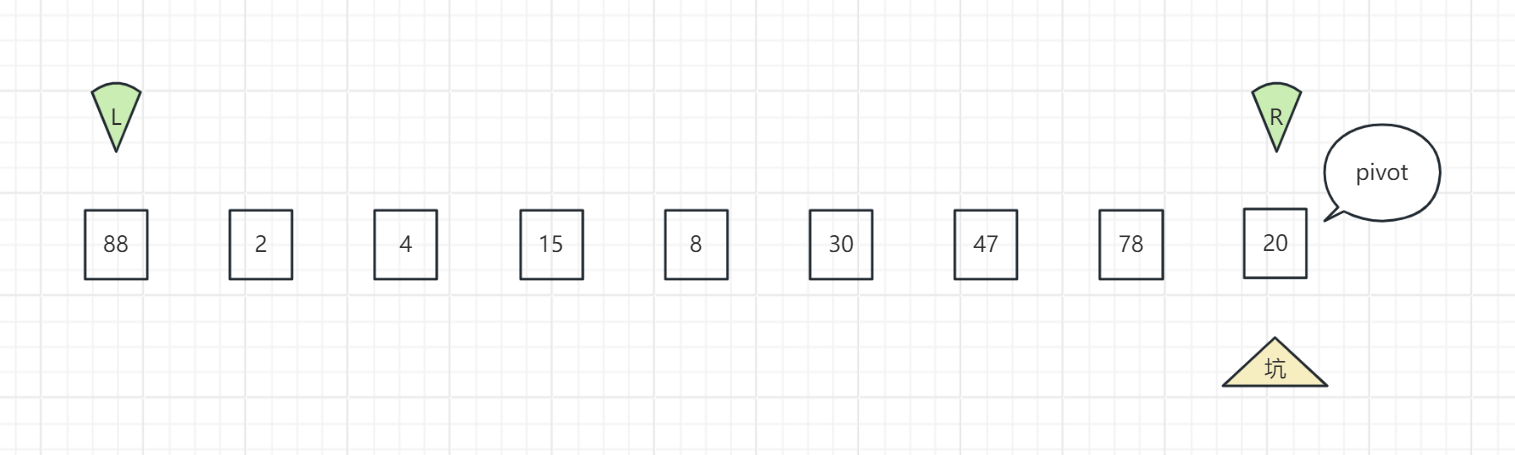
-
左指针向右移动。当左指针与右指针相遇(指向同一数字)时停下来,或者左指针指向数字大于pivot时也停下来,将该值填入坑中,将坑改为此位置
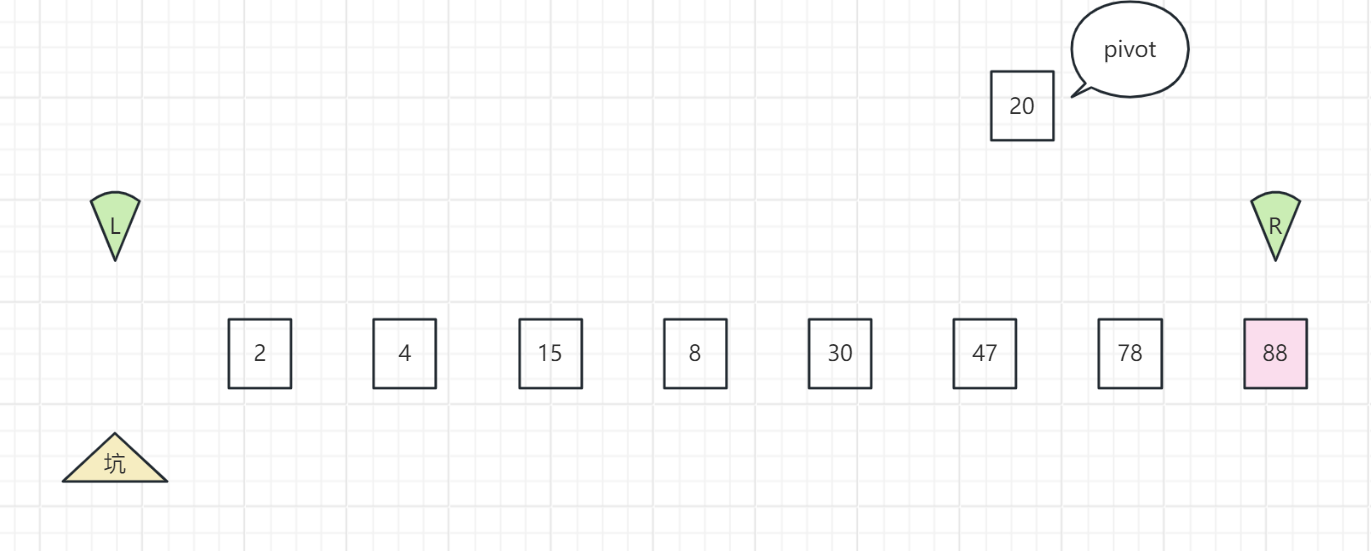
-
右指针向左移动。左指针与右指针相遇时停下来,或者右指针指向数字小于pivot时也停下来,将该值填入坑中,将坑改为此位置
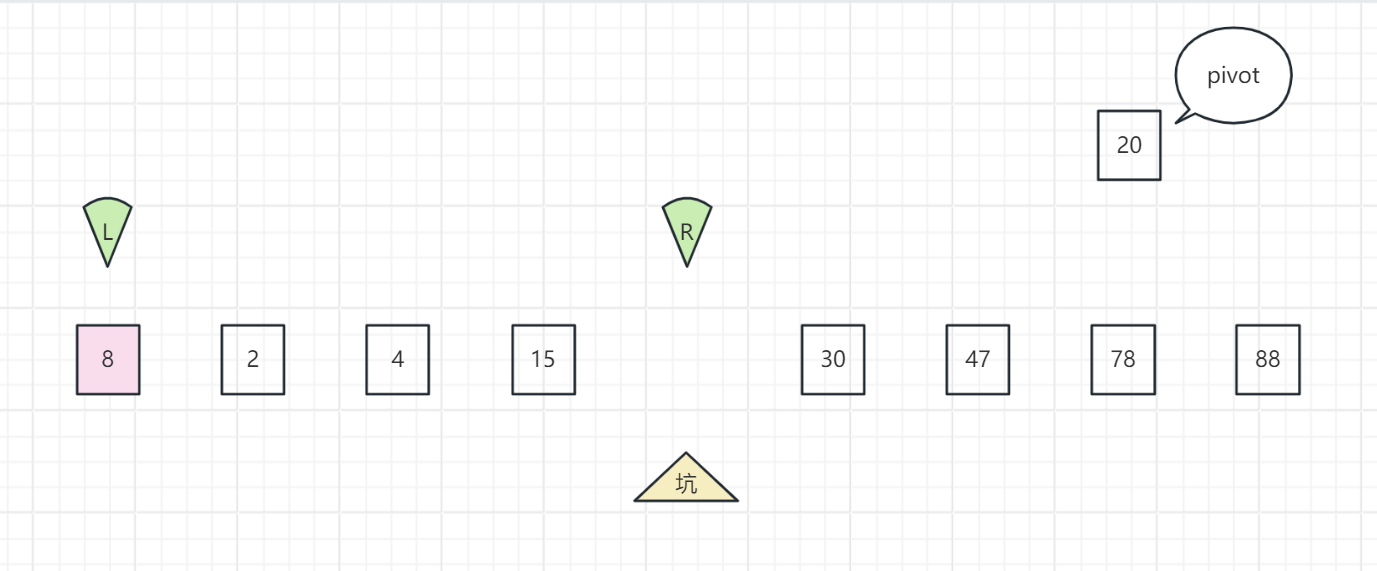
-
循环2、3步直至两指针相遇。如果此时左指针与右指针相遇,此时该位置为坑,将pivot填入该坑中,这样pivot的位置就找好了。
-
递归(以上步骤)基准左、右两旁的数列,直至数列不可再分则完成排序
备注:
- 递归的出口必须仔细考虑清楚,否则就会陷入无穷循环从而使栈溢出;
- 这里如果pivot 选在左侧,就要先从右侧开始遍历,反之则先从左侧开始
- 记得考虑到数值相同的情况
代码落地
public static void quickSort(int[] arr,int startIndex, int endIndex) {if (startIndex >= endIndex) {return;}int left = startIndex, right = endIndex, pivot = arr[endIndex];while (left < right) {while (left < right && arr[left] <= pivot) {left++;}arr[right] = arr[left];while (left < right && arr[right] >= pivot) {right--;}arr[left] = arr[right];}arr[left] = pivot;quickSort(arr, startIndex, left - 1);quickSort(arr, left + 1, endIndex);
}
参考文章
快速排序法(详解)
五分钟学会一个高难度算法:快速排序
排序算法之快速排序(Java实现)
相关文章:

快速排序(Java)
基本思想 快速排序Quicksort)是对冒泡排序的一种改进。 基本思想是分治的思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排…...

在ffmpeg中,如何把h264转换为rgb格式
在ffmpeg中,网络视频流h264为什么默认的转为YUV而不是其他格式 文章中介绍了,h264解码的时候是直接解码为yuv的,如果在使用的过程中 需要用到rgb的格式,我们该如何来转换这种格式呢? 在上面的文章中,我们已…...

【重磅】Cookies、headers、Session规律总结,搞定卡点
【重磅】Cookies规律总结,搞定卡点 登录后开始正式获取数据阶段: 不使用session: 放在请求头headers中 当如是:headers = {“user-agent”: “Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/104.0.0.0 Safari/537.36”,“Coo…...
【雷达原理】雷达杂波抑制方法
目录 一、杂波及其特点 1.1 什么是杂波? 1.2 杂波的频谱特性 二、动目标显示(MTI)技术 2.1 对消原理 2.2 数字对消器设计 三、MATLAB仿真 3.1 对消效果验证 3.2 代码 一、杂波及其特点 1.1 什么是杂波? 杂波是相对目标回波而言的,…...
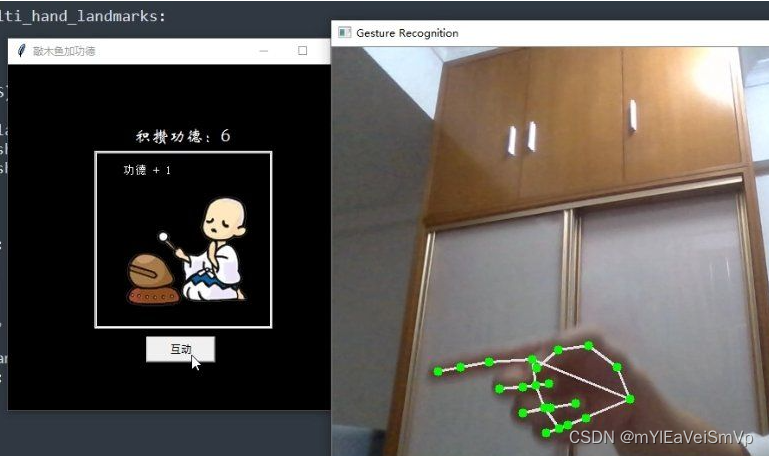
Python-敲木鱼升级版(真手动版敲木鱼)
演示效果 需要安装的第三方库: pip install pygame # 加载音乐 pip install pillow # 加载图片 pip install mediapipe # 判断手势的模型 pip install opencv # 模型要用来处理图形 建议有独显和摄像头的可以尝试! 想着升级一下玩法,只有真敲…...
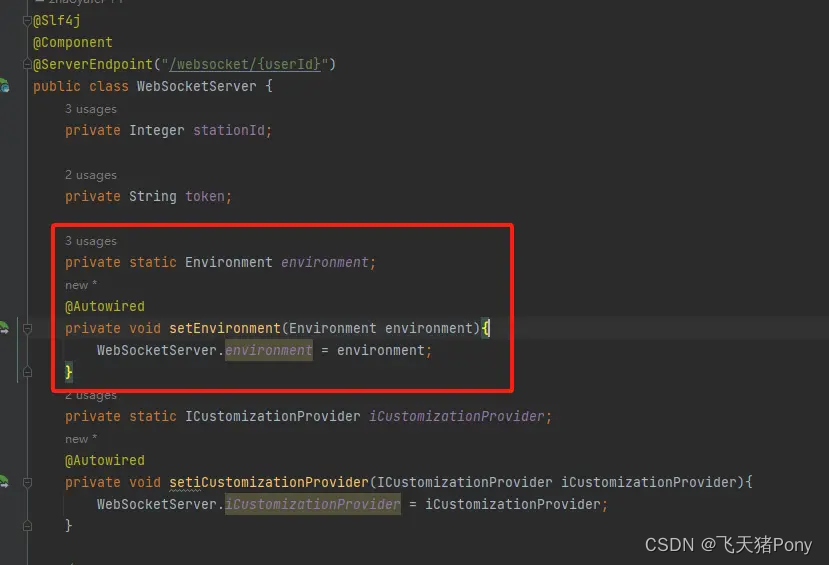
Websocket @ServerEndpoint不能注入@Autowired
在websocket中使用ServerEndpoint无法注入Autowired、Value 问题分析 Spring管理采用单例模式(singleton),而 WebSocket 是多对象的,即每个客户端对应后台的一个 WebSocket 对象,也可以理解成 new 了一个 WebSocket&…...

Unity热更新
1,热更新的概念与作用 app更新通常分为两类,一种是整包更新(换包),一种是热更新(不换包,通过网络下载,动态更新资源等)。 整包更新,是指在需要更新时&#x…...
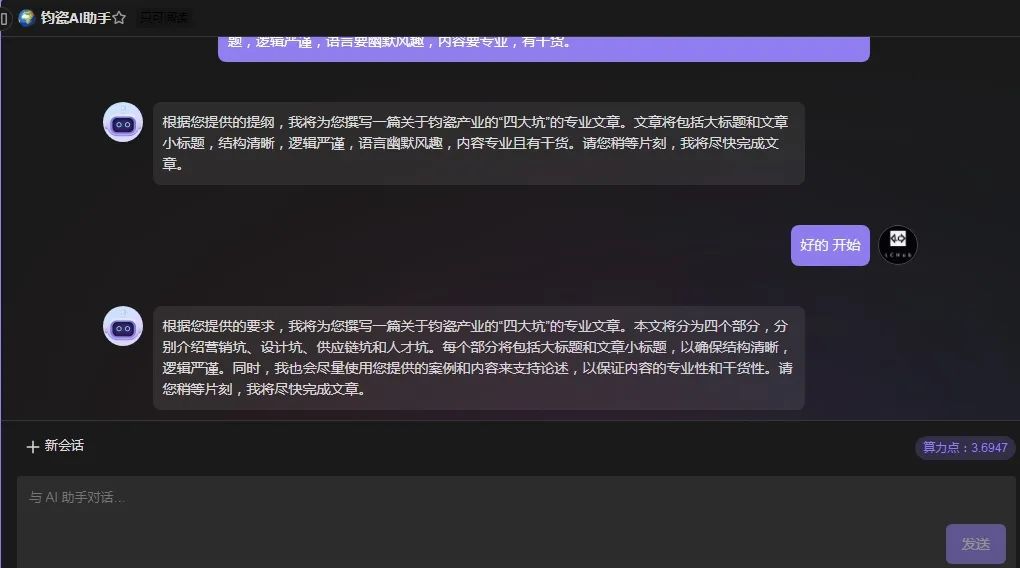
如何用维格云搭建和一键训练你的钧瓷AI机器人?
大禹智库 第69期(总第400期) 2023年11月4日 如何用维格云搭建和一键训练你的钧瓷AI机器人? 钧瓷私有数据聊天机器人是一种能够根据预设的数据集进行智能对话的机器人。通过维格云,我们可以轻松地搭建自己的钧瓷私有数据聊天机器人。本文将以钧道机器人为例,详细介绍如何…...

整理的一些Java细节问题
1. 为什么要有无参构造? 在 Java 中,如果一个类没有显式定义构造方法,编译器会自动生成一个默认的无参构造方法(也称为默认构造方法)。无参构造方法是一个没有任何参数的构造方法。 无参构造方法的存在有几个重要原因…...

初识AUTOSAR网络管理
文章目录 目的模式时间参数T_REPEAT_MESSAGET_NM_TIMEOUTT_WAIT_BUS_SLEEPT_START_Tx_AppFrameT_NM_ImmediateCycleTimeT_NM_MessageCycleN_ImmediateNM_TIMEST_START_NM_TXT_WakeUp跳转状态NM_1NM_2NM_3NM_4NM_5NM_6NM_7...

Flink SQL Hive Connector使用场景
目录 1.介绍 2.使用 2.1注册HiveCatalog 2.2Hive Read 2.2.1流读关键配置 2.2.2示例...
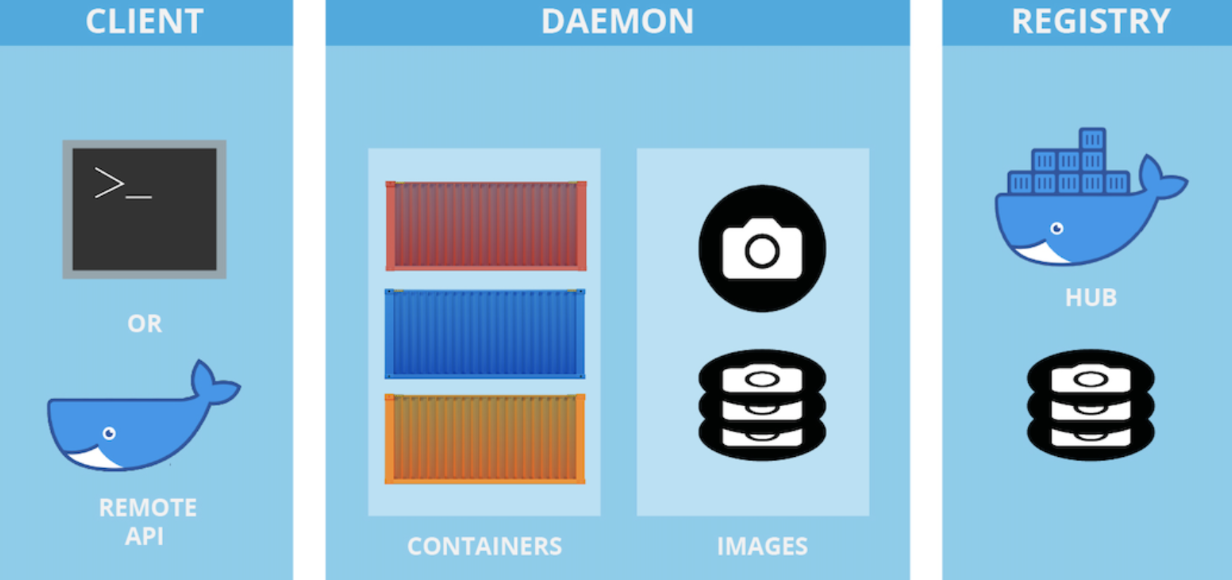
【Docker】联合探讨Docker:容器化技术的革命性应用
前言 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何接口。 📕作者简介:热…...

dirhunt使用手册,中文版
“dirhunt” 的命令行工具的帮助信息,用于目录扫描和网站内容分析。以下是这个命令的使用方法和示例: 命令格式: dirhunt [OPTIONS] [URLS]… [URLS]…:一个或多个域名或 URL,可以加载来自文件的 URL,使用…...

【从0到1设计一个网关】如何设计一个稳定的网关?
文章目录 高可用分析软件架构心跳检测自动恢复熔断降级接口重试隔离压测和预案多机房灾备以及双活数据中心异常处理机制重试主备服务自动切换动态剔除或恢复异常机器超时时间的考虑服务设计这篇文章并没有具体的业务实现,而只是对于如何设计一个高可用,稳定的网关列举出了一些…...

chromedp库编写程序
步骤1:首先,我们需要导入chromedp库,以便使用它来下载网页内容。 import chromedp 步骤2:然后,我们需要创建一个函数,该函数接受一个URL作为参数,并使用chromedp库下载该URL的内容。 func do…...

pngquant failed to build, make sure that libpng-dev is installed 问题
第一个参考方案失败 :npm install -g windows-build-tools4.0.0 安装失败,提示 依赖不在支持 第二个方案,降低node 版本 失败 第三种方案,成功 先执行,下面两行代码,再按照依赖 npm install imagemin-pn…...
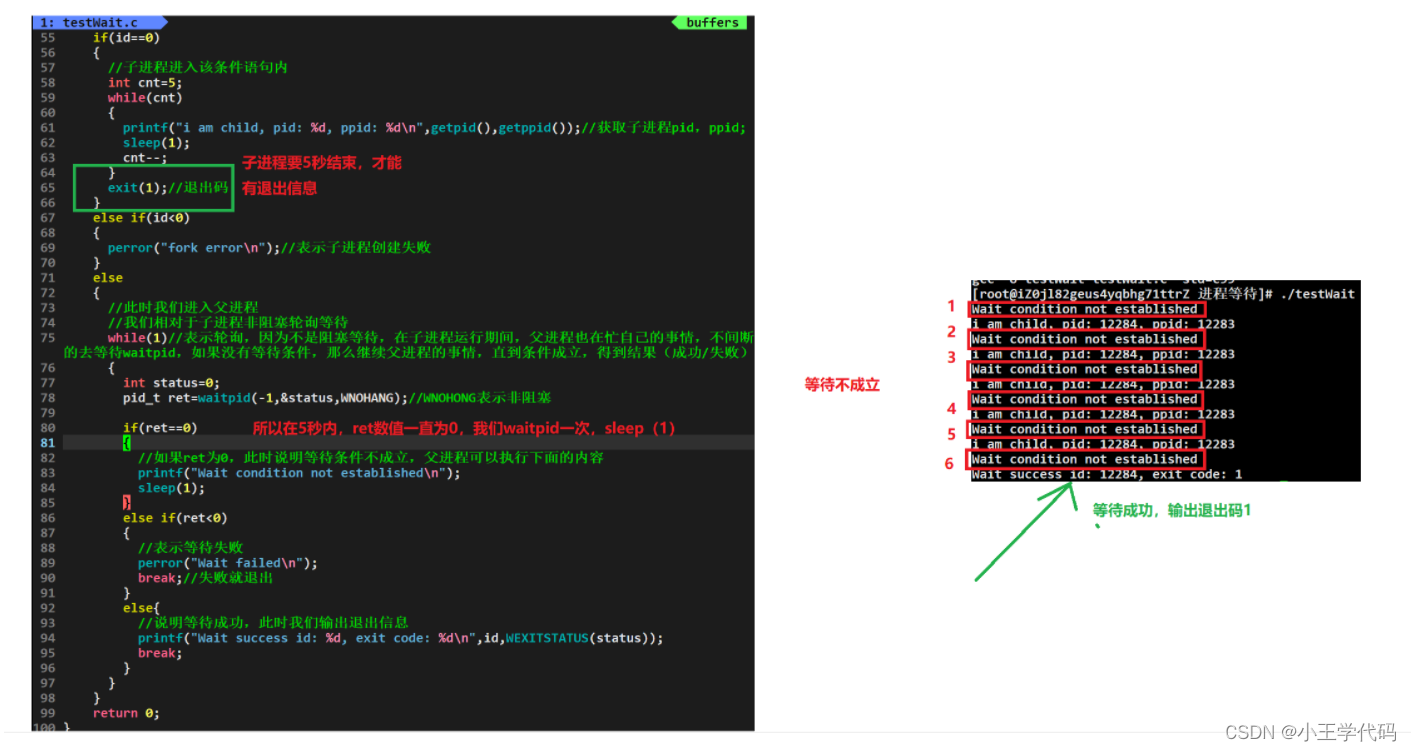
进程控制(二):进程等待
文章目录 进程控制(二)进程等待wait函数waitpid函数wait/waitpid获取子进程状态码的过程进程等待相关的宏 总结 进程控制(二) 延续对于上文进程结束,我们继续对于进程控制进行学习,本文我们主要是对于进程…...
SWAT-MODFLOW地表水与地下水耦合模型的建模及应用
目录 第一讲 模型原理与层次结构 第二讲 QGIS软件 第三讲 基于QSWATMOD的SWAT-MODFLOW模拟 第四讲 QSWAT模型介绍与建模 第五讲 基于QGIS的数据制备 第六讲 基于CUP的SWAT参数率定 第七讲 MODFLOW模型讲解 第八讲 结果分析 更多应用 耦合模型被应用到很多科学和工程领…...
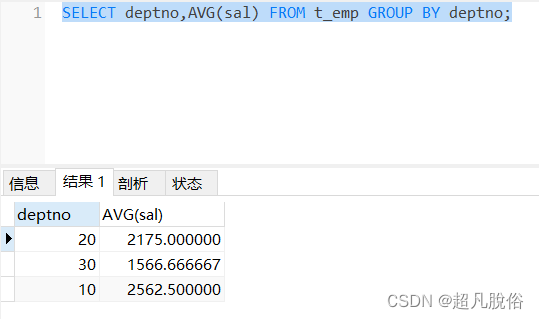
使用navicat操纵数据库
<1>连接数据库 打开Navicat,点击“连接”,选择“MySQL”,这边是本机安装的mysql,主机为localhost,输入root密码。 使用Navicat创建数据库并导入SQL文件 SQL查询 普通SQL查询 USE demo; SELECT * FROM t_emp;SELECT emp…...

websocket入门
一,什么是websocket WebSocket是HTML5下一种新的协议(websocket协议本质上是一个基于tcp的协议)它实现了浏览器与服务器全双工通信,能更好的节省服务器资源和带宽并达到实时通讯的目的Websocket是一个持久化的协议。 WebSocket有…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
