pngquant failed to build, make sure that libpng-dev is installed 问题
第一个参考方案失败 :npm install -g windows-build-tools@4.0.0
安装失败,提示 依赖不在支持
第二个方案,降低node 版本 失败
第三种方案,成功
先执行,下面两行代码,再按照依赖
npm install imagemin-pngquant --save
npm install pngquant-bin --save
第4种方案修改 host文件没有试
参考文档
https://blog.csdn.net/qq_40206575/article/details/129088419
依赖按照好后,运行时,执行npm run serve ,又报 npm install --save-dev webpack
执行
npm install --save-dev webpack
启动成功
也有这种
网上的解决办法说
是因为“这是新版webpack存在的BUG,卸载现有的新版本webpack,装老版本就好。”
1、卸载:npm uninstall webpack-dev-server
2、安装对应版本:npm install webpack-dev-server@2.9.6
相关文章:

pngquant failed to build, make sure that libpng-dev is installed 问题
第一个参考方案失败 :npm install -g windows-build-tools4.0.0 安装失败,提示 依赖不在支持 第二个方案,降低node 版本 失败 第三种方案,成功 先执行,下面两行代码,再按照依赖 npm install imagemin-pn…...
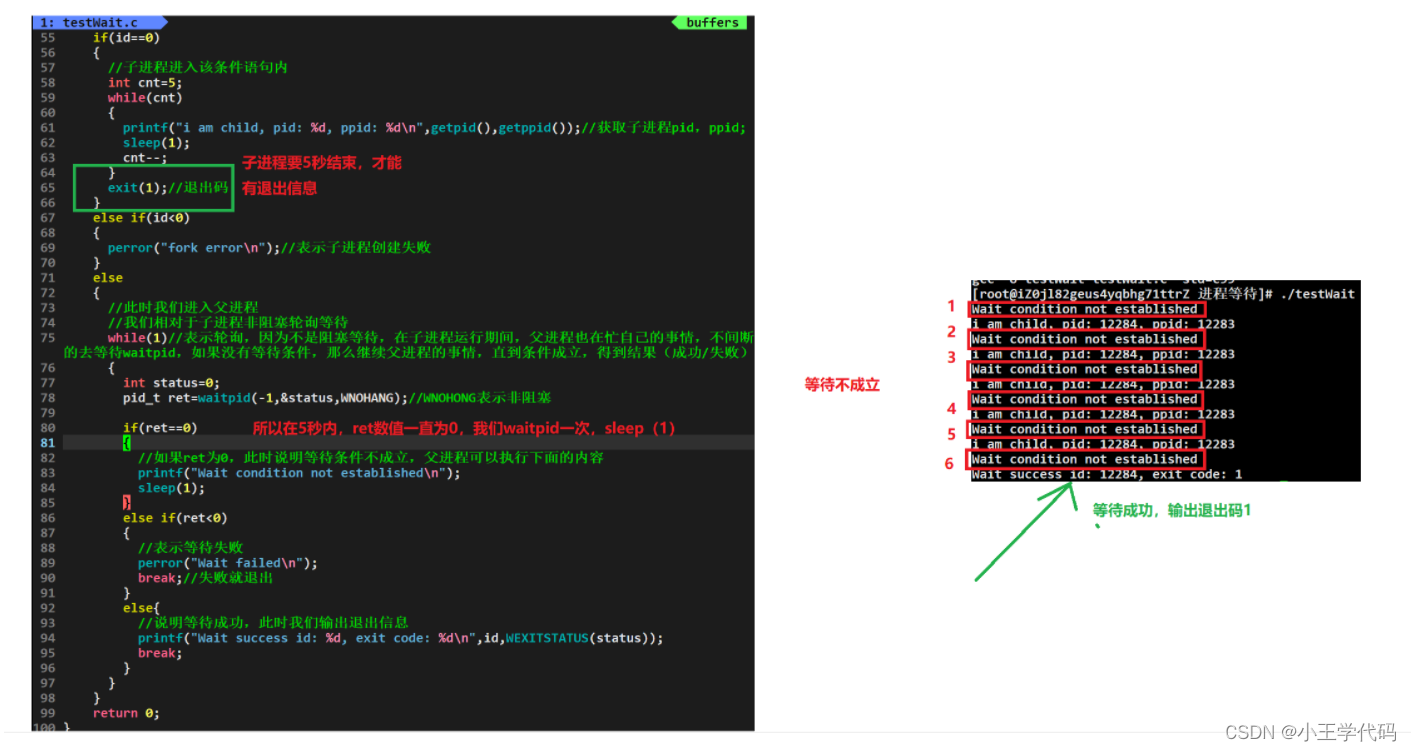
进程控制(二):进程等待
文章目录 进程控制(二)进程等待wait函数waitpid函数wait/waitpid获取子进程状态码的过程进程等待相关的宏 总结 进程控制(二) 延续对于上文进程结束,我们继续对于进程控制进行学习,本文我们主要是对于进程…...
SWAT-MODFLOW地表水与地下水耦合模型的建模及应用
目录 第一讲 模型原理与层次结构 第二讲 QGIS软件 第三讲 基于QSWATMOD的SWAT-MODFLOW模拟 第四讲 QSWAT模型介绍与建模 第五讲 基于QGIS的数据制备 第六讲 基于CUP的SWAT参数率定 第七讲 MODFLOW模型讲解 第八讲 结果分析 更多应用 耦合模型被应用到很多科学和工程领…...
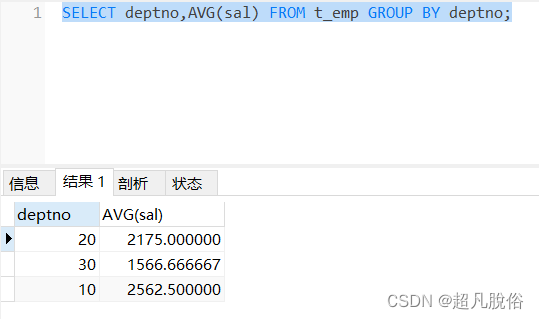
使用navicat操纵数据库
<1>连接数据库 打开Navicat,点击“连接”,选择“MySQL”,这边是本机安装的mysql,主机为localhost,输入root密码。 使用Navicat创建数据库并导入SQL文件 SQL查询 普通SQL查询 USE demo; SELECT * FROM t_emp;SELECT emp…...

websocket入门
一,什么是websocket WebSocket是HTML5下一种新的协议(websocket协议本质上是一个基于tcp的协议)它实现了浏览器与服务器全双工通信,能更好的节省服务器资源和带宽并达到实时通讯的目的Websocket是一个持久化的协议。 WebSocket有…...

Word里MathType插件符号表消失了
场景再现 在word里面编辑数学公式,结果符号表跑到屏幕外面了,找不到; 解决办法 在其中找到视图->工具栏,点击即可: 还嫌弃它跑到外边了,那就可以点击符号表的边框: 双击左边边框&#x…...

利用MySQL玩转数据分析之基础篇
知识无底,学海无涯,到今天进入MySQL的学习4天了,知识点虽然简单,但是比较多,所以写一篇博客将MySQL的基础写出来,方便自己以后查找,还有就是分享给大家。 1、SQL简述 1)SQL的概述 S…...
【ML】分类问题
分类问题 classification:根据已知样本特征,判断输入样本属于哪种已知样本类。 常用入门案例:垃圾邮件检测、图像分类、手写数字识别、考试通过预测。 分类问题和回归问题的明显区别: 分类问题的结果是非连续型标签,…...

python @classmethod装饰器作用 与 使用 类方法 实例方法
1 表示是类方法, 类方法可以修改类变量, 实例方法不能修改类变量 类方法可以访问和修改类变量(也称为类属性)。这是实例方法做不到的,因为实例方法只能访问和修改实例变量(也称为实例属性) 1.1 例子 class MyClass:…...

layui form 中input输入框长度的统一设置
Layui.form中使用class"layui-input-inline"就可轻松将元素都放到一行,但如果元素过多,就会自动换行。那就需要手动设置input框的长度。 像这种情况: 其实只需要添加css样式就可修改了 .layui-form-item .layui-input-inline {wid…...

【WSL/WSL 2-Redis】解决Windows无法安装WSL Ubuntu子系统与Redis安装
前言 在现代计算环境中,开发人员和技术爱好者通常需要在不同的操作系统之间切换,以便利用各种工具和应用程序。在这方面,Windows用户可能发现WSL(Windows Subsystem for Linux)是一个强大的工具,它允许他们…...
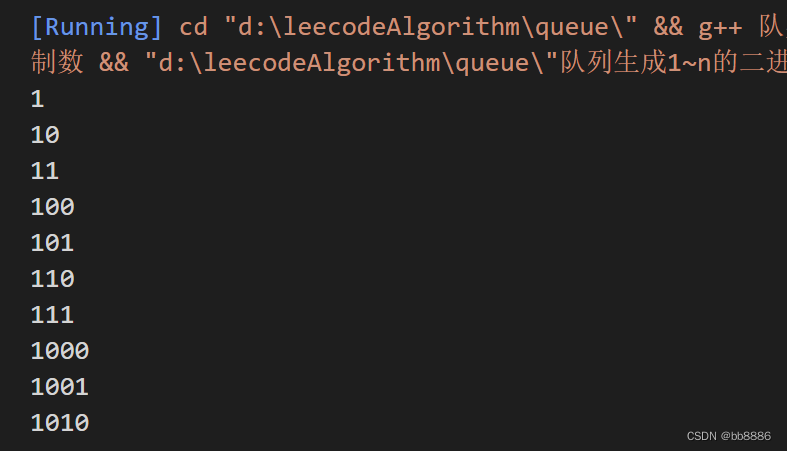
数据结构(四)--队列及面试常考的算法
一、队列介绍 1、定义 与栈相似,队列是另一种顺序存储元素的线性数据结构。栈与队列的最大差别在于栈是LIFO(后进先出),而队列是FIFO,即先进先出。 2、优缺点及使用场景 优点:先进先出(FIFO&…...
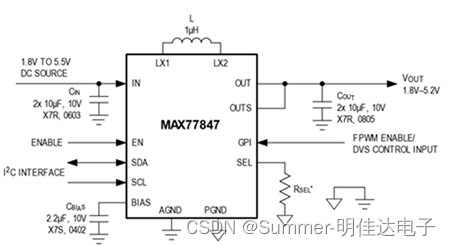
PMIC、电源管理MAX77646ANP、MAX77647AANP、MAX77675AEWE、MAX77847AEWL DC-DC 开关稳压器
一、MAX77646ANP、MAX77647AANP 低IQ SIMO PMIC支持原电池应用的1.8V工作电压 MAX77646/MAX77647为尺寸和效率至关重要的低功耗应用提供电源解决方案。该IC集成单电感多输出(SIMO)降压/升压稳压器,可通过单个电感提供三个可独立编程的电源轨,尽可能地减…...

5W2H分析法:全面思考和解决问题的实用工具
5W2H分析法又叫七问分析法,创于二战中美国陆军兵器修理部。发明者用五个以W开头的英语单词和两个以H开头的英语单词进行设问,发现解决问题的线索,寻找发明思路,进行设计构思,从而搞出新的发明项目。5W2H简单、方便&…...
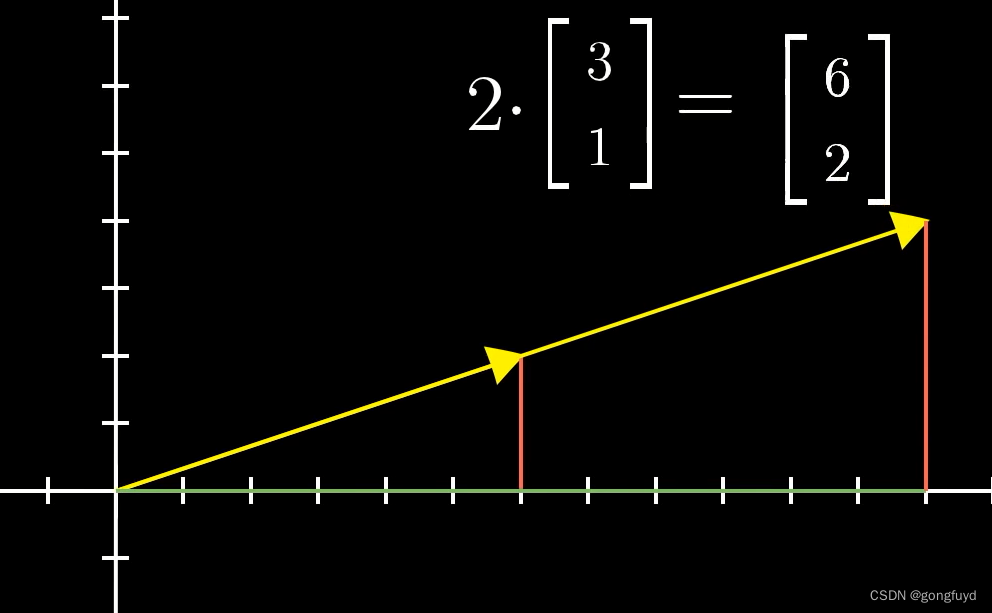
01 向量基本概念
向量基本概念 向量是什么物理专业学生视角计算机专业学生视角数学家视角 不同视角之间的关系 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 向量是什么 物理专业学生视角 向量是空间中的箭头。向量的长度和方向确定一个向量。只要长度和方向相同,…...
QMS质量检验管理|攻克制造企业质量检验难题,助力企业提质增效
在日益激烈的市场竞争中,对产品质量严格把关,是制造企业提高核心竞争力与品牌价值的关键因素。那如何高效、高质地完成产品质检工作?这就需要企业在工业质检中引进数字化技术加以辅助,进而推动智能制造高质量发展。 蓝库云QMS质量…...

Visual Components Robotics OLP解决方案 北京衡祖
Visual Components 引入了“Visual Components Robotics OLP”的重大升级,合并了制造模拟和机器人离线编程。该解决方案利用 Delfoi Robotics 的技术,提高生产率、减少停机时间并减少浪费。 一、探索下一代离线机器人编程软件 自 1999 年以来࿰…...

React——简便获取经纬度信息
引言 在现代的Web应用程序中,获取用户的地理位置信息是一项常见的需求。通过获取经纬度信息,我们可以为用户提供个性化的服务和定位功能。在本文中,我们将介绍如何在React应用程序中简便地获取用户的经纬度信息,并提供相应的代码…...
如何修改设置360浏览器内核模式
360安全浏览器现有两种内核模式,即“极速模式”和“兼容模式” 极速模式 “极速模式”是以Blink(Webkit)为内核的浏览模式,Blink内核具有更高的网页浏览速度和更好网页渲染效果。但由于少部分网银、政府、税务、办公系统等网站对B…...
不可用时并且注入失败时——笔记)
spring boot 定时任务@Scheduled(cron = ““)不可用时并且注入失败时——笔记
以下方案是本人使用定时任务时Service注入失败的解决方案 在 Spring Boot 中执行定时任务时,你可以注入并直接调用 Service 中的方法,就像在普通的业务逻辑中一样。 以下是执行定时任务时调用 Service 的步骤: 创建一个 Service 类…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
