Python算法例4 求平方根
1. 问题描述
实现int sqrt(int x)函数,计算并返回x的平方根。
2. 问题示例
sqrt(3)=1;sqrt(4)=2;sqrt(5)=2;sqrt(17)=4。
3.代码实现
要实现计算整数x的平方根函数sqrt(x),可以使用二分查找法。
首先,我们定义一个变量left = 0用来表示搜索区间的左边界,以及一个变量right = x用来表示搜索区间的右边界。初始时,我们将搜索区间设置为[0, x]。
然后,我们可以进入一个循环,直到搜索区间收敛到一个整数值。在每次循环中,我们首先计算搜索区间的中间值mid = (left + right) // 2,然后将mid的平方与x进行比较。
- 如果mid的平方等于x,那么mid就是x的平方根,直接返回mid。
- 如果mid的平方小于x,那么x的平方根应该在[mid+1, right]范围内,将left更新为mid+1。
- 如果mid的平方大于x,那么x的平方根应该在[left, mid-1]范围内,将right更新为mid-1。
当搜索区间收敛到一个整数值时,返回该整数值作为x的平方根。
def sqrt(x):if x == 0 or x == 1:return xleft, right = 0, xwhile left <= right:mid = (left + right) // 2if mid * mid == x:return midelif mid * mid < x:left = mid + 1else:right = mid - 1return rightprint(sqrt(3)) # 输出: 1
print(sqrt(4)) # 输出: 2
print(sqrt(5)) # 输出: 2
print(sqrt(17)) # 输出: 4 
class Solution:def sqrt(self,x):left = 0right = xwhile left <= right:mid = (left + right) // 2if mid * mid == x:return midelif mid * mid < x:left = mid + 1else:right = mid - 1return rightif __name__ == '__main__':temp = Solution()x1 = 5x2 = 17print(("输入:"+str(x1)))print(("输出:"+str(temp.sqrt(x1))))print(("输入:" + str(x2)))print(("输出:" + str(temp.sqrt(x2)))) 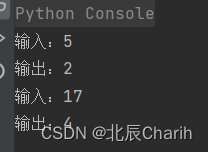
相关文章:

Python算法例4 求平方根
1. 问题描述 实现int sqrt(int x)函数,计算并返回x的平方根。 2. 问题示例 sqrt(3)1;sqrt(4)2;sqrt(5)2;sqrt(17&#…...
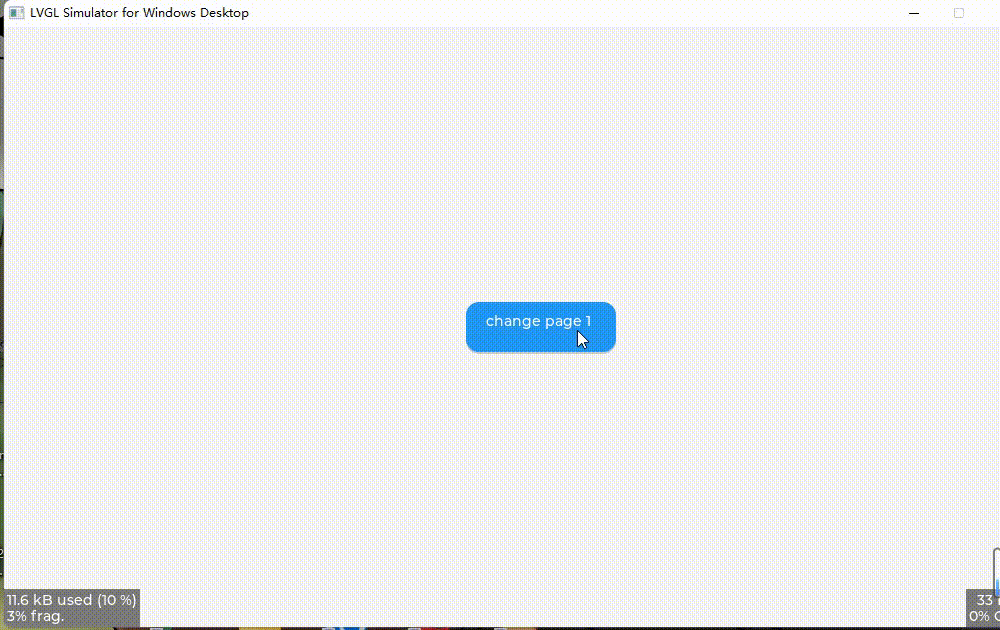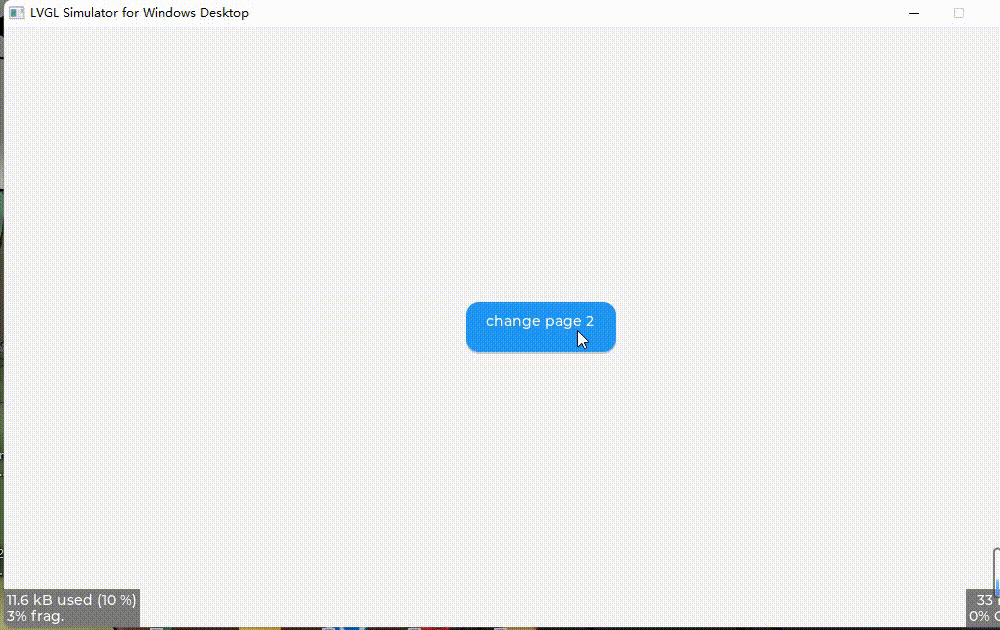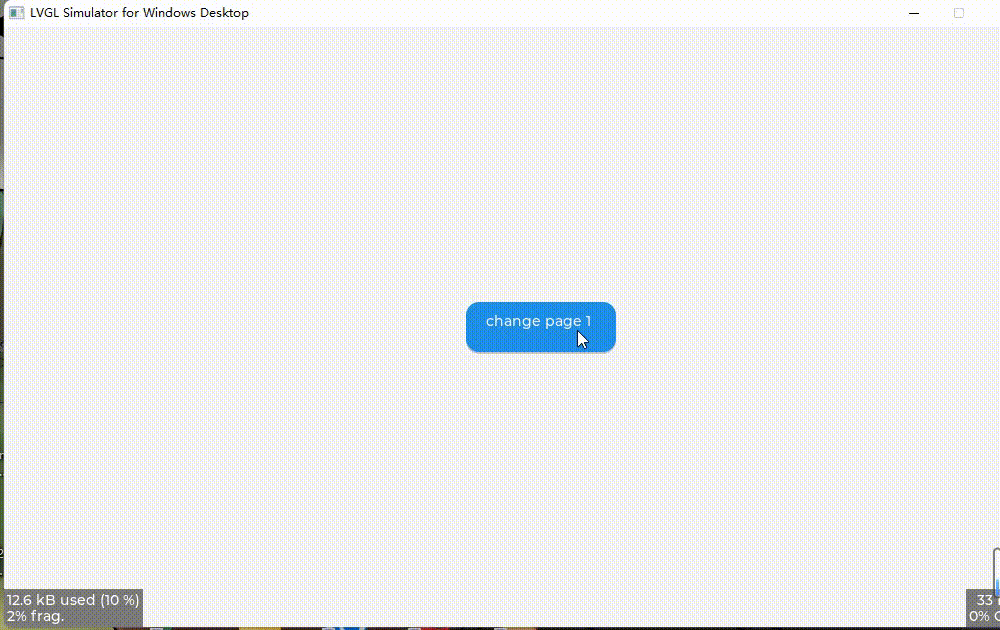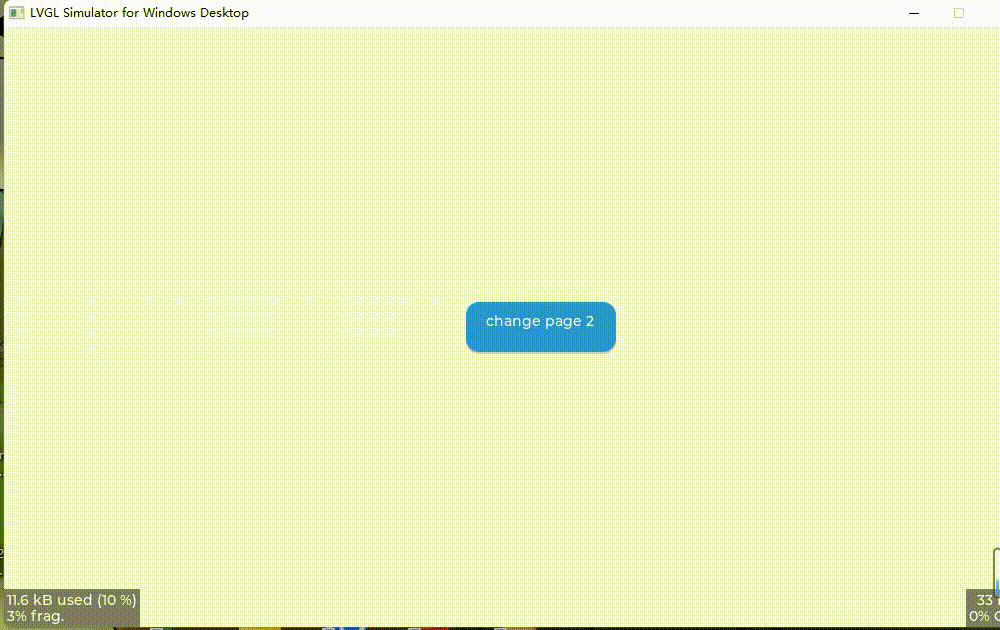
LVGL_多界面切换
LVGL_多界面切换 1、创建多个界面(create_page1();) 2、加载一个界面显示(lv_scr_load(page1);) 3、切换不同界面显示(lv_scr_load_anim(page2, LV_SCR_LOAD_ANIM_OVER_LEFT, 300, 0, false);) static lv_…...

C/C++输出字符菱形 2021年3月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C输出字符菱形 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C输出字符菱形 2021年3月 C/C编程等级考试一级编程题 一、题目要求 1、编程实现 给定一个字符,用它构造一个对角线长…...

DI93a HESG440355R3 通过其Achilles级认证提供网络安全
DI93a HESG440355R3 通过其Achilles级认证提供网络安全 施耐德电气宣布推出Modicon M580以太网PAC (ePAC)自动化控制器,该控制器采用开放式以太网标准,通过其Achilles级认证提供网络安全。M580 ePAC使工厂操作员能够设计、实施和运行一个积极利用开放网…...

Go中Panic and Recover
什么是Panic? 在 Go 程序中处理异常情况的惯用方法是使用errors.。errors足以应对程序中出现的大多数异常情况。 **但有些情况下,程序在出现异常情况后无法继续执行。在这种情况下,我们使用panic提前终止程序。当函数遇到恐慌时,…...

webpack 与 grunt、gulp 的不同?
结论先行: Webpack、Grunt 和 Gulp 都是前端开发中常用的构建工具,但是 Webpack 是基于模块化打包的工具,并支持模块化开发。而 Grunt 和 Gulp 都是基于任务的构建工具,自动执行指定的任务,但不支持模块化开发。 1、相…...

园区网真实详细配置大全案例
实现要求: 1、只允许行政部电脑对全网telnet管理 2、所有dhcp都在核心 3、wifi用户只能上外网,不能访问局域网其它电脑 4、所有接入交换机上bpdu保护 5、只允许vlan 10-40上网 5、所有接入交换机开dhcp snoop 6、所有的交换机指定核心交换机为ntp时间服务…...

小程序video标签在底部出现1px无法去除的黑色线
问题描述 参见社区问题详情 此问题只会在ios手机真机中出现,视频底部出现1px无法去除的黑色线 解决方法 1.尝试过video各种配置,以为是设置参数导致 2.尝试过父元素设置height:200px;overflow:hidden;vi…...
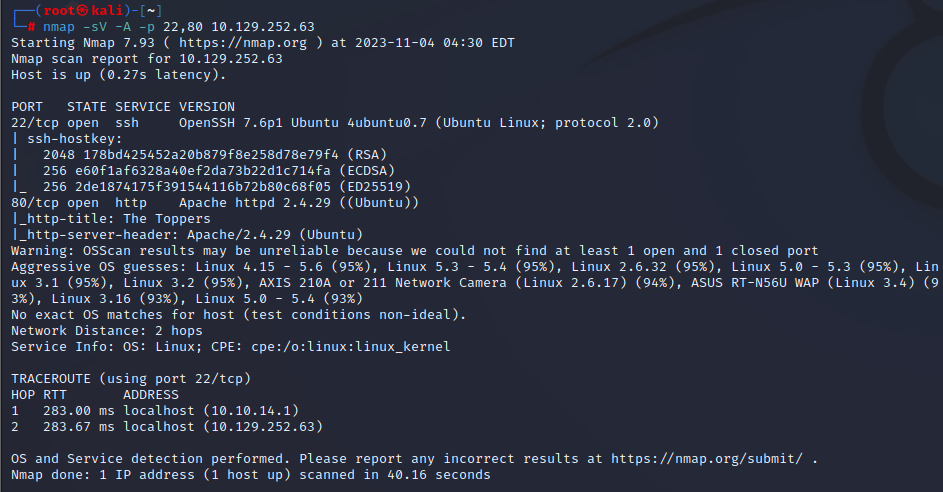
渗透工具使用及思路总结(持续更新)
扫描类 nmap 快速扫描开放端口 nmap --min-rate 10000 -p- 10.129.252.63扫描详细全服务 nmap -sV -A -p 22,80 10.129.252.63 nmap -sV -A -p- 10.129.252.63-l:显示正在监听的 TCP 和 UDP 端口; -a:显示所有活动的 TCP 连接; -A <网络类型>或 - <网络类型&g…...

速卖通新卖家有必要测评吗?
大家都知道通过测评可以提升产品的转化率,提升产品的销量,那么做速卖通的卖家有必要测评吗? 测评就是类似于国内电商的补单,而一个类目里面竞争很大很卷的话,不去补销量来提升产品的权重,凭借着平台给的自…...
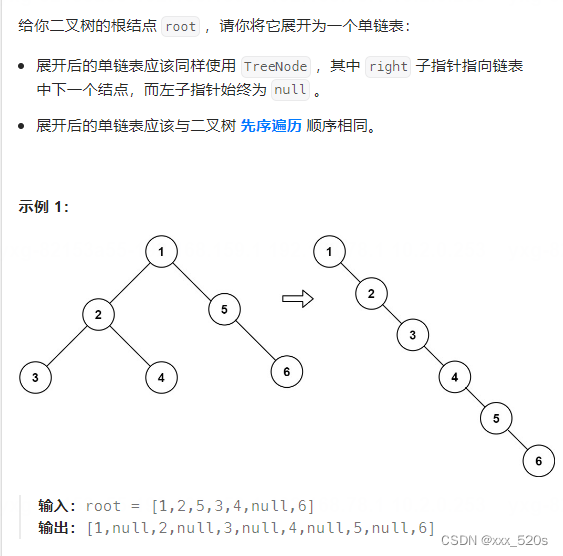
从lc114. 二叉树展开为链表到lc-LCR 155二叉搜索树转化为排序的双向链表
1 lc114. 二叉树展开为链表 1.1 描述 进阶:你可以使用原地算法(O(1) 额外空间)展开这棵树吗? 1.2 解法一: 先序遍历这棵树并且将节点加入到一个list中,随后按顺序将list中的每一个元素的left指针置换为…...
做读书笔记时的一个高效小技巧
你好,我是 EarlGrey,一名双语学习者,会一点编程,目前已翻译出版《Python 无师自通》、《Python 并行编程手册》等书籍。 在这里,我会持续和大家分享好书、好工具和高效生活、工作技巧,欢迎大家一起提升认知…...
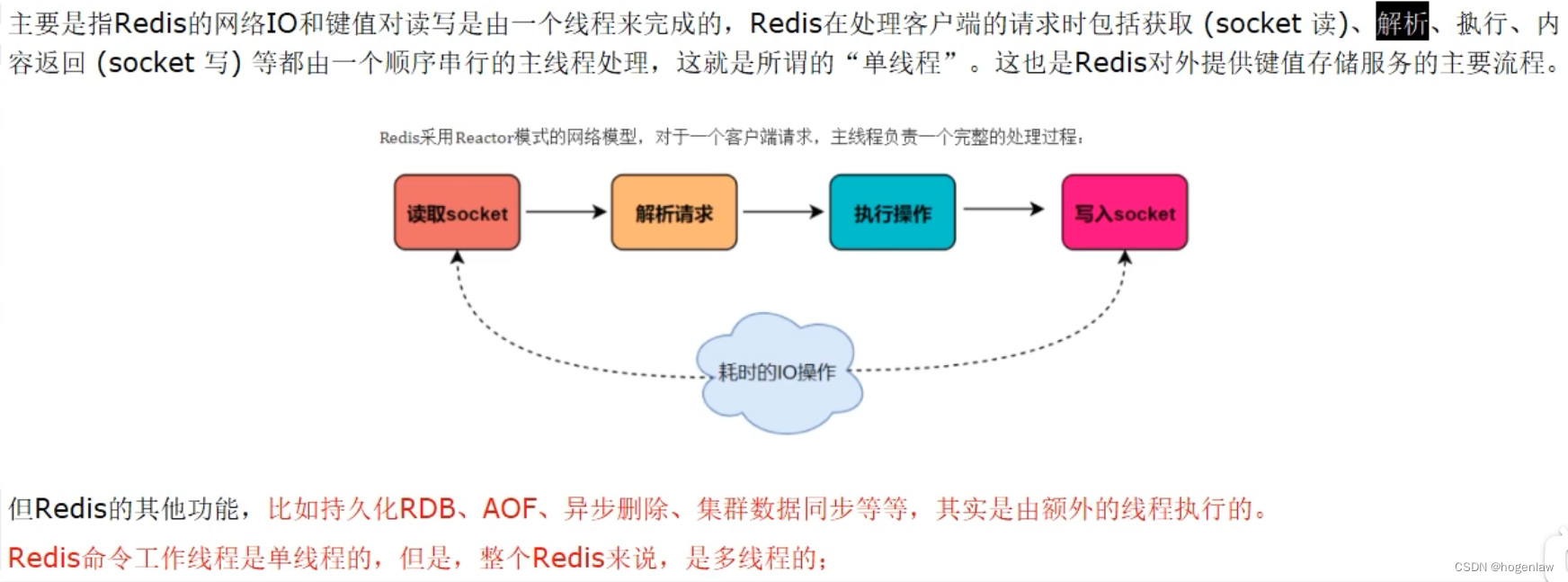
Redis7.x 高级篇
Redis7.x 高级篇 Redis版本发行时间Redis单线程说的是什么东西 Redis版本发行时间 Redis单线程说的是什么东西...

2023辽宁省数学建模B题数据驱动的水下导航适配区分类预测完整原创论文分享(python求解)
大家好呀,从发布赛题一直到现在,总算完成了辽宁省数学建模B题完整的成品论文。 本论文可以保证原创,保证高质量。绝不是随便引用一大堆模型和代码复制粘贴进来完全没有应用糊弄人的垃圾半成品论文。 B用Python+SPSSPRO求解&…...

向量数据库的崛起与多元化场景创新
向量数据库的崛起与多元化场景创新 前言: 在当今数字化时代,数据被认为是黄金,对于企业、科学家和决策者而言都具有巨大的价值。然而,随着数据规模的不断增长,有效地管理、存储和检索数据变得愈发复杂。这就引入了向量…...
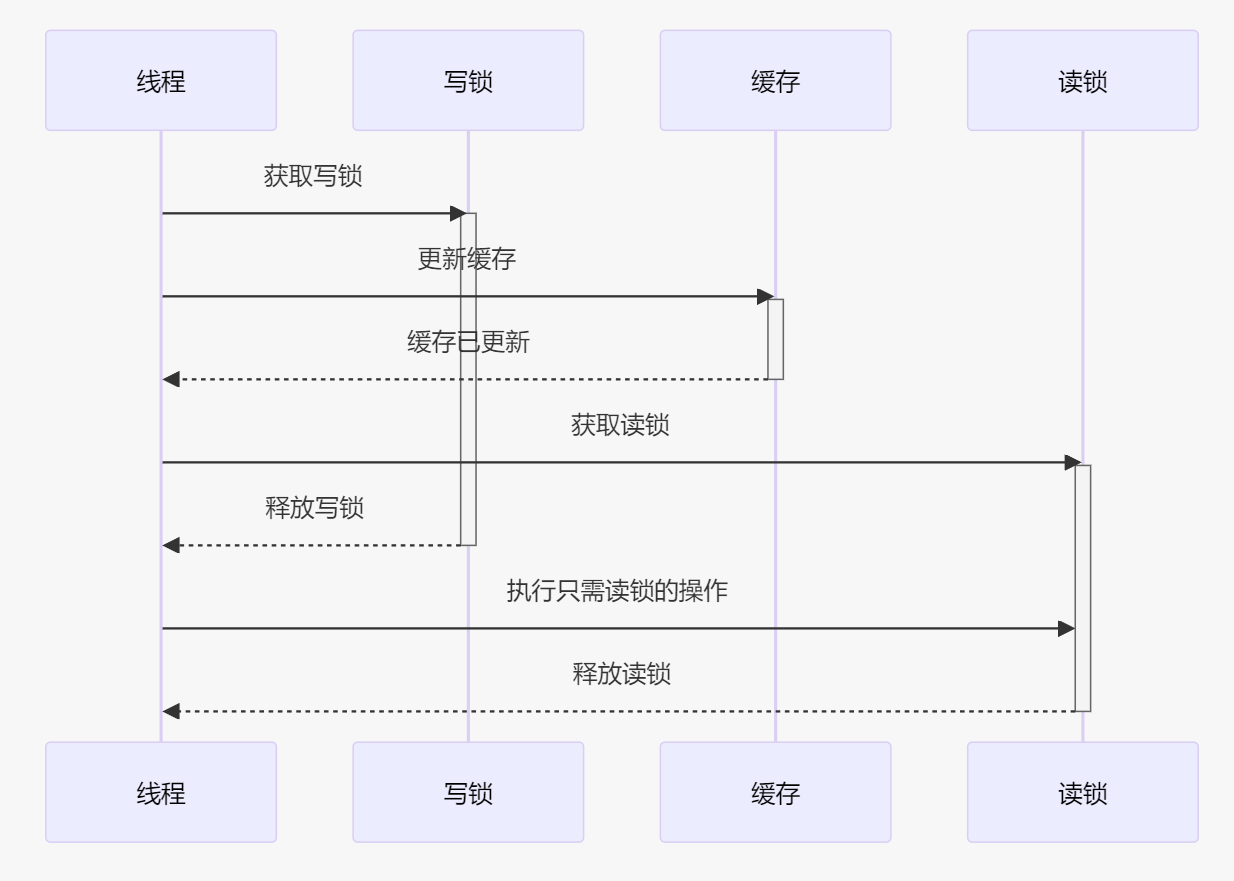
面试10000次依然会问的【ReentrantLock】,你还不会?
引言 在并发编程的世界中,ReentrantLock扮演着至关重要的角色。它是一个实现了重入特性的互斥锁,提供了比synchronized关键字更加灵活的锁定机制。ReentrantLock属于java.util.concurrent.locks包,是Java并发API的一部分。 与传统的synchro…...
Bat批量处理
一:创建文件夹 excel创建文件 复制出来新建文本文件 另存为bat 双击bat 二:批量移动文件 A列:获取的文件名列表 dir /b/o:n> original.txt B列:填充序号 C列公式:每隔9行增加1 INT((ROW(B1)-1)/9)1 D列公式&am…...
【一、http】go的http基本请求方法
1、http的基本请求 package mainimport ("bytes""fmt""io""net/http""net/url" )func post(){r, err : http.Post("http://httpbin.org/post", "", nil)if err ! nil {fmt.Println("ss")}de…...

【软考中级】软件设计师-下午题
下午题 试题一 黑洞:加工有输入无输出 白洞(奇迹):加工有输出无输入 灰洞:数据流输入的加工不足以产生输出 结构化语言: IF *** THEN ELSE IF *** THEN ******* END IF END IF 数据流的父子图平衡,如果父子图平衡就不…...
Mycat实现读写分离)
(03)Mycat实现读写分离
1、schema.xml <?xml version"1.0"?> <!DOCTYPE mycat:schema SYSTEM "schema.dtd"> <mycat:schema xmlns:mycat"http://io.mycat/"><schema name"TESTDB" checkSQLschema"false" sqlMaxLimit"…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
