PTA: 矩阵的乘法运算
矩阵的乘法运算
- 题目
- 输入格式
- 输出格式
- 输入样例
- 输出样例
- 代码
题目
线性代数中的矩阵可以表示为一个row*column的二维数组,当row和column均为1时,退化为一个数,当row为1时,为一个行向量,当column为1时,为一个列向量。
建立一个整数矩阵类matrix,其私有数据成员如下:
int row;
int column;
int **mat;
建立该整数矩阵类matrix构造函数;
建立一个 *(乘号)的运算符重载,以便于对两个输入矩阵进行乘法运算;
建立输出函数void display(),对整数矩阵按行进行列对齐输出,格式化输出语句如下:
cout<<setw(10)<<mat[i][j];
//需要#include <iomanip>
主函数里定义三个整数矩阵类对象m1、m2、m3.
、
输入格式
分别输入两个矩阵,分别为整数矩阵类对象m1和m2。
每个矩阵输入如下:
第一行两个整数 r c,分别给出矩阵的行数和列数
接下来输入r行,对应整数矩阵的每一行
每行输入c个整数,对应当前行的c个列元素
输出格式
整数矩阵按行进行列对齐(宽度为10)后输出
判断m1和m2是否可以执行矩阵相乘运算。
若可以,执行m3=m1*m2运算之后,调用display函数,对m3进行输出。
若不可以,输出"Invalid Matrix multiplication!"
提示:输入或输出的整数矩阵,保证满足row>=1和column>=1。
输入样例
4 5
1 0 0 0 5
0 2 0 0 0
0 0 3 0 0
0 0 0 4 0
5 5
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 8 9
5 6 7 8 9
输出样例
26 32 38 44 504 6 8 10 129 12 15 18 2116 20 24 32 36
代码
#include <iostream>
#include <iomanip>
using namespace std;
class matrix{
private:int row,column;int **mat;
public:matrix(const matrix& mx){this->row=mx.row;this->column=mx.column;this->mat=new int*[row];for (int i = 0; i <row ; ++i) {this->mat[i]=new int[column];for (int j = 0; j <column ; ++j) {this->mat[i][j]=mx.mat[i][j];}}}matrix(int r,int c){row=r;column=c;mat=new int*[row];for (int i = 0; i <row ; ++i) {mat[i]=new int[column];for (int j = 0; j <column ; ++j) {mat[i][j]=0;}}}~matrix(){for (int i = 0; i <row ; ++i) {delete []mat[i];}delete []mat;}void read(){for (int j = 0; j <row ; ++j) {for (int i = 0; i <column ; ++i) {cin>>mat[j][i];}}}matrix operator*(matrix& mt){if(this->row==1&&this->column==1){for (int i = 0; i < mt.row; ++i) {for (int j = 0; j <mt.column ; ++j) {mt.mat[i][j]=this->mat[0][0]*mt.mat[i][j];}}return mt;}else{matrix rs(this->row,mt.column);for (int i = 0; i < this->row; ++i) {for (int j = 0; j <mt.column ; ++j) {for (int k = 0; k <mt.row ; ++k) {rs.mat[i][j]+=this->mat[i][k]*mt.mat[k][j];}}}return rs;}}void display(){for (int i = 0; i <row ; ++i) {for (int j = 0; j <column ; ++j) {cout<<setw(10)<<mat[i][j];}cout<<endl;}}
};
int main()
{int r,c;cin>>r>>c;matrix m1(r,c);m1.read();int r1,c1;cin>>r1>>c1;matrix m2(r1,c1);m2.read();if(c==r1||r==1&&c==1){matrix m3=m1*m2;m3.display();}else{cout<<"Invalid Matrix multiplication!";}return 0;
}
相关文章:

PTA: 矩阵的乘法运算
矩阵的乘法运算 题目输入格式输出格式输入样例输出样例 代码 题目 线性代数中的矩阵可以表示为一个row*column的二维数组,当row和column均为1时,退化为一个数,当row为1时,为一个行向量,当column为1时&…...
4K Video Downloader Pro v4.28.0(视频下载器)
4K Video Downloader Pro是一款专业的视频下载软件,支持从YouTube、Vimeo、Facebook、Instagram、TikTok等主流视频网站下载高质量的4K、HD和普通视频。它的操作流程简单,只需复制视频链接并粘贴到软件中即可开始下载。此外,该软件还提供了多…...

java pdf,word,ppt转图片
pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0…...
map set
目录 一、关联式容器 二、键值对 三、树形结构的关联式容器 3.1 set 3.1.1 set的介绍 3.1.2 set的使用 3.2 multiset 3.2.1 multiset的介绍 3.2.2 multiset的使用 3.3 map 3.3.1 map的介绍 3.3.2 map的使用 …...
Fourier分析导论——第3章——Fourier级数的收敛性(E.M. Stein R. Shakarchi)
第 3 章 Fourier级数的收敛性(Convergence of Fourier Series) The sine and cosine series, by which one can represent an arbitrary function in a given interval, enjoy among other remarkable properties that of being convergent. This property did not escape…...
解决ruoyi-vue部署到域名子路径静态资源404
参考ruoyi前端手册...

游戏引擎中为什么要用四元数表示旋转而不用欧拉角旋转?
个人观点,仅供参考,如有错误可太刺激了 四元数的简单概念和使用 欧拉角通常用于表示一个物体的旋转状态,而不是表示旋转过程。 欧拉角描述的是物体相对于某个参考坐标系的朝向或旋转状态,通常以不同的轴(例如&#x…...
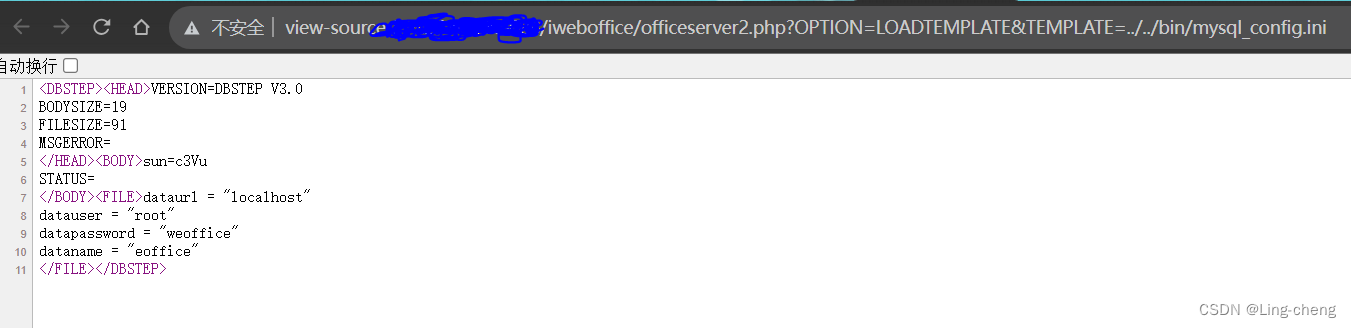
E-Office(泛微OA)前台任意文件读取漏洞复现
简介 泛微E-Office是一款企业级的全流程办公自动化软件,它包括协同办公、文档管理、知识管理、工作流管理等多个模块,涵盖了企业日常工作中的各个环节。在该产品前台登录页存在文件读取漏洞。 officeserver.php文件存在任意文件读取漏洞,通…...

前端小案例 | 喵喵大王立大功 | 一个带便利贴功能的todolist面板
文章目录 📚html📚css📚js🐇stickynote.js🐇todolist.js🐇clock.js 📚html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><m…...

算法训练营第十一天 | 20. 有效的括号、 1047. 删除字符串中的所有相邻重复项、150. 逆波兰表达式求值
目录: 力扣 20. 有效的括号力扣 1047. 删除字符串中的所有相邻重复项力扣 150. 逆波兰表达式求值 问题一、 20. 有效的括号 题目链接:20. 有效的括号 - 力扣(LeetCode) 思路分析: 很多朋友刚开始接触这一类题的时候…...
Python unittest单元测试框架 TestSuite测试套件
TestSuite 测试套件简介 对一个功能的验证往往是需要很多多测试用例,可以把测试用例集合在一起执行,这就产生了测试套件TestSuite 的概念,它是用来组装单个测试用例,规定用例的执行的顺序,而且TestSuite也可以嵌套Tes…...

FSB逮捕为乌克兰网络部队工作的俄罗斯黑客
导语 近日,俄罗斯联邦安全局(FSB)逮捕了两名涉嫌协助乌克兰网络部队对俄罗斯重要基础设施目标进行网络攻击的个人。这起事件引起了广泛关注,涉及到了网络安全和国际关系等多个领域。本文将为您详细介绍这一事件的背景和最新进展。…...
【PC电脑windows-学习样例tusb_serial_device-ESP32的USB模拟串口程序+VScode建立工程+usb组件添加+-基础样例学习】
【PC电脑windows-学习样例tusb_serial_device-ESP32的USB模拟串口程序-基础样例学习】 1、概述2、实验环境3-1、 物品说明3-2、所遇问题:ESP32 cannot open source file "tinyusb.h"或者“tinyusb.h:No such file or directory ....”3-3、解决问题&#…...

LeetCode75——Day26
文章目录 一、题目二、题解 一、题目 394. Decode String Given an encoded string, return its decoded string. The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guar…...
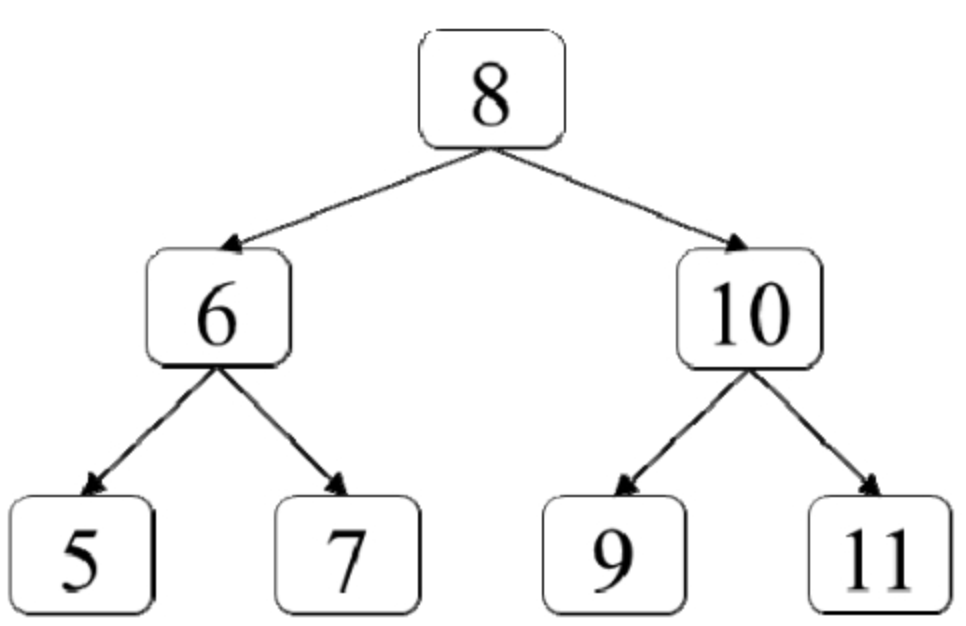
面试算法53:二叉搜索树的下一个节点
题目 给定一棵二叉搜索树和它的一个节点p,请找出按中序遍历的顺序该节点p的下一个节点。假设二叉搜索树中节点的值都是唯一的。例如,在图8.9的二叉搜索树中,节点8的下一个节点是节点9,节点11的下一个节点是null。 分析…...

2023SHCTF web方向wp
1.ezphp 看一眼,你大爷,啥玩意都给我过滤完了。 还好下面有preg_replace()/e,会把replacement当作php语句执行 传参pattern.*, .*表示任意字符,code{${phpinfo()}} ,为什么这样写,因为,print_…...
从物理磁盘到数据库 —— 存储IO链路访问图
原图来自:数据库IO链路访问图 – OracleBlog 由于很复杂,为了加深理解自己重新画了一次,另外参考其他文档补充了各部分的插图和介绍。 一、 存储服务器 1. 物理磁盘 外层的壳子称为硬盘笼 cage 2. chunklet Chunklet 是一个虚拟概念而不是实…...
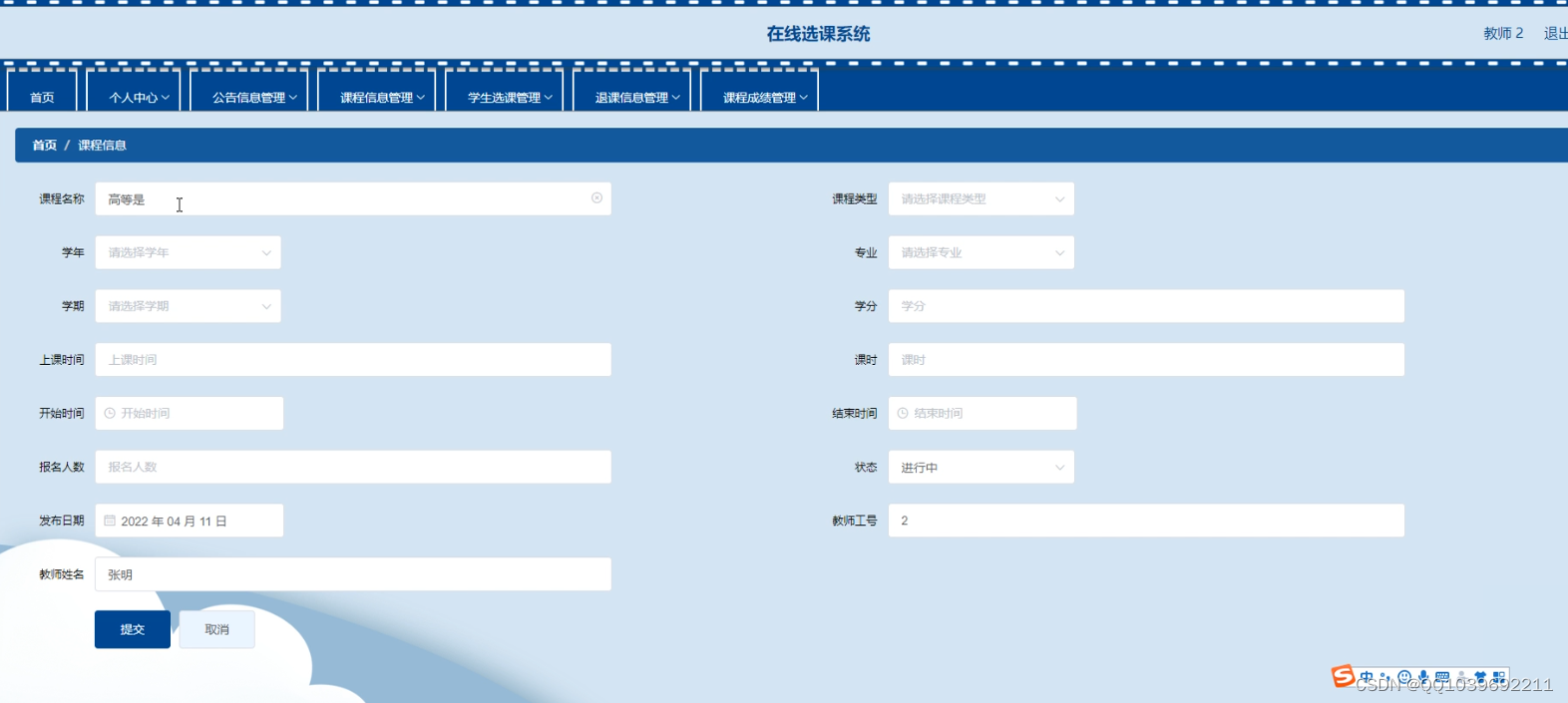
基于java+springboot+vue在线选课系统
项目介绍 本系统结合计算机系统的结构、概念、模型、原理、方法,在计算机各种优势的情况下,采用JAVA语言,结合SpringBoot框架与Vue框架以及MYSQL数据库设计并实现的。员工管理系统主要包括个人中心、课程管理、专业管理、院系信息管理、学生…...

GO学习之 同步操作sync包
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 10、GO学习之 网络通信(Net/Htt…...
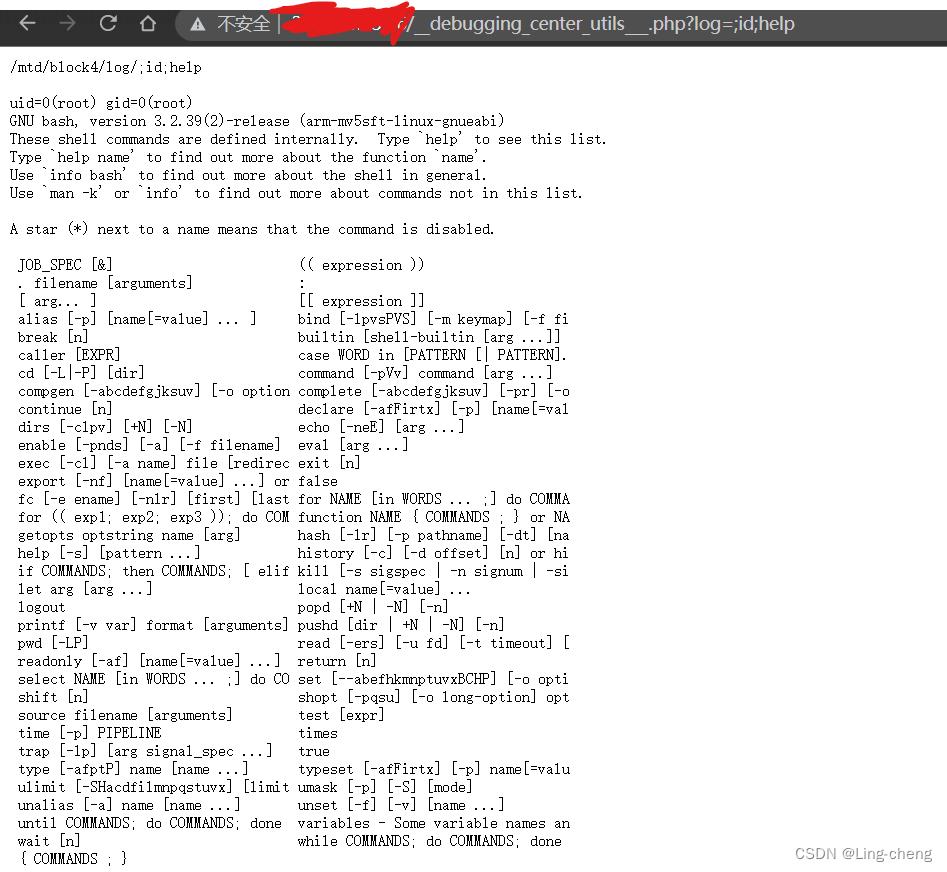
NUUO网络摄像头(NVR)RCE漏洞复现
简介 NUUO Network Video Recorder(NVR)是中国台湾NUUO公司的一款网络视频记录器。 NUUO NVR视频存储管理设备的__debugging_center_utils___.php文件存在未授权远程命令执行漏洞,攻击者可在没有任何权限的情况下通过log参数执行任意命令。…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

Qt Quick Dialogs模块功能及架构
Qt Quick Dialogs 是 Qt Quick 的一个附加模块,提供了一套用于创建和使用系统对话框的 QML 类型。在 Qt 6.0 中,这个模块经过了重构和增强。 一、主要功能和特点 1. 对话框类型 Qt Quick Dialogs 在 Qt 6.0 中提供了以下标准对话框类型: …...

我认为STM32输入只分为模拟输入 与 数字输入
核心概念解析 模拟输入 (Analog Input) 设计目的:直接连接模拟信号(如ADC采集电压、温度传感器输出) 硬件行为: ✅ 断开内部数字电路(施密特触发器禁用) ✅ 信号直通模拟外设(如ADC、运放&…...

uni-app 项目支持 vue 3.0 详解及版本升级方案?
uni-app 支持 Vue 3.0 详解及升级方案 一、uni-app 对 Vue 3.0 的支持现状 uni-app 从 3.0 版本 开始支持 Vue 3.0,主要变化包括: 核心框架升级: 基于 Vue 3.0 的 Composition API 和 Options API 双模式支持提供 vueuse/core 等组合式 API…...

自然语言处理——语言模型
语言模型 n元文法参数估计数据平滑方法加1法 神经网络模型提出原因前馈神经网络(FNN)循环神经网络 n元文法 大规模语料库的出现为自然语言统计处理方法的实现提供了可能,统计方法的成功应用推动了语料库语言学的发展。 语句 𝑠 …...
