IDEA 设置代码注释模板
功能简介:
每次看别人代码时,面对毫无注释的类,除了头大还是头大,
以下提供了一种代码类注释模板
新建java类的时候,自动增加类注释,养成代码开发好习惯
效果展示:
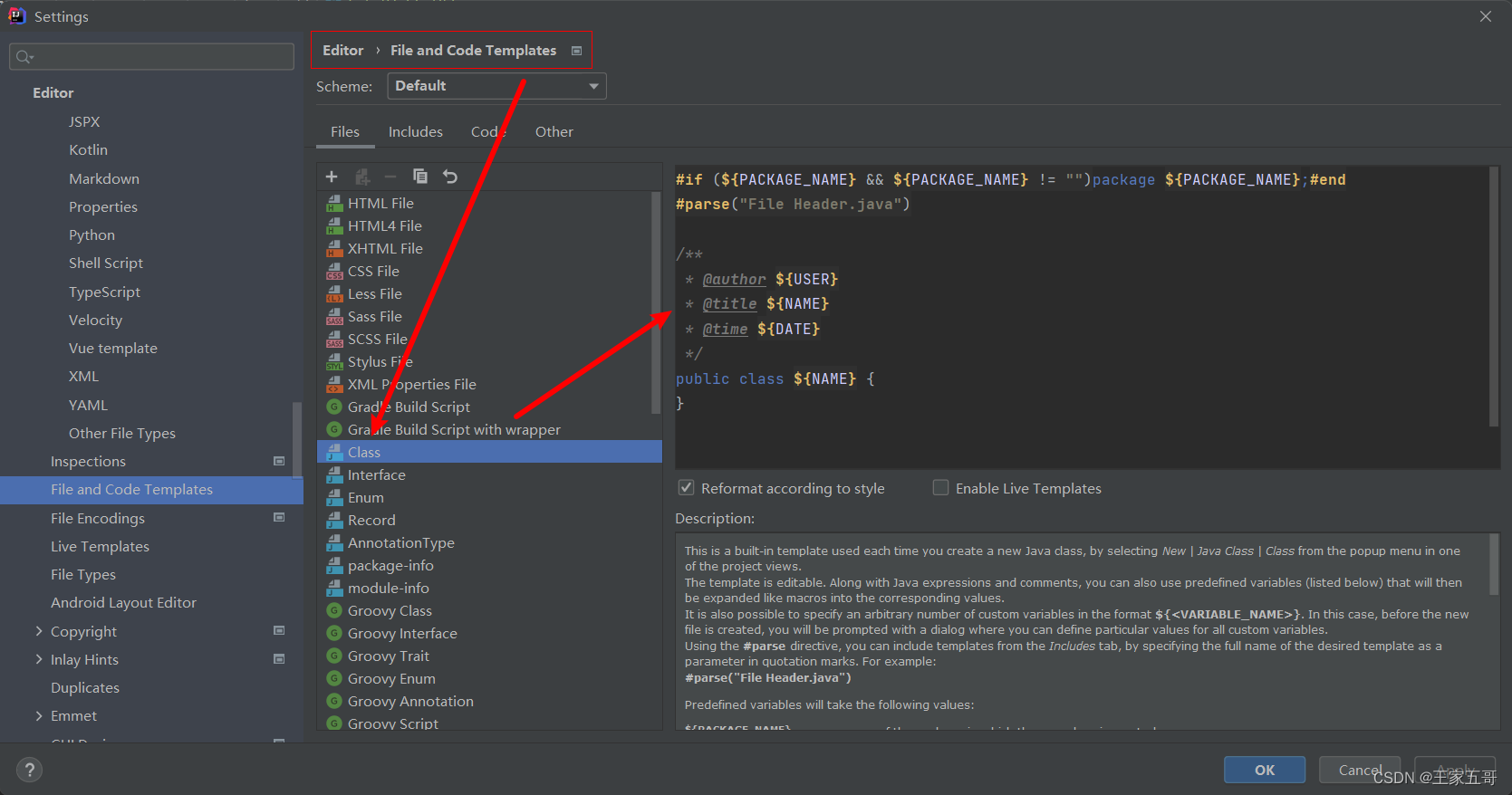
代码模板:
#if (${PACKAGE_NAME} && ${PACKAGE_NAME} != "")package ${PACKAGE_NAME};#end
#parse("File Header.java")/*** @author ${USER}* @title TODO* @time ${DATE}*/
public class ${NAME} {
}
/*** ${DESCRIPTION}** This is a ${PURPOSE} that provides ${FUNCTIONALITY}.* It is designed to ${INTENDED_USE_CASE}.** @author ${AUTHOR}* @since ${DATE}* @version ${VERSION}*/
在上述注释模板中,您可以根据需要替换以下占位符:
${DESCRIPTION}:简单描述类或方法的目的和功能。${PURPOSE}:说明代码的目的或用途。${FUNCTIONALITY}:指出代码提供的具体功能。${INTENDED_USE_CASE}:描述代码的预期使用场景。
此外,还有一些固定的占位符,无需手动替换:
${AUTHOR}:自动生成为当前用户。${DATE}:自动生成为当前日期。${VERSION}:指定代码版本号(可以手动填写)。
设置代码注释模板的步骤如下:
- 打开 IntelliJ IDEA。
- 进入 "Preferences"(macOS)或 "Settings"(Windows/Linux)。
- 在设置窗口中,选择 "Editor" -> "File and Code Templates"。
- 在右侧的模板列表中,选择 "Includes" -> "File Header"。
- 在编辑器中,将上述代码注释模板复制并粘贴到现有模板中。
- 根据您的需求,修改注释模板并保存设置。
这样,当您在 IntelliJ IDEA 中创建新的类或方法时,注释将根据模板自动生成,并在生成注释时替换相应的占位符。
相关文章:

IDEA 设置代码注释模板
功能简介: 每次看别人代码时,面对毫无注释的类,除了头大还是头大, 以下提供了一种代码类注释模板 新建java类的时候,自动增加类注释,养成代码开发好习惯 效果展示: 代码模板: #if (…...

emoji对齐 特殊字符对齐 文本对齐
emoji如何对齐 特殊字符如何对齐 高级文本对齐 问题引出 我们在程序打印输出时,如何我们所输出的字符中包含emoji文本,或者其它特殊的字符文本,则我们的打印对齐效果将出现错位。以下代码复现了这一效果(tips: 马老师…...

Selenium Python 中的动作链
Selenium 是一个用于自动化的独立的基于 Web 的工具。 它是任何人都可以使用的开源工具。 与Python语言结合使用该工具进行测试。 操作链是 Selenium 的基本组成部分,提供了一种管理低级交互的方法,例如按键、鼠标移动、鼠标按钮操作以及与上下文菜单的…...
OceanBase:03-集群部署
目录 一、集群规划 二、配置要求 三、部署前配置 1.配置 limits.conf 2.配置 sysctl.conf 3.关闭防火墙 4.关闭 SELinux 5.创建数据目录,修改文件所有者信息 6.设置无密码 SSH 登录 7.安装jdk 四、解压执行安装 五、集群部署 1.OBD命令行部署 2. OBD白…...

PTA: 矩阵的乘法运算
矩阵的乘法运算 题目输入格式输出格式输入样例输出样例 代码 题目 线性代数中的矩阵可以表示为一个row*column的二维数组,当row和column均为1时,退化为一个数,当row为1时,为一个行向量,当column为1时&…...
4K Video Downloader Pro v4.28.0(视频下载器)
4K Video Downloader Pro是一款专业的视频下载软件,支持从YouTube、Vimeo、Facebook、Instagram、TikTok等主流视频网站下载高质量的4K、HD和普通视频。它的操作流程简单,只需复制视频链接并粘贴到软件中即可开始下载。此外,该软件还提供了多…...

java pdf,word,ppt转图片
pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0…...
map set
目录 一、关联式容器 二、键值对 三、树形结构的关联式容器 3.1 set 3.1.1 set的介绍 3.1.2 set的使用 3.2 multiset 3.2.1 multiset的介绍 3.2.2 multiset的使用 3.3 map 3.3.1 map的介绍 3.3.2 map的使用 …...
Fourier分析导论——第3章——Fourier级数的收敛性(E.M. Stein R. Shakarchi)
第 3 章 Fourier级数的收敛性(Convergence of Fourier Series) The sine and cosine series, by which one can represent an arbitrary function in a given interval, enjoy among other remarkable properties that of being convergent. This property did not escape…...
解决ruoyi-vue部署到域名子路径静态资源404
参考ruoyi前端手册...

游戏引擎中为什么要用四元数表示旋转而不用欧拉角旋转?
个人观点,仅供参考,如有错误可太刺激了 四元数的简单概念和使用 欧拉角通常用于表示一个物体的旋转状态,而不是表示旋转过程。 欧拉角描述的是物体相对于某个参考坐标系的朝向或旋转状态,通常以不同的轴(例如&#x…...
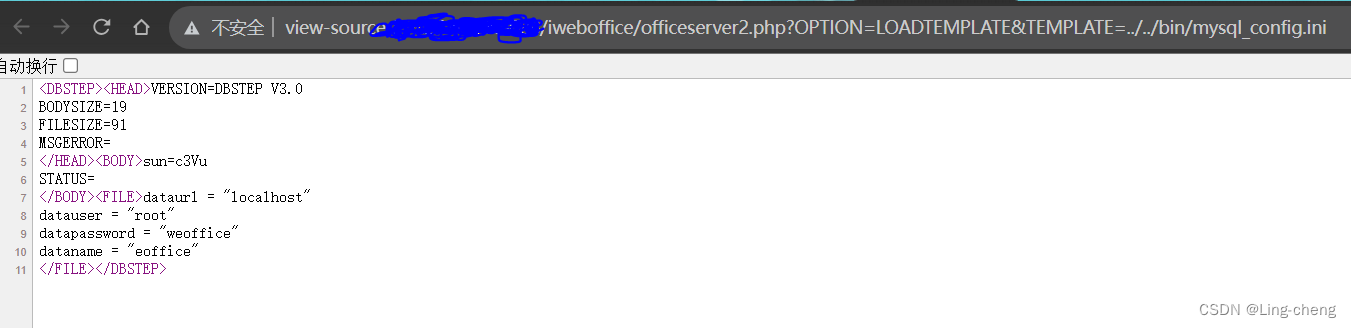
E-Office(泛微OA)前台任意文件读取漏洞复现
简介 泛微E-Office是一款企业级的全流程办公自动化软件,它包括协同办公、文档管理、知识管理、工作流管理等多个模块,涵盖了企业日常工作中的各个环节。在该产品前台登录页存在文件读取漏洞。 officeserver.php文件存在任意文件读取漏洞,通…...

前端小案例 | 喵喵大王立大功 | 一个带便利贴功能的todolist面板
文章目录 📚html📚css📚js🐇stickynote.js🐇todolist.js🐇clock.js 📚html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><m…...

算法训练营第十一天 | 20. 有效的括号、 1047. 删除字符串中的所有相邻重复项、150. 逆波兰表达式求值
目录: 力扣 20. 有效的括号力扣 1047. 删除字符串中的所有相邻重复项力扣 150. 逆波兰表达式求值 问题一、 20. 有效的括号 题目链接:20. 有效的括号 - 力扣(LeetCode) 思路分析: 很多朋友刚开始接触这一类题的时候…...
Python unittest单元测试框架 TestSuite测试套件
TestSuite 测试套件简介 对一个功能的验证往往是需要很多多测试用例,可以把测试用例集合在一起执行,这就产生了测试套件TestSuite 的概念,它是用来组装单个测试用例,规定用例的执行的顺序,而且TestSuite也可以嵌套Tes…...

FSB逮捕为乌克兰网络部队工作的俄罗斯黑客
导语 近日,俄罗斯联邦安全局(FSB)逮捕了两名涉嫌协助乌克兰网络部队对俄罗斯重要基础设施目标进行网络攻击的个人。这起事件引起了广泛关注,涉及到了网络安全和国际关系等多个领域。本文将为您详细介绍这一事件的背景和最新进展。…...
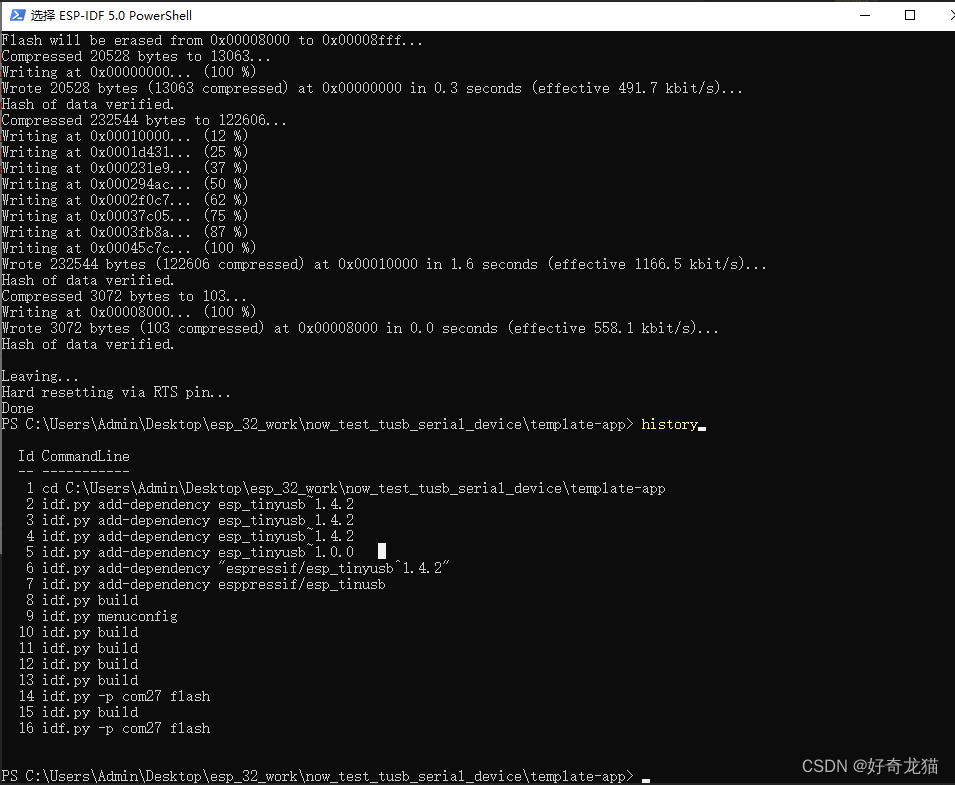
【PC电脑windows-学习样例tusb_serial_device-ESP32的USB模拟串口程序+VScode建立工程+usb组件添加+-基础样例学习】
【PC电脑windows-学习样例tusb_serial_device-ESP32的USB模拟串口程序-基础样例学习】 1、概述2、实验环境3-1、 物品说明3-2、所遇问题:ESP32 cannot open source file "tinyusb.h"或者“tinyusb.h:No such file or directory ....”3-3、解决问题&#…...

LeetCode75——Day26
文章目录 一、题目二、题解 一、题目 394. Decode String Given an encoded string, return its decoded string. The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guar…...
面试算法53:二叉搜索树的下一个节点
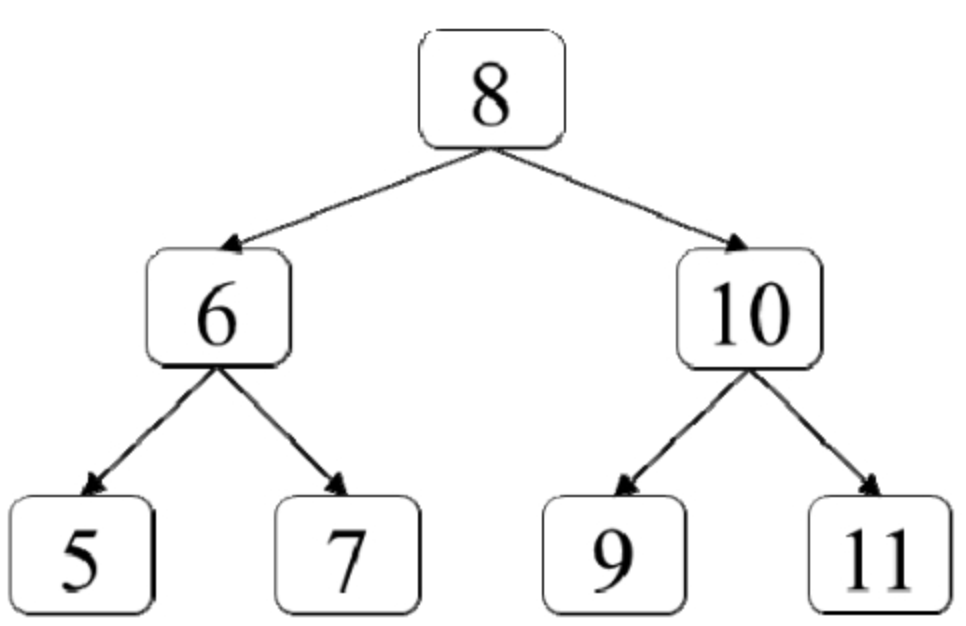
题目 给定一棵二叉搜索树和它的一个节点p,请找出按中序遍历的顺序该节点p的下一个节点。假设二叉搜索树中节点的值都是唯一的。例如,在图8.9的二叉搜索树中,节点8的下一个节点是节点9,节点11的下一个节点是null。 分析…...

2023SHCTF web方向wp
1.ezphp 看一眼,你大爷,啥玩意都给我过滤完了。 还好下面有preg_replace()/e,会把replacement当作php语句执行 传参pattern.*, .*表示任意字符,code{${phpinfo()}} ,为什么这样写,因为,print_…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
