基于树 二叉树的回溯搜索算法(DPLL)
1)全称:Davis-Putnam-Logemann-Loveland
2)思想:基于树/二叉树的回溯搜索算法,主要基于两种策略。
- 单子句规则:如果一个CNF范式中存在单子句L(含有一个文字的子句),取L为真值。通过L的值,遍历其他的子句:
如果某个子句中含有L,则将这个子句从范式中去掉(子句没了)
如果某个子句中含有-L(L的非),则将-L从这个子句中去掉(文字没了)
处理完之后,如果范式为空,则该范式为真;如果范式中含有空子句,则该范式为假。 - 分裂策略:如果一个范式S中不存在单子句。则按照某种方式选取一个变元v,假设v为真值和假值,然后重复单子句规则。(算法的复杂度和是否高效取决于选择变元的策略)
//伪代码:
bool DPLL(范式S){while(S中有单子句L){for(子句P in S){if(P中有L) 去掉P;else if(P中有-L) 去掉-L;}for循环执行完毕之后,S化简为S1if(S1 为空) return TRUE;else if(S1 中含有空子句) return FLASE;}按照某种策略选择变元v;if(DPLL(S∪v)) return TRUE;//递归回溯部分else return DPLL(S∪-v);
}
注意:既然是递归算法,自然要注意几个重要的点。其中有一个就是要记得你写的递归是否需要回溯。如果需要回溯,那些中间变量以及标记变量都需要及时回溯。(在传指针的时候尤其需要注意!!!)
相关文章:
)
基于树 二叉树的回溯搜索算法(DPLL)
1)全称:Davis-Putnam-Logemann-Loveland 2)思想:基于树/二叉树的回溯搜索算法,主要基于两种策略。 单子句规则:如果一个CNF范式中存在单子句L(含有一个文字的子句),取L为…...

【嵌入式】适用于ESP32/ESP8266远程自动烧录工具
文章目录 介绍开始使用下载项目开启服务端开始远程烧录 后记 介绍 esp_remote_flash_tool 是一款基于 esptool.py 的远程自动烧录工具,支持 ESP32 和 ESP8266。 使用场景 基于 ESP-IDF 、ESP8266 NONO SDK、ESP8266 RTOS SDK 进行开发的项目项目代码存储在 Linux…...
服务器遭受攻击如何处理(记录排查)
本文的重点是介绍如何鉴别安全事件以及保护现场的方法,以确保服务器负责人能够在第一时间对安全攻击做出反应,并在最短时间内抵御攻击或减少攻击所带来的影响。 在服务器遭遇疑似安全事件时,通常可以从账号、进程、网络和日志四个主要方面进…...

分享81个工作总结PPT,总有一款适合您
分享81个工作总结PPT,总有一款适合您 PPT下载链接:https://pan.baidu.com/s/13hyrlZo2GhRoQjI-6z31-w?pwd8888 提取码:8888 Python采集代码下载链接:采集代码.zip - 蓝奏云 学习知识费力气,收集整理更不易。知识付…...
什么是DITA?从百度的回答说起
▲ 搜索“大龙谈智能内容”关注GongZongHao▲ 什么是DITA? 把这个问题输入百度,获得以下回答: DITA 是“Darwin Information Typing Architecture”(达尔文信息类型化体系结构)的缩写,它是IBM 公司为OASIS 所支持…...
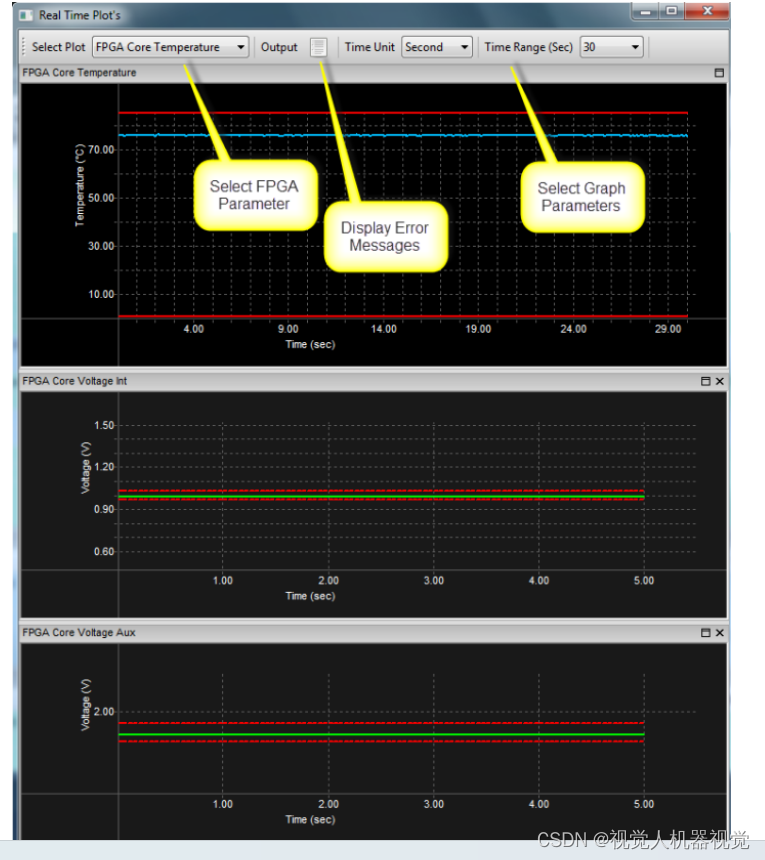
线扫相机DALSA软件开发套件有哪些
Win10和Win7系统完整SDK目录截图: Sapera Configuration 缓存与内存管理,以及通信端口配置工具,部分功能等效于Detection(查找相机)内的Settings。 Sapera Log Viewer 打开Log Viewer后会显示之前发生过的所有与Sapera LT软件有关的运行信息…...
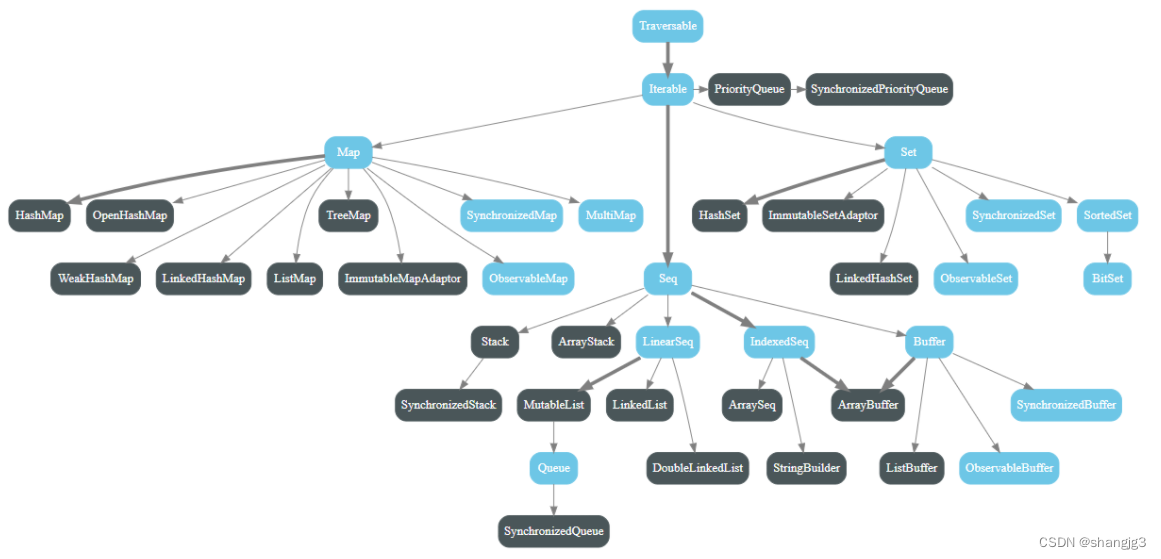
Scala集合操作
1 集合简介 Scala 中拥有多种集合类型,主要分为可变的和不可变的集合两大类: 可变集合: 可以被修改。即可以更改,添加,删除集合中的元素; 不可变集合类:不能被修改。对集合执行更改,…...

SQL备忘--特殊状态“未知“以及“空值NULL“的判断
一、新逻辑状态:未知 对于大多数其他语言的逻辑判断,一般只有两种结果:真(TURE)或假(FALSE)但在SQL中,还会有第三种判断结果:未知(UNKNOWN),表示无法判断出真或者假。 未知状态会影响传统逻辑运算&#x…...
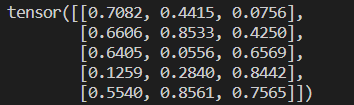
《Pytorch新手入门》第一节-认识Tensor
《Pytorch新手入门》第一节-认识Tensor 一、认识Tensor1.1 Tensor定义1.2 Tensor运算操作1.3 Tensor与numpy转换 参考《深度学习框架PyTorch:入门与实践_陈云(著)》 一、认识Tensor 1.1 Tensor定义 Tensor 是 PyTorch 中重要的数据结构,可认为是一个高…...
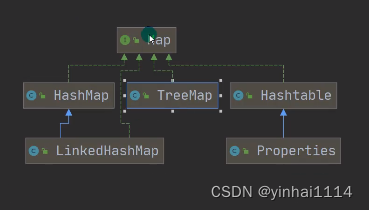
【JAVA学习笔记】55 - 集合-Map接口、HashMap类、HashTable类、Properties类、TreeMap类(难点)
项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter14/src/com/yinhai/map_ Map接口 一、Map接口的特点(难点) 难点在于对Node和Entry和EntrySet的关系 注意:这里讲的是JDK8的Map接口特点 Map java 1) Map与Collect…...

Pytorch图像模型转ONNX后出现色偏问题
本篇记录一次从Pytorch图像处理模型转换成ONNX模型之后,在推理过程中出现了明显色偏问题的解决过程。 问题描述:原始pytorch模型推理正常,通过torch.onnx.export()函数转换成onnx之后,推理时出现了比较明显的颜色偏差。 原始模型…...

插值表达式 {{}}
前言 持续学习总结输出中,今天分享的是插值表达式 {{}} Vue插值表达式是一种Vue的模板语法,我们可以在模板中动态地用插值表达式渲染出Vue提供的数据绑定到视图中。插值表达式使用双大括号{{ }}将表达式包裹起来。 1.作用: 利用表达式进行…...

白雪公主
前言 #define 皇后 王后 在很久很久以前,有一个国王,由于王后难产致死,导致生下的孩子没母,由于缺爱,变的非常的刻薄 由于公主过于刻薄,以至于见到她的人都面色煞白感到空中飘雪 37C 的嘴怎能说出如此刻薄的话语。为了…...

宏观角度认识递归之合并两个有序链表
21. 合并两个有序链表 - 力扣(LeetCode) 依旧是利用宏观角度来看待问题,其中最主要的就是要找到重复的子问题; 题目中要求把两个有序链表进行合并,同时不能够创建新的节点,并返回链表的起始点:因…...

Leetcode-509 斐波那契数列
使用循环 class Solution {public int fib(int n) {if(n 0){return 0;}if(n 1){return 1;}int res 0;int pre1 1;int pre2 0;for(int i 2; i < n; i){res pre1 pre2;pre2 pre1;pre1 res;}return res;} }使用HashMap class Solution {private Map<Integer,Int…...

解密 docker 容器内 DNS 解析原理
背景 这几天在使用 docker 中,碰到了在容器中 DNS 解析的一些问题。故花些时间弄清了原理,写此文章分享。 1. docker run 命令启动的容器 以启动一个 busybox 容器为例: rootubuntu20:~# docker run -itd --name u1 busybox 63b59ca8aeac…...
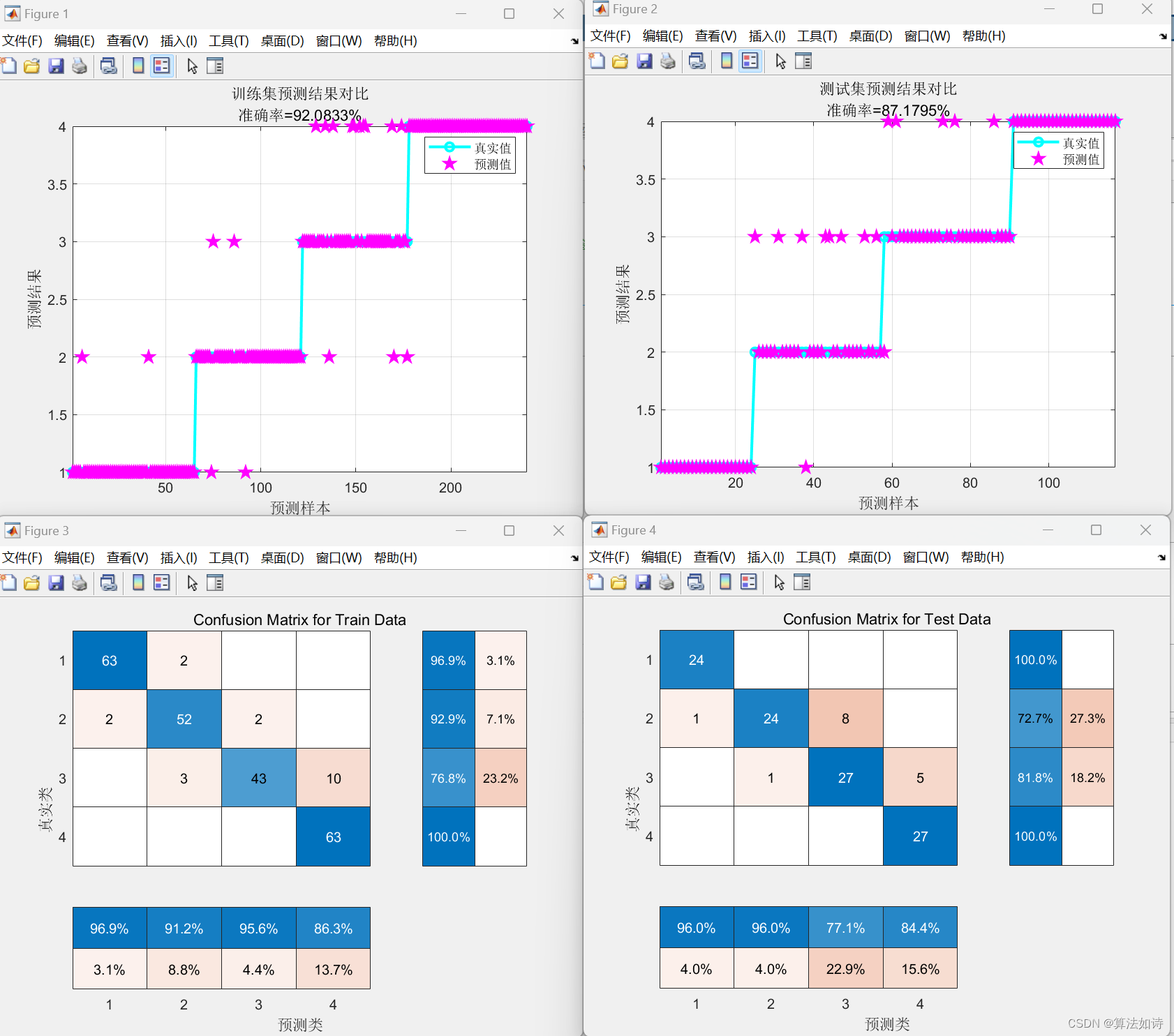
故障诊断模型 | Maltab实现SVM支持向量机的故障诊断
效果一览 文章概述 故障诊断模型 | Maltab实现SVM支持向量机的故障诊断 模型描述 Chinese: Options:可用的选项即表示的涵义如下 -s svm类型:SVM设置类型(默认0) 0 – C-SVC 1 --v-SVC 2 – 一类SVM 3 – e -SVR 4 – v-SVR -t 核函数类型:核函…...

开源的网站数据分析统计平台——Matomo
Matomo 文章目录 Matomo前言一、环境准备1. 整体安装流程2.安装PHP 7.3.303.nginx配置4.安装matomo4.1 访问安装页面 http://192.168.10.45:8088/index.php4.2 连接数据库4.3 设置管理员账号4.4 生成js跟踪代码4.5 安装完成4.6 警告修改4.7 刷新页面,就可以看到登陆…...
linux入门到地狱
linux—001入门 IT圈必备(前端工作者用的比较少) 老旧电脑跑linux不容易卡 我代码没保存windows闪退,僵停(vs2019卡掉线),重启更新,占用cpu内存服务报错pip各种bug 出来生态环境友好其他的全是bug(bug时间成本超过了windows快捷友好生态) 那就说明wind…...
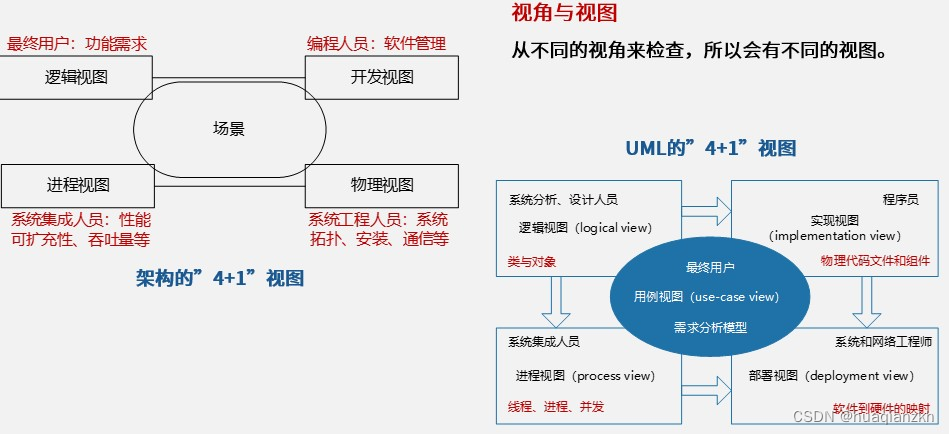
架构”4+1“视图
1995年Kruchten提出了著名的“41”视图,用来描述软件系统的架构。在“41”视图中,(物理视图 )用来描述系统软硬件之间的映射关系,这个视图往往(系统工程人员)最为关注;(逻…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
