pytorch-损失函数-分类和回归区别
torch.nn 库和 torch.nn.functional库的区别
-
torch.nn库:这个库提供了许多预定义的层,如全连接层(Linear)、卷积层(Conv2d)等,以及一些损失函数(如MSELoss、CrossEntropyLoss等)。这些层都是类,它们都继承自nn.Module,因此可以很方便地集成到自定义的模型中。torch.nn库中的层都有自己的权重和偏置,这些参数可以通过优化器进行更新。-
当你需要的操作包含可学习的参数(例如权重和偏置)时,通常使用
torch.nn库更为方便。例如,对于卷积层(Conv2d)、全连接层(Linear)等,由于它们包含可学习的参数,因此通常使用torch.nn库中的类。这些类会自动管理参数的创建和更新。例如:
-
import torch.nn as nnconv = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, stride=1, padding=1) fc = nn.Linear(in_features=1024, out_features=10)
-
-
torch.nn.functional库:这个库提供了一些函数,如激活函数(如relu、sigmoid等)、池化函数(如max_pool2d、avg_pool2d等)以及一些损失函数(如cross_entropy、mse_loss等)。这些函数更加灵活,但使用它们需要手动管理权重和偏置。
-
对于没有可学习参数的操作,例如ReLU激活函数、池化操作、dropout等,你可以选择使用torch.nn.functional库,因为这些操作不需要额外的参数。
-
import torch.nn.functional as Fx = F.relu(x) x = F.max_pool2d(x, kernel_size=2) x = F.dropout(x, p=0.5, training=self.training)
-
-
对于损失函数,torch.nn库和torch.nn.functional库都提供了实现,你可以根据需要选择。如果你需要的损失函数有可学习的参数(例如nn.BCEWithLogitsLoss中的pos_weight),那么应该使用torch.nn库。如果你的损失函数没有可学习的参数,那么你可以选择使用torch.nn.functional库,这样可以避免创建不必要的对象。
例如:
-
import torch.nn as nn import torch.nn.functional as F# 使用nn库 loss_fn = nn.CrossEntropyLoss() loss = loss_fn(prediction, target)# 使用functional库 loss = F.cross_entropy(prediction, target)
torch.nn 库和 torch.nn.functional库损失函数的对应关系
以下是一些常见的损失函数在torch.nn和torch.nn.functional中的对应关系:
- 交叉熵损失:
- torch.nn.CrossEntropyLoss
- torch.nn.functional.cross_entropy
- 负对数似然损失:
- torch.nn.NLLLoss
- torch.nn.functional.nll_loss
- 均方误差损失:
- torch.nn.MSELoss
- torch.nn.functional.mse_loss
- 平均绝对误差损失:
- torch.nn.L1Loss
- torch.nn.functional.l1_loss
分类和回归损失函数的区别
- 分类问题:分类问题的目标是预测输入数据的类别。对于这类问题,常用的损失函数有交叉熵损失(Cross Entropy Loss)和负对数似然损失(Negative Log Likelihood Loss)。这些损失函数都是基于预测的概率分布和真实的概率分布之间的差异来计算损失的。
- nn.CrossEntropyLoss:这是用于分类问题的损失函数。它期望的输入是一个形状为(batch_size, num_classes)的张量,其中每个元素是对应类别的原始分数(通常是最后一个全连接层的输出),以及一个形状为(batch_size,)的张量,其中每个元素是真实的类别标签。
- nn.NLLLoss:这也是用于分类问题的损失函数。它期望的输入是一个形状为(batch_size, num_classes)的张量,其中每个元素是对应类别的对数概率(通常是log_softmax的输出),以及一个形状为(batch_size,)的张量,其中每个元素是真实的类别标签。
- 回归问题:回归问题的目标是预测一个连续的值。对于这类问题,常用的损失函数有均方误差损失(Mean Squared Error Loss)和平均绝对误差损失(Mean Absolute Error Loss)。这些损失函数都是基于预测值和真实值之间的差异来计算损失的。
- nn.MSELoss:这是用于回归问题的损失函数。它期望的输入是两个形状相同的张量,一个是预测值,一个是真实值。这两个张量的形状可以是任意的,只要它们相同即可。
- nn.L1Loss:这也是用于回归问题的损失函数。它期望的输入是两个形状相同的张量,一个是预测值,一个是真实值。这两个张量的形状可以是任意的,只要它们相同即可。
举例说明
nn.MSELoss()
输入:预测值和目标值,它们的形状应该是相同的。例如,如果你有一个批量大小为batch_size的数据,每个数据有n个特征,那么预测值和目标值的形状都应该是(batch_size, n)。
输出:一个标量,表示计算得到的均方误差损失。
例如:
import torch
import torch.nn as nn# 假设我们有一个批量大小为3的数据,每个数据有2个特征
prediction = torch.randn(3, 2)
target = torch.randn(3, 2)loss_fn = nn.MSELoss()
loss = loss_fn(prediction, target)print(loss) # 输出一个标量,表示计算得到的均方误差损失
F.cross_entropy()
输入:预测值和目标值。预测值的形状应该是(batch_size, num_classes),表示对每个类别的预测概率;目标值的形状应该是(batch_size,),表示每个数据的真实类别标签。
输出:一个标量,表示计算得到的交叉熵损失。
例如:
import torch
import torch.nn.functional as F# 假设我们有一个批量大小为3的数据,有4个类别
prediction = torch.randn(3, 4)
target = torch.tensor([1, 0, 3]) # 真实的类别标签loss = F.cross_entropy(prediction, target)print(loss) # 输出一个标量,表示计算得到的交叉熵损失
多分类中CrossEntropyLoss() 和NLLLoss()的区别
- CrossEntropyLoss():它的输入是模型对每个类别的原始分数(通常是最后一个全连接层的输出),并且这些分数没有经过任何归一化处理。CrossEntropyLoss()内部会对这些分数进行log_softmax操作,然后计算交叉熵损失。
- NLLLoss():它的输入是模型对每个类别的对数概率,这些对数概率通常是通过对模型的原始输出进行log_softmax操作得到的。NLLLoss()会直接计算负对数似然损失。
CrossEntropyLoss() = softmax + log + NLLLoss() = log_softmax + NLLLoss()
二分类中BCELoss和BCEWithLogitsLoss的区别
BCELoss()和BCEWithLogitsLoss()都是PyTorch中常用的损失函数,主要用于二分类问题。但是它们的输入和处理方式有所不同。
- BCELoss():它的输入是模型对每个类别的概率,这些概率通常是通过对模型的原始输出进行sigmoid操作得到的。BCELoss()会直接计算二元交叉熵损失。
- BCEWithLogitsLoss():它的输入是模型对每个类别的原始分数(通常是最后一个全连接层的输出),并且这些分数没有经过任何归一化处理。BCEWithLogitsLoss()内部会对这些分数进行sigmoid操作,然后计算二元交叉熵损失。
总的来说,BCELoss()和BCEWithLogitsLoss()的主要区别在于它们的输入:BCELoss()期望的输入是模型的概率输出,而BCEWithLogitsLoss()期望的输入是模型的原始输出。在实际使用中,你可以根据自己的需求和模型的输出来选择使用哪一个损失函数。
另外,BCEWithLogitsLoss()在内部进行sigmoid和loss计算可以提高数值稳定性,因此在实际使用中,如果模型的输出是原始分数,推荐使用BCEWithLogitsLoss()。
回归损失函数中的reduction函数详解
它的完整定义是torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')。
下面是这些参数的解释:
- size_average(已弃用):如果设置为True,损失函数会对每个小批量的损失取平均值。如果设置为False,损失函数会对每个小批量的损失求和。默认值是True。这个参数已经被弃用,推荐使用reduction参数。
- reduce(已弃用):如果设置为True,损失函数会返回一个标量值,即所有输入元素的损失的平均值或总和(取决于size_average参数)。如果设置为False,损失函数会返回一个损失值的向量,每个元素对应一个输入数据点的损失。默认值是True。这个参数已经被弃用,推荐使用reduction参数。
- reduction:指定如何减少损失。可以是'none'(不减少,返回一个损失值的向量),'mean'(取平均,返回所有输入元素的损失的平均值)或'sum'(求和,返回所有输入元素的损失的总和)。默认值是'mean'。
nn.MSELoss()函数的输入是两个张量,分别代表预测值和目标值。它们必须有相同的形状。函数的输出是一个标量值,表示损失。
nn.SmoothL1Loss相比于nn.MSELoss损失函数的优点
- nn.MSELoss(均方误差损失)对于回归问题非常有效,但它对于异常值(outliers)非常敏感,因为它会将每个误差的平方进行求和。这意味着,即使只有一个样本的预测值与真实值相差很大,也会导致整体损失值显著增加。
- 而nn.SmoothL1Loss(平滑L1损失)则在处理异常值时更为鲁棒。它结合了L1损失和L2损失的优点:当预测值与真实值的差距较大时,它的行为类似于L1损失(即绝对值损失),对异常值不敏感;而当预测值与真实值接近时,它的行为类似于L2损失(即均方误差损失),可以更精细地优化模型。
因此,nn.SmoothL1Loss的一个主要优点是它可以在处理异常值和进行精细优化之间找到一个平衡,这在某些任务中可能是非常有用的。
nn.SmoothL1Loss是通过一个特定的数学公式来实现这个优点的。这个公式如下:
SmoothL1Loss(x, y) = 0.5 * (x - y)^2, if abs(x - y) < 1= abs(x - y) - 0.5, otherwise
这个公式的含义是,当预测值和真实值的差距小于1时,使用平方误差损失(即L2损失);当差距大于或等于1时,使用绝对值误差损失(即L1损失)。
可以看到,当差距较小的时候,SmoothL1Loss的行为类似于nn.MSELoss,它会对这些小的误差进行精细优化。而当差距较大的时候,SmoothL1Loss的行为类似于L1损失,它不会对这些大的误差进行过度惩罚,从而提高了对异常值的鲁棒性。
这就是nn.SmoothL1Loss如何在处理异常值和进行精细优化之间找到平衡的。
nn.HuberLoss的作用
nn.HuberLoss也被称为Huber损失,是一种结合了均方误差损失(Mean Squared Error,MSE)和平均绝对误差损失(Mean Absolute Error,MAE)的损失函数。它在处理回归问题时,尤其是存在异常值(outliers)的情况下,表现出较好的性能。
Huber损失的计算公式如下:
HuberLoss(x, y) = 0.5 * (x - y)^2, if abs(x - y) < delta= delta * abs(x - y) - 0.5 * delta^2, otherwise
这个公式的含义是,当预测值和真实值的差距小于一个阈值delta时,使用平方误差损失(即MSE);当差距大于或等于delta时,使用线性误差损失(即MAE)。
与nn.SmoothL1Loss类似,nn.HuberLoss在处理异常值和进行精细优化之间找到了一个平衡。当预测误差较小的时候,它的行为类似于MSE,可以对这些小的误差进行精细优化;而当预测误差较大的时候,它的行为类似于MAE,不会对这些大的误差进行过度惩罚,从而提高了对异常值的鲁棒性。
另外,nn.HuberLoss的一个优点是它的梯度在整个定义域内都是有界的,这使得模型在训练过程中更稳定。
参考自:
pytorch中常用的损失函数用法说明 | w3cschool笔记
pytorch教程 (四)- 损失函数_pytorch对比损失-CSDN博客
相关文章:

pytorch-损失函数-分类和回归区别
torch.nn 库和 torch.nn.functional库的区别 torch.nn库:这个库提供了许多预定义的层,如全连接层(Linear)、卷积层(Conv2d)等,以及一些损失函数(如MSELoss、CrossEntropyLoss等&…...
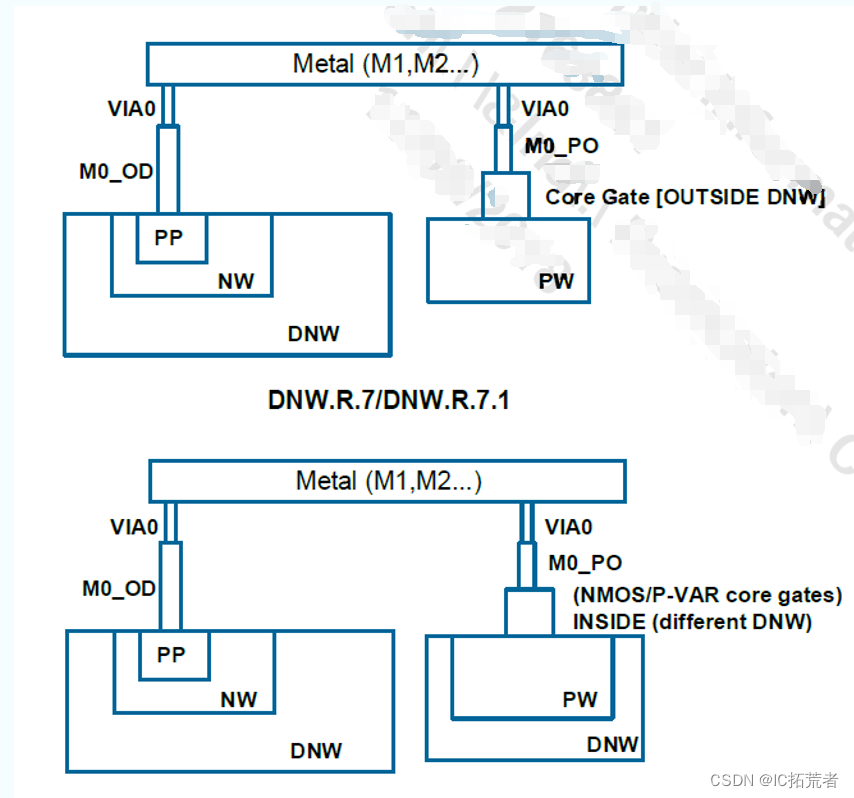
数字IC后端实现 |TSMC 12nm 与TSMC 28nm Metal Stack的区别
下图为咱们社区IC后端训练营项目用到的Metal Stack。 芯片Tapeout Review CheckList 数字IC后端零基础入门Innovus学习教程 1P代表一层poly,10M代表有10层metal,M5x表示M2-M6为一倍最小线宽宽度的金属层,2y表示M7-M8为二倍最小线宽宽度的金…...
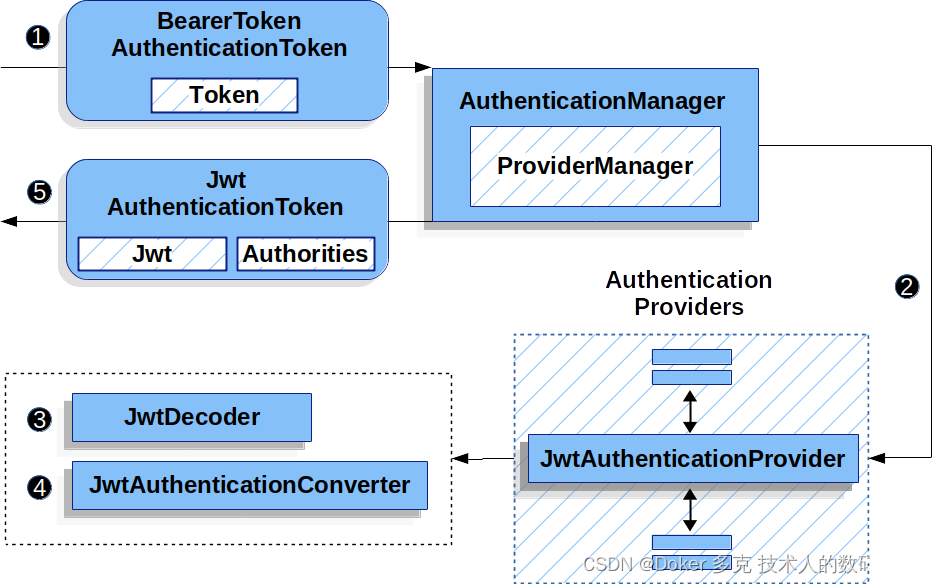
Spring Security OAuth 2.0 资源服务器— JWT
目录 一、JWT的最小依赖 二、JWT的最基本配置 1、指定授权服务器 2、初始预期(Startup Expectations) 3、运行时预期(Runtime Expectations) 三、JWT认证是如何工作的 四、直接指定授权服务器 JWK Set Uri 五、提供 audie…...

C++初阶(八)类和对象
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、Static成员1、Static概念2、Static特性3、试题 二、友元1、友元的类型2、友元函数3、 友元…...
Excel文档名称批量翻译的高效方法
在处理大量文件时,我们常常需要借助一些工具来提高工作效率。例如,在需要对Excel文档名称进行批量翻译时,一个方便快捷的工具可以帮助我们省去很多麻烦。今天,我将介绍一款名为固乔文件管家的软件,它能够帮助我们轻松实…...

python里面的浅拷贝和深拷贝
目录 浅拷贝(Shallow Copy):深拷贝(Deep Copy):实现方式:使用copy模块进行拷贝:使用切片(只适用于列表和其他序列类型)进行浅拷贝:使用list()、di…...
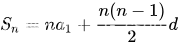
HJ76 尼科彻斯定理
题目: HJ76 尼科彻斯定理 题解: m个连续奇数之和,所以我们只要求出连续奇数的第一位就能以此枚举所有奇数,连续奇数是一个等差数列。 S m^3, n m, d 2 > a1 m^2 - (m-1) import java.util.Scanner;// 注意类名必须…...

AndroidAuto PCTS A118解决杂音问题
A118最后播放三段media类型音频数据,中间会有一点beep的杂音,这个是暂停跟播放没有衔接好导致的,解决这个问题的思路是要分离开播放跟暂停,不能还没完全暂停就播放下一段音频数据 修改点在AudioPlayer.java @Overridepublic synchronized void onStart(int sessionId) {if …...

uniapp小程序砸金蛋抽奖
砸之前是金蛋png图片,点击砸完之后切换砸金蛋动效gif图片; 当前代码封装为砸金蛋的组件; vue代码: <template><view class"page" v-if"merchantInfo.cdn_static"><image class"bg&qu…...
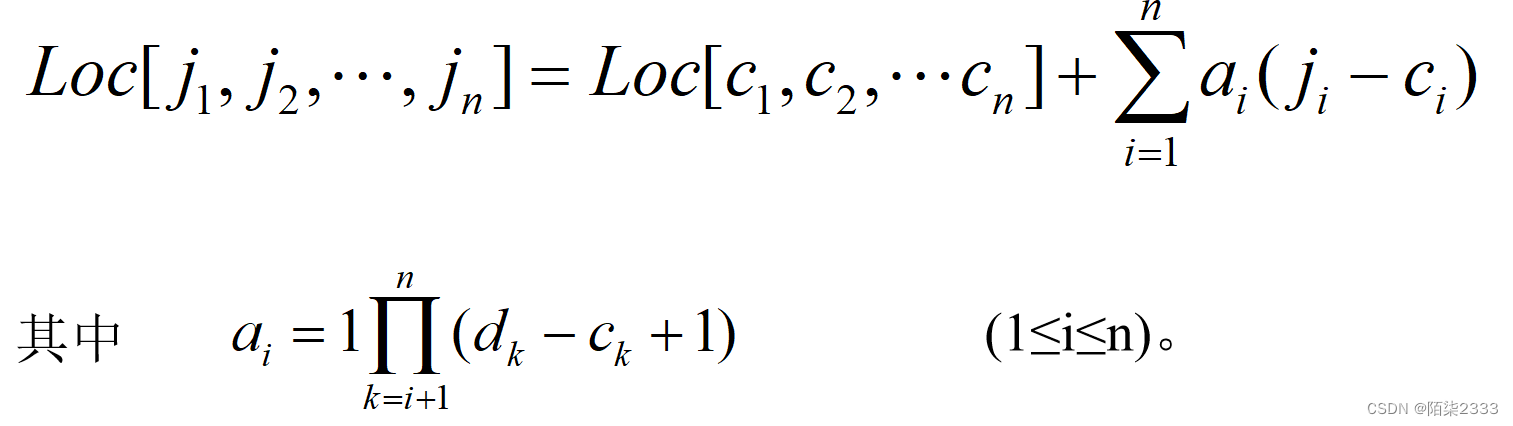
数据结构(超详细讲解!!)第二十节 数组
1.定义 1.概念 相同类型的数据元素的集合。 记作:A(A0,A1,…,Am-1) 二维数组可看作是每个数据元素都是相同类型的一维数组的一维数组。多维数组依此类推。 二维数组是数据元素为线性表的线性表。 A(A0,A1,……,An-1) 其中…...

【Android】Android Framework系列---CarPower深度睡眠STR
Android Framework系列—CarPower深度睡眠 之前博客说了CarPower的开机启动流程 这里分析一下,Android CarPower实现深度睡眠的流程。 首先,什么是深度睡眠(Deep Sleep)? Android进入Deep Sleep后,关闭屏幕、关闭CPU的电源,保持…...
【漏洞复现】Fastjson_1.2.47_rce
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞检测3、漏洞验证 1.5、深度利用1、反弹Shell 说明内容漏洞编号漏洞名称Fastjson_1.2.47_远程执行漏…...

玩转AIGC:如何选择最佳的Prompt提示词?
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

ELK搭建以及使用教程(多pipiline)
1、环境准备 服务器:Centos7 Jdk版本:1.8 Es版本:7.12.1 kibana版本:7.12.1 logstash版本:7.12.1 IP地址安装软件192.168.50.211Es,Kibana,logstash 2、安装docker 安装步骤参考:https:…...

小程序如何设置用户同意服务协议并上传头像和昵称
为了保护用户权益和提供更好的用户体验,设置一些必填项和必读协议是非常必要的。首先,用户必须阅读服务协议。服务协议是明确规定用户和商家之间权益和义务的文件。通过要求用户在下单前必须同意协议,可以确保用户在使用服务之前了解并同意相…...

6.4 例程:使用互斥量
这个例程为使用多线程配合互斥量进行点乘计算,相关的数据通过全局变量的形式存在,因此可以被各个线程访问;每个线程会在相关数据的不同区域上进行处理,主线程等待子线程完成操作后,将最后的结果打印出来。 代码如下 #…...
)
[算法日志]图论: 深度优先搜索(DFS)
[算法日志]图论: 深度优先搜索(DFS) 深度优先概论 深度优先搜索算法是一种遍历图这种数据结构的算法策略,其中心思想是朝图节点的一个方向不断跳转,当该节点无下一个节点或所有方向都遍历完时,便回溯朝上一个节点的另一个方向…...

这道经典SQL面试问题你会吗?
大家经常自嘲后端开发就是crud boy嘛,今天给大家看一道SQL题,我相信很多人写不出来。我们来看一下这个题目。 create table course (id int primary key,name varchar(32) not null ); create table student (id int primary key,name varchar(32) not …...

网络服务退出一个问题的解析
一、问题 在实际开发中遇到一个问题,解决的过程虽然不长,但确实是想得比较多,总结一下,以供参考。这是一个网络通信的服务端而且使用的是别人封装好的库,通信等都没有问题,但在退出时会报一个错误…...

第四次pta认证P测试
第一题 试题编号: 试题名称:整数排序 时间限制: 1.0s 内存限制: 128.0MB 【问题描述】 老师给定 10 个整数的序列,要求对其重新排序。排序要求: 1.奇数在前,偶数在后; 2.奇数按从大到小排序&am…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...
