《视觉SLAM十四讲》-- 三维空间的刚体运动
文章目录
- 02 三维空间的刚体运动
- 2.0 机器人位姿表述
- 2.1 点和坐标系
- 2.1.1 三维坐标系有关表述
- 2.1.2 坐标系变换
- 2.2 旋转向量和欧拉角
- 2.2.1 旋转向量
- 2.2.2 欧拉角
- 2.3 四元数
- 2.3.1 四元数的定义
- 2.3.2 四元数的计算
- 2.3.3 四元数表示旋转
- 2.3.4 四元数与其他旋转表示法的转换
- 2.4 相似、仿射、射影变换
02 三维空间的刚体运动
2.0 机器人位姿表述
(1)二维与三维空间中,机器人位姿的表述:
-
2D 的情况:横纵坐标 + 旋转角(机器人朝向),即 [ x , y , θ ] [x, y, \theta] [x,y,θ]
-
3D 的情况:三维空间中的旋转和平移
2.1 点和坐标系
2.1.1 三维坐标系有关表述
(1)基本运算
-
加减法
-
内积(点乘): a ⋅ b = a T b = ∑ i = 1 3 a i × b i = ∣ a ∣ ∣ b ∣ c o s < a , b > \boldsymbol{a}\cdot\boldsymbol{b}=\boldsymbol{a}^T\boldsymbol{b}=\sum_{i=1}^{3}a_{i}\times b_{i} = |\boldsymbol{a}| |\boldsymbol{b}|cos<\boldsymbol{a}, \boldsymbol{b}> a⋅b=aTb=∑i=13ai×bi=∣a∣∣b∣cos<a,b>,且 a ⋅ b = b ⋅ a \boldsymbol{a}\cdot\boldsymbol{b} = \boldsymbol{b}\cdot\boldsymbol{a} a⋅b=b⋅a
-
外积(叉乘):
a × b = ∥ e 1 e 2 e 3 a 1 a 2 a 3 b 1 b 2 b 3 ∥ = ( a 2 b 3 − a 3 b 2 ) e 1 + ( a 3 b 1 − a 1 b 3 ) e 2 + ( a 1 b 3 − a 3 b 1 ) e 3 = [ a 2 b 3 − a 3 b 2 a 3 b 1 − a 1 b 3 a 1 b 2 − a 2 b 1 ] = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] b = def a ∧ b (2-1) \begin{aligned} \boldsymbol{a} \times \boldsymbol{b}=\left\|\begin{array}{ccc} \boldsymbol{e}_{1} & \boldsymbol{e}_{2} & \boldsymbol{e}_{3} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{array}\right\| &=(a_2b_3-a_3b_2)\boldsymbol{e}_{1}+(a_3b_1-a_1b_3)\boldsymbol{e}_{2}+(a_1b_3-a_3b_1)\boldsymbol{e}_{3} \\ &=\left[\begin{array}{c} a_{2} b_{3}-a_{3} b_{2} \\ a_{3} b_{1}-a_{1} b_{3} \\ a_{1} b_{2}-a_{2} b_{1} \end{array}\right]=\left[\begin{array}{ccc} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{array}\right] \boldsymbol{b}\stackrel{\text { def }}{=}\boldsymbol{a}^{\wedge} \boldsymbol{b} \end{aligned} \tag{2-1} a×b= e1a1b1e2a2b2e3a3b3 =(a2b3−a3b2)e1+(a3b1−a1b3)e2+(a1b3−a3b1)e3= a2b3−a3b2a3b1−a1b3a1b2−a2b1 = 0a3−a2−a30a1a2−a10 b= def a∧b(2-1)
也即 a × b = ∣ a ∣ ∣ b ∣ s i n < a , b > \boldsymbol{a} \times \boldsymbol{b} = |\boldsymbol{a}| |\boldsymbol{b}|sin<\boldsymbol{a}, \boldsymbol{b}> a×b=∣a∣∣b∣sin<a,b>,方向垂直于向量 a \boldsymbol{a} a、 b \boldsymbol{b} b 组成的平面,遵循右手定则。
性质: a × b = − b × a \boldsymbol{a} \times \boldsymbol{b} = - \boldsymbol{b} \times \boldsymbol{a} a×b=−b×a
为便于后续表达,记
a ∧ = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] (2-2) \boldsymbol{a}^{\wedge}=\left[\begin{array}{ccc} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{array}\right] \tag{2-2} a∧= 0a3−a2−a30a1a2−a10 (2-2)
这是一个反对称矩阵,满足 A T = − A A^T=-A AT=−A。
2.1.2 坐标系变换
(1)三维空间向量表示:
a = [ e 1 , e 2 , e 3 ] [ a 1 a 2 a 3 ] = a 1 e 1 + a 2 e 2 + a 3 e 3 (2-3) \boldsymbol{a}=\left[\boldsymbol{e_1},\boldsymbol{e_2},\boldsymbol{e_3}\right]\left[\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=a_1\boldsymbol{e_1}+a_2\boldsymbol{e_2}+a_3\boldsymbol{e_3} \tag{2-3} a=[e1,e2,e3] a1a2a3 =a1e1+a2e2+a3e3(2-3)
其中, e 1 、 e 2 、 e 3 \boldsymbol{e_1}、\boldsymbol{e_2}、\boldsymbol{e_3} e1、e2、e3为基向量。
(2)两个坐标系之间的运动由一个旋转加一个平移组成,这种运动称为刚体运动。
(3)对于坐标系旋转变换,假设原坐标系和现坐标系单位正交基底分别为 [ e 1 , e 2 , e 3 ] [\boldsymbol{e_1}, \boldsymbol{e_2}, \boldsymbol{e_3}] [e1,e2,e3]和 [ e 1 ′ , e 2 ′ , e 3 ′ ] [\boldsymbol{e_1'}, \boldsymbol{e_2'}, \boldsymbol{e_3'}] [e1′,e2′,e3′],
坐标分别为 [ a 1 , a 2 , a 3 ] T [a_1, a_2, a_3]^T [a1,a2,a3]T和 [ a 1 ′ , a 2 ′ , a 3 ′ ] T [a_1', a_2', a_3']^T [a1′,a2′,a3′]T,由于向量本身的绝对位置没有改变,则
[ e 1 , e 2 , e 3 ] [ a 1 a 2 a 3 ] = [ e 1 ′ , e 2 ′ , e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] (2-4) \left[\boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \boldsymbol{e}_{3}\right]\left[\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[\boldsymbol{e}_{1}^{\prime}, \boldsymbol{e}_{2}^{\prime}, \boldsymbol{e}_{3}^{\prime}\right]\left[\begin{array}{c} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right] \tag{2-4} [e1,e2,e3] a1a2a3 =[e1′,e2′,e3′] a1′a2′a3′ (2-4)
将上式两端分别左乘 [ e 1 T e 2 T e 3 T ] \left[\begin{array}{l} \boldsymbol{e_{1}^T} \\ \boldsymbol{e}_{2}^T \\ \boldsymbol{e}_{3}^T \end{array}\right] e1Te2Te3T 得到,
[ a 1 a 2 a 3 ] = [ e 1 T e 1 ′ e 1 T e 2 ′ e 1 T e 3 ′ e 2 T e 1 ′ e 2 T e 2 ′ e 2 T e 3 ′ e 3 T e 1 ′ e 3 T e 2 ′ e 3 T e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] = def R a ′ (2-5) \left[\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[\begin{array}{lll} \boldsymbol{e}_{1}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{1}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{1}^T \boldsymbol{e}_{3}^{\prime} \\ \boldsymbol{e}_{2}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{2}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{2}^T \boldsymbol{e}_{3}^{\prime} \\ \boldsymbol{e}_{3}^T \boldsymbol{e}_{1}^{\prime} & \boldsymbol{e}_{3}^T \boldsymbol{e}_{2}^{\prime} & \boldsymbol{e}_{3}^T \boldsymbol{e}_{3}^{\prime} \end{array}\right]\left[\begin{array}{c} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right] \stackrel{\text { def }}{=} \boldsymbol{R} \boldsymbol{a}^{\prime} \tag{2-5} a1a2a3 = e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′ a1′a2′a3′ = def Ra′(2-5)
矩阵 R \boldsymbol{R} R即为旋转矩阵。它有如下性质:
- R \boldsymbol{R} R 行列式为 1;
- R \boldsymbol{R} R 是一个正交矩阵,即满足 R T R = I \boldsymbol{R}^T\boldsymbol{R}=\boldsymbol{I} RTR=I。
- 坐标系 1 到坐标系 2 ,有 a 1 = R 12 a 2 \boldsymbol{a_1}=\boldsymbol{R_{12}}\boldsymbol{a_2} a1=R12a2,反之有 a 2 = R 21 a 1 \boldsymbol{a_2}=\boldsymbol{R_{21}}\boldsymbol{a_1} a2=R21a1,其中,
R 12 = R 21 − 1 = R 21 T \boldsymbol{R_{12}}=\boldsymbol{R_{21}}^{-1}=\boldsymbol{R_{21}}^T R12=R21−1=R21T
将满足此性质的矩阵集合定义为特殊正交群:
S O ( n ) = { R ∈ R n × n ∣ R R T = I , det ( R ) = 1 } (2-6) \mathrm{SO}(n)=\left\{\boldsymbol{R} \in \mathbb{R}^{n \times n} \mid \boldsymbol{R} \boldsymbol{R}^{\mathrm{T}}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\} \tag{2-6} SO(n)={R∈Rn×n∣RRT=I,det(R)=1}(2-6)
(4)旋转加平移
可以将三维空间的刚体运动分解为平移以及旋转运动,满足:
a ′ = R a + t (2-7) \boldsymbol{a^{\prime}}=\boldsymbol{Ra+t} \tag{2-7} a′=Ra+t(2-7)
(5)齐次坐标与旋转矩阵(参考机器人学中的坐标变换)
为便于表达,写成齐次形式
[ a ′ 1 ] = [ R t 0 T 1 ] [ a 1 ] = def T [ a 1 ] (2-8) \left[\begin{array}{l} \boldsymbol{a}^{\prime} \\ 1 \end{array}\right]=\left[\begin{array}{ll} \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right]\left[\begin{array}{l} \boldsymbol{a} \\ 1 \end{array}\right] \stackrel{\text { def }}{=} \boldsymbol{T}\left[\begin{array}{l} \boldsymbol{a} \\ 1 \end{array}\right] \tag{2-8} [a′1]=[R0Tt1][a1]= def T[a1](2-8)
其中, T \boldsymbol{T} T即为变换矩阵(注意左乘右乘区别)。
(绕静坐标系(世界坐标系)旋转即左乘,绕自身坐标系旋转即右乘)
这种形式的矩阵集合定义为特殊欧式群,即
S E ( 3 ) = { T = [ R t 0 T 1 ] ∈ R 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } (2-9) \mathrm{SE}(3)=\left\{\boldsymbol{T}=\left[\begin{array}{ll} \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{R} \in \mathrm{SO}(3), \boldsymbol{t} \in \mathbb{R}^{3}\right\} \tag{2-9} SE(3)={T=[R0Tt1]∈R4×4∣R∈SO(3),t∈R3}(2-9)
同样地,逆方向的变换为:
T − 1 = [ R T − R T t 0 T 1 ] (2-10) \boldsymbol{T}^{-1}=\left[\begin{array}{cc} \boldsymbol{R}^{\mathrm{T}} & -\boldsymbol{R}^{\mathrm{T}} \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right] \tag{2-10} T−1=[RT0T−RTt1](2-10)
2.2 旋转向量和欧拉角
2.2.1 旋转向量
(1)三维空间中刚体运动有六个自由度(旋转和平移各三个)。显然无论是上述的旋转矩阵(9个量)还是变换矩阵(16个量),都有很大的冗余;并且,矩阵中的元素相互关联,这不利于后续的非线性优化计算。因此我们希望找到一种更为紧凑的表达方式。
(2)任意一个旋转都可以用旋转轴和旋转角刻画,因此可以用旋转向量(也称为角轴或轴角)来表达,即向量方向为旋转轴,其模长为旋转角。
(3)罗德里格斯公式描述了旋转矩阵和旋转向量之间的关系。
R = cos ( θ I ) + ( 1 − cos θ ) n n T + sin ( θ n ∧ ) (2-11) \boldsymbol{R}=\cos (\theta\boldsymbol{I}) + \left( 1- \cos \theta\right) \boldsymbol{n} {\boldsymbol{n}}^T+\sin (\theta\boldsymbol{n}^{\wedge}) \tag{2-11} R=cos(θI)+(1−cosθ)nnT+sin(θn∧)(2-11)
反之,有
θ = a r c c o s ( t r ( R ) − 1 2 ) (2-12) \theta=arccos(\frac{tr(\boldsymbol{R})-1}{2}) \tag{2-12} θ=arccos(2tr(R)−1)(2-12)
t r ( R ) tr(\boldsymbol{R}) tr(R)表示求迹,即矩阵对角线元素之和。
由于旋转轴在旋转过程中是不动的,则有
R n = n (2-13) \boldsymbol{R}\boldsymbol{n}=\boldsymbol{n} \tag{2-13} Rn=n(2-13)
这说明 n \boldsymbol{n} n是矩阵 R \boldsymbol{R} R特征值为 1 对应的特征向量,由此可以求出向量 n \boldsymbol{n} n的值。
2.2.2 欧拉角
(1)将旋转分解为 X、Y、Z 三个方向上的转动,常用的是 ZYX 顺序的旋转:
- 绕 Z 轴旋转,得到偏航角 yaw;
- 绕旋转后的 Y 轴旋转,得到俯仰角 pitch;
- 绕旋转后的 X 轴旋转,得到滚转角 roll。
此时,使用 [ y , p , r ] T [y, p, r]^T [y,p,r]T这样一个三维向量便可以描述任意旋转。
(2)存在万向锁问题:即当俯仰角为 ±90° 时,第三次旋转轴和第一次旋转轴重合,使系统丢失了一个自由度,这被称为奇异性问题。因此欧拉角在 SLAM 中较少使用。
(3)旋转向量也存在奇异性,当 θ \theta θ超过 2 π 2\pi 2π时会产生周期性,这时将其限定在 2 π 2\pi 2π范围内便可以避免。
2.3 四元数
2.3.1 四元数的定义
(1)2D 情况下,可用单位复数表达旋转,在复数平面中,结合欧拉公式,如下图,向量 z \boldsymbol{z} z旋转 90° ,相当于乘上 i i i。
(2)类似的,在三维空间中,采用四元数描述旋转。四元数有一个实部,三个虚部(分别对应 x、y、z轴)。
q = q 0 + q 1 i + q 2 j + q 3 k (2-14) \boldsymbol{q} = q_0+q_1i+q_2j+q_3k \tag{2-14} q=q0+q1i+q2j+q3k(2-14)
写成向量形式
q = [ s , v ] , s = q 0 ∈ R , v = [ q 1 , q 2 , q 3 ] T ∈ R 3 (2-15) \boldsymbol{q}=[s, \boldsymbol{v}], s=q_0\in \mathbb{R},\boldsymbol{v}=[q_1,q_2,q_3]^T \in \mathbb{R}^3 \tag{2-15} q=[s,v],s=q0∈R,v=[q1,q2,q3]T∈R3(2-15)
并且,虚部之间满足
{ i 2 = j 2 = k 2 = − 1 i j = k , j i = − k j k = i , k j = − i k i = j , i k = − j (2-16) \left\{ \begin{matrix} i^2=j^2=k^2=-1 \\ ij=k, ji=-k \\ jk=i, kj=-i \\ ki=j, ik=-j \end{matrix} \right. \tag{2-16} ⎩ ⎨ ⎧i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j(2-16)
(3)当四元数的实部为 0 时,称为虚四元数(分别对应三维坐标),此时,可以用来表示三维空间中的点。
2.3.2 四元数的计算
-
加法:对应部分相加
-
乘法:每一项相乘,最后相加
-
模长:各项系数平方和再开方;并且两个四元数乘积的模等于各自模的乘积,即 ∣ ∣ q 1 q 2 ∣ ∣ = ∣ ∣ q 1 ∣ ∣ ⋅ ∣ ∣ q 1 ∣ ∣ ||\boldsymbol{q_1}\boldsymbol{q_2}||=||\boldsymbol{q_1}||\cdot||\boldsymbol{q_1}|| ∣∣q1q2∣∣=∣∣q1∣∣⋅∣∣q1∣∣。
-
共轭:实部相等,虚部互为相反数: q a ∗ = [ s a , − v a ] T \boldsymbol{q_a^*}=[s_a, -\boldsymbol{v_a}]^T qa∗=[sa,−va]T。并且, q ∗ q = q q ∗ = [ s 2 + v T v , 0 ] T \boldsymbol{q^*q}=\boldsymbol{qq^*}=[s^2+\boldsymbol{v^Tv}, \boldsymbol{0}]^T q∗q=qq∗=[s2+vTv,0]T
-
逆: q − 1 = q ∗ / ∣ ∣ q ∣ ∣ 2 \boldsymbol{q^{-1}}=\boldsymbol{q^*}/{||\boldsymbol{q}||}^2 q−1=q∗/∣∣q∣∣2,则 q − 1 q = q q − 1 = 1 \boldsymbol{q^{-1}}\boldsymbol{q}=\boldsymbol{q}\boldsymbol{q^{-1}}=1 q−1q=qq−1=1,同时, ( q a q b ) − 1 = q a − 1 q b − 1 (\boldsymbol{q_a}\boldsymbol{q_b})^{-1}=\boldsymbol{q_a}^{-1}\boldsymbol{q_b}^{-1} (qaqb)−1=qa−1qb−1
-
数乘: k q = [ k s , k v ] T k\boldsymbol{q}=[ks, k\boldsymbol{v}]^T kq=[ks,kv]T
2.3.3 四元数表示旋转
(1)三维空间中任意点均可用一个纯虚四元数表示即 p = [ 0 , v ] T \boldsymbol{p}=[0,\boldsymbol{v}]^T p=[0,v]T,经一个单位四元数 q \boldsymbol{q} q的旋转后,得到 p ′ \boldsymbol{p'} p′,则
p ′ = q p q − 1 (2-17) \boldsymbol{p'}=\boldsymbol{q}\boldsymbol{p}\boldsymbol{q^{-1}} \tag{2-17} p′=qpq−1(2-17)
最终 p ′ \boldsymbol{p'} p′的虚部即为旋转后点的坐标。
2.3.4 四元数与其他旋转表示法的转换
- 角轴到四元数:
q = [ c o s θ 2 , n x s i n θ 2 , n y s i n θ 2 , n z s i n θ 2 ] (2-18) \boldsymbol{q}=[cos{\frac{\theta}{2}},n_xsin{\frac{\theta}{2}}, n_ysin{\frac{\theta}{2}},n_zsin{\frac{\theta}{2}}] \tag{2-18} q=[cos2θ,nxsin2θ,nysin2θ,nzsin2θ](2-18)
-
四元数到角轴
{ θ = 2 a r c c o s q 0 [ n x , n y , n z ] T = [ q 1 , q 2 , q 3 ] T / s i n θ 2 (2-19) \left\{ \begin{matrix} \theta=2arccos{q_0} \\ \\ [n_x, n_y, n_z]^T=[q_1, q_2, q_3]^T/sin{\frac{\theta}{2}} \end{matrix} \right. \tag{2-19} ⎩ ⎨ ⎧θ=2arccosq0[nx,ny,nz]T=[q1,q2,q3]T/sin2θ(2-19) -
四元数到旋转矩阵
-
旋转矩阵到四元数
2.4 相似、仿射、射影变换
欧式变换不改变向量本身,只是进行旋转或平移。
(1)相似变换
相似变换比欧式变换多了一个自由度,即相当于在旋转或平移后,各坐标再进行等比例缩放,表达式为
T s = [ s R t 0 T 1 ] (2-20) \boldsymbol{T}_s=\left[\begin{array}{ll} s\boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right] \tag{2-20} Ts=[sR0Tt1](2-20)
s s s为缩放因子。
(2)仿射变换
表达式如下:
T A = [ A t 0 T 1 ] (2-21) \boldsymbol{T}_A=\left[\begin{array}{ll} \boldsymbol{A} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right] \tag{2-21} TA=[A0Tt1](2-21)
这里不要求 A \boldsymbol{A} A为正交矩阵,因此,变换后,正方形就不是方的了,但仍是平行四边形。
(3)射影变换
T P = [ A t a T v ] (2-22) \boldsymbol{T}_P=\left[\begin{array}{ll} \boldsymbol{A} & \boldsymbol{t} \\ \mathbf{a}^{\mathrm{T}} & v \end{array}\right] \tag{2-22} TP=[AaTtv](2-22)
射影变换是最一般的变换,左上角 A \boldsymbol{A} A为可逆矩阵,右上角 t \boldsymbol{t} t为平移,左下角为缩放 a T \boldsymbol{a^T} aT。从真实世界到相机照片的变换可以看做是射影变换:原本正方形的地砖,在照片中将不再是方形,由于近大远小,甚至可能是不规则的四边形。
相关文章:

《视觉SLAM十四讲》-- 三维空间的刚体运动
文章目录 02 三维空间的刚体运动2.0 机器人位姿表述2.1 点和坐标系2.1.1 三维坐标系有关表述2.1.2 坐标系变换 2.2 旋转向量和欧拉角2.2.1 旋转向量2.2.2 欧拉角 2.3 四元数2.3.1 四元数的定义2.3.2 四元数的计算2.3.3 四元数表示旋转2.3.4 四元数与其他旋转表示法的转换 2.4 相…...

关于iOS:如何使用SwiftUI调整图片大小?
How to resize Image with SwiftUI? 我在Assets.xcassets中拥有很大的形象。 如何使用SwiftUI调整图像大小以缩小图像? 我试图设置框架,但不起作用: 1 2 Image(room.thumbnailImage) .frame(width: 32.0, height: 32.0) 在Image上应用…...

【MySQL】数据库MySQL基础知识与操作
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《MySQL》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&a…...
)
vim手册(vim cheatsheet)
vim手册(vim cheatsheet) 1. 命令模式 1). 移动光标 在命令模式下,可以使用以下命令来移动光标: - h:向左移动一个字符。 - j:向下移动一行。 - k:向上移动一行。 - l:向右移动一个…...
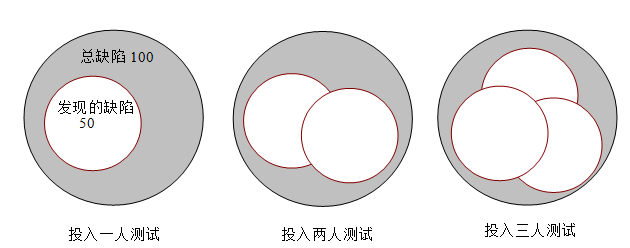
软件测试具体人员分工
最近看了点敏捷测试的东西,看得比较模糊。一方面是因为没有见真实的环境与流程,也许它跟本就没有固定的模式与流程,它就像告诉人们要“勇敢”“努力”。有的人在勇敢的面对生活,有些人在勇敢的挑战自我,有些人在勇敢的…...
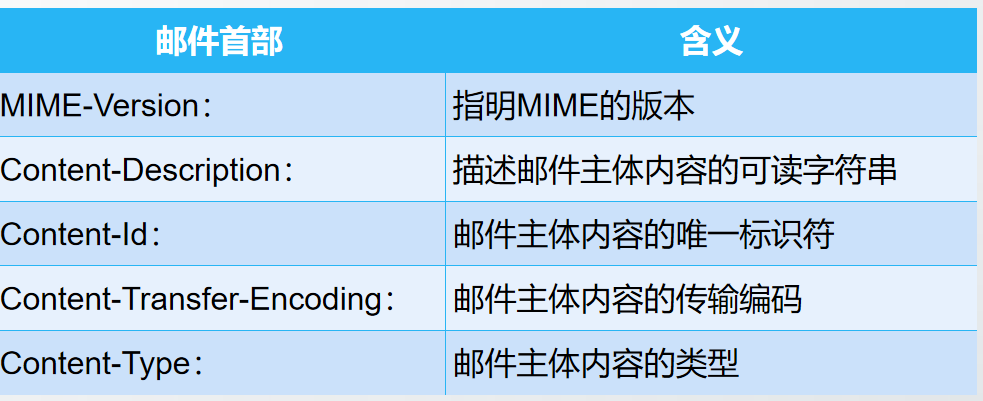
计算机网络-应用层
文章目录 应用层协议原理万维网和HTTP协议万维网概述统一资源定位符HTML文档 超文本传输协议(HTTP)HTTP报文格式请求报文响应报文cookie 万维网缓存与代理服务器 DNS系统域名空间域名服务器和资源记录域名解析过程递归查询迭代查询 动态主机配置协议&…...
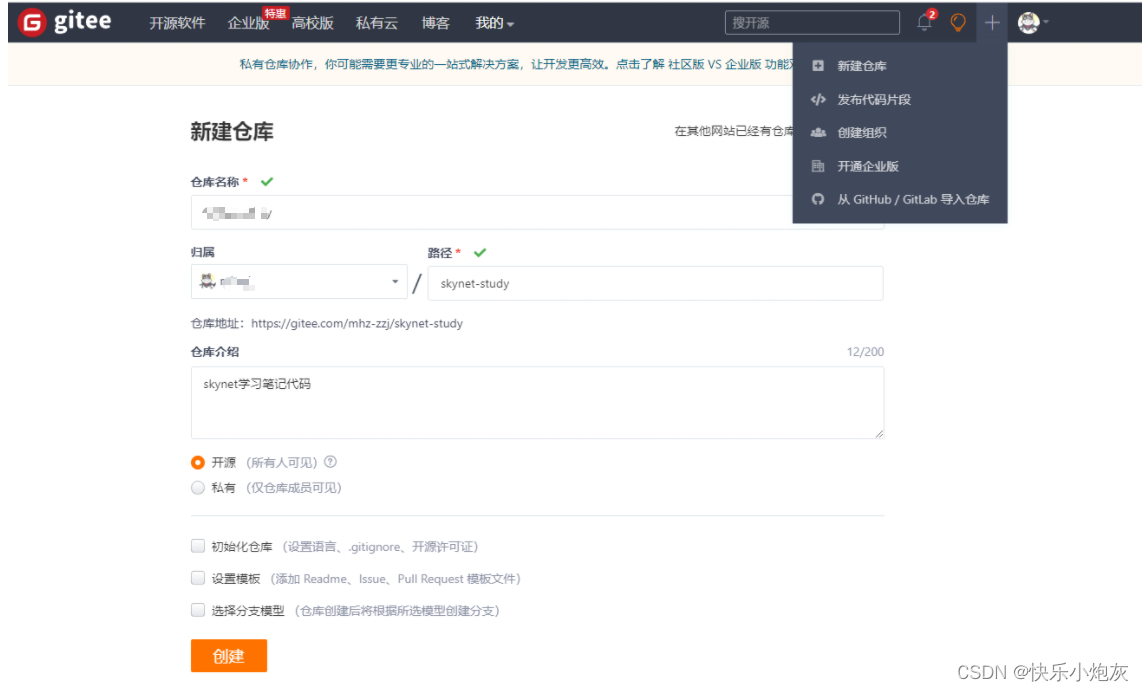
linux 创建git项目并提交到gitee(保姆式教程)
01、git安装与初始化设置 mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ apt install mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ git config --global user.name "用户名" mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ git config --global user.ema…...

STM32 IAP应用开发--bootloader升级程序
STM32 IAP应用开发--bootloader升级程序 Chapter1 STM32 IAP应用开发——通过串口/RS485实现固件升级(方式2)前言什么是IAP?什么是BootLoader? 方案介绍:1)bootloader部分:2)APP部分…...

Q_GLOBAL_STATIC宏
文章目录 目的Q_GLOBAL_STATIC源代码分析涉及到原子操作 以及静态变量初始化顺序代码实现 目的 由Q_GLOBAL_STATIC宏, 引发的基于线程安全的Qt 单例模式的使用。 Q_GLOBAL_STATIC /***************************************************************************…...

[批处理]_[初级]_[如何删除变量值里的双引号]
场景 在使用Visual Studio开发本地程序的时,需要在项目属性,生成事件->生成后事件里增加一些资源的打包,复制,删除等操作,那么就需要用到批处理来进行。而传递带空格的路径给外部的批处理文件时就需要双引号引用从…...
51单片机电子钟闹钟温度LCD1602液晶显示设计( proteus仿真+程序+原理图+设计报告+讲解视频)
51单片机电子钟闹钟温度液晶显示设计( proteus仿真程序原理图设计报告讲解视频) 1.主要功能:2.仿真3. 程序代码4. 原理图5. 设计报告6. 设计资料内容清单&&下载链接资料下载链接(可点击): 🌟51单片…...

怎样学好java
最近在看一本java方面的书。《java从入门到精通》,里面看到一段如何学习java的话,觉得非常好,下面我分享一下。 如何学好java语言,是所有初学者都需要面对的问题。其实,每种语言的学习方法都大同小异。初学者需要注意…...

HarmonyOS 数据管理与应用数据持久化(二)
通过键值型数据库实现数据持久化 场景介绍 键值型数据库存储键值对形式的数据,当需要存储的数据没有复杂的关系模型,比如存储商品名称及对应价格、员工工号及今日是否已出勤等,由于数据复杂度低,更容易兼容不同数据库版本和设备…...
Hadoop环境搭建及Demo
参考博客 Windows 10安装Hadoop 3.3.0教程 (kontext.tech) Hadoop入门篇——伪分布模式安装 & WordCount词频统计 | Liu Baoshuai’s Blog Hadoop安装教程 Linux版_linux和hadoop的安装_lnlnldczxy的博客-CSDN博客 hadoop启动出错 The value of property bind.address …...
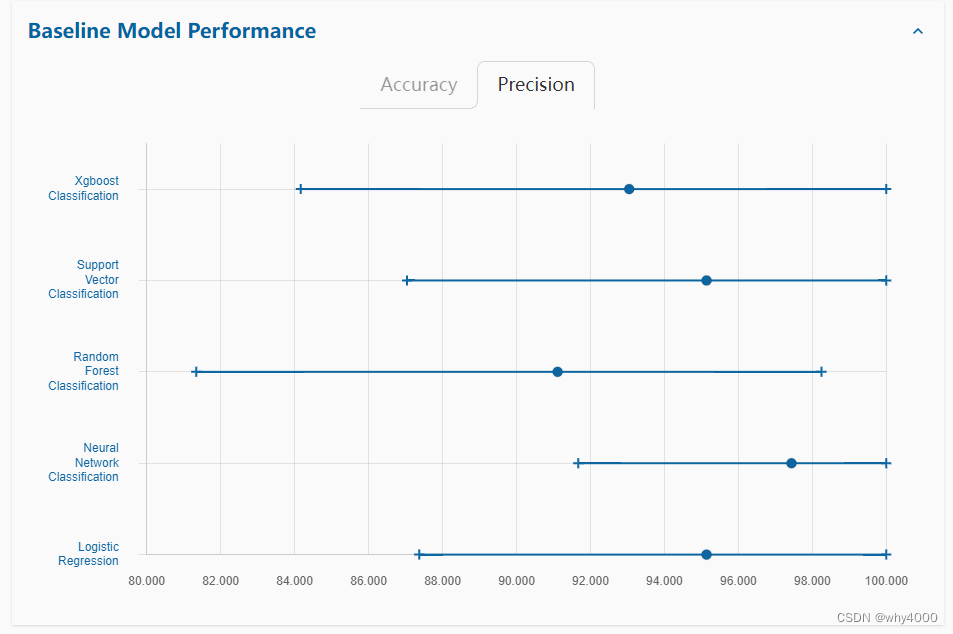
更新一下数据集
UCI Machine Learning Repository UCI的数据集还是挺老牌的,最近换了地址,我就再记录一下。 左边是比较常见的数据集,比如Iris很经典,Heart Disease这也是,包括Wine,通常对于初学者学习比较好,…...

web3之跨链预言机SupraOracles:什么是Supra
文章目录 web3之跨链预言机SupraOracles什么是Supra什么是DORA(分布式Oracle协议)使用场景web3之跨链预言机SupraOracles 什么是Supra 官网:https://supraoracles.com/ 预言机的核心价值就在于数据传输,数据传输的速度、准确性、安全性更是重中之重。Supra Oracles 就是这…...

关系型数据库 期末复习(未完
关系型数据库 绪论概念间的关系数据库的历史信息和数据数据模型 关系模型数据结构关系完整性关系操作语言 关系代数语言 绪论 概念间的关系 数据->数据库->数据库管理系统->数据库系统 数据库的历史 人工管理阶段 -> 文件系统阶段 -> 数据库系统阶段 数据库…...

【学习笔记】CF1895G Two Characters, Two Colors
感谢grass8sheep提供的思路。 首先,我们可以用 D P DP DP解决这个问题。 设 f i , j f_{i,j} fi,j表示前 i i i个数中有 j j j个为 1 1 1的位置为红色的最大价值。则转移如下: f i , j ← f i − 1 , j b i f_{i,j}\gets f_{i-1,j}b_i fi,j←fi−…...
GZ035 5G组网与运维赛题第10套
2023年全国职业院校技能大赛 GZ035 5G组网与运维赛项(高职组) 赛题第10套 一、竞赛须知 1.竞赛内容分布 竞赛模块1--5G公共网络规划部署与开通(35分) 子任务1:5G公共网络部署与调试(15分) 子…...

基于SSM的教学管理系统(有报告)。Javaee项目。
演示视频: 基于SSM的教学管理系统(有报告)。Javaee项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构,通过Spring SpringMvc My…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
