RIP路由配置
RIP路由配置步骤与命令:
1.启用RIP路由:router rip
2.通告直连网络:network 直连网络
3.启用RIPv2版本:version 2
4.禁用自动汇总:no auto-summary
注意:静态路由通告远程网络,动态路由通告直连网络。
配置实例:
如下图,通过配置RIP动态路由使得网络畅通,使得PC001能与PC002通信。
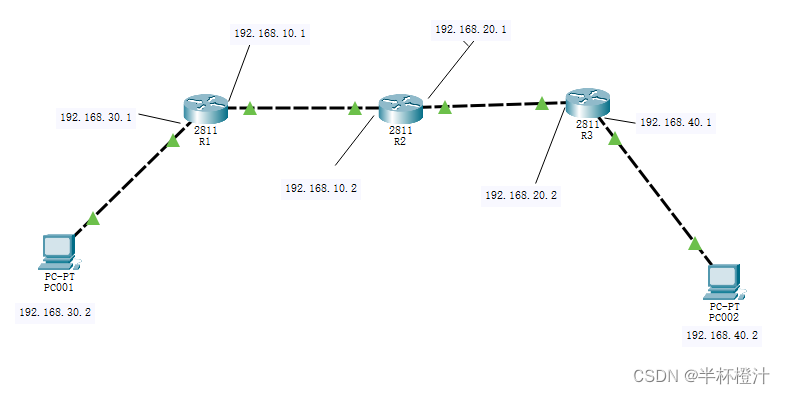
配置步骤:
一、在R1路由器上启用RIP并通告直连网络。
R1(config)#router rip
R1(config-router)#network 192.168.30.0
R1(config-router)#network 192.168.10.0
R1(config-router)#version 2
R1(config-router)#no auto-summary
二、在R2路由器上启用RIP并通告直连网络。
R2(config)#router rip
R2(config-router)#network 192.168.10.0
R2(config-router)#network 192.168.20.0
R2(config-router)#version 2
R2(config-router)#no auto-summary
三、在R3路由器上启用RIP并通告直连网络。
R3(config)#router rip
R3(config-router)#network 192.168.20.0
R3(config-router)#network 192.168.40.0
R3(config-router)#version 2
R3(config-router)#no auto-summary
验证:
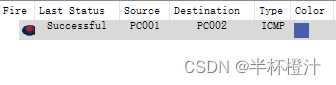
相关文章:

RIP路由配置
RIP路由配置步骤与命令: 1.启用RIP路由:router rip 2.通告直连网络:network 直连网络 3.启用RIPv2版本:version 2 4.禁用自动汇总:no auto-summary 注意:静态路由通告远程网络,动态路由通告…...
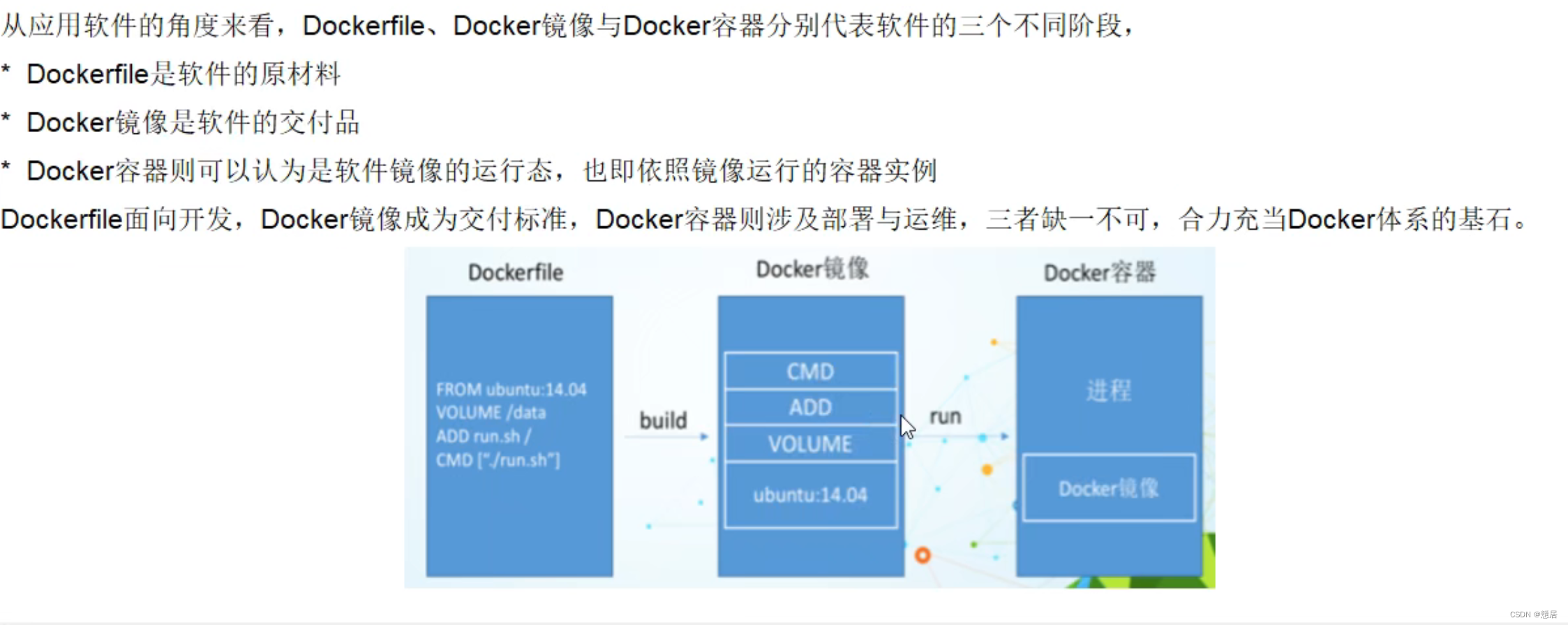
尚硅谷Docker基础篇和Dockerfile超详细整合笔记
Docker基础篇DockerFile Docker:您要如何确保应用能够在这些环境中运行和通过质量检测?并且在部署过程中不出现令人头疼的版本、配置问题,也无需重新编写代码和进行故障修复?而这个就是使用容器。Docker解决了运行环境和配置问题…...
JavaScript_Date对象_实例方法_get类
计算这一年还剩多少天: <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>Document&…...

Go语言在区块链开发中的应用
引言 区块链是近年来备受关注的技术领域,它不仅改变了传统的数据交换和存储方式,还为各种应用场景提供了全新的解决方案。而Go语言(Golang)作为一门简洁、高效的编程语言,正逐渐成为开发区块链应用的首选语言。本文将…...

S4.2.4.5 Fast Training Sequence (FTS)
一 本章节主讲知识点 1.1 FTS的用途和实现注意 二 本章节原文翻译 Fast Training Sequence (FTS) 主要用于在L0s->L0跳转的过程中,让Receiver 检测到电气空闲退出,以及实现bit 和 symbol lock。 2.1 Gen1 and Gen2 速率 对于Gen1/2 FTS的组成如下…...

Gitlab CICD实用技巧汇总
关于.gitlab-ci.yml的实用配置 1、stage参数 stages: - build - test - deploy 相同stage的作业会并行执行,有一个失败,则认为这个stage失败。 不同stage的作业会按序执行,前面stage有失败,后续stage不会继续执行。 可以使用ne…...
JavaSpringbootMySQL高校实训管理平台01557-计算机毕业设计项目选题推荐(附源码)
目 录 摘要 1 绪论 1.1 研究背景 1.2 研究意义 1.3论文结构与章节安排 2 高校实训管理平台系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1 数据增加流程 2.2.2 数据修改流程 2.2.3 数据删除流程 2.3 系统功能分析 2.3.1 功能性分析 2.3.2 非功能性分析 2.4 系…...

初阶JavaEE(14)表白墙程序
接上次博客:初阶JavaEE(13)(安装、配置:Smart Tomcat;访问出错怎么办?Servlet初识、调试、运行;HttpServlet:HttpServlet;HttpServletResponse)-C…...
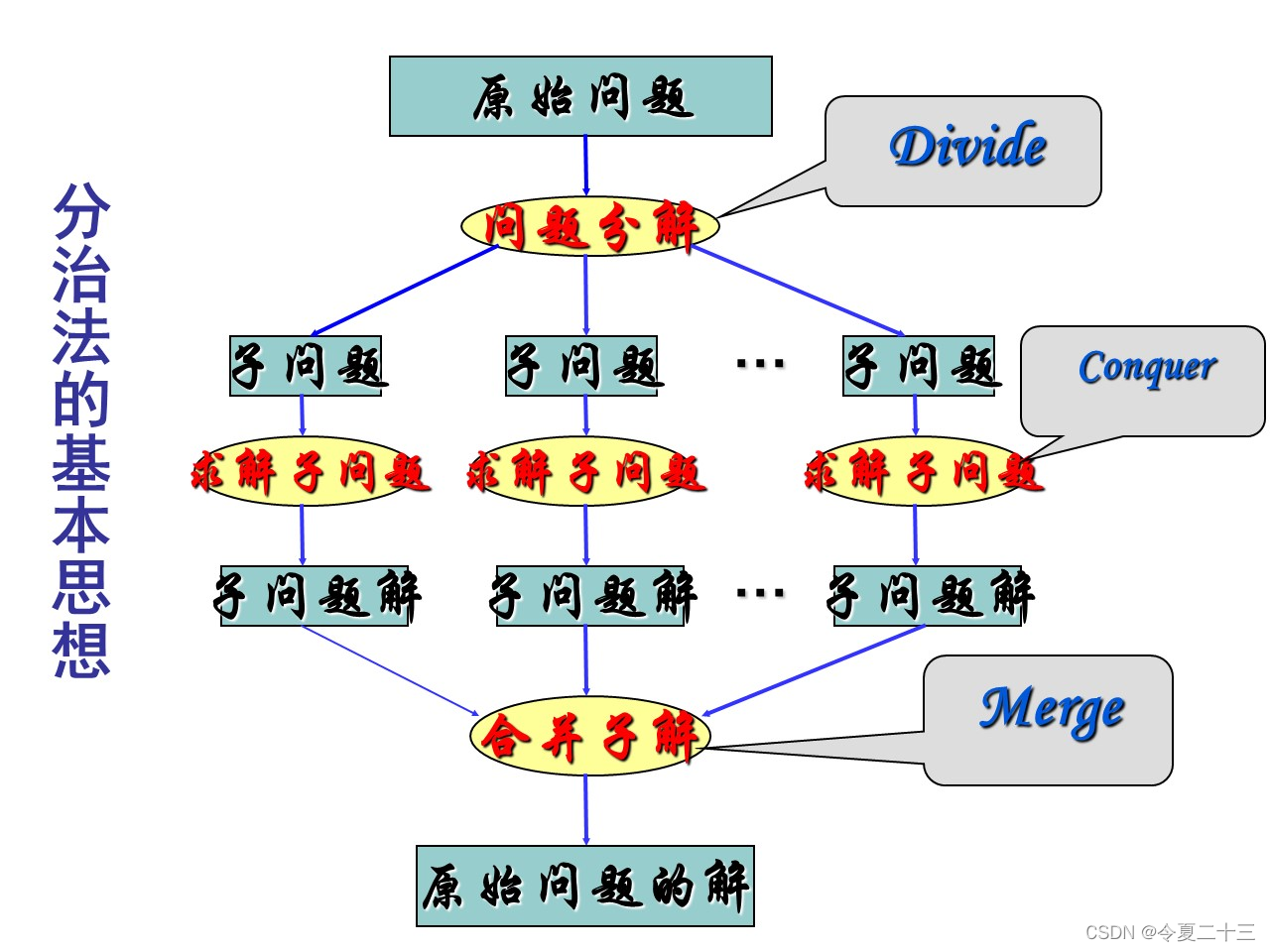
算法设计与分析第二章作业
1. 描述最大字段和的分治算法 题目 思路 判断最大子段和,可以用分治的思想,每次将序列一分为二,选择两个序列的最大子段和。 但是这里还有一种可能,就是子段可以横跨两个子序列,所以我们的最大子段和就是࿱…...

《视觉SLAM十四讲》-- 三维空间的刚体运动
文章目录 02 三维空间的刚体运动2.0 机器人位姿表述2.1 点和坐标系2.1.1 三维坐标系有关表述2.1.2 坐标系变换 2.2 旋转向量和欧拉角2.2.1 旋转向量2.2.2 欧拉角 2.3 四元数2.3.1 四元数的定义2.3.2 四元数的计算2.3.3 四元数表示旋转2.3.4 四元数与其他旋转表示法的转换 2.4 相…...

关于iOS:如何使用SwiftUI调整图片大小?
How to resize Image with SwiftUI? 我在Assets.xcassets中拥有很大的形象。 如何使用SwiftUI调整图像大小以缩小图像? 我试图设置框架,但不起作用: 1 2 Image(room.thumbnailImage) .frame(width: 32.0, height: 32.0) 在Image上应用…...

【MySQL】数据库MySQL基础知识与操作
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《MySQL》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&a…...
)
vim手册(vim cheatsheet)
vim手册(vim cheatsheet) 1. 命令模式 1). 移动光标 在命令模式下,可以使用以下命令来移动光标: - h:向左移动一个字符。 - j:向下移动一行。 - k:向上移动一行。 - l:向右移动一个…...
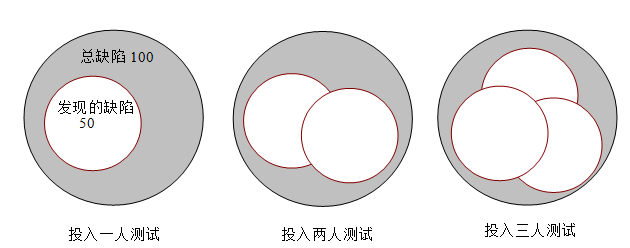
软件测试具体人员分工
最近看了点敏捷测试的东西,看得比较模糊。一方面是因为没有见真实的环境与流程,也许它跟本就没有固定的模式与流程,它就像告诉人们要“勇敢”“努力”。有的人在勇敢的面对生活,有些人在勇敢的挑战自我,有些人在勇敢的…...
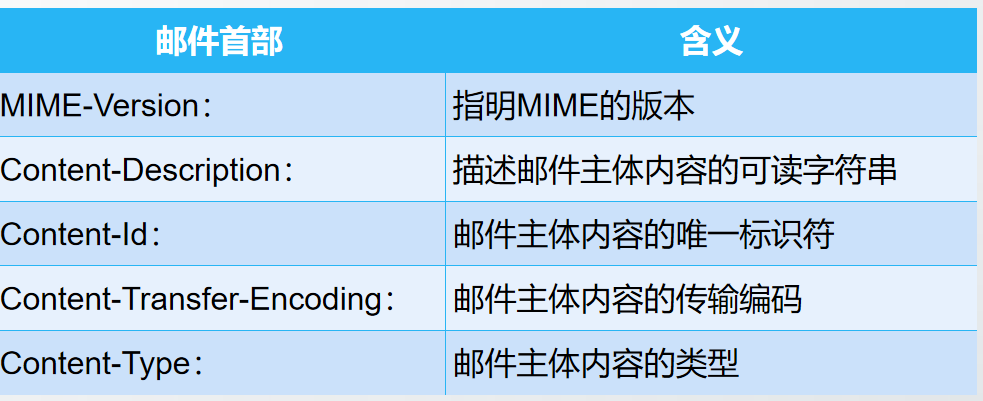
计算机网络-应用层
文章目录 应用层协议原理万维网和HTTP协议万维网概述统一资源定位符HTML文档 超文本传输协议(HTTP)HTTP报文格式请求报文响应报文cookie 万维网缓存与代理服务器 DNS系统域名空间域名服务器和资源记录域名解析过程递归查询迭代查询 动态主机配置协议&…...
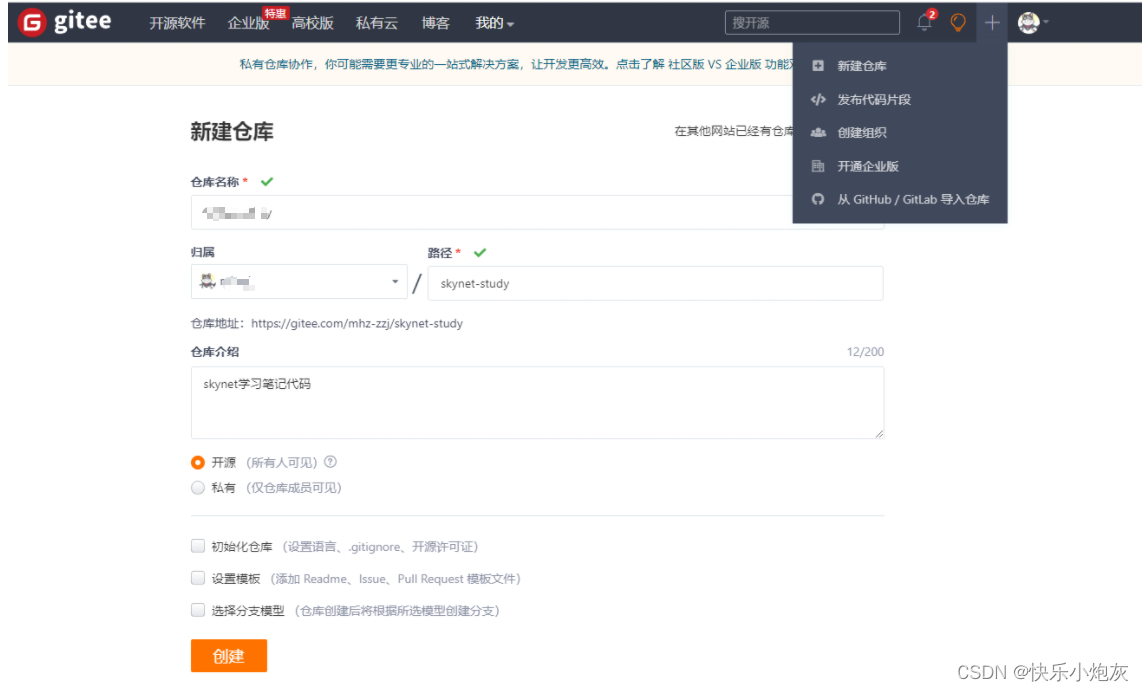
linux 创建git项目并提交到gitee(保姆式教程)
01、git安装与初始化设置 mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ apt install mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ git config --global user.name "用户名" mhzzjmhzzj-virtual-machine:~/work/skynetStudy$ git config --global user.ema…...

STM32 IAP应用开发--bootloader升级程序
STM32 IAP应用开发--bootloader升级程序 Chapter1 STM32 IAP应用开发——通过串口/RS485实现固件升级(方式2)前言什么是IAP?什么是BootLoader? 方案介绍:1)bootloader部分:2)APP部分…...

Q_GLOBAL_STATIC宏
文章目录 目的Q_GLOBAL_STATIC源代码分析涉及到原子操作 以及静态变量初始化顺序代码实现 目的 由Q_GLOBAL_STATIC宏, 引发的基于线程安全的Qt 单例模式的使用。 Q_GLOBAL_STATIC /***************************************************************************…...

[批处理]_[初级]_[如何删除变量值里的双引号]
场景 在使用Visual Studio开发本地程序的时,需要在项目属性,生成事件->生成后事件里增加一些资源的打包,复制,删除等操作,那么就需要用到批处理来进行。而传递带空格的路径给外部的批处理文件时就需要双引号引用从…...
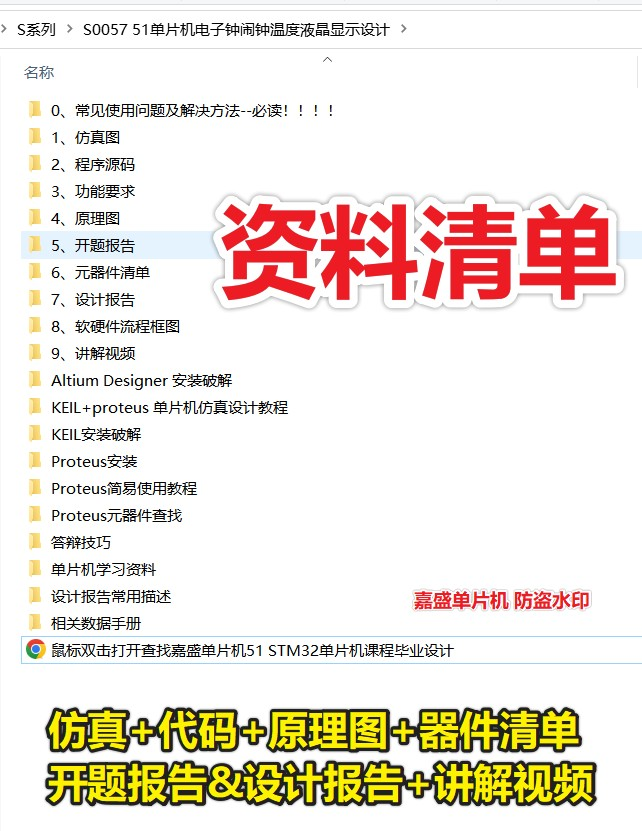
51单片机电子钟闹钟温度LCD1602液晶显示设计( proteus仿真+程序+原理图+设计报告+讲解视频)
51单片机电子钟闹钟温度液晶显示设计( proteus仿真程序原理图设计报告讲解视频) 1.主要功能:2.仿真3. 程序代码4. 原理图5. 设计报告6. 设计资料内容清单&&下载链接资料下载链接(可点击): 🌟51单片…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
