当前位置： 首页 > news >正文

connect-history-api-fallback原理

news 2025/11/8 17:49:45

connect-history-api-fallback是一个用于处理前端路由的中间件，它的原理是在服务器接收到请求时，检查请求的路径是否匹配到静态文件（如HTML、CSS、JS等），如果不匹配，则将请求重定向到前端的入口文件，通常是 index.html。这样做的目的是确保在使用前端路由时，刷新页面或直接访问某个路由时，服务器都能正确地返回前端入口文件，并由前端路由来处理路由匹配和页面渲染。

具体工作原理如下：

当服务器接收到一个请求时，connect-history-api-fallback中间件会检查该请求的路径是否匹配到静态文件。
如果路径匹配到静态文件，服务器会返回该静态文件的内容，如常规的文件请求处理流程。
如果路径不匹配到静态文件，服务器会将请求重定向到前端的入口文件，通常是 index.html。
前端的入口文件会被加载并执行，然后前端路由根据请求的路径进行路由匹配和页面渲染。
通过使用 connect-history-api-fallback 中间件，服务器可以正确地处理前端路由的历史模式，确保在刷新页面或直接访问某个路由时返回正确的内容，而不是返回404错误。这样就能够保证前端路由在各种情况下的正常工作。

需要注意的是，不同的服务器可能有不同的配置方式来使用 connect-history-api-fallback，例如在Express服务器中使用 app.use(history()) 进行中间件的注册。具体的配置方式请参考相关服务器和中间件的文档。

相关文章：

connect-history-api-fallback原理

connect-history-api-fallback是一个用于处理前端路由的中间件，它的原理是在服务器接收到请求时，检查请求的路径是否匹配到静态文件（如HTML、CSS、JS等），如果不匹配，则将请求重定向到前端的入口文件&#x…...

编程日记 2023/11/6 0:23:17

Android ConstraintLayout分组堆叠圆角ShapeableImageView

Android ConstraintLayout分组堆叠圆角ShapeableImageView <?xml version"1.0" encoding"utf-8"?> <androidx.constraintlayout.widget.ConstraintLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"…...

编程日记 2023/11/6 0:22:16

Docker Stack部署应用详解+Tomcat项目部署详细实战

Docker Stack 部署应用 概述 单机模式下&#xff0c;可以使用 Docker Compose 来编排多个服务。Docker Swarm 只能实现对单个服务的简单部署。而Docker Stack 只需对已有的 docker-compose.yml 配置文件稍加改造就可以完成 Docker 集群环境下的多服务编排。 stack是一组共享…...

编程日记 2023/11/6 0:21:14

Compose-Multiplatform在Android和iOS上的实践

本文字数&#xff1a;4680字 预计阅读时间&#xff1a;30分钟 01 简介 之前我们探讨过KMM&#xff0c;即Kotlin Multiplatform Mobile&#xff0c;是Kotlin发布的移动端跨平台框架。当时的结论是KMM提倡将共有的逻辑部分抽出&#xff0c;由KMM封装成Android(Kotlin/JVM)的aar和…...

编程日记 2023/11/6 0:20:14

XXL-JOB 默认 accessToken 身份绕过导致 RCE

文章目录 0x01 漏洞介绍0x02 影响版本0x03 环境搭建0x04 漏洞复现第一步 访问页面返回报错信息第二步 执行POC,进行反弹shell第三步 获取shell0x05 修复建议摘抄免责声明0x01 漏洞介绍 XXL-JOB 是一款开源的分布式任务调度平台，用于实现大规模任务的调度和执行。 XXL-JOB 默…...

编程日记 2023/11/6 0:19:13

7 库函数之复位和时钟设置（RCC）所有函数的介绍及使用

7 库函数之复位和时钟设置（RCC）所有函数的介绍及使用的介绍及使用 1. 图片有格式二、RCC库函数固件库函数预览2.1 函数RCC_DeInit2.2 函数RCC_HSEConfig2.3 函数RCC_WaitForHSEStartUp2.4 函数RCC_AdjustHSICalibrationValue2.5 函数RCC_HSICmd2.6 函数RCC_PLLConfig2.7 函数…...

编程日记 2023/11/6 0:18:11

第十七节——指令

一、概念 在Vue.js中&#xff0c;指令&#xff08;Directives&#xff09;是一种特殊的语法&#xff0c;用于为HTML元素添加特定的行为和功能。指令以v-作为前缀&#xff0c;通过在HTML标签中使用这些指令来操作DOM&#xff0c;修改元素的属性、样式或行为。 Vue.js提供了一组…...

编程日记 2023/11/6 0:16:09

优雅的 Dockerfile 是怎样炼成的？

Docker 简介 目前&#xff0c;Docker 主要有两个形态&#xff1a;Docker Desktop 和 Docker Engine。 Docker Desktop 是专门针对个人使用而设计的&#xff0c;支持 Mac&#xff08;已支持arm架构的M系芯片&#xff09; 和 Windows 快速安装&#xff0c;具有直观的图形界面&a…...

编程日记 2023/11/6 0:15:07

2023-2024 中国科学引文数据库来源期刊列表（CSCD）

文章目录 CSCD来源期刊遴选报告2023-2024 中国科学引文数据库来源期刊列表&#xff08;CSCD&#xff09; CSCD来源期刊遴选报告 2023-2024 中国科学引文数据库来源期刊列表&#xff08;CSCD&#xff09;...

编程日记 2023/11/6 0:14:06

【3D图像分割】基于Pytorch的VNet 3D图像分割5（改写数据流篇）

在这篇文章&#xff1a;【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割2&#xff08;基础数据流篇&#xff09; 的最后&#xff0c;我们提到了&#xff1a; 在采用vent模型进行3d数据的分割训练任务中&#xff0c;输入大小是16*96*96&#xff0c;这个的裁剪是放到Dataset类…...

编程日记 2023/11/6 0:13:05

WebSocket Day02 : 握手连接

前言 握手连接是WebSocket建立通信的第一步&#xff0c;通过客户端和服务器之间的一系列握手操作&#xff0c;确保了双方都支持WebSocket协议&#xff0c;并达成一致的通信参数。握手连接的过程包括客户端发起握手请求、服务器响应握手请求以及双方完成握手连接。完成握手连接后…...

编程日记 2023/11/6 0:12:03

c#的反编译工具ISPY和net reflector 使用比较

我有一份Asp.net程序需要修改&#xff0c;但没有源码&#xff0c;只有dll&#xff0c;需要使用反编译工具回复源码&#xff0c;尝试使用了市面上的两种主流的工具ISPY和net reflector &#xff0c;最终用ISPY恢复了源码。 比较 ISPY 恢复的代码和实际有差距&#xff0c;但还能…...

编程日记 2023/11/6 0:11:02

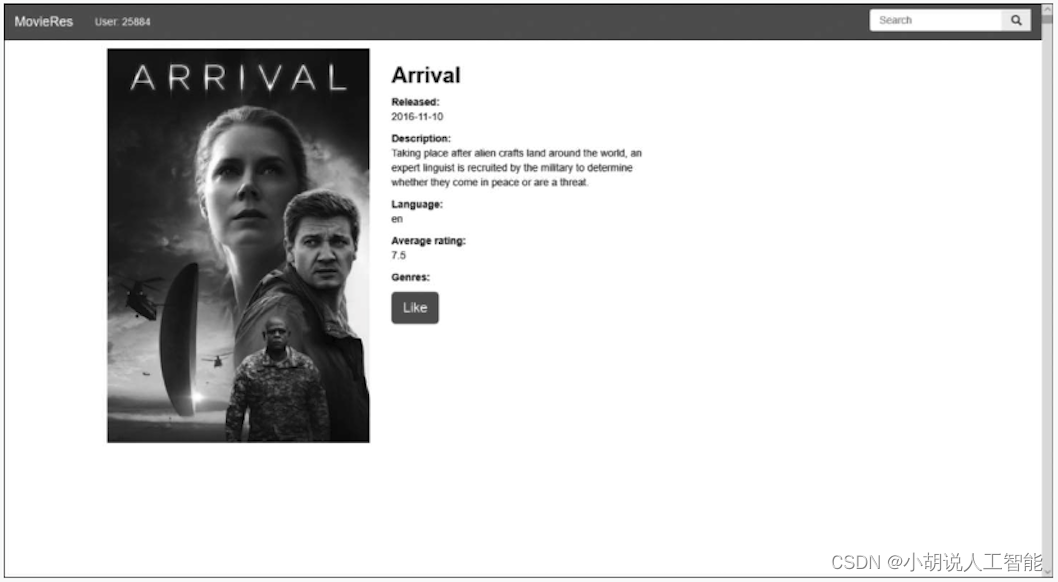
基于LDA主题+协同过滤+矩阵分解算法的智能电影推荐系统——机器学习算法应用(含python、JavaScript工程源码)+MovieLens数据集（四）

目录 前言总体设计系统整体结构图系统流程图 运行环境模块实现1. 数据爬取及处理2. 模型训练及保存3. 接口实现4. 收集数据5. 界面设计 系统测试相关其它博客工程源代码下载其它资料下载 前言 前段时间&#xff0c;博主分享过关于一篇使用协同过滤算法进行智能电影推荐系统的博…...

编程日记 2023/11/6 0:09:00

方阵行列式与转置矩阵

1.转置矩阵&#xff1a;格式规定&#xff1a;如果矩阵A为n阶方阵&#xff0c;那么A的T次方为矩阵A的转置矩阵&#xff0c;即将矩阵A的行与列互换。 2.转置矩阵的运算性质&#xff1a; 1.任何方阵的转置矩阵的转置矩阵为方阵自身。 2.多个矩阵的和的转置矩阵等于多个转置矩阵的…...

编程日记 2023/11/6 0:07:58

【Java 进阶篇】Java Cookie共享：让数据穿越不同应用的时空隧道

在Web开发中&#xff0c;Cookie是一种常见的会话管理技术&#xff0c;用于存储和传递用户相关的信息。通常&#xff0c;每个Web应用都会在用户的浏览器中设置自己的Cookie&#xff0c;以便在用户与应用之间保持状态。然而&#xff0c;有时我们需要在不同的应用之间共享Cookie数…...

编程日记 2023/11/6 0:06:56

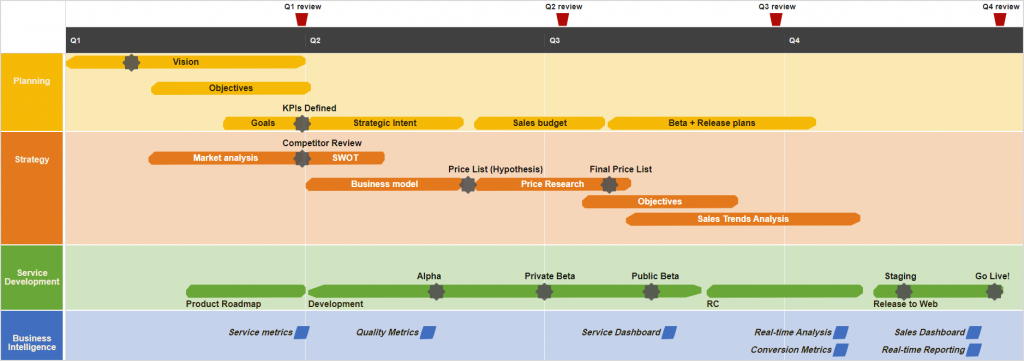
甘特图组件DHTMLX Gantt用例 - 如何拆分任务和里程碑项目路线图

创建一致且引人注意的视觉样式是任何项目管理应用程序的重要要求&#xff0c;这就是为什么我们会在这个系列中继续探索DHTMLX Gantt图库的自定义。在本文中我们将考虑一个新的甘特图定制场景&#xff0c;DHTMLX Gantt组件如何创建一个项目路线图。 DHTMLX Gantt正式版下载 用…...

编程日记 2023/11/6 0:05:55

克里金插值matlab代码

% 克里金插值示例 clc; clear; % 生成模拟数据 x linspace(0, 10, 11); y linspace(0, 10, 11); [X, Y] meshgrid(x, y); Z sin(sqrt(X.^2 Y.^2)) 0.1 * randn(size(X)); % 设置克里金参数 nugget 0.1; % 块金值 range 1; % 范围 sill 1; % 基台值 azimuth …...

编程日记 2023/11/6 0:04:54

【LeetCode】23. 合并 K 个升序链表

题目链接&#xff1a;23. 合并 K 个升序链表 题目描述&#xff1a; 数据范围&#xff1a; **思考&#xff1a;**这题实际上就是合并两个有序列表的进阶版&#xff0c;只不过这里变成了合并K个&#xff0c;那么这里我们显然就知道&#xff0c;核心的合并两个有序列表的思路不…...

编程日记 2023/11/6 0:03:53

2023年【熔化焊接与热切割】免费试题及熔化焊接与热切割考试总结

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 熔化焊接与热切割免费试题参考答案及熔化焊接与热切割考试试题解析是安全生产模拟考试一点通题库老师及熔化焊接与热切割操作证已考过的学员汇总&#xff0c;相对有效帮助熔化焊接与热切割考试总结学员顺利通过考试。…...

编程日记 2023/11/6 0:02:52

为什么要学中文编程？它能有哪些益处？免费版编程工具怎么下载？系统化的编程教程课程怎么学习

一、为什么要学习这个编程工具&#xff1f;能给自己带来什么益处&#xff1f; 1、不论在哪里上班&#xff0c;都不是铁饭碗&#xff1a;现在全球经济低迷&#xff0c;使得很多企业倒闭&#xff0c; 大到知名国企小到私营企业&#xff0c;大量裁员。任何人都无法保证自己现在的…...

编程日记 2023/11/6 0:01:51

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2025/11/7 14:02:25

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2025/7/5 11:03:11

Oracle查询表空间大小

1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

编程新知 2025/11/8 0:24:13

测试markdown--肇兴

day1&#xff1a; 1、去程&#xff1a;7:04 --11:32高铁 高铁右转上售票大厅2楼&#xff0c;穿过候车厅下一楼&#xff0c;上大巴车 &#xffe5;10/人 **2、到达&#xff1a;**12点多到达寨子&#xff0c;买门票&#xff0c;美团/抖音&#xff1a;&#xffe5;78人 3、中饭&a…...

编程新知 2025/10/19 8:14:08

微信小程序 - 手机震动

一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注&#xff1a;文档 https://developers.weixin.qq…...

编程新知 2025/11/8 4:39:49

vue3 定时器-定义全局方法 vue+ts

1.创建ts文件 路径&#xff1a;src/utils/timer.ts 完整代码&#xff1a; import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

编程新知 2025/8/9 0:31:20

云原生安全实战：API网关Kong的鉴权与限流详解

&#x1f525;「炎码工坊」技术弹药已装填&#xff01; 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关&#xff08;API Gateway&#xff09; API网关是微服务架构中的核心组件&#xff0c;负责统一管理所有API的流量入口。它像一座…...

编程新知 2025/11/8 5:25:23

接口自动化测试：HttpRunner基础

相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具&#xff0c;支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议&#xff0c;涵盖接口测试、性能测试、数字体验监测等测试类型…...

编程新知 2025/11/8 6:45:44

【LeetCode】3309. 连接二进制表示可形成的最大数值（递归|回溯|位运算）

LeetCode 3309. 连接二进制表示可形成的最大数值&#xff08;中等&#xff09; 题目描述解题思路Java代码 题目描述 题目链接&#xff1a;LeetCode 3309. 连接二进制表示可形成的最大数值&#xff08;中等&#xff09; 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

编程新知 2025/7/5 18:01:05

node.js的初步学习

那什么是node.js呢&#xff1f; 和JavaScript又是什么关系呢&#xff1f; node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说&#xff0c; 需要在node.js的环境上进行当JavaScript作为前端开发语言来说&#xff0c;需要在浏览器的环境上进行 Node.js 可…...

编程新知 2025/10/20 6:50:54