【位运算】XOR Construction—CF1895D
XOR Construction—CF1895D
参考文章
翻译
题目要求构造一个长度为 n n n 的数组 b b b,满足以下条件:
- 数组 b b b 中包含从 0 0 0 到 n − 1 n-1 n−1 的每个整数,且每个整数仅出现一次;
- 对于 i i i 从 1 1 1 到 n − 1 n-1 n−1, b i ⊕ b i + 1 = a i b_i \oplus b_{i+1} = a_i bi⊕bi+1=ai(其中 ⊕ \oplus ⊕ 表示按位异或运算符)。
输入
第一行包含一个整数 n n n( 2 ≤ n ≤ 2 ⋅ 1 0 5 2 \le n \le 2 \cdot 10^5 2≤n≤2⋅105)。
第二行包含 n − 1 n-1 n−1 个整数 a 1 , a 2 , … , a n − 1 a_1, a_2, \dots, a_{n-1} a1,a2,…,an−1( 0 ≤ a i ≤ 2 n 0 \le a_i \le 2n 0≤ai≤2n)。
输入的附加限制条件:始终可以从给定序列 a a a 构造出至少一个有效的数组 b b b。
输出
输出 n n n 个整数 b 1 , b 2 , … , b n b_1, b_2, \dots, b_n b1,b2,…,bn。如果存在多个满足条件的数组,可以输出其中任意一个。
思路
由 b i ⊕ b i + 1 = a i b_i \oplus b_{i+1}=a_i bi⊕bi+1=ai 得:
b 1 ⊕ b 2 = a 1 b_1 \oplus b_2=a_1 b1⊕b2=a1
b 2 ⊕ b 3 = a 2 b_2 \oplus b_3=a_2 b2⊕b3=a2
b 3 ⊕ b 4 = a 3 b_3 \oplus b_4=a_3 b3⊕b4=a3,异或累加得:
b 1 ⊕ b i = a 1 ⊕ a 2 ⊕ a 3 ⊕ . . . ⊕ a i − 1 b_1 \oplus b_i=a_1 \oplus a_2 \oplus a_3 \oplus ... \oplus a_{i-1} b1⊕bi=a1⊕a2⊕a3⊕...⊕ai−1,即:
b i = b 1 ⊕ a 1 ⊕ a 2 ⊕ a 3 ⊕ . . . ⊕ a i − 1 b_i=b_1 \oplus a_1 \oplus a_2 \oplus a_3 \oplus ... \oplus a_{i-1} bi=b1⊕a1⊕a2⊕a3⊕...⊕ai−1。
因为题目保证有解,所以 b 1 b_1 b1 存在某个取值,使得 b b b 中元素各不相同,即 a a a 的所有前缀异或和各不相同,且不存在 0 0 0。那么我们很容易得到:
对于 b 1 b_1 b1 的任意取值, b b b 中元素都互不相同。
因为 every integer from 0 0 0 to n − 1 n-1 n−1 appears in b b b exactly once,而我们已经知道了 b b b 中元素互不相同,现在的任务就是保证 b b b 中元素最小化。为了达到这一目的,我们只能修改 b 1 b_1 b1 的大小。
让 b 1 b_1 b1 的二进制第 k k k 位最优,使得 b 2 , . . . , b n b_2, ..., b_n b2,...,bn 中二进制第 k k k 位上的“1”的数量最小,进而使得 b b b 数组整体最小。这里使用了贪心的思路来实现(局部最优得到整体最优,二进制每一位最优得到二级制所有位最优)。
C o d e Code Code
#include <bits/stdc++.h>
#define int long long
#define sz(a) ((int)a.size())
#define all(a) a.begin(), a.end()
using namespace std;
using PII = pair<int, int>;
using i128 = __int128;
const int N = 2e5 + 10;int n;void solve(int Case) {cin >> n;vector <int> a(n + 1, 0);for (int i = 1; i <= n - 1; i ++) {cin >> a[i];a[i] ^= a[i - 1];}int b1 = 0;for (int i = 0; i <= 30; i ++) {int num1 = 0;int num0 = 0;for (int j = 1; j <= n - 1; j ++) {if (a[j] >> i & 1) {num1 ++;} else {num0 ++;}}if (num1 > num0) {b1 += 1 << i;}}cout << b1 << " ";for (int i = 2; i <= n; i ++) {cout << (a[i - 1] ^ b1) << " ";}cout << "\n";
}signed main() {cin.tie(0)->ios::sync_with_stdio(false);int T = 1;
// cin >> T; cin.get();int Case = 0;while (++ Case <= T) solve(Case);return 0;
}
相关文章:

【位运算】XOR Construction—CF1895D
XOR Construction—CF1895D 参考文章 翻译 题目要求构造一个长度为 n n n 的数组 b b b,满足以下条件: 数组 b b b 中包含从 0 0 0 到 n − 1 n-1 n−1 的每个整数,且每个整数仅出现一次;对于 i i i 从 1 1 1 到 n − …...
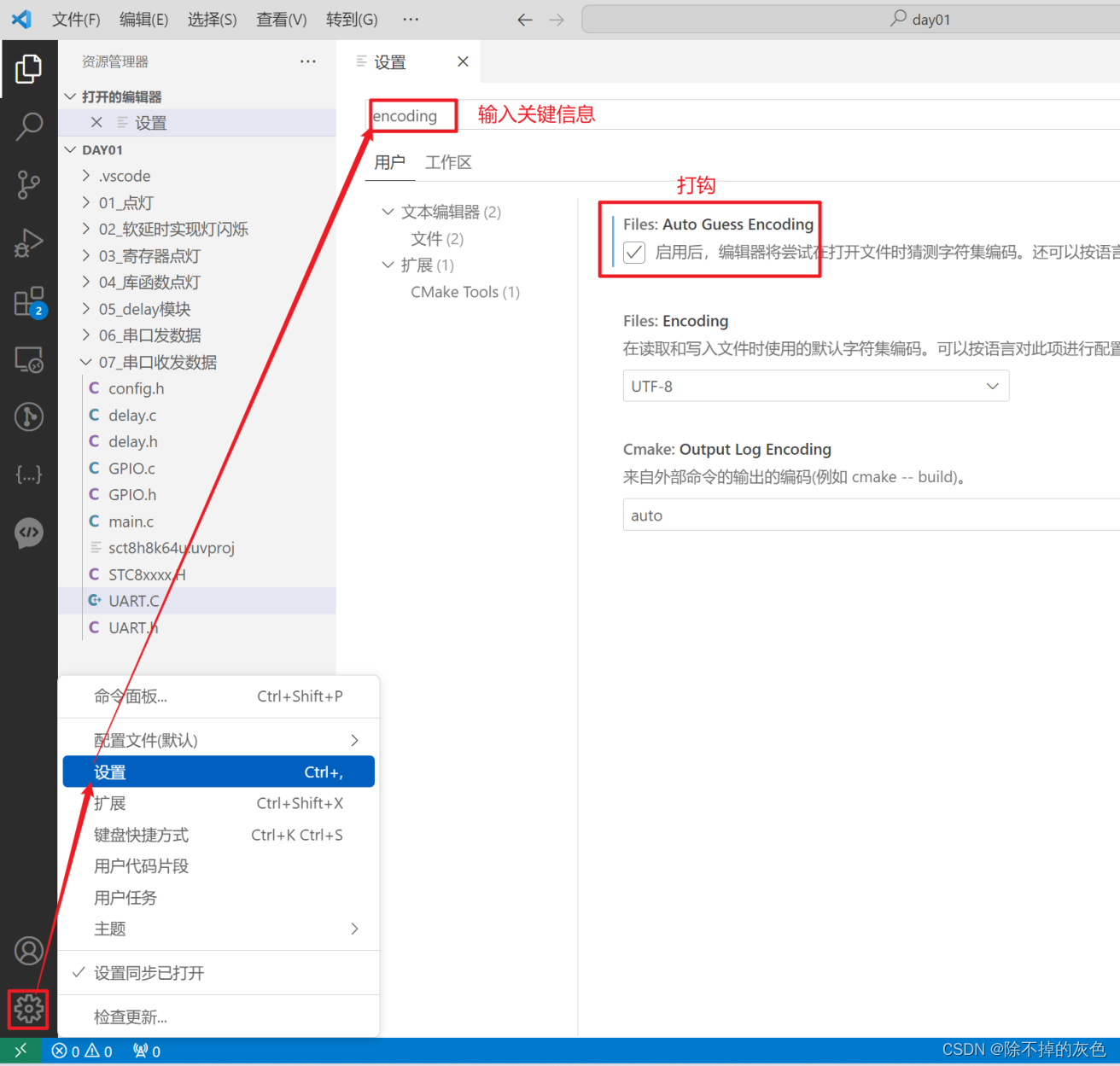
解决Visual Studio Code 控制台中文乱码问题
C和CPP运行编码指定 "code-runner.executorMap": {"c": "cd $dir && gcc -fexec-charsetGBK $fileName -o $fileNameWithoutExt && $dir$fileNameWithoutExt","cpp": "cd $dir && g -fexec-charsetGBK $…...

React Native自学笔记
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目…...

程序员笔记本电脑选 windows 还是 MAC
计算机选择是每个进入 IT 行业同学的第一个重要选择,那么你是怎么选择的呢? 选择操作系统(Windows还是macOS)取决于程序员的需求、偏好和工作流程。每个操作系统都有其优点和缺点,下面将分别讨论它们,以帮助…...
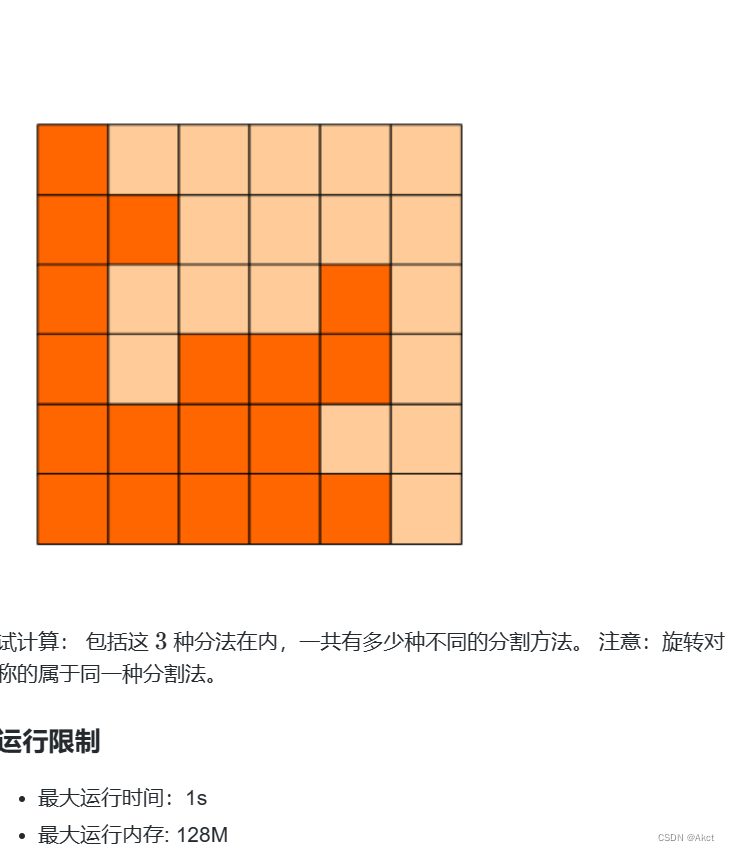
蓝桥杯每日一题2023.11.5
题目描述 方格分割 - 蓝桥云课 (lanqiao.cn) 题目分析 对于每个图我们可以从中间开始搜索,如果到达边界点就说明找到了一种对称的方法,我们可以直接对此进行答案记录每次进行回溯就会找到不同的图像,如果是一样的图像则算一种情况ÿ…...

多媒体应用设计师 2023年(含答案回忆版)
以下是小红书上的回忆版 软考考完疯狂回忆,多媒体应用设计师选择题 1.pattern 2.effective 3.merge 4.applications 5.graphic 6.udp 7.rtp 8.rtsp 9.10cm 10.永久 11…97 12.工作技术管理标准 13.管理型元数据 14.premiere 15.wave 16.500km/h 17.3M 18.44000 19.…...
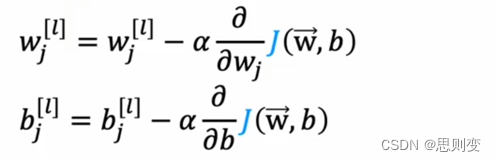
[Machine Learning][Part 8]神经网络的学习训练过程
目录 训练过程 一、建立模型: 二、建立损失函数 J(w,b): 三、寻找最小损失函数的(w,b)组合 为什么需要激活函数 激活函数种类 二分法逻辑回归模型 线性回归模型 回归模型 训练过程 一、建立模型: 根据需求建立模型,从前面神经网络的…...
Git 内容学习
一、Git 的理解 Git是一个分布式版本控制系统(Distributed Version Control System,简称 DVCS),用于对项目源代码进行管理和跟踪变更。分为两种类型的仓库:本地仓库和远程仓库。 二、Git 的工作流程 详解如下&#x…...
Zookeeper3.7.1分布式安装部署
上传安装文件到linux系统上面 解压安装文件到安装目录 [zhangflink9wmwtivvjuibcd2e package]$ tar -zxvf apache-zookeeper-3.7.1-bin.tar.gz -C /opt/software/3. 修改解压文件名 [zhangflink9wmwtivvjuibcd2e software]$ mv apache-zookeeper-3.7.1-bin/ zookeeper-3.7…...

CSS必学:元素之间的空白与行内块的幽灵空白问题
作者:WangMin 格言:努力做好自己喜欢的每一件事 CSDN原创文章 博客地址 👉 WangMin 我们在开发的过程中,难免会出现一些难以预料的问题。那么其中,CSS空白现象就是非常常见的问题之一。虽然它已经被发现很久,但仍然有许多新手和经…...

C++类中对构造函数的重载
C类中对构造函数的重载 C 允许在同一作用域中的某个函数和运算符指定多个定义,分别称为函数重载和运算符重载。 重载声明是指一个与之前已经在该作用域内声明过的函数或方法具有相同名称的声明,但是它们的参数列表和定义(实现)不…...

QtC++与QLabel详解
介绍 QLabel 类是Qt中的一个用于显示文本或图像的控件类,通常用于用户界面中以提供静态文本或图片显示的功能。以下是对QLabel在Qt中的作用的详细解释: 文本和图像显示: QLabel 可以用来显示文本和图像。这使得它成为显示标签、标题、说明或…...

090基于web+springboot的中小企业设备管理系统
欢迎大家关注,一起好好学习,天天向上 文章目录 一项目简介技术介绍 二、功能组成三、效果图四、 文章目录 一项目简介 本中小企业设备管理系统管理员有个人中心,用户管理,员工管理,设备信息管理,配件信息管…...
input 调起键盘 ,键盘距离输入框底部太近
input 调起键盘 ,键盘距离输入框底部太近 解决方法 cursorSpacing‘20’ 单位是 ‘px’ <input cursorSpacing20 type"text" v-model"replyMain" />距离底部距离 20px ,输入框距离键盘距离是20px...

前端深拷贝与浅拷贝的实现
1、浅拷贝和深拷贝的定义 1.1、浅拷贝 有两种方式,一种是把一个对象里面的所有的属性值和方法都复制给另一个对象,另一种是直接把一个对象赋给另一个对象,使得两个都指向同一个对象。浅拷贝对内存地址的复制,让目标对象指针和源…...
哆啦百宝箱APP
专门为年轻人设计的APP,主打的免费、无恶心广告、不获取任何个人信息。 哆啦百宝箱 ● 永久免费 ● 无恶心广告 ● 种类巨多 ● 全民参与 ● 爆款功能 ● 用心创造 哆啦百宝箱 提供了从日常、图片、查询、设备、趣味、娱乐等多方面的功能, 操作简单&a…...
lv9 嵌入式开发 数据库sqlite
1 数据库基本概念 数据(Data) 能够输入计算机并能被计算机程序识别和处理的信息集合 数据库 (Database) 数据库是在数据库管理系统管理和控制之下,存放在存储介质上的数据集合 2 常用的数据库 大型数据库…...

「Verilog学习笔记」异步复位的串联T触发器
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 分析 这道题目里我们有两个需要明确的点: 1. 什么是异步复位 2. 什么是串联的T触发器 关于第一个点,可以看我的这篇文章,已经整理好了&a…...

什么是51单片机,,如何写代码,并且烧录?
文章目录 1.单片机介绍2.Keil 5操作1.打开Keil 5 3 新建工程3.添加文件并写代码4.添加到group5,设置6.check7.编译8.打开头文件9 调整编辑器 4.烧录1.烧录程序2.串口查询 5.Debug1.首先编译2.调试3.查询 6 51单片机汇编指令1.格式2.符号3.寻址4.数据传送与交换指令5.交换指令6 …...

Multer 实现文件上传功能
Multer 实现文件上传功能 前言:Multer 安装和使用1、安装2、使用2-1 前端代码2-2 后端代码3、实现效果前言: post请求一般有4种数据类型: application/x-www-form-urlencodedmultipart/form-dataapplication/jsontext/xml相应后端Express会使用不同的中间件来解析不同类型的…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
