二叉搜索树(查找,插入,删除)
目录
1.概念
2.性质
3.二叉搜索树的操作
1.查找
2.插入
3.删除(难点)
1.概念
二叉搜索树又称二叉排序树.利用中序遍历它就是一个有顺序的一组数.
2.性质
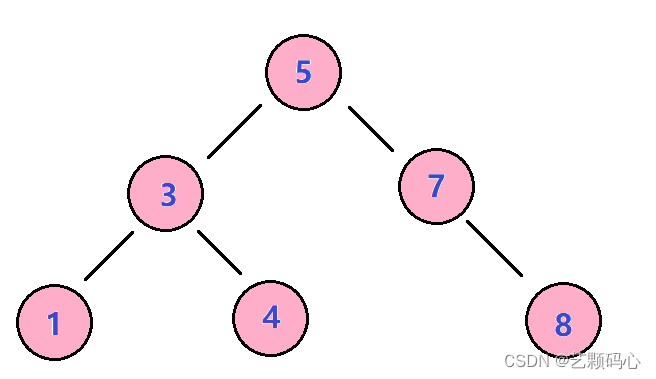
1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
2.若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
3.它的左右子树也分别为二叉搜索树
3.二叉搜索树的操作
1.查找
根据搜索树的性质来进行查找操作.
/*** 查找* @param root* @param val*/public TreeNode find(TreeNode root, int val) throws FindException{if (root == null) {throw new FindException("root 为空");}while (root != null) {if (root.val == val) {return root;} else if (root.val < val) {root = root.right;} else {root = root.left;}}return null;}2.插入
每次插入进去的值都在叶子节点.
如果插入的是相同的数那么直接return. (在搜索树中插入相同的数没有意义)
/*** 插入* @param root* @param val* @return*/public TreeNode insert(TreeNode root, int val) {if (root == null) {root = new TreeNode(val);return root;}TreeNode cur = root;TreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else {cur = cur.left;}}if (parent.val < val) {parent.right = new TreeNode(val);} else {parent.left = new TreeNode(val);}return root;}3.删除(难点)
对于删除我们要去判断3种情况 : 假设要删除的节点是cur
一 . cur.left == null 在这个前提下 还有三种情况:
1 . cur 是 root , root = cur.right;
2 . cur不是root, cur是parent.left ; parent.left = cur.right;
3 . cur不是root, cur是parent.right; parent.right = cur.right;

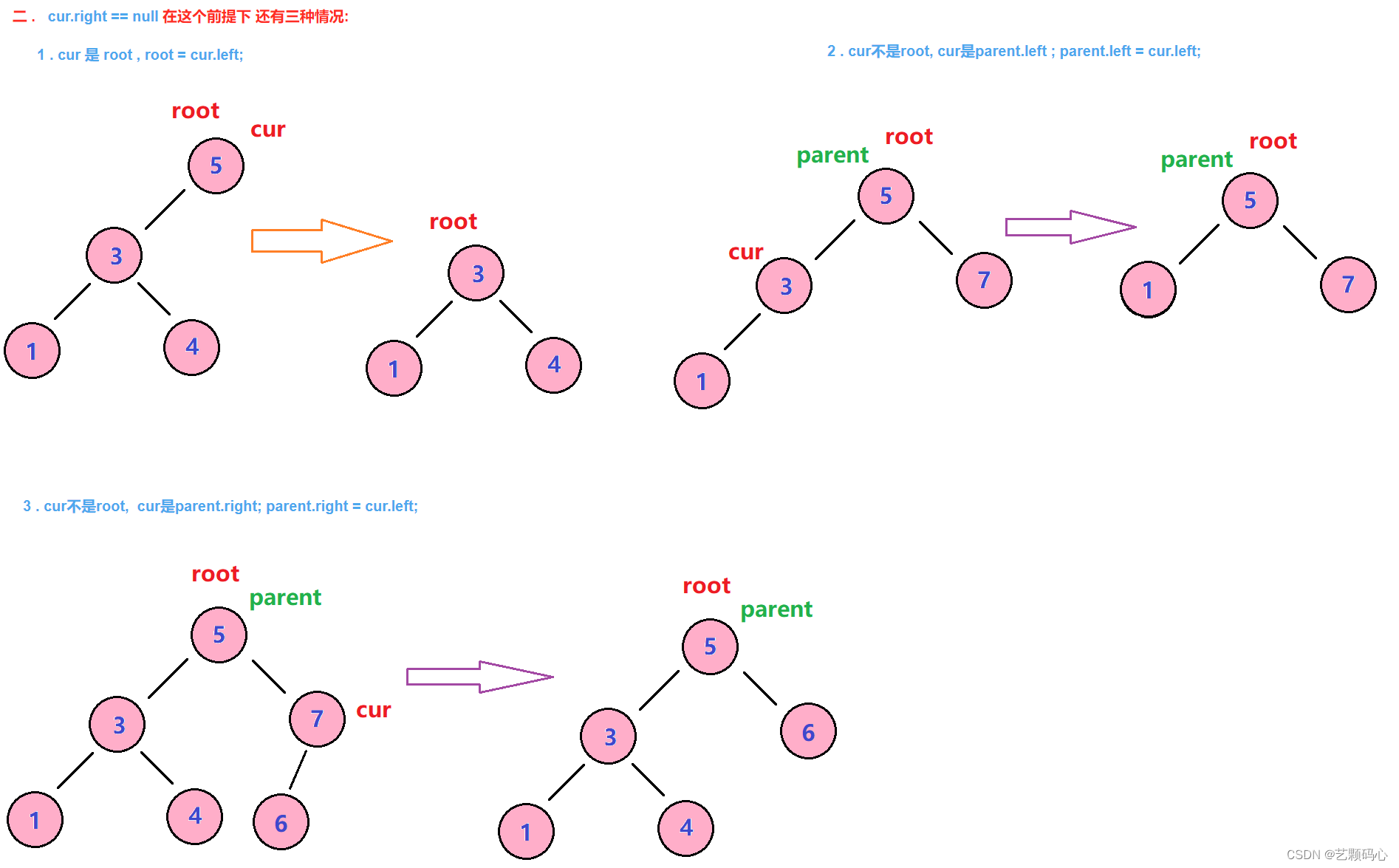
二 . cur.right == null 在这个前提下 还有三种情况:
1 . cur 是 root , root = cur.left;
2 . cur不是root, cur是parent.left ; parent.left = cur.left;
3 . cur不是root, cur是parent.right; parent.right = cur.left;
三 (重). cur 的左右都不为空 :
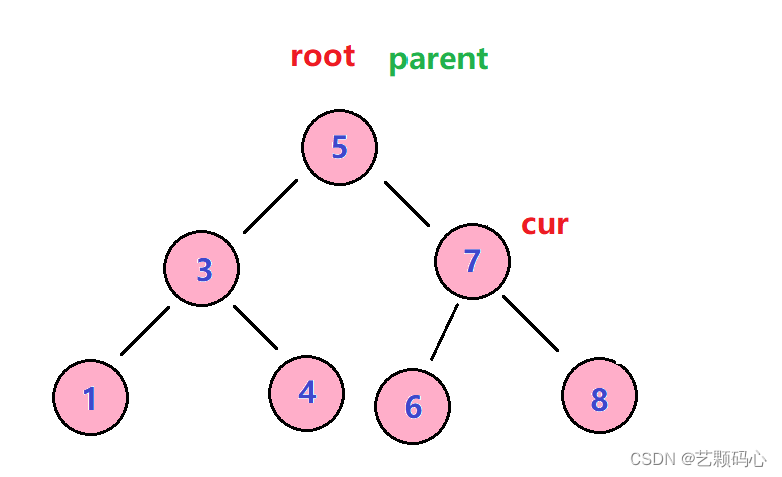
思路 : 假设要被删除的是cur , 我们去找到cur右树中最小的那个节点 . 把它的val值跟cur.val交换.
交换之后我们的任务就是去删除交换后的那个节点(之前右树中最小的值).
但是这样做的话还有一个问题 : 在我们去删被交换后的那个节点时,它的左子树肯定是空的.
比如是这样 :
第一种情况 :
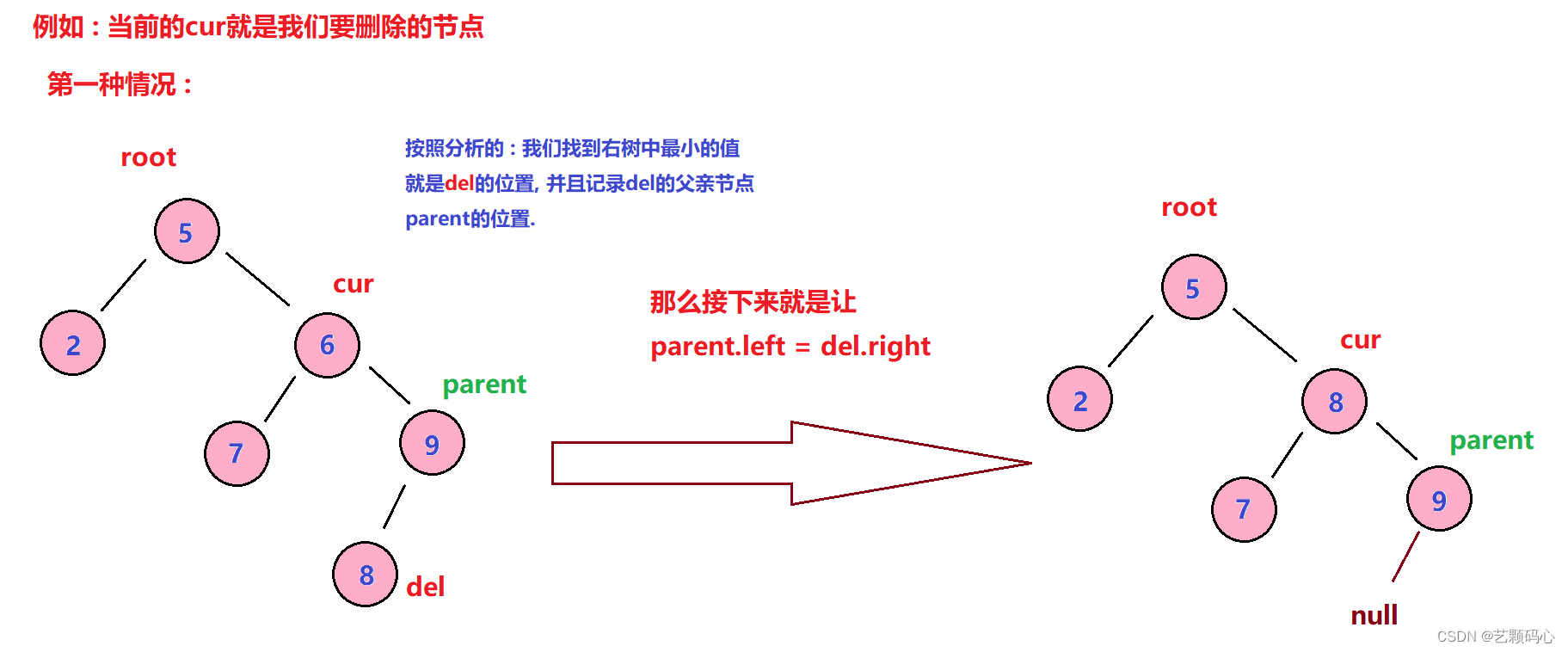
第二种情况 :

结合以上两种情况 : 我们就要去判断parent.left == del 还是 parent.right = del
代码实现 :
public class BinarySearchTree {static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}}/*** 查找* @param root* @param val*/public TreeNode find(TreeNode root, int val) throws FindException{if (root == null) {throw new FindException("root 为空");}while (root != null) {if (root.val == val) {return root;} else if (root.val < val) {root = root.right;} else {root = root.left;}}return null;}/*** 插入* @param root* @param val* @return*/public TreeNode insert(TreeNode root, int val) {if (root == null) {root = new TreeNode(val);return root;}TreeNode cur = root;TreeNode parent = null;while (cur != null) {parent = cur;if (cur.val < val) {cur = cur.right;} else {cur = cur.left;}}if (parent.val < val) {parent.right = new TreeNode(val);} else {parent.left = new TreeNode(val);}return root;}//中序遍历public void inorder(TreeNode root) {if (root == null) {return;}inorder(root.left);System.out.print(root.val + " ");inorder(root.right);}/*** 删除* @param root* @param val*/public void remove(TreeNode root, int val) {TreeNode cur = root;if (cur == null) {throw new RootNullException("root 为空");}TreeNode parent = null;while (cur != null) {if (cur.val == val) {del(cur,parent,root);break;} else if (cur.val < val) {parent = cur;cur = cur.right;} else {parent = cur;cur = cur.left;}}}//删除cur节点public void del(TreeNode cur, TreeNode parent, TreeNode root) {if (cur.left == null) {if (cur == root) {root = root.right;} else if (parent.right == cur) {parent.right = cur.right;} else {parent.left = cur.right;}} else if (cur.right == null) {if (cur == root) {root = root.left;} else if (parent.right == cur) {parent.right = cur.left;} else {parent.left = cur.left;}} else {//程序到这 就是cur的左右都不为空TreeNode del = cur.right;parent = cur;while (del.left != null) {parent = del;del = del.left;}cur.val = del.val;if (parent.right == del) {parent.right = del.right;} else {parent.left = del.right;}}}
}
以上就是关于搜索树的一些基本操作.
有任何问题可以私信我!
相关文章:

二叉搜索树(查找,插入,删除)
目录 1.概念 2.性质 3.二叉搜索树的操作 1.查找 2.插入 3.删除(难点) 1.概念 二叉搜索树又称二叉排序树.利用中序遍历它就是一个有顺序的一组数. 2.性质 1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 2.若它的右子树不为空,则右子树上所有节点的值都…...

C# PictureEdit 加载图片
方法一: 如果要加载的图片的长宽比不是太过失衡, 1.可以改变picturebox的SizeMode属性为 PictureBoxSizeMode.StretchImage, 2.或者Dev控件 PictureEdit的SizeMode属性为Zoom。(zoom:缩放;clip剪短;stret…...
3种方法设置PDF“打开密码”,总有一种适合你
PDF文件是我们工作中经常用到的文件之一,对于重要的文件,设置“打开密码”是一种很好的保护方式。下面就来说说,设置PDF“打开密码”有哪三种方法? 方法一:在线网站加密 市面上有很多可以直接在线上加密PDF文件的产品…...
-计算机网络(笔记))
第三章 数据链路层(点到点的传输服务)-计算机网络(笔记)
计算机网络 第三章 数据链路层(点到点的传输服务) 数据链路层属于计算机网络的低层。数据链路层使用的信道主要有以下两种类型: (1)点到点信道。这种信道使用一对一的点到点通信方式。 (2)广…...

volatile关键字与CAS机制
volatile关键字 volatile关键字可以对类的成员变量与静态变量进行修饰 volatile关键字的作用 1.保证被修饰属性的可见性,被修饰后的属性如果被更改后其他线程是会立即可见的 2.保证被修饰属性的有序性,被修饰后的属性禁止修改指令执行的顺序 注意:volatile关键字不能保证属性…...

LeetCode题解 动态规划(四):416 分割等和子集;1049 最后一块石头的重量 II
背包问题 下图将背包问题做了分类 其中之重点,是01背包,即一堆物件选哪样不选哪样放入背包里。难度在于,以前的状态转移,多只用考虑一个变量,比如爬楼梯的阶层,路径点的选择,这也是能用滚动数组…...

【FFMPEG源码分析】从ffplay源码摸清ffmpeg框架(二)
demux模块 从前面一篇文章中可以得知,demux模块的使用方法大致如下: 分配AVFormatContext通过avformat_open_input(…)传入AVFormatContext指针和文件路径,启动demux通过av_read_frame(…) 从AVFormatContext中读取demux后的audio/video/subtitle数据包…...
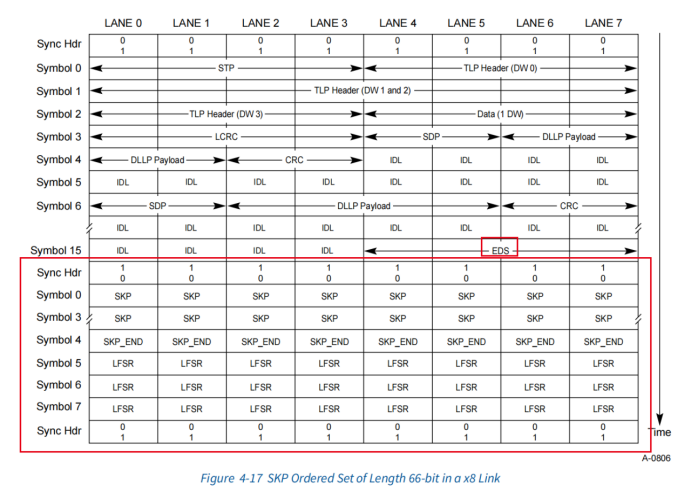
PCIE 学习笔记(入门简介)
PCIE 学习笔记书到用时方恨少啊,一年前学PCIE的笔记,再拿出来瞅瞅。发到博客上,方便看。PCIE基础PCIE和PCI的不同PCIE采用差分信号传输,并且是dual-simplex传输——每条lane上有TX通道和RX通道,所以每条lane上的信号是…...
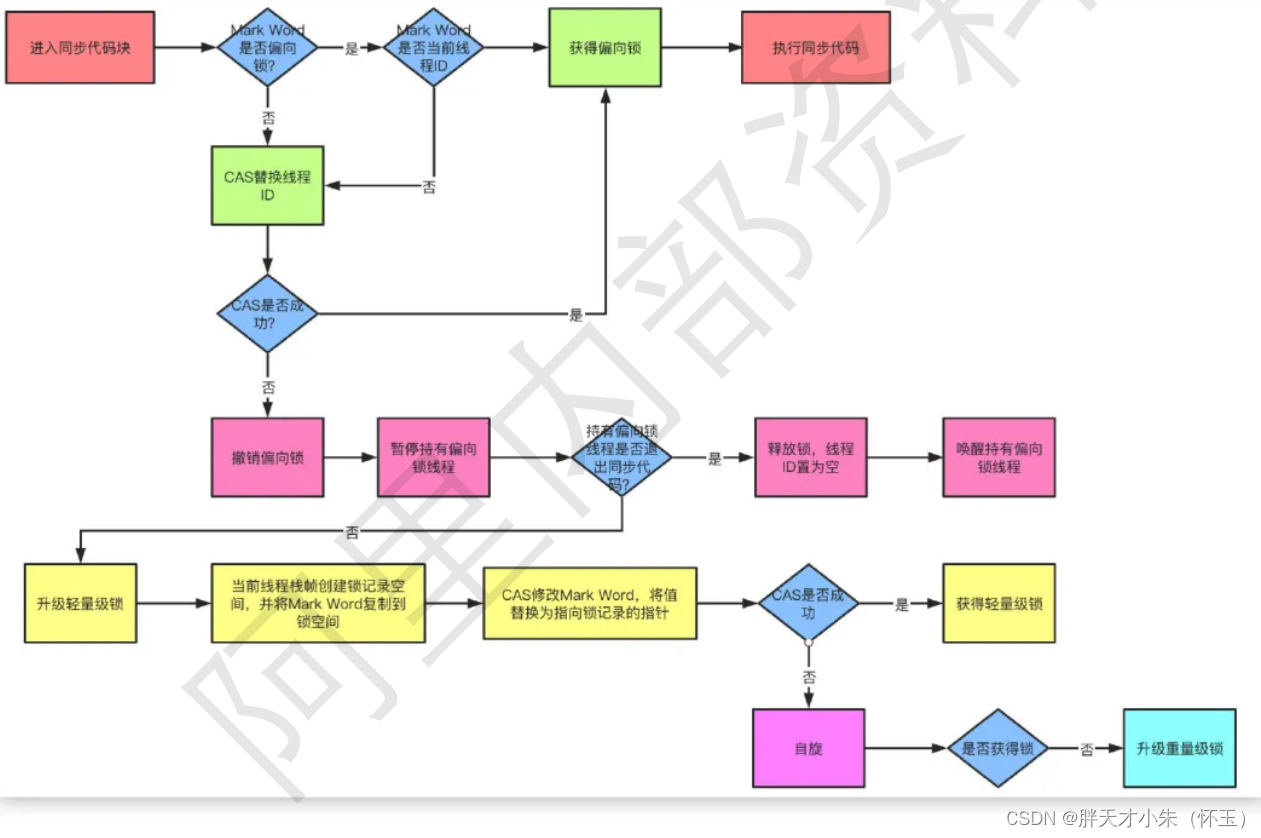
锁的优化机制了解嘛?请进!
点个关注,必回关 文章目录自旋锁:自适应锁:锁消除:锁粗化:偏向锁:轻量级锁:从JDK1.6版本之后,synchronized本身也在不断优化锁的机制,有些情况下他并不会是一个很重量级的…...

5.点赞功能 Redis
Redis(1)简介Redis 是一个高性能的 key-value 数据库原子 – Redis的所有操作都是原子性的。多个操作也支持事务,即原子性,通过MULTI和EXEC指令包起来。非关系形数据库数据全部存在内存中,性能高。(2&#…...
)
Java序列化和反序列化(详解)
一、理解Java序列化和反序列化 Serialization(序列化):将java对象以一连串的字节保存在磁盘文件中的过程,也可以说是保存java对象状态的过程。序列化可以将数据永久保存在磁盘上(通常保存在文件中)。 deserialization(反序列化):将保存在磁…...

【刷题篇】链表(上)
前言🌈前段时间我们学习了单向链表和双向链表,本期将带来3道与链表相关的OJ题来巩固对链表的理解。话不多说,让我们进入今天的题目吧!🚀本期的题目有:反转单链表、链表的中间结点、合并两个有序链表反转单链…...

ConcurrentHashMap设计思路
ConcurrentHashMap设计思路Hashtable vs ConcurrentHashMapHashtable vs ConcurrentHashMap Hashtable 对比 ConcurrentHashMap Hashtable 与 ConcurrentHashMap 都是线程安全的 Map 集合Hashtable 并发度低,整个 Hashtable 对应一把锁,同一时刻&#…...

Unity基于GraphView的行为树编辑器
这里写自定义目录标题概述基于GitHub上:目前这只是做了一些比较基础的功能节点开发,仅仅用于学习交流,非完成品。项目GitHub连接:[https://github.com/HengyuanLee/BehaviorTreeExamples](https://github.com/HengyuanLee/Behavio…...
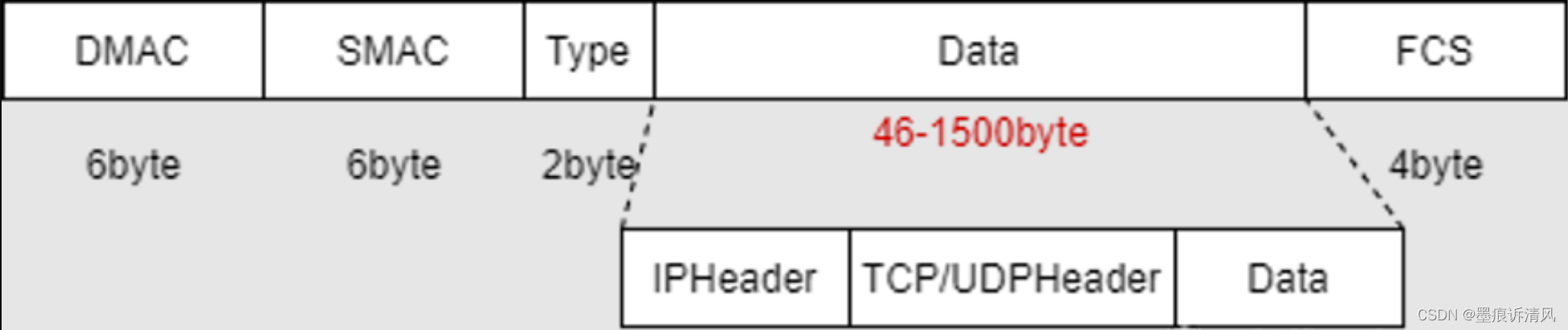
网络流量传输MTU解析
基本概念 以太网的链路层对数据帧的长度会有一个限制,其最大值默认是1500字节,链路层的这个特性称为MTU,即最大传输单元 Maximum Transmission Unit,最大传输单元,指的是数据链路层的最大payload,由硬件网…...
)
30个HTML+CSS前端开发案例(四)
30个HTMLCSS前端开发案例(17-20)鼠标移入文字加载动画效果代码实现效果鼠标悬停缩放效果实现代码效果鼠标移入旋转动画实现代码效果loding加载动画实现代码效果资源包鼠标移入文字加载动画效果 代码实现 <!DOCTYPE html> <html><head&g…...

《TPM原理及应用指南》学习 —— TPM执行环境3
本文对应《A Practical Guide to TPM 2.0 — Using the Trusted Platform Module in the New Age of Security》的第6章第3节。 6.3 Summary —— 总结 Now that you have an execution environment (or maybe both of them) set up, you’re ready to run the code samples f…...
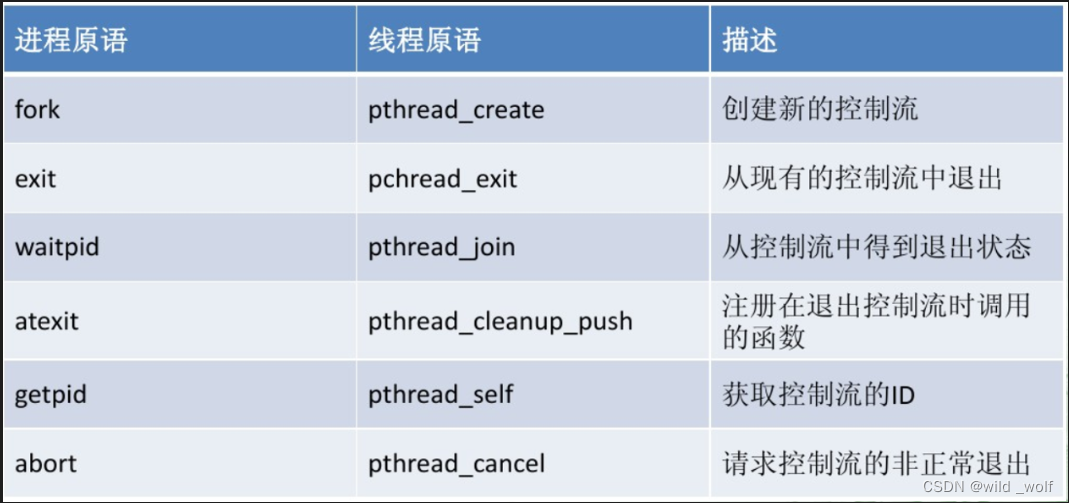
实验名称:经典同步问题:生成者与消费者问题
实验名称:经典同步问题:生成者与消费者问题 相关知识 信号量 信号量是用来协调不同进程间的数据对象,可用来保护共享资源,也能用来实现进程间及同一进程不同线程间的进程同步。分为二值信号灯和计算信号灯两种类型。 进程与线…...

EasyCVR视频云存储的架构解析与Sharelist云存挂载方法介绍
一、什么是视频云存储? 视频云存储主要用于为上层应用提供视频文件、结构化信息、事件信息的相关服务。云存储节点分为数据文件存储节点和结构化数据存储节点。数据文件存储节点主要用于视频、图片的存储。结构化数据存储节点用于存储结构化数据并提供相关服务。 …...
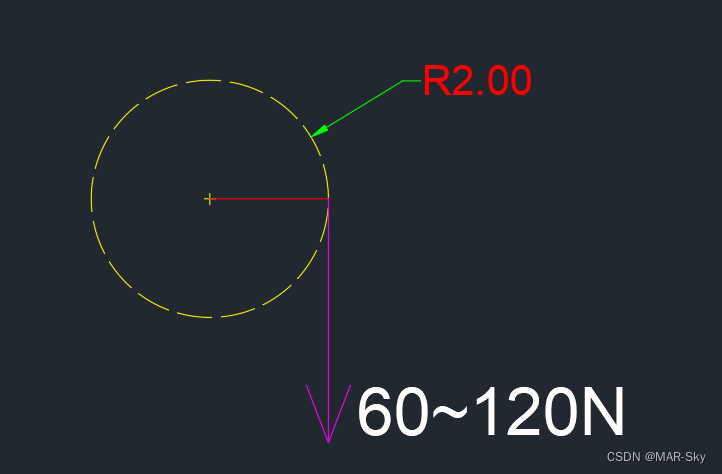
电机参数中力矩单位kgf.cm,Nm,mNm表示的含义
力的基本知识 质量和力的比例系数 质量和重力的关系有一个重力系数:g≈9.8 N/kg≈10,后面看到的1kgf就相当于1kg物体的力也就是10N 杠杆原理 对于同一个支点,在不考虑杠杆的重量的情况下,实现同样的作用效果,距离支点越近&…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
