数据结构(超详细讲解!!)第二十一节 特殊矩阵的压缩存储
1.压缩存储的目标
值相同的元素只存储一次
压缩掉对零元的存储,只存储非零元
特殊形状矩阵:
是指非零元(如值相同的元素)或零元素分布具有一定规律性的矩阵。
如: 对称矩阵 上三角矩阵 下三角矩阵 对角矩阵 准对角矩阵
2.三角矩阵
三角矩阵大体分为三类:下三角矩阵、上三角矩阵和对称矩阵。
对于一个n阶矩阵A来说,若当i<j时,有aij=0,则称此矩阵为下三角矩阵;
若当i>j时,有aij=0,则称此矩阵为上三角矩阵;
若矩阵中的所有元素均满足aij=aji,则称此矩阵为对称矩阵。

对于下三角矩阵的压缩存储,我们只存储下三角的非零元素,对于零元素则不存。我们按“行序为主序”进行存储,得到的序列是a11, a21, a22, a31, a32, a33, …, an1, an2, …, ann。由于下三角矩阵的元素个数为n(n+1)/2,即:

所以可压缩存储到一个大小为n(n+1)/2的一维数组C中

下三角矩阵中元素aij(i>j)在一维数组A中的位置为:
Loc[i, j]=Loc[1, 1]+前i-1行非零元素个数+第i行中aij前非零元素个数
前i-1行元素个数=1+2+3+4+…+(i-1)=i(i-1)/2,所以有 Loc[i, j]=Loc[1, 1]+i(i-1)/2+j-1
同样,对于上三角矩阵,也可以将其压缩存储到一个大小为n(n+1)/2的一维数组C中。其中元素aij(i<j)在数组C中的存储位置为: Loc[i, j]=Loc[1, 1]+j(j-1)/2+i-1
对于对称矩阵,因其元素满足aij=aji,我们可以为每一对相等的元素分配一个存储空间,即只存下三角(或上三角)矩阵,从而将n2个元素压缩到n(n+1)/2个空间中。
3.带状矩阵
三对角带状矩阵有如下特点:
i=1, j=1, 2
1<i<n, j=i-1, i, i+1;
i=n, j=n-1, n;
时,aij非零,其它元素均为零。

(1)确定存储该矩阵所需的一维向量空间的大小
在这里我们假设每个非零元素所占空间的大小为1个单元。 从图中观察得知,三对角带状矩阵中,除了第一行和最后一行只有2个非零元素外,其余各行均有3个非零元素。由此得到, 所需一维向量空间的大小为 2+2+3(n-2)=3n-2

(2)确定非零元素在一维数组空间中的位置
Loc[i , j] = Loc[1, 1]+前i-1行非零元素个数+第i行中aij前非零元素个数;
前i-1行元素个数=3×(i-1)-1(因为第1行只有2个非零元素);
第i行中aij前非零元素个数=j-i+1,其中

由此得到:
Loc[i, j]=Loc[1, 1]+3(i-1)-1+j-i+1 =Loc[1, 1]+2(i-1)+j-1
4.稀疏矩阵
是指非零元比零元少得多,且非零元在矩阵中的分布不具有一定规律性的矩阵。

假设 m 行 n 列的矩阵含 t 个非零元素,则称

为稀疏因子。 通常认为 小于等于0.05 的矩阵为稀疏矩阵。
(1)稀疏矩阵的三元组表表示法
对于矩阵中的每个非零元,可以用三个属性来惟一确定:它所在的行、所在的例以及它的值。因此,可以用一个三元组(行, 列, 值)来惟一确定矩阵中的一个非零元。


稀疏矩阵的三元组表表示法虽然节约了存储空间, 但比起矩阵正常的存储方式来讲,其实现相同操作要耗费较多的时间, 同时也增加了算法的难度, 即以耗费更多时间为代价来换取空间的节省。
#define MAXSIZE 1000 /*非零元素的个数最多为1000*/ typedef struct {int row, col; /*该非零元素的行下标和列下标*/ElementType e; /*该非零元素的值*/ }Triple; typedef struct {Triple data[MAXSIZE+1]; /* 非零元素的三元组表,data[0]未用*/int m, n, len; /*矩阵的行数、 列数和非零元素的个数*/
}TSMatrix;
1) 用三元组表实现稀疏矩阵的转置运算
下面首先以稀疏矩阵的转置运算为例,介绍采用三元组表时的实现方法。
所谓的矩阵转置,是指变换元素的位置,把位于(row,col)位置上的元素换到(col,row)位置上,也就是说, 把元素的行列互换。
采用矩阵的正常存储方式时, 实现矩阵转置的经典算法如下:
void TransMatrix(ElementType source[n][m], ElementType dest[m][n])
{/*source和dest分别为被转置的矩阵和转置以后的矩阵(用二维数组表示)*/ int i, j; for(i=0; i<m; i++)for (j=0; j< n; j++) dest[i][ j]=source[j] [i] ; }
采用矩阵的三元组存储方式实现转置
① 矩阵source的三元组表A的行、 列互换就可以得到B中的元素

② 为了保证转置后的矩阵的三元组表B也是以“行序为主序”进行存放,则需要对行、列互换后的三元组表B按B的行下标(即A的列下标)大小重新排序

方法一:

我们附设一个位置计数器j,用于指向当前转置后元素应放入三元组表B中的位置。 处理完一个元素后,j加1, j的初值为1。 具体转置算法如下:
Void TransposeTSMatrix(TSMatrix A, TSMatrix *B)
{ /*把矩阵A转置到B所指向的矩阵中去, 矩阵用三元组表表示 */int i , j, k ; B->m= A.n ; B->n= A.m ; B->len= A.len ; if(B->len>0){
j=1; for(k=1; k<=A.n; k++) for(i=1; i<=A.len; i++) if(A.data[i].col==k) { B->data[j].row=A.data[i].col B->data[j].col=A.data[i].row; B->data[j].e=A.data[i].e; j++; }}
}
算法的时间耗费主要是在双重循环中,其时间复杂度为O(A.n×A.len), 最坏情况下,当A.len=A.m×A.n时,时间复杂度为O(A.m×A.n2)。采用正常方式实现矩阵转置的算法时间复杂度为O(A.m×A.n)。
方法二:
为了能将待转置三元组表A中元素一次定位到三元组表B的正确位置上,需要预先计算以下数据:
(1) 待转置矩阵source每一列中非零元素的个数(即转置后矩阵dest每一行中非零元素的个数)。
(2) 待转置矩阵source每一列中第一个非零元素在三元组表B中的正确位置(即转置后矩阵dest每一行中第一个非零元素在三元组B中的正确位置)。
为此, 需要设两个数组num[ ]和position[ ],其中num[col]用来存放三元组表A中第col列中非零元素个数(三元组表B中第col行非零元素的个数),position[col]用来存放转置前三元组表A中第col列(转置后三元组表B中第col行)中第一个非零元素在三元组表B中的正确位置。
num[col]的计算方法: 将三元组表A扫描一遍,对于其中列号为k的元素,给相应的num[k]加1。
position[col]的计算方法: position[1]=1, position[col]=position[col-1]+num[col-1], 其中2≤col≤A.n。

将三元组表A中所有的非零元素直接放到三元组表B中正确位置上的方法:
position[col]的初值为三元组表A中第col列(三元组表B的第col行)中第一个非零元素的正确位置,当三元组表A中第col列有一个元素加入到三元组表B时,则position[col]=position[col]+1,即: 使position[col]始终指向三元组表A中第col列中下一个非零元素的正确位置。
具体算法如下:
FastTransposeTSMatrix (TSMatrix A, TSMatrix * B)
{ /*基于矩阵的三元组表示, 采用快速转置法, 将矩阵A转置为B所指的矩阵*/
int col, t, p, q;
int num[MAXSIZE], position[MAXSIZE];
B->len=A.len; B->n=A.m; B->m=A.n;
if(B->len){
for(col=1; col<=A.n; col++) num[col]=0; for(t=1; t<=A.len; t++) num[A.data[t].col]++; /*计算每一列的非零元素的个数*/position[1]=1; for(col=2; col<A.n; col++) /*求col列中第一个非零元素在B.data[ ]中的正
确位置 */position[col]=position[col-1]+num[col-1]; for(p=1; p<A.len.p++) { col=A.data[p].col; q=position[col]; B->data[q].row=A.data[p].col; B->data[q].col=A.data[p].row; B->data[q].e=A.data[p].eposition[col]++; }
}
}
快速转置算法的时间主要耗费在四个并列的单循环上,这四个并列的单循环分别执行了A.n,A.len,A.n-1,A.len次,因而总的时间复杂度为O(A.n)+O(A.len)+O(A.n)+O(A.len),即为O(A.n+A.len)。 当待转置矩阵M中非零元素个数接近于A.m×A.n 时,其时间复杂度接近于经典算法的时间复杂度O(A.m×A.n)。
快速转置算法在空间耗费上除了三元组表所占用的空间外,还需要两个辅助向量空间,即num[1..A.n],position[1..A.n]。可见,算法在时间上的节省,是以更多的存储空间为代价的。
(2)稀疏矩阵的链式存储结构: 十字链表
与用二维数组存储稀疏矩阵比较,用三元组表表示的稀疏矩阵节约了空间,但是在进行矩阵加法、减法和乘法等运算时,有时矩阵中的非零元素的位置和个数会发生很大的变化。如A=A+B, 将矩阵B加到矩阵A上,此时若还用三元组表表示法,势必会为了保持三元组表“以行序为主序”而大量移动元素。
在十字链表中,矩阵的每一个非零元素用一个结点表示, 该结点除了(row,col,value)以外,还要有以下两个链域:
right: 用于链接同一行中的下一个非零元素;
down: 用于链接同一列中的下一个非零元素。
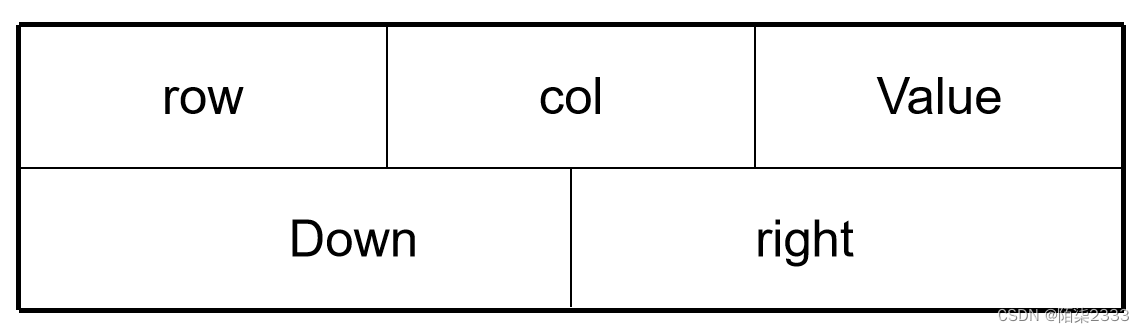
用两个一维的指针数组分别存放各行链表的头指针和各列链表的头指针,从而得到了矩阵的十字链表存储结构。
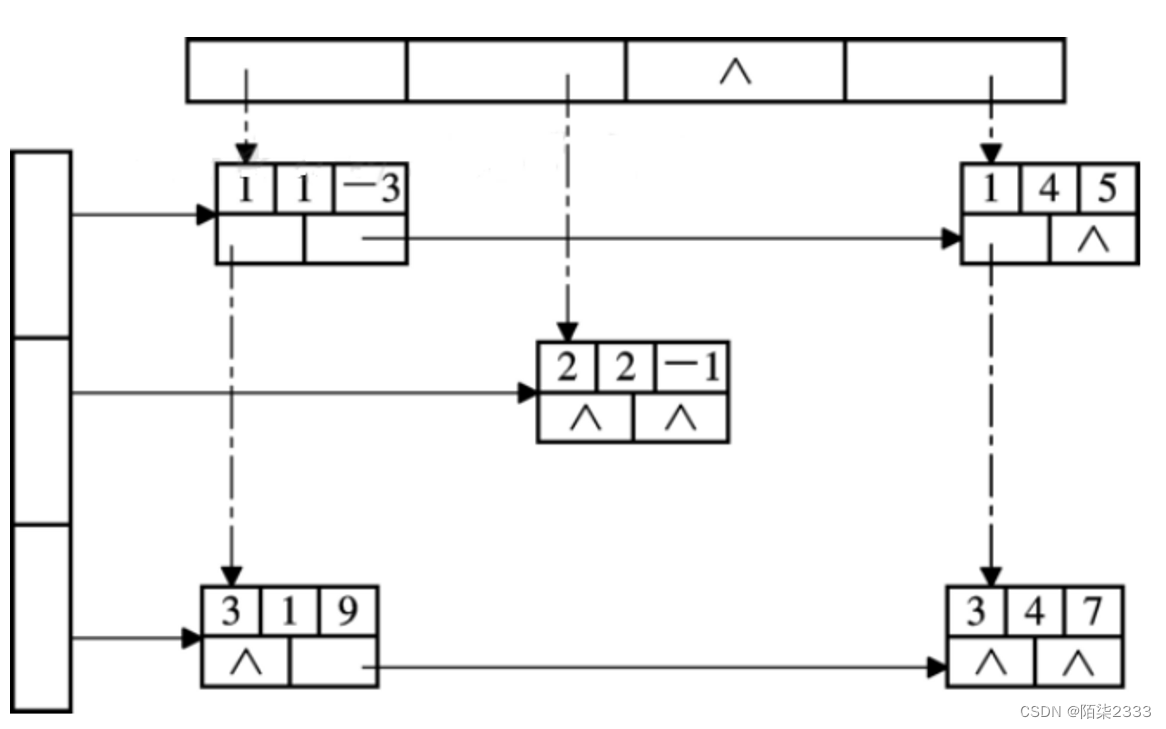
结构类型:
建十字链表的算法的时间复杂度为O(t×s),s=max(m,n)。
typedef struct OLNode{int row, col; /* 非零元素的行和列下标 */ ElementType value; struct OLNode * right, *down; /* 非零元素所在行表、列表的后继链域 */}OLNode; *OLink; typedef struct { OLink * row-head, *col-head; /* 行、 列链表的头指针向量 */ int m, n, len; /* 稀疏矩阵的行数、 列数、 非
零元素的个数 */}CrossList; CreateCrossList (CrossList * M){/* 采用十字链表存储结构, 创建稀疏矩阵M */if(M!=NULL) free(M); scanf(&m, &n, &t); /* 输入M的行数, 列数和非零元素的个数 */M->m=m; M->n=n; M->len=t; If(!(M->row-head=(OLink * )malloc((m+1)sizeof(OLink)))) exit(OVERFLOW); If(!(M->col-head=(OLink * )malloc((n+1)sizeof(OLink)))) exit(OVERFLOW); M->row-head[ ]=M->col-head[ ]=NULL;/* 初始化行、 列头指针向量, 各行、 列链表为空的链表 */for(scanf(&i, &j, &e); i!=0; scanf(&i, &j, &e)) { if(!(p=(OLNode *) malloc(sizeof(OLNode)))) exit(OVERFLOW); p->row=i; p->col=j; p->value=e; /* 生成结点 */ if(M->row-head[i]==NULL) M->row-head[i]=p;
else{ /* 寻找行表中的插入位置 */for(q=M->row-head[i]; q->right&&q->right->col<j; q=q->right)p->right=q->right; q->right=p; /* 完成插入 */ } if(M->col-head[j]==NULL) M->col-head[j]=p; else{ /*寻找列表中的插入位置*/for(q=M->col-head[j]; q->down&&q->down->row<i; q=q->down) p->down=q->down; q->down=p; /* 完成插入 */ }}}
相关文章:

数据结构(超详细讲解!!)第二十一节 特殊矩阵的压缩存储
1.压缩存储的目标 值相同的元素只存储一次 压缩掉对零元的存储,只存储非零元 特殊形状矩阵: 是指非零元(如值相同的元素)或零元素分布具有一定规律性的矩阵。 如: 对称矩阵 上三角矩阵 下三角矩阵 对角矩阵 准…...

Python最强自动化神器Playwright!再也不用为爬虫逆向担忧了!
版权说明:本文禁止抄袭、转载,侵权必究! 目录 一、简介+使用场景二、环境部署(准备)三、代码生成器(优势)四、元素定位器(核心)五、追踪查看器(辅助)六、权限控制与认证(高级)七、其他重要功能(进阶)八、作者Info一、简介+使用场景 Playwright是什么?来自Chat…...

为什么 conda 不能升级 python 到 3.12
为什么 conda 不能升级 python 到 3.12 2023-11-05 23:33:29 ChrisZZ 1. 目的 弄清楚为什么执行了如下升级命令后, python 版本还是 3.11? conda update conda conda update python2. 原因 因为 conda forge 没有完成 migration Migration is the …...
0X02
web9 阐释一波密码,依然没有什么 发现,要不扫一下,或者看一看可不可以去爆破密码 就先扫了看看,发现robots.txt 访问看看,出现不允许被访问的目录 还是继续尝试访问看看 就可以下载源码,看看源码 <?php $fl…...

【手写数据库所需C语言基础】可变结构体,结构体成员计算,类型强制转换为统一类型,数据库中使用C语言方法和技巧
专栏内容: 手写数据库toadb 本专栏主要介绍如何从零开发,开发的步骤,以及开发过程中的涉及的原理,遇到的问题等,让大家能跟上并且可以一起开发,让每个需要的人成为参与者。 本专栏会定期更新,…...
)
Android Studio(适配器Adapter)
认识适配器 在学完并且在做了一个自主项目后,我对适配器有了以下认识:1. 适配器的作用: 数据驱动的动态页面列表渲染,所以适配器主要就做了两件事:遍历数据,渲染页面(列表项)。比…...

携程AI布局:三重创新引领旅游行业智能化升级
2023年10月24日,携程全球合作伙伴峰会在新加坡召开,携程集团联合创始人、董事局主席梁建章做了名为《旅游业是独一无二的最好的行业》的演讲,梁建章在演讲中宣布了携程生成式 AI、内容榜单、ESG 低碳酒店标准三重创新的战略方向。这些创新将为…...

IOS手机耗电量测试
1. 耗电量原始测试方法 1.1 方法原理: 根据iPhone手机右上角的电池百分比变化来计算耗电量。 1.2实际操作: 在iOS通用设置中打开电池百分比数值显示,然后操作30分钟,60分钟,90分钟,看开始时和结束时电池…...
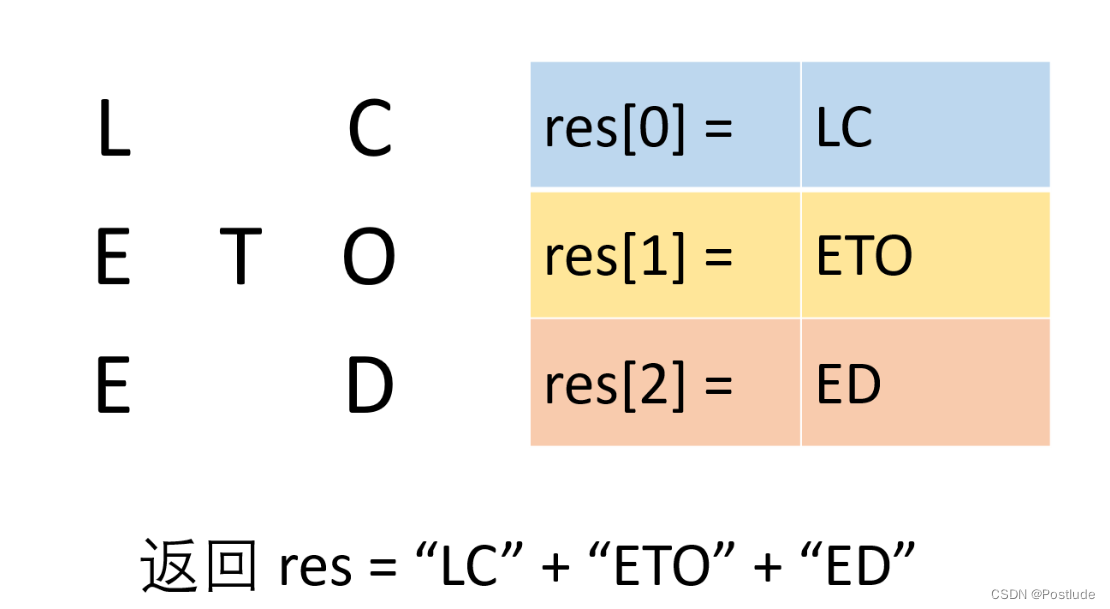
LeetCode.6 N字形变换
一开始想的是真的创建一个数组 去按照题目所给的要求填入数据 最后输出不为空的数组项 但是不仅时间复杂度高 而且错误频繁出现 最终也没有提交成功 查阅题解后发现数组并不重要 假设我们忽略掉数组中的那些空白项 最终输出的结果就是numRows行的字符串的拼接 string conver…...

第一章 03Java入门-编写第一个Java程序HelloWorld以及JVM、JDK和JRE概念
文章目录 前言一、下载和安装JDK二、第一个程序HelloWorld1.用记事本编写程序2.编译文件3.运行程序三、HelloWorld案例常见问题四、环境变量五、Notepad软件的安装和使用六、Java语言的发展七、Java为什么这么火八、JRE和JDK总结前言 上次我们学习了常见的CMD指令以及环境变量…...

windbg的常见调试命令
windbg的常见调试命令 1).break:在指定的条件下停止调试。 2).bt:显示调用堆栈信息。 3).catch:设置异常捕获,可以用来捕获程序中的异常并进行调试。 4).continue:继续执…...
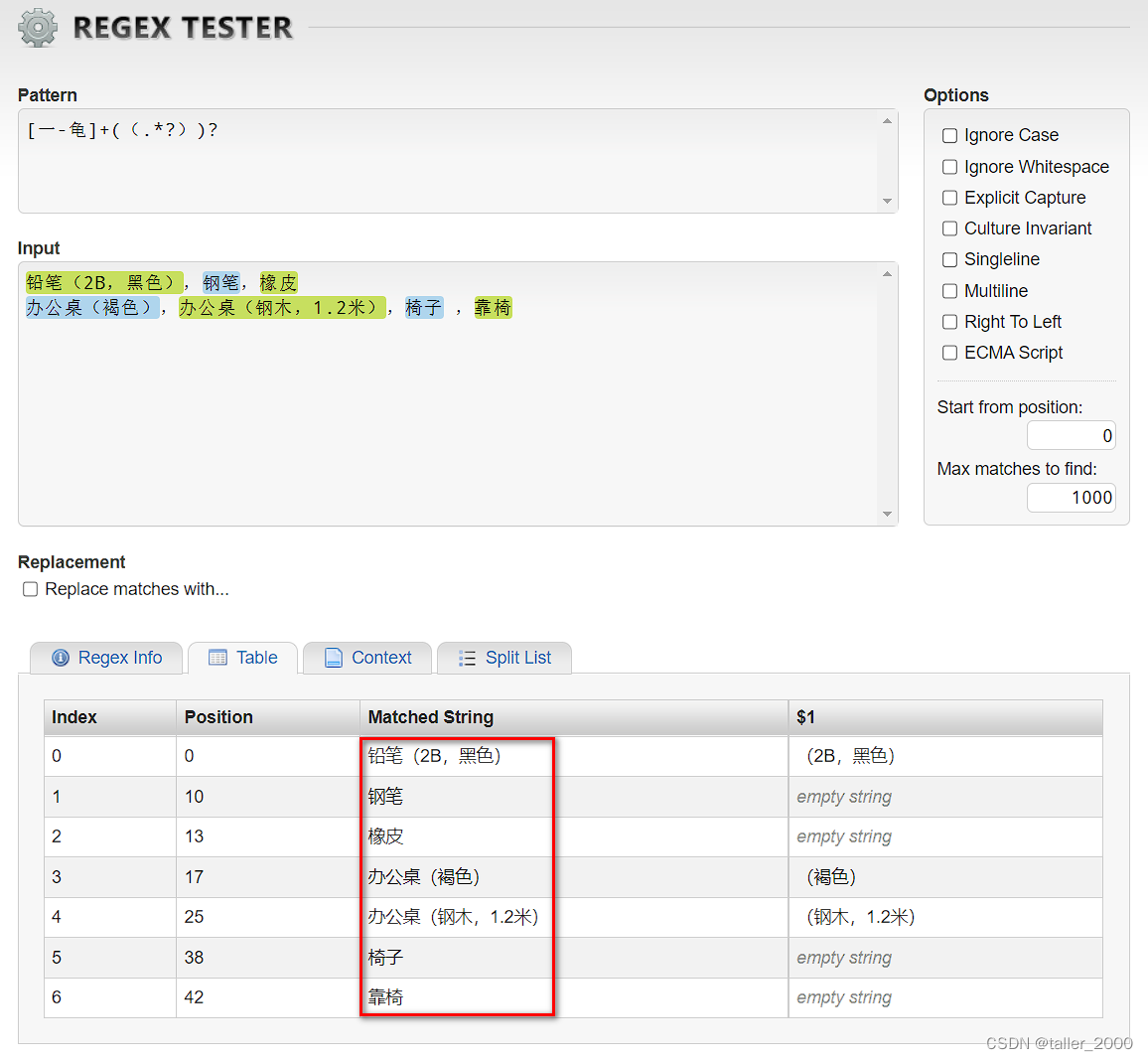
VBA之正则表达式(44)-- 拆分商品和规格
实例需求:商品组清单保存在A列中,现需要将其拆分为商品名称,保存在从B列开始的后续单元格中,部分商品包含规格,并且多种规格属性使用了逗号分隔,因此无法直接使用Excel分列功能完成数据拆分。 示例代码如下…...
听GPT 讲Rust源代码--library/std(13)
题图来自 Decoding Rust: Everything You Need to Know About the Programming Language[1] File: rust/library/std/src/os/horizon/raw.rs 在Rust源代码中,rust/library/std/src/os/horizon/raw.rs这个文件的作用是为Rust的标准库提供与Horizon操作系统相关的原始…...
)
计算机视觉任务图像预处理之去除图像中的背景区域-------使用连通域分析算法(包含完整代码)
原理 通过连通域分析算法能够找到最大的连通域,即图片的主体部分,然后保存该连通域的最小外接矩阵,即可去除掉无关的背景区域 代码 使用连通域分析算法去除图像中的空白部分 并将图像变为统一大小的正方形 from skimage import measure imp…...

SurfaceFlinger的硬件Vsync深入分析-千里马android framework车机手机系统开发
背景: 学过或者你看过surfaceflinger相关文章同学都知道,vsync其实都是由surfaceflinger软件层面进行模拟的,但是软件模拟有可能会有误差或偏差,这个时候就需要有个硬件vsync帮忙校准。 故才会在surfaceflinger的systrace出现如下…...

力扣160. 相交链表
目录 1.解题思路2.代码实现 1.解题思路 首先分析,如果两个链表的长度不一,假设他们有交点,那么他们的最后一定是相同的,也即是后面为相同的部分,但前面不好说,而又因为长度不一又没法简便的一一对比&#…...
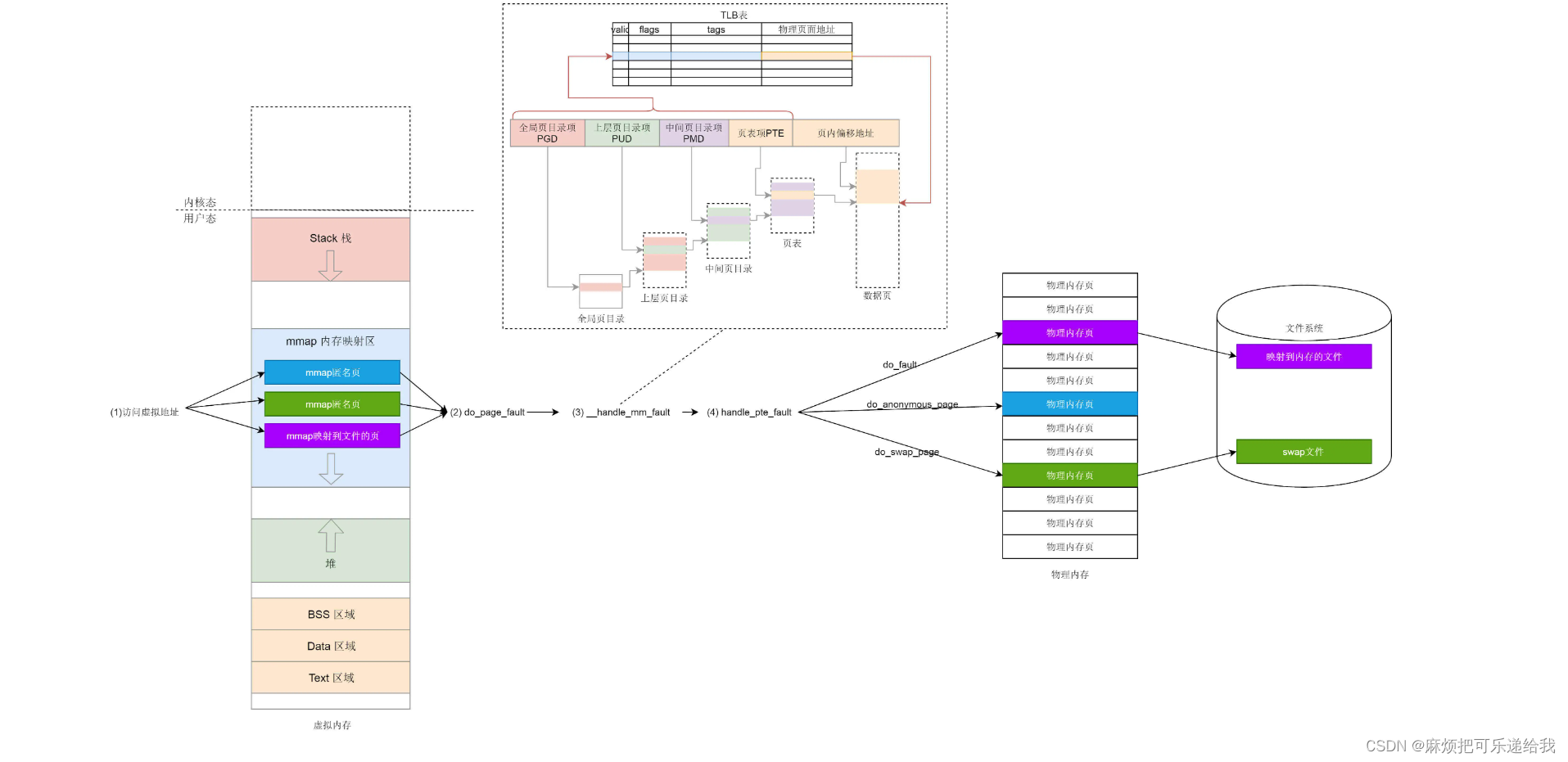
操作系统学习与思考
x86体系架构 x86是因特尔8086代芯片的CPU总线位数以及寄存器种类的规范,大部分操作系统都是以该规范作为基准来生产的 计算机组成 CPU,可以根据程序计数器进行取指令操作,并根据指令执行运算(加、减、乘、除)。运算所…...
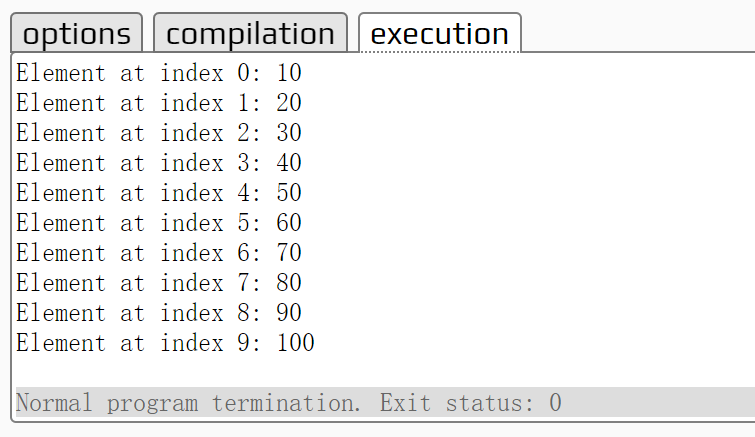
C++笔记之动态数组的申请和手动实现一个简单的vector
C笔记之动态数组的申请和手动实现一个简单的vector code review! 文章目录 C笔记之动态数组的申请和手动实现一个简单的vector1.C语言中动态数组的申请与使用1.动态数组的申请使用new和delete使用std::vector 1.std::vector的底层实现2.手动实现一个简单的vector:使用一个指向…...
答题测评考试小程序的效果如何
在线答题系统是一种在线练习、考试、测评的智能答题系统,适用于企业培训、测评考试、知识竞赛、模拟考试等场景,管理员可任意组题、随机出题,答题者成功提交后,系统自动判分。 多种题目类型,两种答题模式 练习模式&a…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

