刷题记录:牛客NC23054华华开始学信息学 线段树+分块
传送门:牛客
题目描述:
题目latex公式较多,此处省略
输入:
10 6
1 1 1
2 4 6
1 3 2
2 5 7
1 6 10
2 1 10
输出:
3
5
26
这道题让我体验到的线段树相对于树状数组的常数巨大
我们倘若直接用单点修改的话,如果D过小比如1那么我们足足要加n次,时间复杂度爆炸。
那如果我们把每次要相加的记录下来lazy[D]+=K那么在我们计算和时
for (int i=1;i<=n;i++)ans+=(b/i - (a-1)/i)*lazy[i]
我们发现我们同样复杂度无法接受
所以对于本题来说,我们需要有一个分块的想法,也就是找一个界限,在界限的两边采用不同的算法,使得我们的总体复杂度可以接受.我们设这个度为S.我们发现我们的模数越大,显然对直接暴力修改时越有利的,因为我们需要修改的点就越小.反之我们应选用记录lazy的方式
那么对于第一种方法来说,我们的最坏复杂度为n/S∗logn∗mn/S*logn*mn/S∗logn∗m
对于第二种方法来说,我们的最坏复杂度为S∗mS*mS∗m
我们的总体复杂度为n/S∗logn∗m+S∗mn/S*logn*m+S*mn/S∗logn∗m+S∗m(实际上应该是小于这个值的,因为操作总数为m,此时为了方便,我们将两种方法都当做m)
此时显然运用均值不等式的小知识,我们会发现当SSS=n∗logn\sqrt{n*logn}n∗logn时取到最小值,此时我们的复杂度大概为1e81e81e8左右
此时我就要吐槽了,牛客上对于这道题,几乎所有的解法(包括题解),都是直接取用SSS=n\sqrt{n}n,此时的复杂度应该是m∗n∗lognm*\sqrt{n}*lognm∗n∗logn,达到了1e9多了,然而他们使用树状数组是可以直接过的(还跑的飞快).嗯,我可以理解,毕竟时限开到了2s2s2s,牛客跑的快,可能仍然可以跑过去.但是我TM使用线段树就被卡了,我直接想大骂,难道就没人尊重线段树爱好者吗(虽然线段树常数确实较大),想用线段树的话必须要用上述的最优的分界点S
并且因为直接计算n∗logn\sqrt{n*logn}n∗logn速度较慢所以我们不能把这个式子放在循环里,这样依旧会Tle,所以我们需要提前计算出这个值(当时我还以为这道题卡定线段树了呢,即使用了最优分界点仍然过不去…)
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r,sum;
}tree[maxn*4];
int n,m;
void pushup(int rt) {tree[rt].sum=tree[ls].sum+tree[rs].sum;
}
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;if(l==r) return ;int mid=(l+r)>>1;build(lson);build(rson);
}
void update(int pos,int v,int rt) {if(tree[rt].l==pos&&tree[rt].r==pos) {tree[rt].sum+=v;return ;}int mid=(tree[rt].l+tree[rt].r)>>1;if(pos<=mid) update(pos,v,ls);else update(pos,v,rs);pushup(rt);
}
int query(int l,int r,int rt) {if(tree[rt].l==l&&tree[rt].r==r) {return tree[rt].sum;}int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid) return query(l,r,ls);else if(l>mid) return query(l,r,rs);else return query(l,mid,ls)+query(mid+1,r,rs);
}
int Add[maxn];
signed main() {n=read();m=read();build(root);double sq=sqrt((double)n*log((double)n));for(int i=1;i<=m;i++) {int opt=read();if(opt==1) {int d=read(),k=read();if(d>sq) {
// cout<<d<<" "<<sqrt((double)n*log((double)n))<<endl;for(int i=d;i<=n;i+=d) {update(i,k,1);}}else {Add[d]+=k;}}else {int l=read(),r=read();int ans=query(l,r,1);for(int i=1;i<=sq;i++){ans+=Add[i]*(r/i-(l-1)/i);}printf("%lld\n",ans);}}return 0;
}
相关文章:

刷题记录:牛客NC23054华华开始学信息学 线段树+分块
传送门:牛客 题目描述: 题目latex公式较多,此处省略 输入: 10 6 1 1 1 2 4 6 1 3 2 2 5 7 1 6 10 2 1 10 输出: 3 5 26这道题让我体验到的线段树相对于树状数组的常数巨大 我们倘若直接用单点修改的话,如果D过小比如1那么我们足足要加n次,时间复杂度爆…...

二叉搜索树(查找,插入,删除)
目录 1.概念 2.性质 3.二叉搜索树的操作 1.查找 2.插入 3.删除(难点) 1.概念 二叉搜索树又称二叉排序树.利用中序遍历它就是一个有顺序的一组数. 2.性质 1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 2.若它的右子树不为空,则右子树上所有节点的值都…...

C# PictureEdit 加载图片
方法一: 如果要加载的图片的长宽比不是太过失衡, 1.可以改变picturebox的SizeMode属性为 PictureBoxSizeMode.StretchImage, 2.或者Dev控件 PictureEdit的SizeMode属性为Zoom。(zoom:缩放;clip剪短;stret…...
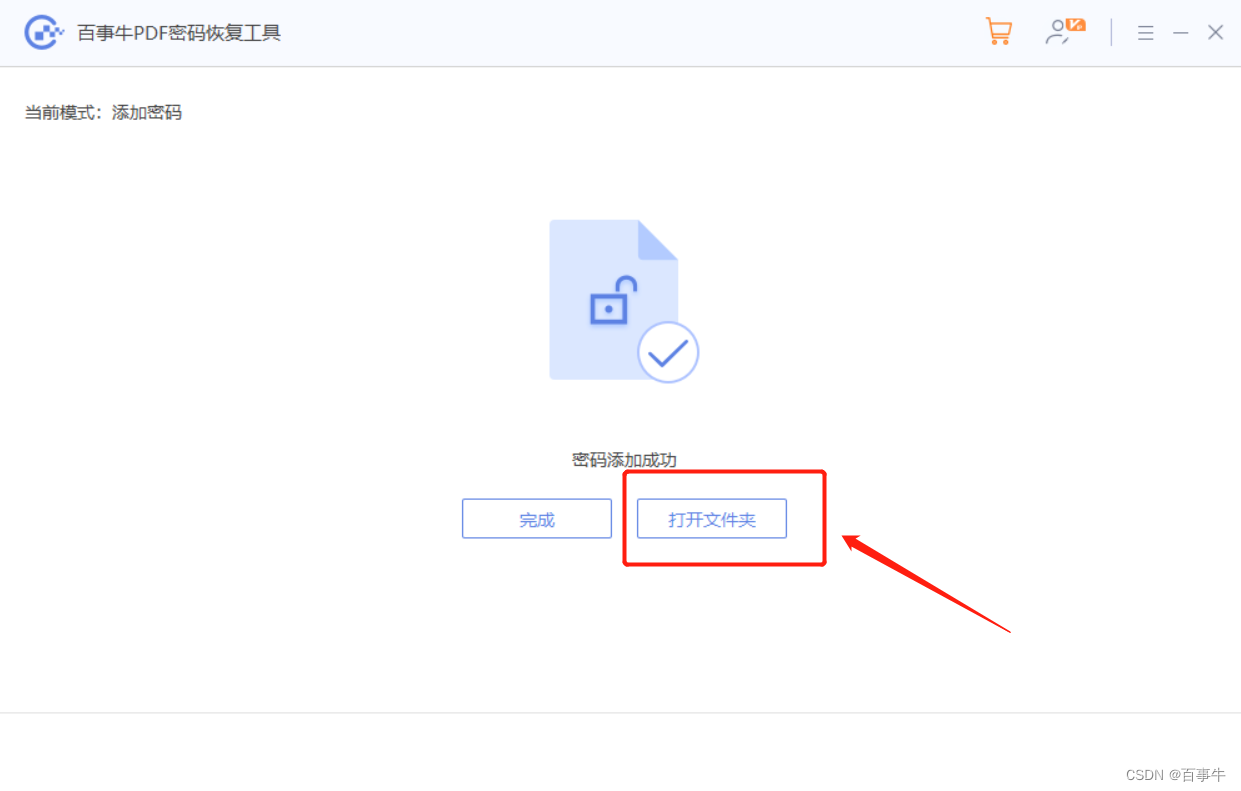
3种方法设置PDF“打开密码”,总有一种适合你
PDF文件是我们工作中经常用到的文件之一,对于重要的文件,设置“打开密码”是一种很好的保护方式。下面就来说说,设置PDF“打开密码”有哪三种方法? 方法一:在线网站加密 市面上有很多可以直接在线上加密PDF文件的产品…...
-计算机网络(笔记))
第三章 数据链路层(点到点的传输服务)-计算机网络(笔记)
计算机网络 第三章 数据链路层(点到点的传输服务) 数据链路层属于计算机网络的低层。数据链路层使用的信道主要有以下两种类型: (1)点到点信道。这种信道使用一对一的点到点通信方式。 (2)广…...

volatile关键字与CAS机制
volatile关键字 volatile关键字可以对类的成员变量与静态变量进行修饰 volatile关键字的作用 1.保证被修饰属性的可见性,被修饰后的属性如果被更改后其他线程是会立即可见的 2.保证被修饰属性的有序性,被修饰后的属性禁止修改指令执行的顺序 注意:volatile关键字不能保证属性…...

LeetCode题解 动态规划(四):416 分割等和子集;1049 最后一块石头的重量 II
背包问题 下图将背包问题做了分类 其中之重点,是01背包,即一堆物件选哪样不选哪样放入背包里。难度在于,以前的状态转移,多只用考虑一个变量,比如爬楼梯的阶层,路径点的选择,这也是能用滚动数组…...

【FFMPEG源码分析】从ffplay源码摸清ffmpeg框架(二)
demux模块 从前面一篇文章中可以得知,demux模块的使用方法大致如下: 分配AVFormatContext通过avformat_open_input(…)传入AVFormatContext指针和文件路径,启动demux通过av_read_frame(…) 从AVFormatContext中读取demux后的audio/video/subtitle数据包…...
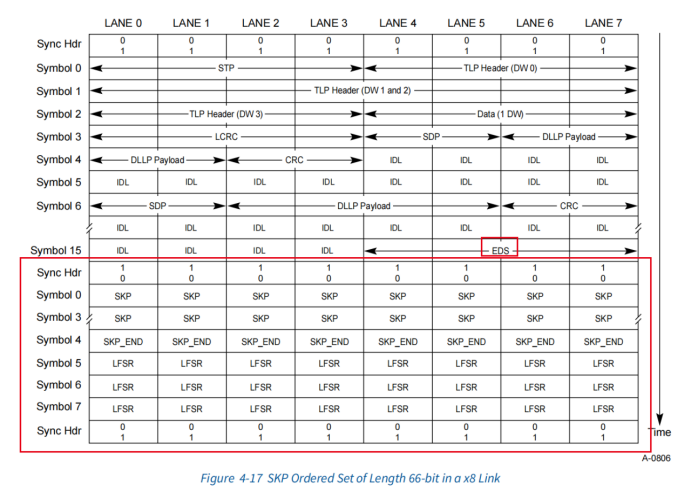
PCIE 学习笔记(入门简介)
PCIE 学习笔记书到用时方恨少啊,一年前学PCIE的笔记,再拿出来瞅瞅。发到博客上,方便看。PCIE基础PCIE和PCI的不同PCIE采用差分信号传输,并且是dual-simplex传输——每条lane上有TX通道和RX通道,所以每条lane上的信号是…...
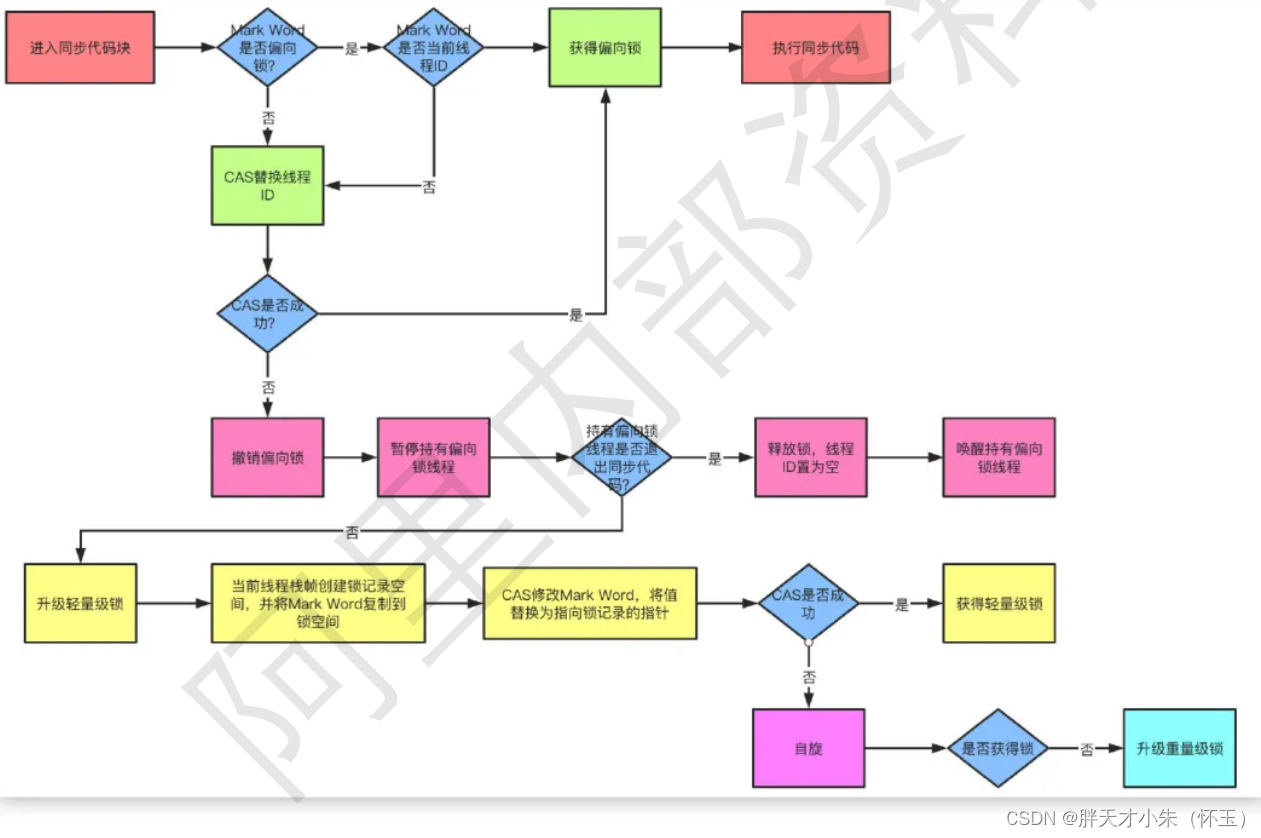
锁的优化机制了解嘛?请进!
点个关注,必回关 文章目录自旋锁:自适应锁:锁消除:锁粗化:偏向锁:轻量级锁:从JDK1.6版本之后,synchronized本身也在不断优化锁的机制,有些情况下他并不会是一个很重量级的…...

5.点赞功能 Redis
Redis(1)简介Redis 是一个高性能的 key-value 数据库原子 – Redis的所有操作都是原子性的。多个操作也支持事务,即原子性,通过MULTI和EXEC指令包起来。非关系形数据库数据全部存在内存中,性能高。(2&#…...
)
Java序列化和反序列化(详解)
一、理解Java序列化和反序列化 Serialization(序列化):将java对象以一连串的字节保存在磁盘文件中的过程,也可以说是保存java对象状态的过程。序列化可以将数据永久保存在磁盘上(通常保存在文件中)。 deserialization(反序列化):将保存在磁…...

【刷题篇】链表(上)
前言🌈前段时间我们学习了单向链表和双向链表,本期将带来3道与链表相关的OJ题来巩固对链表的理解。话不多说,让我们进入今天的题目吧!🚀本期的题目有:反转单链表、链表的中间结点、合并两个有序链表反转单链…...

ConcurrentHashMap设计思路
ConcurrentHashMap设计思路Hashtable vs ConcurrentHashMapHashtable vs ConcurrentHashMap Hashtable 对比 ConcurrentHashMap Hashtable 与 ConcurrentHashMap 都是线程安全的 Map 集合Hashtable 并发度低,整个 Hashtable 对应一把锁,同一时刻&#…...

Unity基于GraphView的行为树编辑器
这里写自定义目录标题概述基于GitHub上:目前这只是做了一些比较基础的功能节点开发,仅仅用于学习交流,非完成品。项目GitHub连接:[https://github.com/HengyuanLee/BehaviorTreeExamples](https://github.com/HengyuanLee/Behavio…...
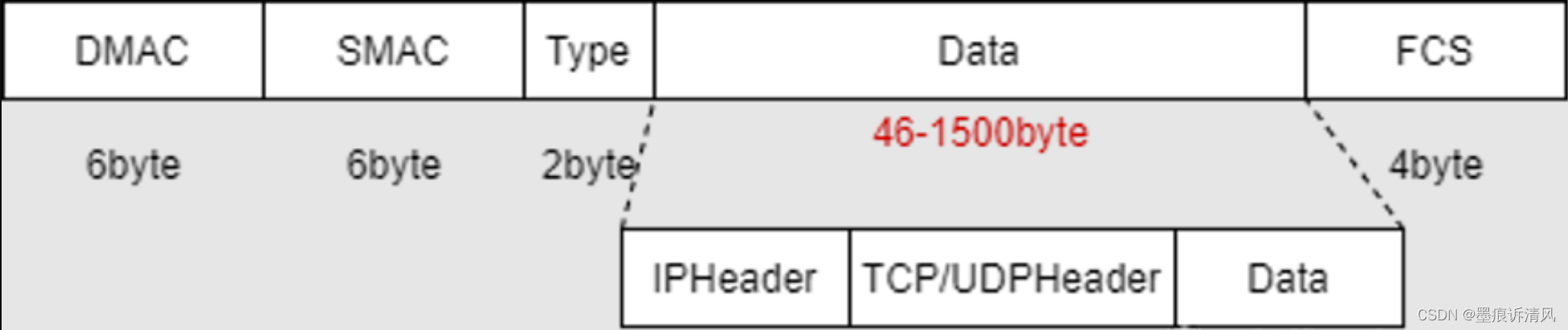
网络流量传输MTU解析
基本概念 以太网的链路层对数据帧的长度会有一个限制,其最大值默认是1500字节,链路层的这个特性称为MTU,即最大传输单元 Maximum Transmission Unit,最大传输单元,指的是数据链路层的最大payload,由硬件网…...
)
30个HTML+CSS前端开发案例(四)
30个HTMLCSS前端开发案例(17-20)鼠标移入文字加载动画效果代码实现效果鼠标悬停缩放效果实现代码效果鼠标移入旋转动画实现代码效果loding加载动画实现代码效果资源包鼠标移入文字加载动画效果 代码实现 <!DOCTYPE html> <html><head&g…...

《TPM原理及应用指南》学习 —— TPM执行环境3
本文对应《A Practical Guide to TPM 2.0 — Using the Trusted Platform Module in the New Age of Security》的第6章第3节。 6.3 Summary —— 总结 Now that you have an execution environment (or maybe both of them) set up, you’re ready to run the code samples f…...
实验名称:经典同步问题:生成者与消费者问题
实验名称:经典同步问题:生成者与消费者问题 相关知识 信号量 信号量是用来协调不同进程间的数据对象,可用来保护共享资源,也能用来实现进程间及同一进程不同线程间的进程同步。分为二值信号灯和计算信号灯两种类型。 进程与线…...

EasyCVR视频云存储的架构解析与Sharelist云存挂载方法介绍
一、什么是视频云存储? 视频云存储主要用于为上层应用提供视频文件、结构化信息、事件信息的相关服务。云存储节点分为数据文件存储节点和结构化数据存储节点。数据文件存储节点主要用于视频、图片的存储。结构化数据存储节点用于存储结构化数据并提供相关服务。 …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
