动态规划算法实现0-1背包问题Java语言实现
问题介绍:

动态规划算法:
动态规划(Dynamic Programming)是一种解决多阶段决策问题的优化算法。它通过将问题分解为一系列子问题,并利用子问题的解来构建更大规模问题的解,从而实现对整个问题的求解。
动态规划算法通常适用于满足以下两个条件的问题:
-
重叠子问题(Overlapping Subproblems):原问题可以被分解为一系列相互重叠的子问题,这意味着解决子问题时可能会重复计算相同的子问题。
-
最优子结构(Optimal Substructure):原问题的最优解可以通过子问题的最优解来构建,即全局最优解必然包含局部最优解。
动态规划算法的基本思想是利用一个表格(通常是二维数组)来存储子问题的解,通过填表的方式逐步求解更大规模的问题,直到得到最终的解。在填表的过程中,可以利用已经计算过的子问题的解来避免重复计算。
动态规划算法一般涉及以下步骤:
-
定义状态:确定问题的状态,并设计状态表示方法。
-
确定状态转移方程:根据子问题之间的关系,建立状态转移方程,描述问题的最优解与子问题的最优解之间的关系。
-
初始化:初始化表格中的边界条件,即最简单的子问题的解。
-
递推计算:按照状态转移方程,从小规模子问题开始逐步计算,填充表格中的值,直到计算出原问题的解。
-
求解原问题:根据填充好的表格,得到原问题的最优解。
public class KnapsackProblem {public static int knapsack(int[] weights, int[] values, int capacity) {int n = weights.length;int[][] dp = new int[n + 1][capacity + 1];// 初始化第一行和第一列为0for (int i = 0; i <= n; i++) {dp[i][0] = 0;}for (int j = 0; j <= capacity; j++) {dp[0][j] = 0;}// 动态规划求解for (int i = 1; i <= n; i++) {for (int j = 1; j <= capacity; j++) {if (weights[i - 1] <= j) {// 当前物品的重量小于等于背包容量,可以选择放入背包dp[i][j] = Math.max(values[i - 1] + dp[i - 1][j - weights[i - 1]], dp[i - 1][j]);} else {// 当前物品的重量大于背包容量,无法放入背包dp[i][j] = dp[i - 1][j];}}}return dp[n][capacity];}public static void main(String[] args) {int[] weights = {2, 3, 4, 5};int[] values = {3, 4, 5, 6};int capacity = 8;int maxTotalValue = knapsack(weights, values, capacity);System.out.println("Maximum total value: " + maxTotalValue);}
}
相关文章:

动态规划算法实现0-1背包问题Java语言实现
问题介绍: 动态规划算法: 动态规划(Dynamic Programming)是一种解决多阶段决策问题的优化算法。它通过将问题分解为一系列子问题,并利用子问题的解来构建更大规模问题的解,从而实现对整个问题的求解。 动态…...

linux查看系统版本
linux主机 hostnamectl -- 可以查看 “系统架构”,“发行版本”和“内核版本”等信息 uname -a -- 查看内核版本 cat /proc/version -- 查看当前操作系统版本信息 cat /etc/issue ,lsb_release -a(ubuntu)-- 查看…...
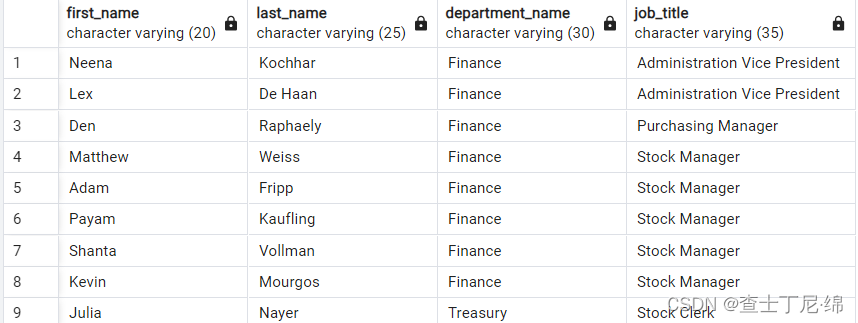
pg14-sql基础(四)-多表联查
多表联查 内联查询 SELECT e.department_id, e.first_name, d.department_name FROM employees e INNER JOIN departments d -- JOIN departments d ON e.department_id d.department_id;左外联查询 SELECT e.department_id, e.first_name, d.department_name FROM employees…...

el-date-picker 日期时间选择器 限时时间范围 精确到时分秒
官方的disabledDate属性:设置禁用状态,参数为当前日期,要求返回 Boolean,它只能禁用日期,对于时间并不能直接禁用,总结以下两个方法解决禁用时间: 1.通过watch去监听源数据: 1.1 组…...
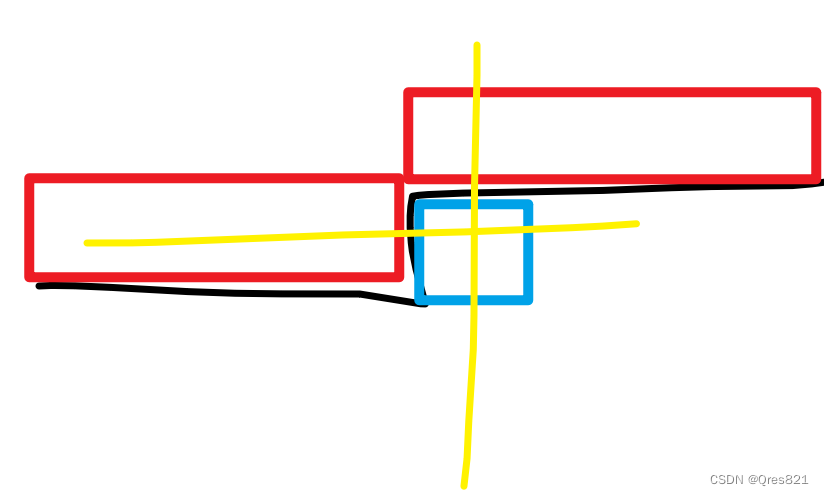
轮廓线dp:GYM103446C
https://vjudge.net/contest/591700#problem/H 考虑轮廓线dp,当我们枚举到蓝色格子的时候,我们记录红色格子的状态 每个格子有4种状态 0有向下1需要向上2不用管3需向右 每次枚举的时候,我们需要考虑这个格子的三种状态: 10不放…...

羊驼免疫制备纳米抗体
纳米抗体(nanobodies,Nbs)是由比利时科学家Hamers等人在骆驼血液内首次发现的一种新型抗体,与传统抗体相比,这种抗体不存在轻链,只有重链抗体(HcAb)和两个常规的CH2和CH3区组成&…...

【AI好好玩02】利用Lama Cleaner本地实现AIGC试玩:擦除对象、替换对象、更换风格等等
目录 一、安装二、擦除功能1. LaMa模型实操实例一:去除路人实操实例二:去水印实操实例三:老照片修复 2. LDM模型3. ZITS模型4. MAT模型5. FcF模型6. Manga模型 三、替换对象功能1. sd1.52. sd23. anything44. realisticVision1.45. 四个模型的…...
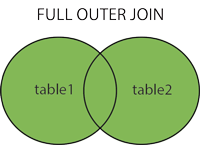
SQL FULL OUTER JOIN 关键字(完整外部连接)||SQL自连接 Self JOIN
SQL FULL OUTER JOIN 关键字 当左(表1)或右(表2)表记录匹配时,FULL OUTER JOIN关键字将返回所有记录。 注意: FULL OUTER JOIN可能会返回非常大的结果集! SQL FULL OUTER JOIN 语法 SELECT …...

专科医院污水处理设备构造解析及工艺流程
诸城市鑫淼环保小编带大家了解一下专科医院污水处理设备构造解析及工艺流程 主要组成部分: 1.预处理单元 处理流程的起点是预处理单元,用于去除废水中的大颗粒物质和固体废物。这一阶段通常包括隔栅和筛网,以确保进一步处理的污水清洁。 2.生…...

【RabbitMQ】RabbitMQ 消息的可靠性 —— 生产者和消费者消息的确认,消息的持久化以及消费失败的重试机制
文章目录 前言:消息的可靠性问题一、生产者消息的确认1.1 生产者确认机制1.2 实现生产者消息的确认1.3 验证生产者消息的确认 二、消息的持久化2.1 演示消息的丢失2.2 声明持久化的交换机和队列2.3 发送持久化的消息 三、消费者消息的确认3.1 配置消费者消息确认3.2…...

百万套行泊一体量产定点,中国市场「开启」智驾高低速集成
进入2023年,席卷中国市场的行泊一体概念方案进入定点、量产交付的第一波高峰期。这套方案,以高性价比、硬件复用、高低速智驾集成的模式,备受市场青睐。 本周,纵目科技宣布,Amphiman3000行泊一体产品获得长安汽车旗下…...
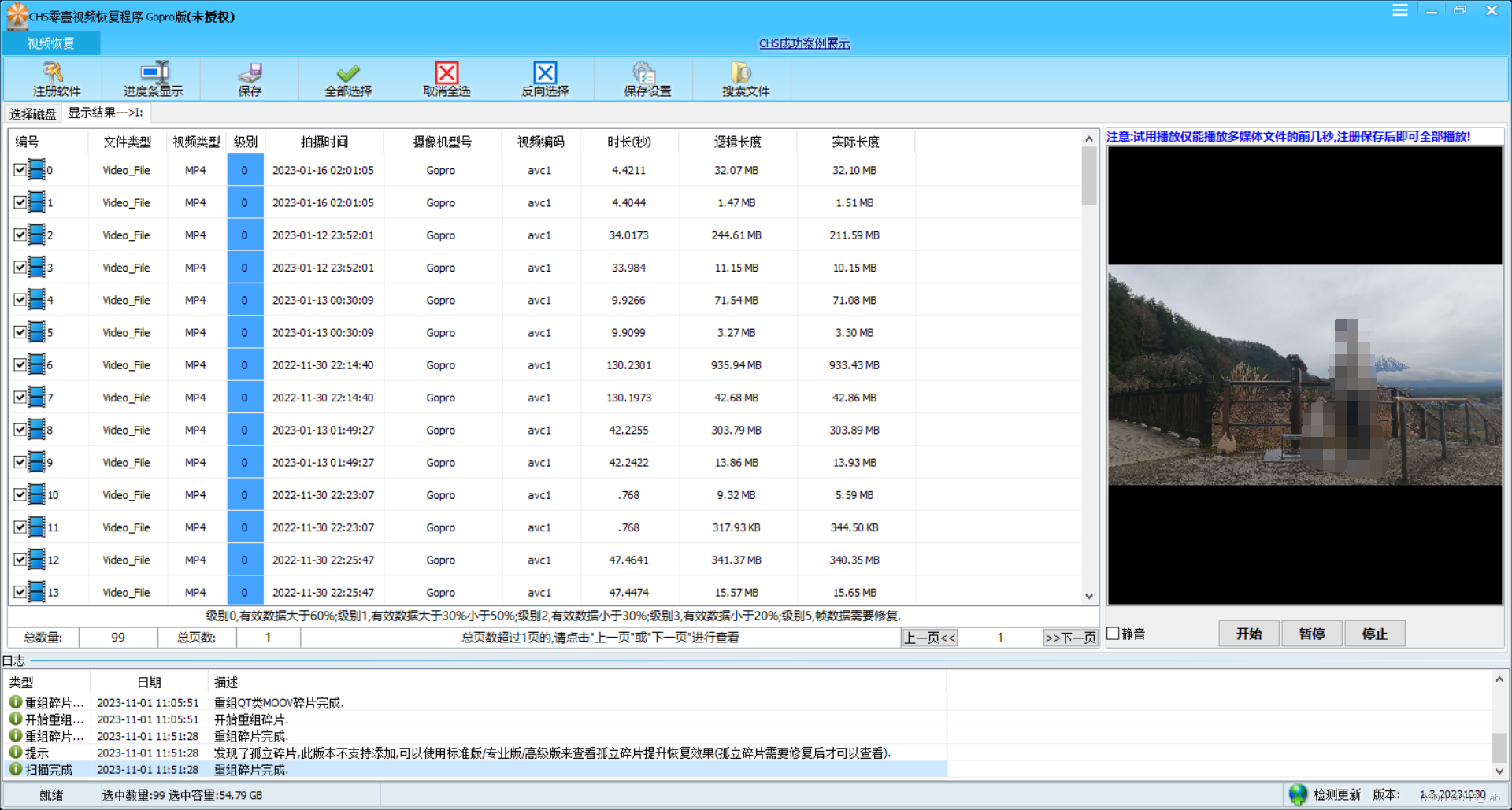
Gopro hero5运动相机格式化后恢复案例
Gopro运动相机以稳定著称,旗下的Hero系列销售全球。下面我们来看一个Hero5格式化后拍了少量素材的恢复案例。 故障存储:64G MicroSD卡 Exfat文件系统 故障现象: 64G的卡没备份数据时做了格式化操作又拍了一条,发现数据没有备份,客户自行使…...

Microsoft Dynamics 365 CE 扩展定制 - 6. 增强代码
在本章中,我们将介绍以下内容: 使用三层模式重构插件用QueryExpressions替换LINQ数据访问层记录自定义项中的错误将插件转换为自定义工作流活动单元测试插件业务逻辑使用内存上下文对插件进行单元测试端到端集成测试插件分析插件构建通用读取审核插件利用CRM Online实现跨来源…...

基于libopenh264 codec的svc分层流实现方案
OpenH264 http://www.openh264.org/ 是标准的H.264 encoder/decoder. ffmpeg已经集成libopenh264,但不支持svc特性。 openh264 encoder支持svc特性: 1. 时域4层:Temporal scalability up to 4 layers in a dyadic hierarchy 2. 空域4层&#…...

为机器学习算法准备数据(Machine Learning 研习之八)
本文还是同样建立在前两篇的基础之上的! 属性组合实验 希望前面的部分能让您了解探索数据并获得洞察力的几种方法。您发现了一些数据怪癖,您可能希望在将数据提供给机器学习算法之前对其进行清理,并且发现了属性之间有趣的相关性,…...

基于Python OpenCV的金铲铲自动进游戏、D牌...
基于Python OpenCV的金铲铲自动进游戏、D牌... 1. 自动点击进入游戏1.1 环境准备1.2 功能实现2. 自动D牌3. 游戏结束自动退1. 自动点击进入游戏 PS: 本测试只用于交流学习OpenCV的相关知识,不能用于商业用途,后果自负。 1.1 环境准备 需要金铲铲在win10的模拟器,我们这里选…...

c++中httplib使用
httplib文件链接:百度网盘 请输入提取码 提取码:kgnq json解析库:百度网盘 请输入提取码 提取码:oug0 一、获取token 打开postman, 在body这个参数中点击raw,输入用户名和密码 然后需要获取到域名和地址。 c++代码如下: #include "httplib.h" #in…...
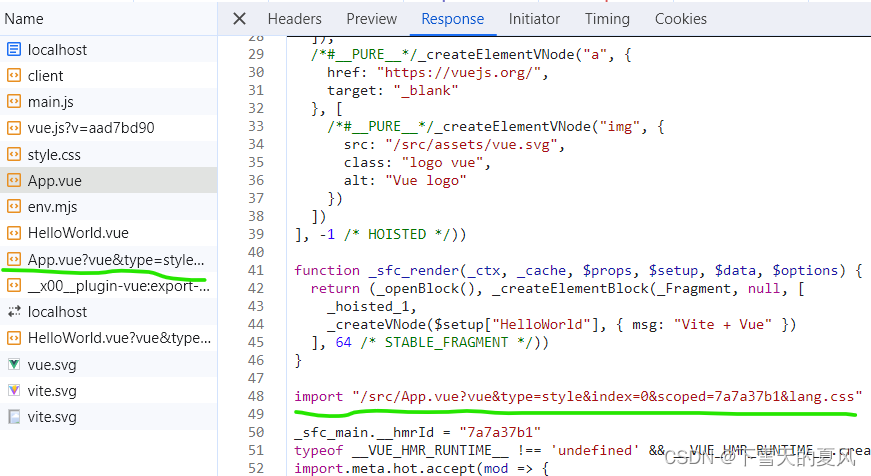
Vite 的基本原理,和 webpack 在开发阶段的比较
目录 1,webpack 的流程2,Vite 的流程简单编译 3,总结 主要对比开发阶段。 1,webpack 的流程 开发阶段大致流程:指定一个入口文件,对相关的模块(js css img 等)先进行打包࿰…...
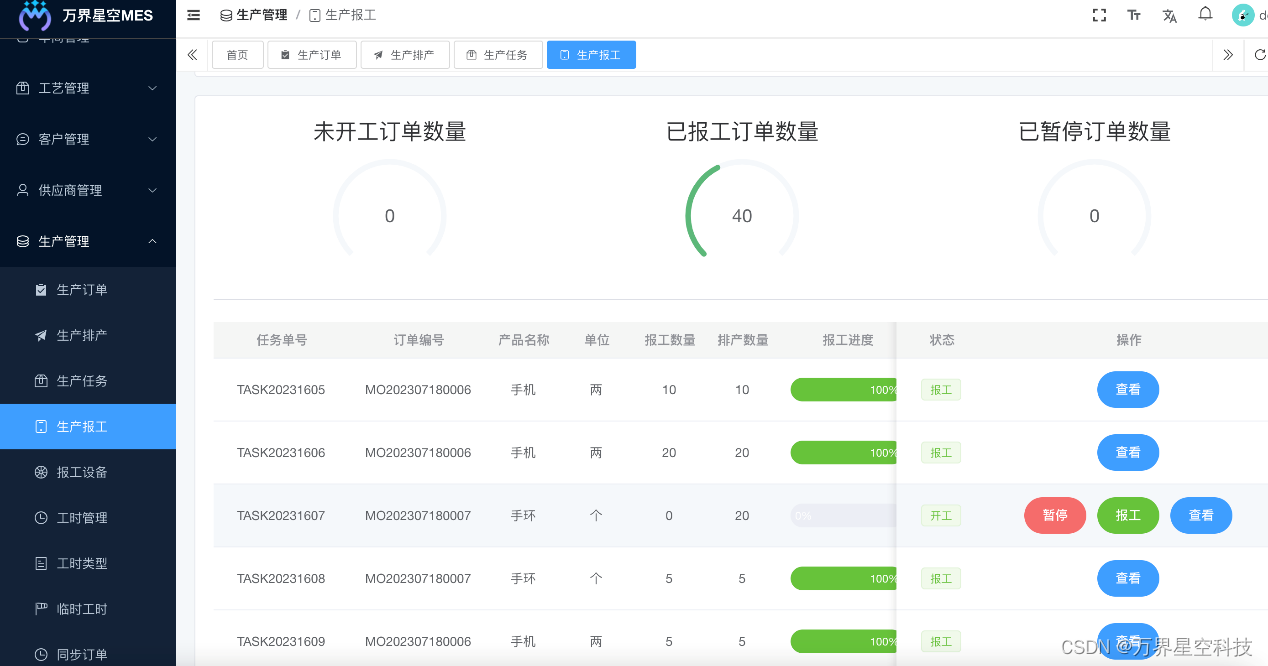
[开源]免费开源MES系统/可视化数字大屏/自动排班系统
开源系统概述: 万界星空科技免费MES、开源MES、商业开源MES、市面上最好的开源MES、MES源代码、免费MES、免费智能制造系统、免费排产系统、免费排班系统、免费质检系统、免费生产计划系统。 万界星空开源MES制造执行系统的Java开源版本。开源mes系统包括系统管理…...

python如何使用gspread读取google在线excel数据?
一、背景 公司使用google在线excel管理测试用例,为了方便把手工测试用到的测试数据用来做自动化用例测试数据,所以就想使用python读取在线excel数据,通过数据驱动方式,完成自动化回归测试,提升手动复制,粘…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
