c语言经典算法—二分查找,冒泡,选择,插入,归并,快排,堆排
一、二分查找
1、前提条件:数据有序,随机访问;
2、实现:递归实现,非递归实现
3、注意事项:
循环退出条件:low <=high,low = high.说明还有一个元素,该元素还要与key进行比较
mid的取值:mid=(low + high)/2;mid = low + ((high - low)>>1)
low 和high 的更新:low = mid +1;high = mid - 1;不能写成low = mid +1,high = mid-1;又可能出现死循环;
代码实现:


1、查找第一个与key相等的元素:
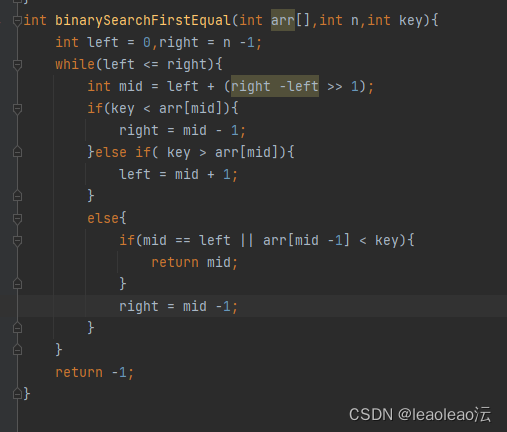
2、查找最后一个与key相等的元素

3、查找最后一个小于等于key值的元素
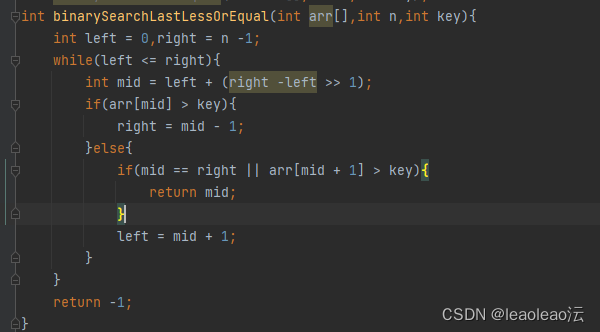
4、查找第一个大于等于key值的元素
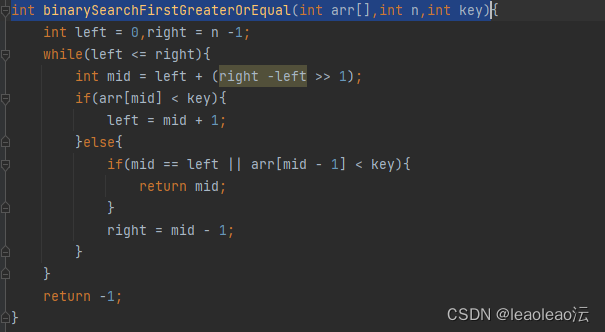
二、冒泡排序
如何评价一个算法:
1、时间复杂度:最好情况;最坏情况;平均情况;系数和低阶项
2、空间复杂度:原地排序(特指空间复杂度为O(1))的排序;
3、稳定性:数据集中“相等”的元素,如果排序前和排序后的相对次序不变,那么这个排序就是稳定的;
稳定性就是排序算法的很重要的指标;
冒泡排序:
比较相邻的元素,如果前一个比后一个大,就交换次序,
对每一对相邻元素做同样的工作,从第一对到最后一对。最大的元素就会位于最后位置;
除最后一个元素外,对其他元素重复上面的步骤,直到元素的个数为1;
时间复杂度:
最好情况原数组有序(O(n));
最坏情况原数组逆序(比较次数(n-1)+(n-2)+...+1 = (n(n-1))/2)
交换次数:((n-1)+(n-2)+...+1 = (n(n-1))/2)
平均情况(每一种情况出现的情况是相等的):总情况(N!)
(比较次数:大于交换的次数,小于(n(n-1))/2)
(交换次数(n(n-1)/4))

分析:有序元素对,逆序元素对,逆序度,有序度;


有序对:34,24,14
逆序对:12,13,23
排序的过程:增加有序度,减少逆序度,最终达到满有序度;
冒泡排序交换导致有序度+1,逆序度-1;
空间复杂度:O(1);//原地排序
稳定性:稳定,arr[j]>arr[j+1] 才发生交换;

三、选择排序(无论什么数据进去都是(O(n2))的时间复杂度,所以用它的时候数据规模越小越好,唯一好处是不占用额外内存)
工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后再从剩余未排序中继续寻找最小(大)元素,然后放到已排序序列的末尾,以此类推,直到所有元素均排序完毕;(选择排序不能像冒泡排序一样去优化)
时间复杂度:O(n2)
比较次数:(n-1)+ ...+1 =(n(n-1))/2
交换次数:n-1;
空间复杂度:O(1)原地排序
稳定性:不稳定,发生了长距离的交换;

四、插入排序:
工作原理:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在从后向前扫描过程中,需要反复把已排序的元素逐步向后挪位,为最新元素提供插入空间;
时间复杂度:
最好情况:(O(n))
原数组有序(比较次数,(n-1))交换次数:原数组有序(0)
最坏情况:(O(n2))
原数组逆序(比较次数,(n-1)+(n-2)+...+1 = (n(n-1))/2);
交换次数((n-1)+(n-2)+...+1 =(n(n-1))/2:
平均情况:
比较次数:大于交换次数,小于(n(n-1))/2
交换次数:(n(n-1))/4(逆序个数)
插入排序好处,当元素基本有序时,其性能非常好;
空间复杂度,O(1),原地排序
稳定性:稳定;

冒泡排序,选择排序,插入排序小结:
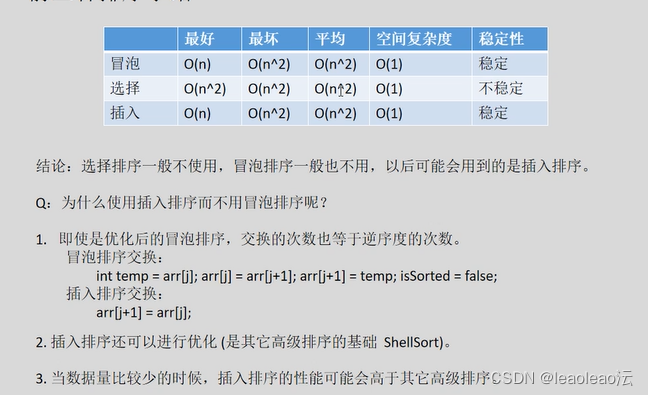
五、希尔排序(缩小增量排序,插入排序的改进版本):
第一批打破O(n2)这个时间复杂度的方法;
gap(希尔):n/2、n/4、...1;
gap = n/2=5

先按gap分组,组内使用简单的插入排序(十个元素分为5组);

第一次组间排序完成后,就缩小增量,gap=5/2=2;gap =1;
时间复杂度比O(n2)小,和具体的gap序列相关;
空间复杂度O(1)原地排序;
稳定性:不稳定,会发生长距离交换;

六、归并排序:
先把大数组分成两个小数组,直到有序再合并;单个数组已经算是有序的;
用递归解决;
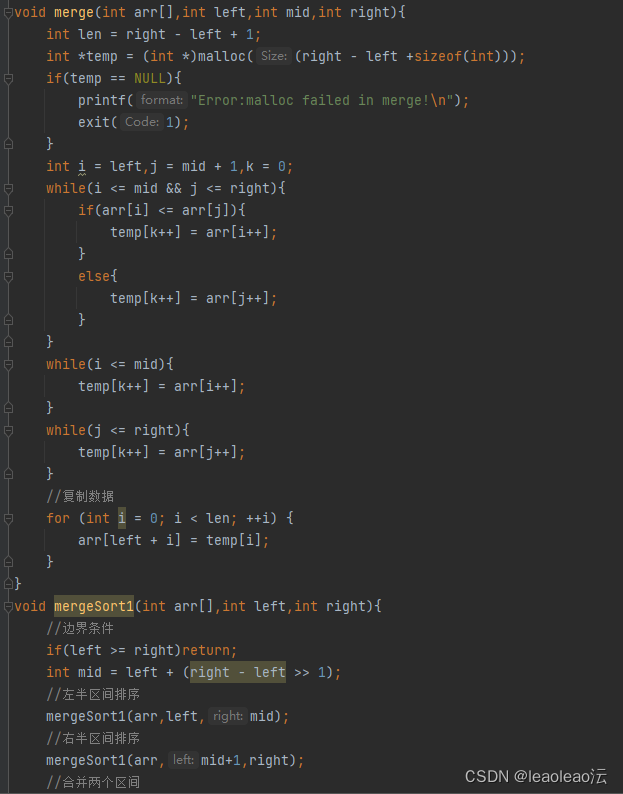
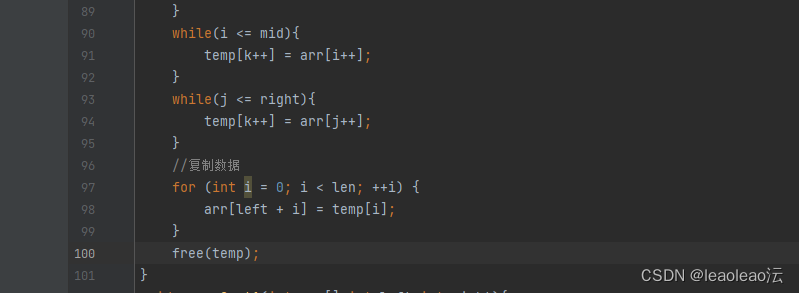
注意释放堆区数组
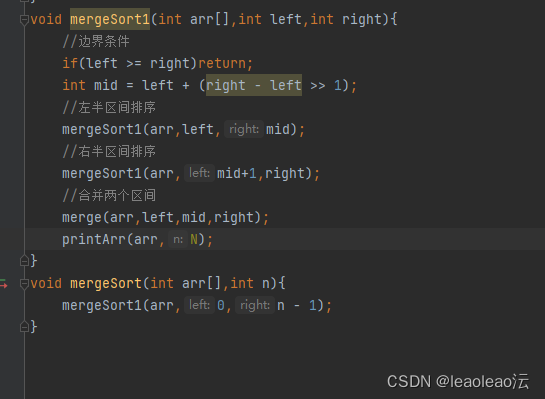


七、快速排序
从数列中挑出一个元素,称为“基准”(pivot);(一般情况下可以选几个值取中位数,也可以选第一位,或者随机位)
重新排序数列,所有元素比基准值小的拜访在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任意边。)在这个分区退出后,改基准就处于数列的中间位置(也就是最终位置)这个操作我们称之为分区(partition);
递归地把小于基准值元素地子数列和大于基准值元素地子数列排序(左右两边都使用快排);

i 是放下一个比基准值小的位置,j放比基准值大的值;先移动 j 再移动 i ;
先找比基准值小的,再找比基准值大的,交替找直到 i j 相遇,基准值的位置就确定了;
因为基准值已经保存就可以移动 j 把第一个值覆盖掉(以第一个值为基准)

时间复杂度:
最好情况:(每次分区都分成大小相等的两份)![]()

最坏情况:每次基准值都位于最左边或者最右边;
![]()

平均情况(假设每次分成三比一的情况):
![]()

空间复杂度:![]()


快速排序的改进策略(基准值的选取(随机选,选择多个元素的中位数);分区操作的优化;选择多个基准值);
八、堆排序
二叉堆(大顶堆(根节点的键大于左右子树所有结点的键,并且左右子树都是大顶堆);小顶堆(根节点的键小于左右子树所有结点的键,并且左右子树都是小顶堆))

把数组看作一个完全二叉树;

堆排算法:
把完全二叉树构建成大顶堆,找到第一个非叶子结点,从后往前构建大顶堆
把堆顶元素和无序区的最后一个元素交换,交换之后无序区的长度减一,
把无序区重新调整成大顶堆,重复上一步操作,直到无序区的长度为1;


归并(缺点:占用内存空间复杂度O(n)),快排,堆排
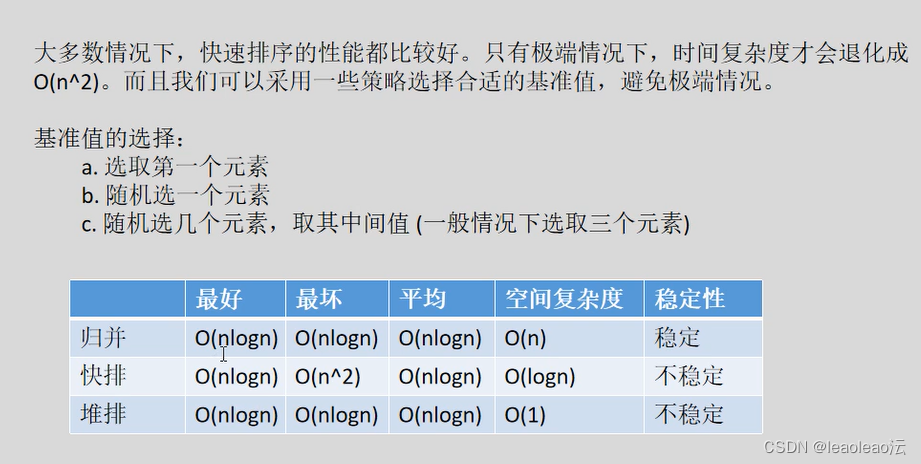
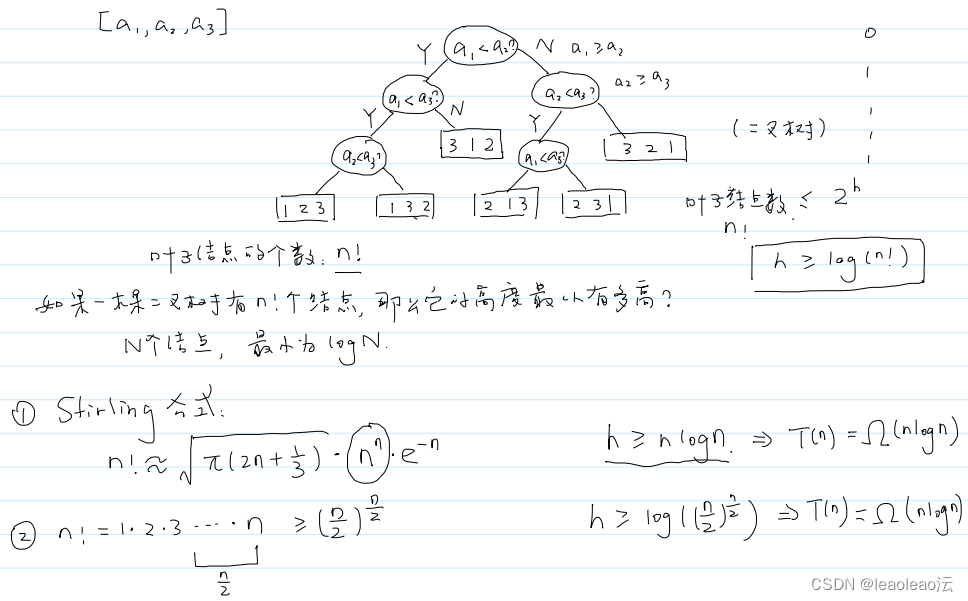
九、基于比较的排序算法
证明:基于比较 的排序算法,时间复杂度的下限就是O(nlogn);
相关文章:

c语言经典算法—二分查找,冒泡,选择,插入,归并,快排,堆排
一、二分查找 1、前提条件:数据有序,随机访问; 2、实现:递归实现,非递归实现 3、注意事项: 循环退出条件:low <high,low high.说明还有一个元素,该元素还要与key进行比较 mid的取值…...
网站SSL证书有什么用
在当今,网站安全对于企业和个人来说至关重要。其中,SSL证书在保护网站和用户数据方面发挥着关键作用。 1,数据加密保护:SSL证书通过使用加密技术,将网站与访问者之间的通信进行加密。这意味着通过SSL保护的网站上的数据…...
ubuntu 20.04 server安装
ubuntu 20.04 server安装 ubuntu-20.04.6-live-server-amd64.iso 安装 安装ubuntu20.04 TLS系统后,开机卡在“A start job is running for wait for network to be Configured”等待连接两分多钟。 cd /etc/systemd/system/network-online.target.wants/在[Servi…...

造数工具调研
开源项目 语言 地址 描述 备注 Faker Python https://github.com/joke2k/faker 一个Python库,可以生成各种各样的假数据,包括SQL语句。它支持多种数据库,包括MySQL、PostgreSQL、Oracle等。Faker可以生成各种类型的数据,如…...
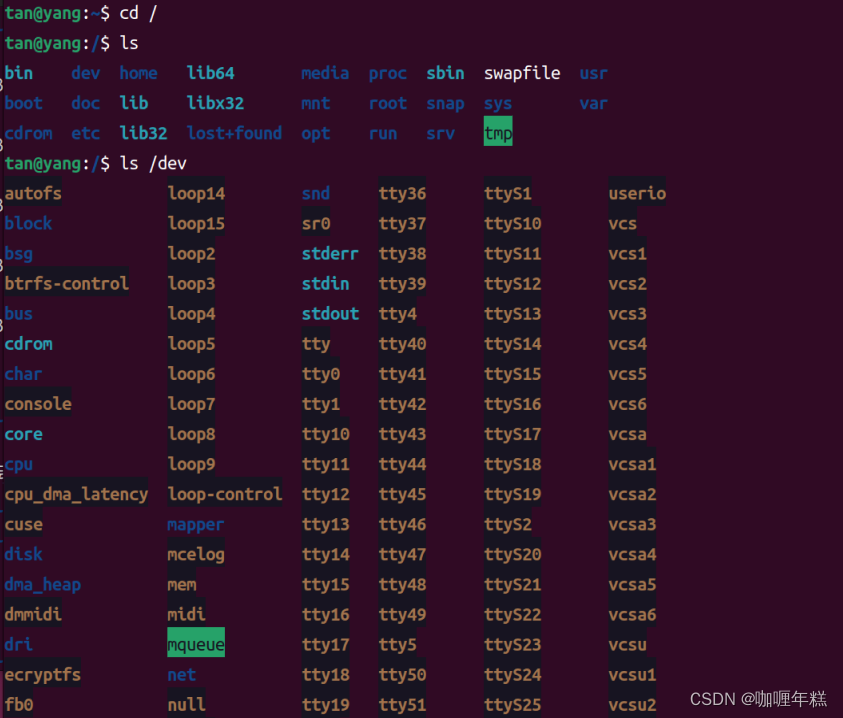
Linux文件系统目录结构
典型的Linux文件系统目录结构的列表 典型的Linux文件系统目录结构的列表。每个目录都有其特定的用途: /bin: 存放系统引导和修复所需的二进制可执行文件,如ls,cp,mv等命令。 /boot: 存放操作系统引导文件,例如内核和…...

CANoe新建XML自动化Test Modules
文章目录 1.打开Test Modules2.新建Environment3.新建XML Test Modules4.新建.can文件5.打开XML Test Modules6.新建xml脚本并保存7.编译8.在.can文件写个测试用例9.修改报告格式为HTML10.运行查看报告后面介绍的文章会重复用到这部分,这里单独介绍下,后面不做重复介绍。 1.…...

国内某发动机制造工厂RFID智能制造应用解决方案
一、工厂布局和装备 国内某发动机制造工厂的装配车间布局合理,设备先进,在这个5万平方米的生产区域内,各个工位之间流程紧密,工厂采用了柔性设备,占比达到了67%,数控化率超过90%,自动化率达到了…...
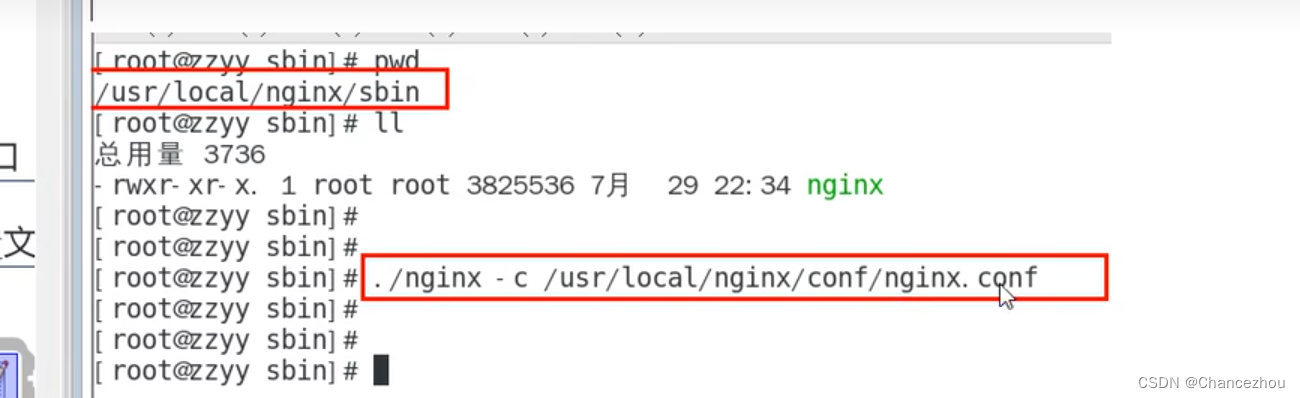
【SpringCloud Alibaba -- Nacos】Linux 搭建 Nacos 集群
搭建 Nacos 集群 架构 centos安装docker https://docs.docker.com/engine/install/centos/ 详细配置过程 MySql8 mysql数据库配置 数据库脚本 nacos/conf/nacos-mysql.sql Nacos2 application.properties 修改为mysql spring.datasource.platformmysqldb.num1 db.url…...

程序员使用 ChatGPT的 10 种最佳方式
自2022年11月30日发布以来,ChatGPT持续爆火,它在各个方面都产生了巨大的影响力,在软件开发行业,ChatGPT 有潜力彻底改变我们思考和处理软件开发的方式。 ChatGPT 正在改变软件开发流程,它理解自然语言和生成类人文本的…...

各种各类好用热门API推荐
各种各类的好用API推荐,含免费次数~ 天气预报查询:查询全国以及全球多个城市的天气,包含15天天气预报查询。天气预警:可以获取指定城市当前生效中的各类天气预警,如寒潮蓝色预警信号,或一次性拉取全国所有…...
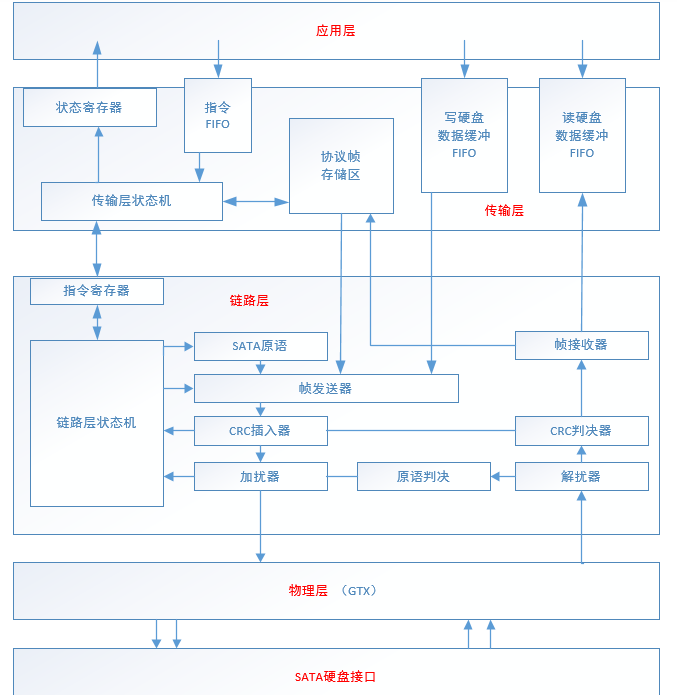
高速串行总线——SATA
SATA简介 SATA的全称是Serial Advanced Technology Attachment(串行高级技术附件,一种基于行业标准的串行硬件驱动器接口),它是一种电脑总线,主要功能是用作主板和大量存储设备(如硬盘及光盘驱动器)之间的数据传输 SA…...
不用流氓软件,如何在户外使用手机听下载到家中电脑里的音乐文件呢?
文章目录 本教程解决的问题是:按照本教程方法操作后,达到的效果是本教程使用环境:1 群晖系统安装audiostation套件2 下载移动端app3 内网穿透,映射至公网 很多老铁想在上班路上听点喜欢的歌或者相声解解闷儿,于是打开手…...

函数数组指针示例
函数数组指针是一个指向函数指针数组的指针。它用于存储一组函数指针,使您可以通过函数指针数组的索引来调用不同的函数。函数数组指针通常用于实现函数表或分发不同的操作或处理不同的事件。 以下是一个简单的示例,说明如何声明和使用函数数组指针&…...

万宾科技管网水位监测预警,管网水位的特点有哪些?
以往如果要了解城市地下排水管网的水位变化,需要依靠人工巡检或者排查的方式,这不仅加大了人员的工作量,而且也为市政府带来了更多的工作难题。比如人员监管监测不到位或无法远程监控等情况,都会降低市政府对排水管网的管理能力&a…...

vue element admin master 去掉登陆
vue element admin master 去掉登陆 修改/src/permission.js import router from ./router import store from ./store import { Message } from element-ui import NProgress from nprogress // progress bar import nprogress/nprogress.css // progress bar style import {…...

没有MES管理系统,先用数据采集设备能有用吗
在当前的数字化时代,企业纷纷意识到了数字化转型的重要性。数据被誉为新型生产要素,对于企业的运营和决策具有至关重要的作用。在数字化转型的过程中,许多企业面临着一个共同的问题:如何获取所需的数据? 有两家企业在…...
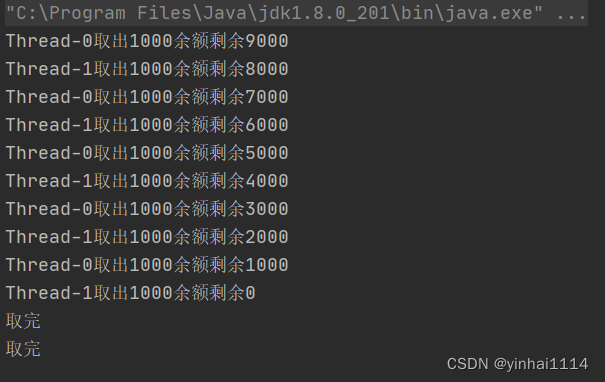
【JAVA学习笔记】61 - 线程入门、常用方法、同步机制,以及本章作业(难点)
项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter17/src/com/yinhai 线程 一、线程相关概念 1.程序 是为完成特定任务、用某种语言编写的一组指令的集合。简单的说:就是我们写的代码 2.进程 1)进程是指运行中的程序&#x…...
)
C#开发的OpenRA游戏之步兵射击(2)
C#开发的OpenRA游戏之步兵射击(2) 前面已经分析士兵射击的整个过程,理解它是怎么样根据武器来创建弹盒,然后加载子弹。现在来分析子弹是怎么伤害到对方的过程。 继续前面的分析,它创建了子弹类Bullet,在这个类里实现爆炸效果和伤害转化。类Bullet也是由它的信息类Bulle…...
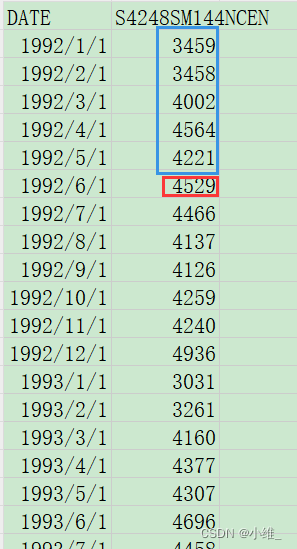
基于Pytorch框架的LSTM算法(一)——单维度单步滚动预测(2)
#项目说明: 说明:1time_steps滚动预测代码 y_norm scaler.fit_transform(y.reshape(-1, 1)) y_norm torch.FloatTensor(y_norm).view(-1)# 重新预测 window_size 12 future 12 L len(y)首先对模型进行训练; 然后选择所有数据的后wind…...
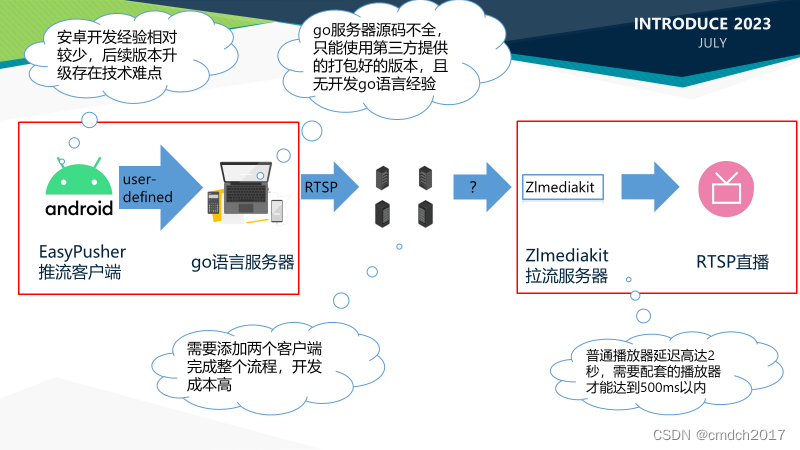
安全操作(安卓推流)程序
★ 安全操作项目 项目描述:安全操作项目旨在提高医疗设备的安全性,特别是在医生离开操作屏幕时,以减少非授权人员的误操作风险。为实现这一目标,我们采用多层次的保护措施,包括人脸识别、姿势检测以及二维码识别等技术…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...
