noip模拟赛多校第八场 T3 遥控机器人 (最短路 + 技巧拆点)
题面
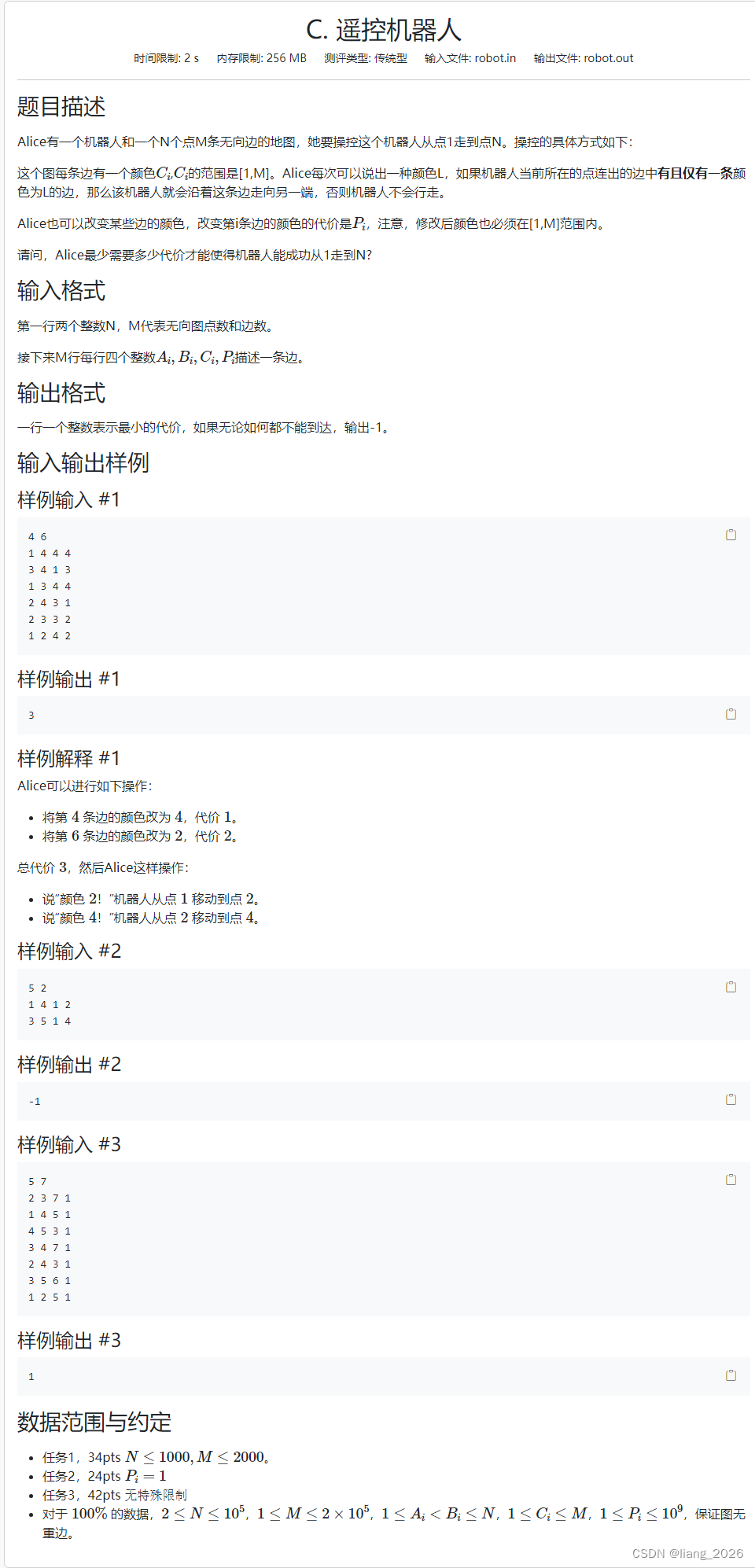
简要题意:
给你一个 n n n 个点 m m m 条边的图。边 i i i 有颜色 c i c_i ci。你可以选择一些边改变它们的颜色成为区间 [ 1 , m ] [1, m] [1,m] 中的任意颜色,改变一条边 i i i 一次的代价是 w i w_i wi。询问你能否在一些改变操作后使得可以从 1 1 1 号点,每次只经过当前点的 特殊边 到达 n n n。特殊边的定义是 对于当前点而言,特殊边的颜色在该点所有出边中有且仅出现一条。 如果可以,输出最小代价。否则输出 − 1 -1 −1。
分析:
凭感觉是一道最短路的题。
首先有一个性质:因为颜色的区间与边数相同,所以如果要改变一条边,那么可以把它变成一个任何别的边都不会再变成的颜色。换言之, 如果要花费代价改变某一条边的颜色,那么可以把它变成无色,并且这样是最优的。
接下来我们考虑如果一条边 ( u , v ) (u, v) (u,v) 的颜色是 c c c,花费是 w w w。我们从 u u u 到 v v v 经过它花费代价有几种情况:
1. u u u 的出边中是 c c c 颜色的只有一条,那么代价是 0 0 0。
2. u u u 的出边中 c c c 颜色的边有多条,改变这条边的颜色至无色,花费是 w w w。
3. u u u 的出边中 c c c 颜色的边有多条,改变不改变它的颜色,改变其它边的颜色至无色。
花费是 v a l u , c − w val_{u, c} - w valu,c−w。 v a l u , c val_{u, c} valu,c 代表所有 u u u 的出边中颜色是 c c c 的边的代价之和。
不难发现,情况 1 1 1 可以归到情况 3 3 3 中。
我们考虑把这两种代价看做两种边权跑最短路会有什么问题:
如果按照情况 3 3 3 从 u u u 到 v v v,我们考虑会不会存在一个问题:按照情况 3 3 3 我们需要把其它颜色也为 c c c 的边都改成无色,那么把它变成无色但是却不记录会不会影响后面答案的计算呢?
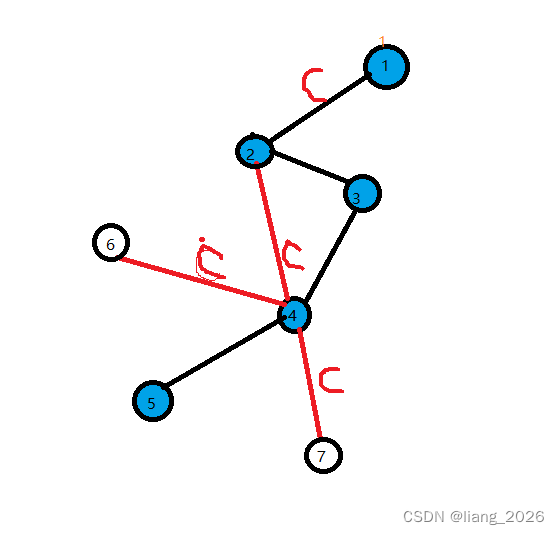
蓝色点表示最优路径的点,红色的边表示情况 3 3 3 中染成无色的边,它们的颜色是 c c c。黑色的边表示最优路径的边。那么如果出现上图的情况(从 5 5 5 号点走到 1 1 1 号点),那么 2 2 2 号点到 1 1 1 号点似乎是不需要花费的,因为在从 4 4 4 号点到 3 3 3 号点的时候就把那条颜色为 c c c 的边染成了无色。但是我们按照上面的规则进行的话,如果从 2 2 2 到 3 3 3 还使用情况 3 3 3,显然会多算一个代价。
但是深入思考一下,这种情况不会发生。因为这样的路径一定不是最优路径。如果按照上图的走法,那么 ( 2 , 4 ) (2,4) (2,4) , ( 6 , 4 ) (6, 4) (6,4), ( 4 , 7 ) (4, 7) (4,7) 的代价都会被算。实际上如果我们直接选择路径 5 → 4 → 2 → 1 5 \to 4 \to 2 \to 1 5→4→2→1,并且 ( 4 , 2 ) (4, 2) (4,2) 使用情况 2 2 2, ( 2 , 1 ) (2, 1) (2,1) 使用情况 3 3 3 肯定更加优秀。
这也就意味着: 如果我们能够通过某种方式处理好情况 2 2 2 带来的影响(即把边染成无色的影响),那么按照上面的规则跑最短路就是对的。
如果按照情况 2 2 2 经过一条颜色为 c c c 的边 从 u u u 到 v v v,那么 ( u , v ) (u, v) (u,v) 这条边颜色的改变可能会影响从 v v v 到 k k k 经过一条颜色为 c c c 按照情况 3 3 3 所花费的代价。根据这个问题,我们考虑 拆点。
有一个很暴力的想法是我们把每一个点拆成 m + 1 m + 1 m+1 个点:若有三个点 a a a, b b b , c c c。 a a a 到 b b b 经过一条颜色为 x x x 的边,当使用情况 2 2 2 的时候,可以从 a a a 走向 b x b_x bx,代价为 0 0 0, b x b_x bx必须继续沿着颜色x使用情况 3 3 3 走向其他点。每一个点的 0 0 0 状态表示 没有限制。这样我们就解决了维护信息的问题。但是复杂度好像有点问题。
我们考虑实际上一个点没有必要开 m m m 个点,只需要对每个点开其存在的颜色数个点就行了。一条边能够提供给两个点分别提供 1 1 1 个点,所以总点数是 2 m + n 2m + n 2m+n。然后建图跑最短路即可。时间复杂度 O ( ( n + m ) l o g 2 ( n + m ) ) O((n + m)log_2(n + m)) O((n+m)log2(n+m))。常数有亿点大。
CODE:
#include<bits/stdc++.h>//拆点 把点的状态拆一下
using namespace std;
const int N = 1e5 + 10;
const int M = 2e5 + 10;
const int T = 2 * N + M * 2;
typedef pair< int, int > PII;
typedef long long LL;
inline int read(){int x = 0, f = 1; char c = getchar();while(!isdigit(c)){if(c == '-') f = -1; c = getchar();}while(isdigit(c)){x = (x << 1) + (x << 3) + (c ^ 48); c = getchar();}return x * f;
}
int u, v, c;
int n, m, head[T], ut[M], vt[M], ct[M], tot, len;//最多T个点
bool vis[T];
LL wt[M], dis[T], res, w;
map< PII, int > rk;
map< PII, LL > val;
struct edge{int v, last;LL w;
}E[M * 8 + 10000];
void add(int u, int v, LL w){E[++len].v = v;E[len].last = head[u];E[len].w = w;head[u] = len;
}
struct state{int x; LL w;friend bool operator < (state a, state b){return a.w > b.w;}
};
void dijkstra(int s){priority_queue< state > q;q.push((state){s, 0});while(!q.empty()){state u = q.top(); q.pop();int x = u.x;if(vis[x]) continue;vis[x] = 1;for(int i = head[x]; i; i = E[i].last){int v = E[i].v; LL w = E[i].w;if(dis[v] > dis[x] + w){dis[v] = dis[x] + w;q.push((state){v, dis[v]});}}}
}
int main(){n = read(), m = read();for(int i = 1; i <= n; i++){rk[make_pair(i, 0)] = ++tot;}for(int i = 1; i <= m; i++){u = read(), v = read(); c = read(), w = 1LL * read();if(!rk[make_pair(u, c)]) rk[make_pair(u, c)] = ++tot;if(!rk[make_pair(v, c)]) rk[make_pair(v, c)] = ++tot;val[make_pair(u, c)] += w;val[make_pair(v, c)] += w;ut[i] = u, vt[i] = v, wt[i] = w, ct[i] = c;}for(int i = 1; i <= m; i++){int u = ut[i], v = vt[i], c = ct[i], w = wt[i];add(rk[make_pair(u, 0)], rk[make_pair(v, 0)], w);//改变颜色,不做限制 add(rk[make_pair(u, 0)], rk[make_pair(v, c)], 0);//改变颜色,必须限制 add(rk[make_pair(u, c)], rk[make_pair(v, 0)], val[make_pair(u, c)] - w);add(rk[make_pair(u, 0)], rk[make_pair(v, 0)], val[make_pair(u, c)] - w);add(rk[make_pair(v, 0)], rk[make_pair(u, 0)], w);//改变颜色,不做限制 add(rk[make_pair(v, 0)], rk[make_pair(u, c)], 0);//改变颜色,必须限制 add(rk[make_pair(v, c)], rk[make_pair(u, 0)], val[make_pair(v, c)] - w);add(rk[make_pair(v, 0)], rk[make_pair(u, 0)], val[make_pair(v, c)] - w);}memset(dis, 0x3f, sizeof dis);dis[rk[make_pair(1, 0)]] = 0;dijkstra(rk[make_pair(1, 0)]);res = dis[rk[make_pair(n, 0)]];if(res == 0x3f3f3f3f3f3f3f3f) res = -1;printf("%lld\n", res);return 0;
}相关文章:

noip模拟赛多校第八场 T3 遥控机器人 (最短路 + 技巧拆点)
题面 简要题意: 给你一个 n n n 个点 m m m 条边的图。边 i i i 有颜色 c i c_i ci。你可以选择一些边改变它们的颜色成为区间 [ 1 , m ] [1, m] [1,m] 中的任意颜色,改变一条边 i i i 一次的代价是 w i w_i wi。询问你能否在一些改变…...

高防IP的原理
高防IP,把域名解析到高防IP上(web事务只要把域名指向高防IP 即可。非web事务,把事务IP换成高防IP即可)一起在高防IP上设置转发规矩;所有公网流量都会走高防IP,通过端口协议转发的方法将用户的拜访通过高防IP转发到源站IP,一起将歹…...

Apache Doris (五十一): Doris数据缓存
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录 1....

一、配置环境
一、配置Java环境 确保安装了Java开发工具包(JDK),并且设置了JAVA_HOME环境变量。 二、配置FFmpeg环境 如果使用了FFmpeg相关的功能,需要确保系统中已经安装了FFmpeg,并且设置了FFMPEG_HOME环境变量。 ffmpeg安装教…...

各种 sql 语句
sql 语句: SELECT max(val) as level_max_val from (select greatest(level1,level2,level3,level4,level5,level6,level7,level8,level9,level10) as val from kbt_2020cv52_data) k;...
CentOS/RHEL7环境下更改网卡名称为CentOS6的传统命名规则
图片 CentOS/RHEL7网卡命名规则介绍 图片 传统的Linux服务器网卡的名称命名方式是从eth0,eth1,eth2....这种方式命名的,但是这个编号往往不一定准确对应网卡接口的物理顺序,常规模式下我们使用的服务器设备可能只有一张网卡,若网卡较多的情…...
飞书开发学习笔记(三)-利用python开发调试云文档和电子表格
飞书开发学习笔记(三)-利用python开发调试云文档和电子表格 一.建立Python飞书开发环境 首先还是进入开放平台下的API调试台 飞书开放平台:https://open.feishu.cn/app?langzh-CN 以获取"我的空间"下的文件清单为例,通过获取飞书API调试台提…...
爆火的正规号卡推广分销 流量卡分销代理平台
正规号卡推广和流量卡分销代理可以通过“聚量推客”申请 聚量推客上的号卡单价高 数据及时 结算快,你还可以搭配平台上的拉新产品各种推广场景,更值得拥有哦...

Gin框架入门实战系列教程之Gin环境搭建 Gin程序的热加载 Gin路由 GET POST PUT DELETE
Gin框架入门实战系列教程之Gin环境搭建 Gin程序的热加载 Gin路由 GET POST PUT DELETE 主讲教师:(大地) 在线文档见网盘下载: 百度网盘 请输入提取码 提取码:abcd 一、Gin介绍 Gin 是一个 Go (Golang) 编写的轻量级…...

浏览器自动播放音视频-前端实现方案
目录 前言 浏览器自动播放策略 策略详情: 实现方案 方案1: 互动后播放 方案2: 互动后出声 总结 前言 在开发中可能有遇到这样的需求,当用户打开页面后,需要自动播放视频或音频,按理说那就打开页面…...

HttpUtils工具类
作为Java开发程序员,需要我们经常写一些工具类来简化开发过程,我们自己肯定写过或者用过HttpUtils用来发送http请求,但是每次手写太繁琐了,于是就按照标准写了一个Http工具类,现在分享出来。 1.HTTP请求简介 HTTP(Hy…...

AI:59-基于深度学习的行人重识别
🚀 本文选自专栏:AI领域专栏 从基础到实践,深入了解算法、案例和最新趋势。无论你是初学者还是经验丰富的数据科学家,通过案例和项目实践,掌握核心概念和实用技能。每篇案例都包含代码实例,详细讲解供大家学习。 📌📌📌在这个漫长的过程,中途遇到了不少问题,但是…...
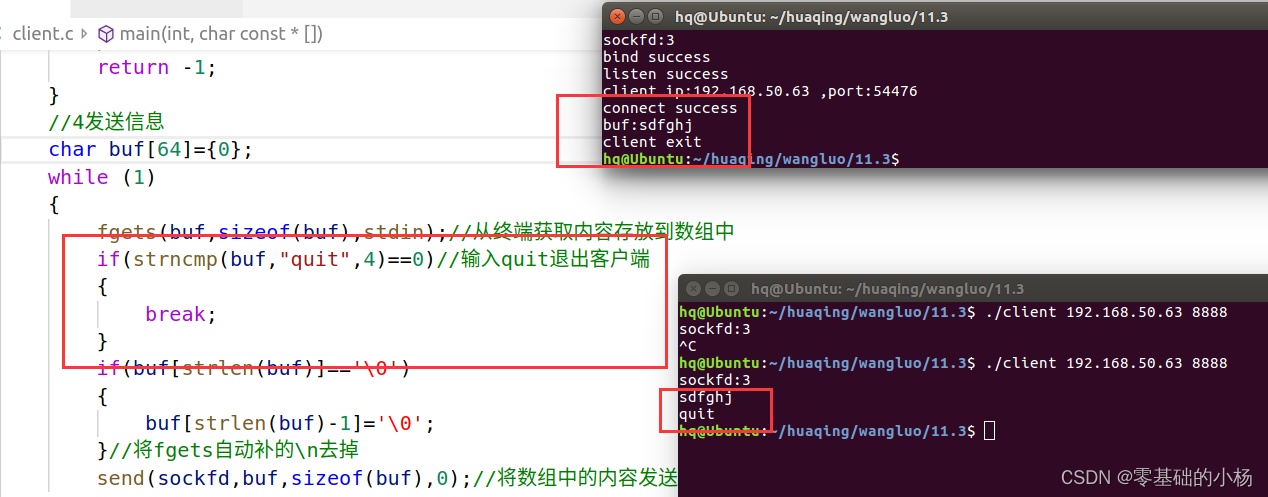
TCP编程及基础知识
一、端口号 为了区分一台主机接收到的数据包应该转交给哪个进程来进行处理,使用端口号来区分TCP端口号与UDP端口号独立端口用两个字节来表示 2byte(65535个) 众所周知端口:1~1023(1~255之间为众所周知端口ÿ…...
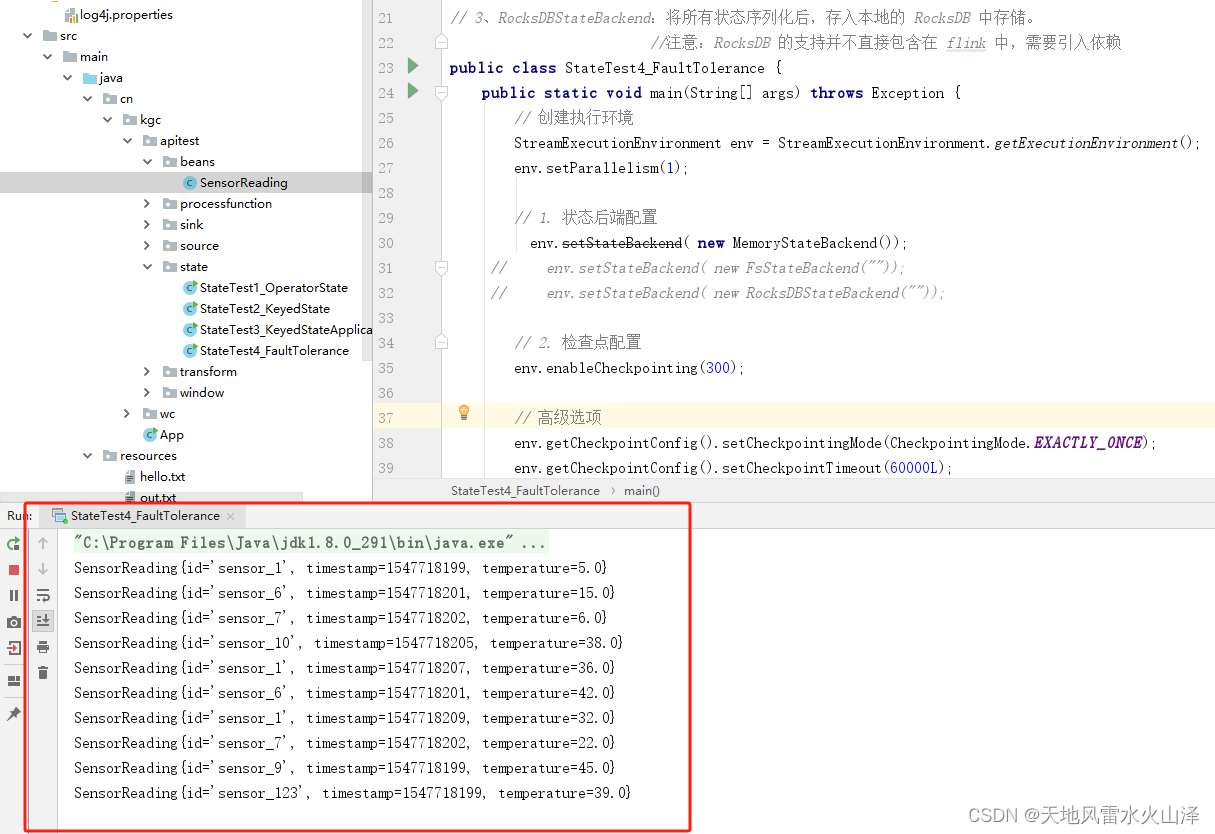
二百零一、Flink——Flink配置状态后端运行后报错:Can not create a Path from an empty string
一、目的 在尚硅谷学习用Flink配置状态后端的项目中,运行报错Exception in thread "main" java.lang.IllegalArgumentException: Can not create a Path from an empty string 二、Flink的状态后端(state backend)类型 (一)Memo…...

Python 爬虫基础
Python 爬虫基础 1.1 理论 在浏览器通过网页拼接【/robots.txt】来了解可爬取的网页路径范围 例如访问: https://www.csdn.net/robots.txt User-agent: * Disallow: /scripts Disallow: /public Disallow: /css/ Disallow: /images/ Disallow: /content/ Disallo…...

亚马逊云科技大语言模型的创新科技
陈老老老板🤴 🧙♂️本文专栏:生活(主要讲一下自己生活相关的内容)生活就像海洋,只有意志坚强的人,才能到达彼岸。 🧙♂️本文简述:亚马逊云科技大语言模型的创新科技 🧙♂️上…...

Qt 各种数据类型
目录 1. 基础类型 2. log 输出 3. 字符串类型 3.2 QByteArray 构造函数 数据操作 子字符串查找和判断 遍历 查看字节数 类型转换 3.3 QString 4. QVariant 4.1 标准类型 4.2 自定义类型 5. 位置和尺寸 5.1 QPoint 5.2 QLine 5.3 QSize 5.4 QRect 6. 日期和…...
电动车展示预约小程序的作用如何
电动车可以说是现在出行常见的方法,覆盖年龄广几乎是每家必备,也有不小大小品牌和经销商,市场需求较高,但在实际经营中,对经销商来时也面临着一些痛点: 1、品牌传播产品展示难 不同品牌竞争很大ÿ…...

「随笔」浅谈2023年云计算的发展趋势
在2023年,云计算的发展趋势将受到政治、经济、社会和科技四个维度的影响。以下是对这些维度的具体分析: 1.1 政治维度: 全球政策推动: 随着全球各国政策对云计算的重视程度不断提高,云计算服务将获得更广泛的市场准入…...

高性能三防工业平板电脑 防摔防爆电容屏工控平板
HT1000是一款高性能工业三防平板,10.1英寸超清大屏,厚度仅14.9mm,超薄机身,可轻松插入袋中,方便携带,搭载8核2.0GHz高性能CPU,行业领先的Android 11.0,设备性能大幅提升,…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
