「掌握创意，释放想象」——Photoshop 2023，你的无限可能！
Adobe Photoshop 2023(PS2023) 来了,全世界数以百万计的设计师、摄影师和艺术家使用 Photoshop 将不可能变为可能。从海报到包装，从基本的横幅到漂亮的网站，从令人难忘的徽标到引人注目的图标，Photoshop 2023让创意世界不断前进。借助直观的工具和易于使用的模板，即使是初学者也可以做出惊人的事情。
在数字创意领域，Photoshop一直是业内最受欢迎和广泛应用的设计工具之一。而随着全新推出的Photoshop 2023，这款经典软件迈向了一个全新的里程碑。作为Adobe Creative Suite的核心产品，Photoshop 2023注重提升用户的创作体验、增强工作效率，并引入了一系列令人激动的功能和改进。
首先，Photoshop 2023带来了更加智能化的编辑工具。通过AI技术的加持，新版Photoshop能够更准确地识别和提取图像中的元素，使用户在编辑、合成和修饰图像时更加高效。智能修复工具和内容感知填充功能的升级，进一步简化了瑕疵修复和背景填充的过程，让你能够将更多时间投入到创造性的设计中。
其次，Photoshop 2023还引入了全新的3D设计和渲染功能。借助内置的3D工具和材质库，你可以轻松地创建逼真的三维场景和物体，并进行灯光、纹理和渲染的调整。无论是为产品设计制作宣传图，还是为游戏开发制作精美的角色模型，Photoshop 2023都能满足你的需求，并带来惊人的效果。
此外，Photoshop 2023在工作流程和协作方面也有所改进。全新的云同步功能使团队成员能够方便地共享和协作编辑项目文件，实现更高效的工作流程。无论你是与团队合作还是个人创作，Photoshop 2023都能提供顺畅的协作体验，让你更好地与他人分享创意并获得反馈。
最后，Photoshop 2023注重用户个性化的定制化。你可以根据自己的喜好和工作习惯，自定义工作区、快捷键和面板布局，使软件界面符合你的需求，提高工作效率。无论你是一名摄影师、插画师还是平面设计师，Photoshop 2023都将成为你创造力的最佳伙伴。
总之，Photoshop 2023以其强大的功能和卓越的性能，为数字艺术家、设计师和创作者带来了更多可能性。无论你是初学者还是专业人士，Photoshop 2023都能满足你对图像处理和创作的需求。让我们一起掌握创意，释放想象，开启属于你的创作之旅吧！
Mac安装：Photoshop 2023 for mac(PS 2023)v24.7中/英文激活版
Win安装：Adobe Photoshop 2023(PS2023)v24.7.1.741 (x64)直装版
相关文章：
「掌握创意，释放想象」——Photoshop 2023，你的无限可能！
Adobe Photoshop 2023(PS2023) 来了,全世界数以百万计的设计师、摄影师和艺术家使用 Photoshop 将不可能变为可能。从海报到包装，从基本的横幅到漂亮的网站，从令人难忘的徽标到引人注目的图标，Photoshop 2023让创意世界不断前进。借助直观的工…...
SQLSugar查询返回DataTable
SQLSugar是一个用于执行SQL查询的C#库，它提供了简单易用的API接口来执行SQL查询。要查询返回DataTable，可以使用SQLSugar的QueryHelper类。 以下是一个示例代码，展示了如何使用SQLSugar的QueryHelper类查询返回DataTable： 首先&…...
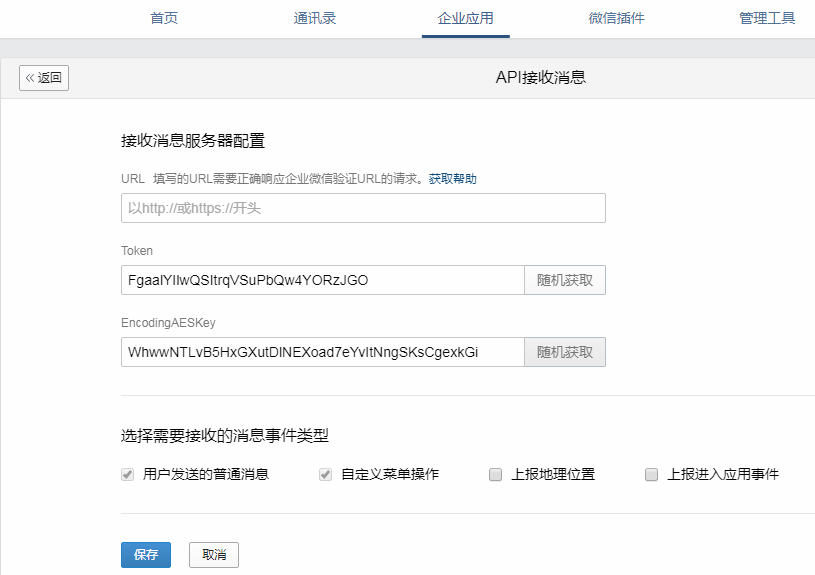
企业微信开启接收消息+验证URL有效性
企业微信开启接收消息验证URL有效性 📔 千寻简笔记介绍 千寻简笔记已开源，Gitee与GitHub搜索chihiro-notes，包含笔记源文件.md，以及PDF版本方便阅读，且是用了精美主题，阅读体验更佳，如果文章对…...
电脑访问不到在同网络的手机设备
手机连接了同网络的wifi，但是电脑ping不通手机的ip，这可能是路由出了问题，因为最终是走的mac地址，访问不了是因为电脑不知道手机的mac地址，则可以这样设置绑定mac地址，管理员权限启动cmd，然后执…...
国内MES系统应用研究报告：“企业MES应用现状”| 百世慧®
随着制造企业数字化转型需求的增强，工业软件的需求也不断被激发。 2022年，中国MES软件及服务市场规模实现23.8%的较高速增长。同时，随着工业互联网、MOM的兴起和不断发展，也推动着MES持续发展和不断迭代，如今MES向着更…...
C++模板元模板实战书籍讲解第一章题目讲解
目录 第一题 C代码示例 第二题 C代码示例 第三题 3.1 使用std::integral_constant模板类 3.2 使用std::conditional结合std::is_same判断 总结 第四题 C代码示例 第五题 C代码示例 第六题 C代码示例 第七题 C代码示例 总结 第一题 对于元函数来说，…...
Java在互联网网络安全中的应用（三）
目录 1. 互联网网络安全概述 2. Java的网络安全特性 3. 用Java加固网络应用 4. 安全传输 5. 安全框架和工具 6. 实际应用案例 7. 最佳实践和资源 目标 本次技术分享的目标是介绍Java技术在互联网网络安全中的应用，包括关键概念、最佳实践和实际案例。 1. 互…...
VMLogin如何解决跨境电商多账号管理难题？
做跨境电商的，比如亚马逊、eBay这些卖家。随着团队规模的扩大，或者多店铺运营，那么多个店铺多个账号管理就成为了一个困难。如何解决这个问题呢？ 首先来看看很多电商卖家多账号管理会面临的问题 经营者通常需要同时管理多个市场…...
STM32创建工程步骤
以创建led工程为例： 新建一个led文件夹 新建一个以led命名的工程（用keil_uVision5）并添加三个组。 Library文件夹里放置库函数文件。 User： 点亮led灯的程序； 直接给寄存器赋值 调用库函数。 #include "stm…...
软考 系统架构设计师系列知识点之边缘计算（1）
所属章节： 第11章. 未来信息综合技术 第4节. 边缘计算概述 1. 边缘计算概念 在介绍边缘计算之前，有必要先介绍一下章鱼。章鱼就是用“边缘计算”来解决实际问题的。作为无脊椎动物中智商最高的一种动物，章鱼拥有巨量的神经元，但…...
vue:写一个数组box和list数组，在保留box数组中原有对象的同时，将list数组中每一个对象插入到box数组后面
前言：由于源码涉及到后端调用数据和一些无关的功能所以我就专门针对这个功能的代码，这样好方便理解。 1、在data中定义两个数组：box和list，并给它们初始化值 data() {return {box: [/*初始的box数组对象*/],list: [/*初始的list…...
Python教程：随机函数，开始猜英文单词的游戏
开始猜英文单词的游戏… 总计生命次数：3次 -----------游戏开始中…----------- ？？？？请猜一个，4位数的单词:mafr 猜错了，再努力一下 -----------你还有2次生命------------ ma？&…...
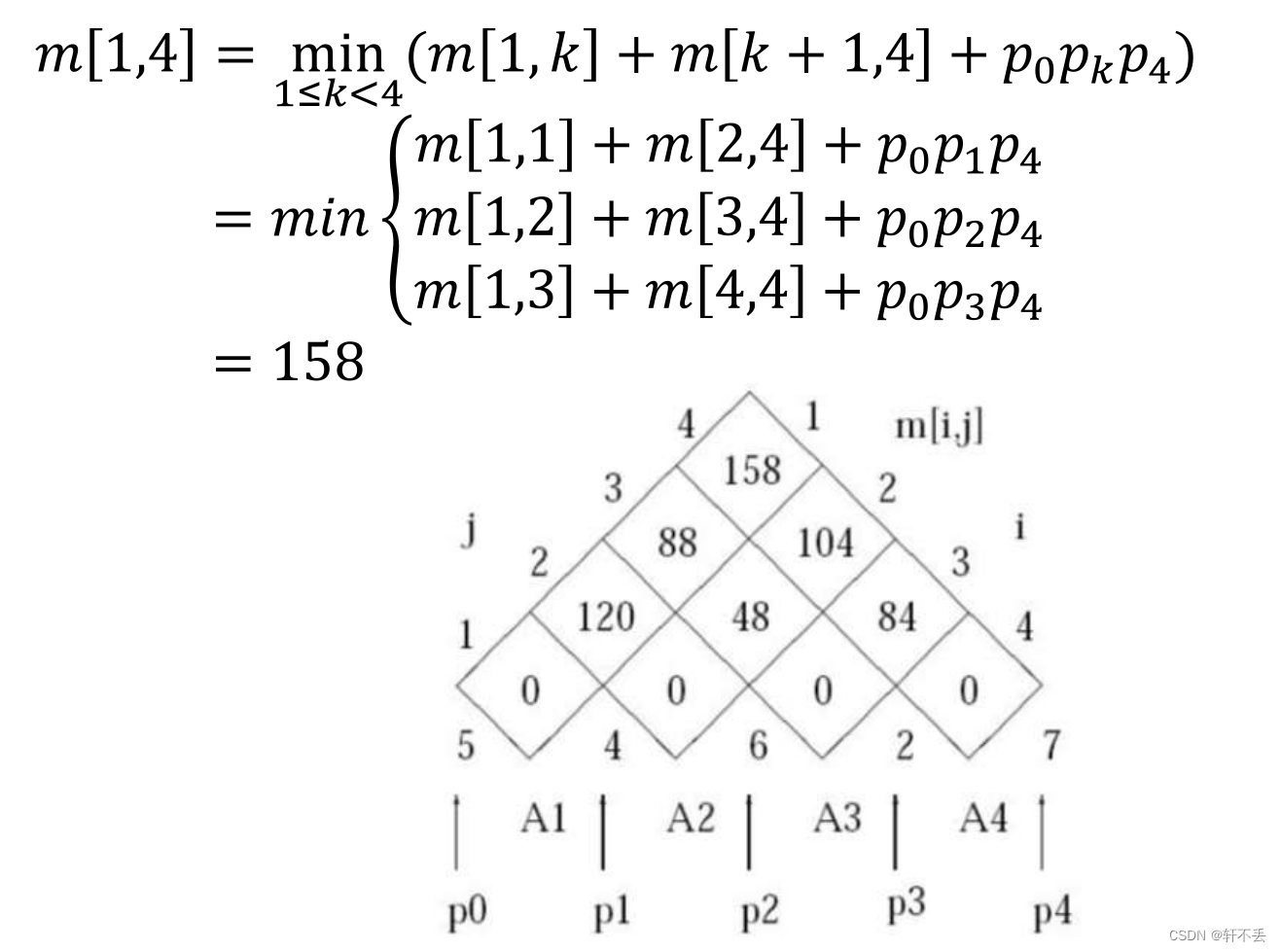
Unit2_1：动态规划DP
文章目录 一、介绍二、0-1背包问题问题描述分析伪代码时间复杂度 三、钢条切割问题问题描述分析伪代码过程 四、矩阵链乘法背景性质分析案例伪代码 一、介绍 动态规划类似于分治法,它们都将一个问题划分为更小的子问题 最优子结构:问题的最优解包含子问题的最优解。DP适用的原…...
k8s提交spark应用消费kafka数据写入elasticsearch7
一、k8s集群环境 k8s 1.23版本，三个节点，容器运行时使用docker。 spark版本时3.3.3 k8s部署单节点的zookeeper、kafka、elasticsearch7 二、spark源码 https://download.csdn.net/download/TT1024167802/88509398 命令行提交方式 /opt/module/spark…...
linux傻瓜式安装Java环境及中间件
linux配置Java环境及中间件 1.傻瓜式安装Java1.下载2.追加3.刷新测试 2.傻瓜式安装docker1.docker卸载2.docker安装 3.Docker傻瓜式安装Redis1.傻瓜式安装安装并配置 4.Docker傻瓜式安装RabbitMQ5.Docker傻瓜式安装MySql1.拉取2.配置 6.傻瓜式安装Nacos1.官网下载nacos2.SQL文件…...
javascript中的new原理及实现
在js中，我们通过new运算符来创建一个对象，它是一个高频的操作。我们一般只是去用它，而很少关注它是如何实现的，它的工作机制是什么。 1 简介 本文介绍new的功能，用法，补充介绍了不加new也同样创建对象的方…...
R语言 PPT 预习+复习
什么狗吧发明的结业考，站出来和我对线 第一章 绪论 吊码没有，就算考R语言特点我也不背，问就是叫么这没用。 第二章 R语言入门 x<-1:20 赋值语句 x 1到20在x上添加均值为0、标准差为2的正态分布噪声 y <- x rnorm (20, 0, 2) 这…...
轻松实现固定资产智能管理的工具来了
易点易动资产管理系统是一款旨在轻松实现智能资产管理的工具。固定资产管理对于企业的日常经营和可持续发展至关重要。然而，固定资产具有设备价值高、使用周期长、使用地点分散、使用环境恶劣、流动性强、安全管理难度大等特点，传统的管理方式往往无法高…...
软考高级系统架构设计师系列之：微服务
软考高级系统架构设计师系列之：微服务 一、微服务二、微服务的优势三、微服务挑战四、微服务与SOA的对比一、微服务 微服务架构建议将大型复杂的单体架构应用划分为一组微小的服务，每个微服务根据其负责的具体业务职责提炼为单一的业务能力。每个服务可以很容易地部署并发布…...
vue + axios + mock
参考来源：Vue mock.js模拟数据实现首页导航与左侧菜单功能_vue.js_AB教程网 记录步骤：在参考资料来源添加axios步骤 1、安装mock依赖 npm install mock -D //只在开发环境使用 下载完成后，项目文件package.json中的devDependencies就会加…...
SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）
HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...
rknn优化教程（二）
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK，开始写第二篇的内容了。这篇博客主要能写一下： 如何给一些三方库按照xmake方式进行封装，供调用如何按…...
盘古信息PCB行业解决方案：以全域场景重构，激活智造新未来
一、破局：PCB行业的时代之问 在数字经济蓬勃发展的浪潮中，PCB（印制电路板）作为 “电子产品之母”，其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透，PCB行业面临着前所未有的挑战与机遇。产品迭代…...
连锁超市冷库节能解决方案：如何实现超市降本增效
在连锁超市冷库运营中，高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术，实现年省电费15%-60%，且不改动原有装备、安装快捷、…...
Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候，写过一篇简单实现，后期随着对该模型的深入研究，本次记录涉及到prophet 的公式以及参数调优，从公式可以更直观…...
Frozen-Flask ：将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是：将一个 Flask Web 应用生成成纯静态 HTML 文件，从而可以部署到静态网站托管服务上，如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
反射获取方法和属性
Java反射获取方法 在Java中，反射（Reflection）是一种强大的机制，允许程序在运行时访问和操作类的内部属性和方法。通过反射，可以动态地创建对象、调用方法、改变属性值，这在很多Java框架中如Spring和Hiberna…...
laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
return this；返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请，不同级别的经理有不同的审批权限： // 抽象处理者：审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...