CF1866M Mighty Rock Tower
CF题面 luogu题面
期望题。
题目大意:一个人在搭积木,每次堆叠可能成功或失败,失败可能导致其下面连续的若干块掉落。给定搭每一块时失败的概率,求堆叠完成的期望次数。
具体的,假设当前正在堆叠第 i 块,设掉落概率为 p,则有 p 概率第 i 块失败,有 p 2 p^2 p2 概率第 i 块和第 i-1 块均掉落,有 p 3 p^3 p3 概率第 i, i-1, i-2 块均掉落,以此类推。
设 f i f_i fi 表示堆叠 i i i 块的期望次数不好转移,注意到堆叠连续性,考虑设 f i f_i fi 表示由第 i − 1 i-1 i−1 块到堆好第 i i i 块的期望次数。
列出状态转移方程:
f i = ( 1 − p i ) × 1 + p i ( ( 1 − p i ) ( f i + 1 ) + p i ( ( 1 − p i ) ( f i + f i − 1 + 1 ) + ⋯ + p i ( f i + f i − 1 + ⋯ + f 1 + 1 ) … ) ) f_i=(1-p_i)\times 1+p_i((1-p_i)(f_i+1)+p_i((1-p_i)(f_i+f_{i-1}+1)+\dots+p_i(f_i+f_{i-1}+\dots+f_1+1)\dots)) fi=(1−pi)×1+pi((1−pi)(fi+1)+pi((1−pi)(fi+fi−1+1)+⋯+pi(fi+fi−1+⋯+f1+1)…))
变形得 f i ( 1 − p i ) = 1 + p i 2 × f i − 1 − p i 3 × f i − 1 + p i 3 × ( f i − 1 + f i − 2 ) + ⋯ + p i i − 1 ( f i − 1 + f i − 2 + ⋯ + f 2 ) + p i i ( f i − 1 + f i − 2 + ⋯ + f 2 + f 1 ) f_i(1-p_i)=1+p_i^2\times f_{i-1}-p_i^3\times f_{i-1}+p_i^3\times (f_{i-1}+f_{i-2})+\dots+p_i^{i-1}(f_{i-1}+f_{i-2}+\dots+f_2)+p_i^i(f_{i-1}+f_{i-2}+\dots+f_2+f_1) fi(1−pi)=1+pi2×fi−1−pi3×fi−1+pi3×(fi−1+fi−2)+⋯+pii−1(fi−1+fi−2+⋯+f2)+pii(fi−1+fi−2+⋯+f2+f1)
化简 得 f i = 1 + ∑ j = 2 i p i j × f i − j + 1 1 − p i f_i=\large\frac{1+\sum^{i}_{j=2}p_i^j\times f_{i-j+1}}{1-p_i} fi=1−pi1+∑j=2ipij×fi−j+1
这时复杂度是 O ( N 2 ) O(N^2) O(N2),考虑如何优化。
我们当然想将 f i − j + 1 f_{i-j+1} fi−j+1 转成前缀和,麻烦在于 p i j p_i^j pij,这时我的思路卡死。
考虑如何处理 p p p,发现 p ∈ [ 0 , 100 ) p\in[0,100) p∈[0,100),于是可以考虑对于所有 p p p 都做前缀和维护。
这里再细讲下如何前缀和维护。对于 ∑ j = 2 i P j × f i − j + 1 \sum^{i}_{j=2}P^j\times f_{i-j+1} ∑j=2iPj×fi−j+1,观察 i + 1 i+1 i+1 的和,即 ∑ j = 2 i + 1 P j × f i − j + 2 \sum^{i+1}_{j=2}P^j\times f_{i-j+2} ∑j=2i+1Pj×fi−j+2,发现就是 前者 × P + P 2 × f i \times P+P^2\times f_i ×P+P2×fi。如果把求和的式子改写成 ∑ j = 1 i − 1 P i i − j + 1 × f j \sum^{i-1}_{j=1}P_i^{i-j+1}\times f_j ∑j=1i−1Pii−j+1×fj 会好看些,这里不写了。当然,学会观察式子并将之改得更加容易理解也是一种技能。
然后这题就做完了,时间复杂度 O ( 100 N log M ) O(100N\log M) O(100NlogM)。
这题时限 2s,注意优化常数。
优化后的复杂度是 O ( 100 N ) O(100N) O(100N),可以通过此题。
这题的关键点在于发现 p ∈ [ 0 , 100 ) p\in[0,100) p∈[0,100) ,可以将前缀和关于 p p p 全部维护出来。
相关文章:

CF1866M Mighty Rock Tower
CF题面 luogu题面 期望题。 题目大意:一个人在搭积木,每次堆叠可能成功或失败,失败可能导致其下面连续的若干块掉落。给定搭每一块时失败的概率,求堆叠完成的期望次数。 具体的,假设当前正在堆叠第 i 块,…...
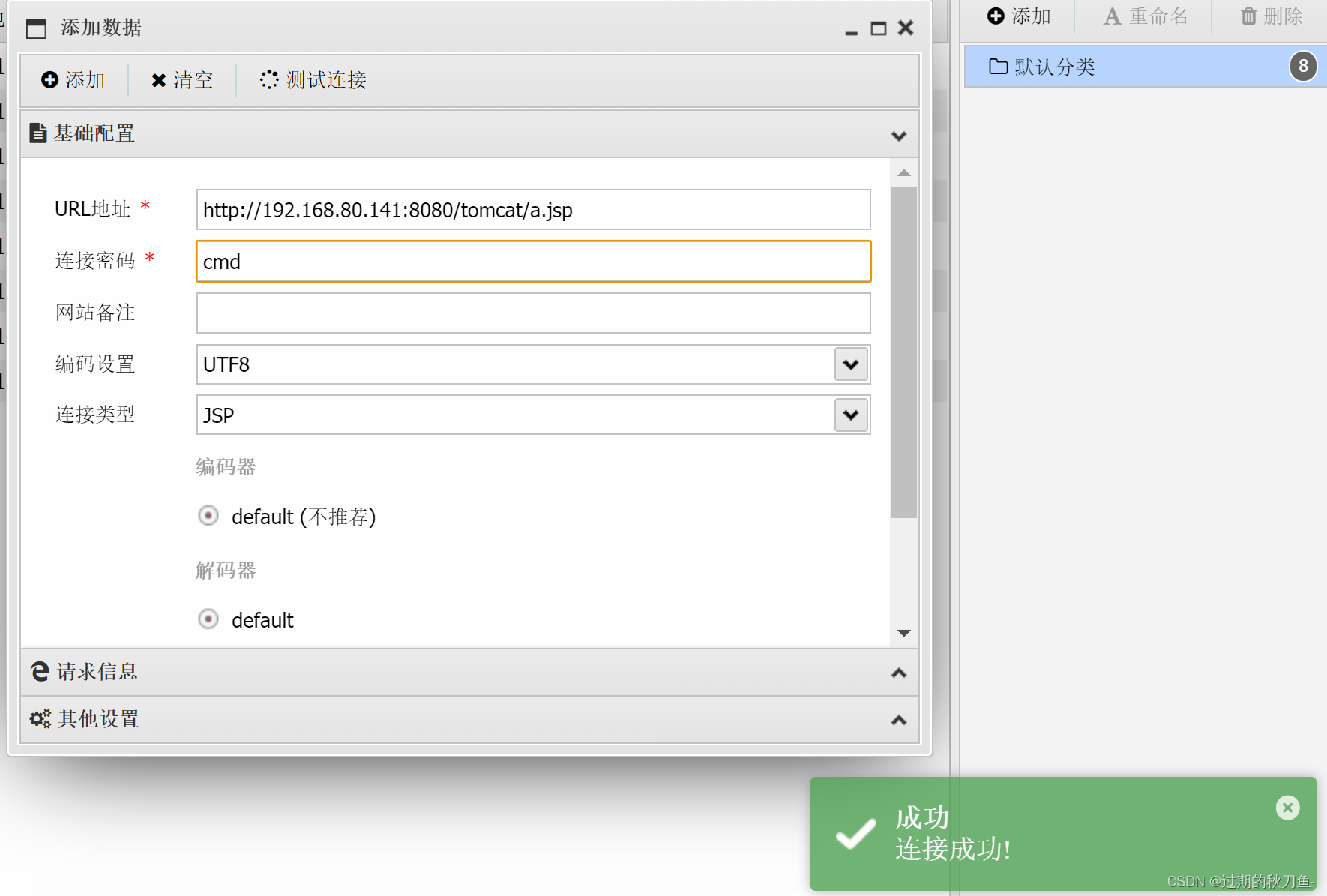
【漏洞复现】Apache_Tomcat7+ 弱口令 后台getshell漏洞
感谢互联网提供分享知识与智慧,在法治的社会里,请遵守有关法律法规 文章目录 1.1、漏洞描述1.2、漏洞等级1.3、影响版本1.4、漏洞复现1、基础环境2、漏洞扫描3、漏洞验证 说明内容漏洞编号漏洞名称Tomcat7 弱口令 && 后台getshell漏洞漏洞评级高…...

2023-11-7 OpenAI 45 分钟发布会:演示关于 GPT Store 构建 GPT、零代码创建 AI Agent
本心、输入输出、结果 文章目录 2023-11-7 OpenAI 45 分钟发布会:演示关于 GPT Store 构建 GPT、零代码创建 AI Agent前言Sam Altman 正在创建一个「创业导师 GPT」零代码创建 AI AgentAssistants API 封装的能力包括 Sam Altman 对发布会总结相关链接弘扬爱国精神 …...

嵌入式系统中的FPGA
举个栗子 假设你有一台智能家居系统,其中的FPGA可以被类比为智能家居中的中央控制器。 智能家居系统: 定制家居逻辑: 你希望智能家居系统能够根据你的生活习惯、时间表和喜好自动控制灯光、温度、窗帘等设备。就像FPGA中可以根据需求重新配置…...

String,StringBulider,StringBuffer的简单说明
目录 1.String 2.StringBuffer 3.StringBuilder 4.线程安全的验证 1.String String是声明在java.lang下的一个类。 String被定义为final,表示不能被继承。内部定义了final char value[]用于存储字符串数据,所以String对象的值是不可改变的。每次对S…...
)
Python编程题集(第一部分基本语法基础)
Demo01 摄氏温度转化为华氏温度 题目描述: 输入一个摄氏温度的值,将它转变为华氏温度,并将结果输出 转换的公式为如下:fahrenheit (9 / 5 ) * celsius 32 输入输出描述 输入一个值表示摄氏温度celsius 输出华氏温度fahren…...
手动关闭PS中的TopazStudio2的登录窗口
2021 adobe photoshop Topaz Studio 2 不是使用防火墙出站规则,是手动关闭的解决方案 点击社区-切换用户,登录窗口会出现X,可以手动关闭...

[elastic 8.x]java客户端连接elasticsearch与操作索引与文档
初始化客户端 引入相关依赖 <dependency><groupId>co.elastic.clients</groupId><artifactId>elasticsearch-java</artifactId><version>8.10.2</version> </dependency>初始化客户端 为了方便演示,我关闭了ela…...

接口测试总结
本文主要分为两个部分: 第一部分:主要从问题出发,引入接口测试的相关内容并与前端测试进行简单对比,总结两者之前的区别与联系。但该部分只交代了怎么做和如何做?并没有解释为什么要做? 第二部分࿱…...

计算机基础知识44
overflow溢出属性 visible:默认值,内容不会被修剪,会呈现在元素框之外。hidden:内容会被修剪,并且其余内容是不可见的。scroll:内容会被修剪,但是浏览器会显示滚动条以便查看其余的内容。auto: …...

【StringBuilder和StringBuffer】
文章目录 StringBuilder和StringBufferString类、StringBuilder和StringBuffer的区别 StringBuilder和StringBuffer的区别StringBuilder 字符串逆置 StringBuilder和StringBuffer String类、StringBuilder和StringBuffer的区别 String类的特点是不可变性,所以Stri…...

用java代码实现security
Java中security的实现主要涉及到以下几个方面: 认证(Authentication) 认证是确认用户身份的过程,Java中提供了不同的认证机制来保护应用程序不被未授权的用户访问。常用的认证机制有以下几种: 基于口令的认证:要求用户输入用户名…...

【Java 进阶篇】Java Session 原理及快速入门
大家好,欢迎来到本篇博客。今天,我们将探讨Java Web开发中一个重要而令人兴奋的概念,即Session(会话)。Session是一种在Web应用程序中跟踪用户状态和数据的机制。我们将深入了解Session的原理,并通过示例来…...

MoveFunsDAO 星航计划|从Move入门Web3与深入实践「公益课堂」
Move 语言作为最安全的编程语言之一,在资产的安全性和保护方面有着显著优势,被寄予引领 Web3 世界的全新叙事的厚望。 随着 Sui 在今年五月主网上线,它为 Move 生态带来一股新的浪潮。上线以来,Sui 公链的开发活跃度持续数月位居…...
)
RabbitMQ常用命令(一)
启动和关闭 1、启动RabbitMQ rabbitmq-server start & 注意:这里可能会出现错误,错误原因是/var/lib/rabbitmq/.erlang.cookie文件权限不够。 解决方案对这个文件授权 chown rabbitmq:rabbitmq /var/lib/rabbitmq/.erlang.cookie chmod 400 /va…...

在教育领域,AI垂直大模型应用场景总结!
1. 智能教育助手: 这种模型可以通过语音或文本与学生进行交互,提供个性化的学习建议和答疑解惑。根据学生的学习习惯和知识水平,推荐适合的学习资源,并提供实时的辅导和反馈。 2. 智能作文批改助手: 这种模型可以对…...
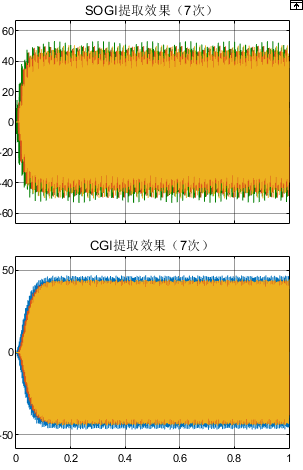
基于级联广义积分器(CGI)的谐波信号提取MATLAB仿真
微❤关注“电气仔推送”获得资料(专享优惠) 此方法可用于信号检测、虚拟阻抗合成、锁相环等方面。 在现有的信号提取方法中,众多学者采用了SOGI法、LPF法以及正交信号发生器等方法。当输入信号中不存在直流分量,只有谐波分量时&…...
Linux--线程-条件控制实现线程的同步
1.条件变量 条件变量是线程另一可用的同步机制。条件变量给多个线程提供了一个会合的场所。条件变量与互斥量一起使用时,允许线程以无竞争的方式等待特定的条件发生。 条件本身是由互斥量保护的。线程在改变条件状态前必须首先锁住互斥量,其他线程在获…...

flutter开发报错The instance member ‘widget‘ can‘t be accessed in an initializer
文章目录 问题描述问题原因解决方法 问题描述 The instance member ‘widget’ can’t be accessed in an initializer. 问题原因 “The instance member ‘widget’ can’t be accessed in an initializer” 错误是因为在初始化器列表中(constructor initializer…...

spring项目详细结构目录
这里写目录标题 一、项目结构1、model模型类Student2、mapper 数据访问层接口和映射文件接口类StudentMapper接下来创建名为 StudentMapper.xml 的映射文件 3、service 服务层接口和实现类创建名为 StudentService 的 Java 接口创建名为 StudentServiceImpl 的实现类 4、contro…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
