多目标最优化的资产配置
摘要及声明
1:本文主要对基于均值方差最优化的资产配置方法进行拓展,从多目标最优化的角度看待资产配置并可视化展示;
2:本文主要为理念的讲解,模型也是笔者自建,文中假设与观点是基于笔者对模型及数据的一孔之见,若有不同见解欢迎随时留言交流;
3:笔者原则是只做干货的分享,后续将更新更多内容,但工作学习之余的闲暇时间有限,更新速度慢还请谅解;
4:本文主要数据通过数据爬虫获取,模型实现基于python3.8;
目录
1. 单一目标优化
2. 多目标规划求解
2.1 分散指标计算
2.2 均值-方差分散度最优化
3. 代码实现
4. 往期精选
1. 单目标优化
一个经典的均值方差最优化会形成最小方差前沿,以简单的两资产组合为例,组合回报率为:
组合标准差为:
通过随机权重,设计约束条件即可得到图一,最左侧的点连线即可得到最小方差前沿。
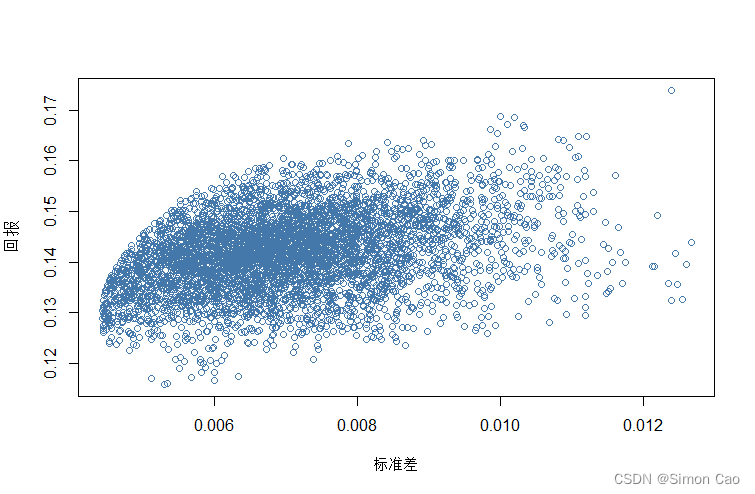
图一:一个均值方差最优化案例
对于均值方差最优化来说,标准差被看作是代表风险的指标。在不考虑客户效用曲线的前提下,其最优化目标即使得sharpe比率最大化,即是与前沿相切时的CAL(Capital Allocation Line)线,其切点处的投资组合夏普比率最大。
2. 多目标规划求解
标准差作为二阶矩,其实只能算是风险的其中一个方面,在上述最优化求解过程中,无法同时在多目标上进行优化。为了改进优化目标单一的缺点,笔者在均值方差最优化的基础上再引入其它维度,下面以组合分散度DR(Diversification Ratio)为例。
2.1 分散指标计算
首先这里的分散度并不是指投资组合里的证券数量,而是成分证券的相关性。
其中:为权重矩阵;
为成分证券的方差矩阵;
为组合协方差矩阵。
该式分母即是原始的投资组合方差计算公式,分子是不考虑协方差影响的组合方差。分子其实是投资组合处于最分散(理想状态)状态,即此时所有成分证券之间的相关性为0。当DR等于1时,意味着当前投资组合(分母)达到最分散的状态(分子)。
这个式子和有效前沿有类似的特征,设计优化目标[4]和约束条件[5]:
进行最优化后也可以得到类似均值方差最优化的一条有效前沿。
2.2 均值-方差分散度最优化
由于多加了一个维度,即是将原本的二维散点图延展到三维空间。因为三维空间没有斜率这个概念,原本的求解方案就无法使用单一的某个指标进行最优化了。不过三维空间还是可以通过偏导数求解出一个类似二维空间斜率的东西。
将Z轴设为投资回报率,那么最优组合一定是过无风险利率点,作与有效面相切的切线。由于无风险利率这个z轴上的点已经固定了,剩下只要求解x和y两个方向上的偏导数,使得过无风险利率点的两个方向上偏导达到最大即可完成目标。
另设x轴为标准差,y轴为分散度除以1(集中程度),CAL线方程为[6]式:
目标函数即是[7]式,线性约束条件依然满足[5]:
求解可以说非常的简单,不过这个式子其实并不是严格意义上的偏导数,因为z方向的偏导数是没有考虑进去的,笔者姑且管它叫“部分偏导”吧。
笔者选取4支私募基金进行最优化求解后得到三维散点分布及最优组合如图二。从图二不难看出,最优化组合所处位置其实并不在最顶端,也不在x和y方向投影的有效前沿上。这个组合除了进行均值方差最优还同时兼顾了一定的分散性,具备一定分散性的同时兼顾一定的风险回报最优,这就是多目标规划求解的优势。

图二:三维可视化
当然,通过这个思路还可以将分散度替换为其它指标,甚至加入更多指标,只是更高维的可视化就很难实现了。但是也需要注意指标也许不是越多越好,用绝大多数指标的不规则散点分布进行最优化得到的解很可能没有多大意义。
3. 代码实现
由于需要生成很多随机数和三维可视化,笔者借助R语言进行实现。笔者选取4支私募基金17年-20年的月度回报率数据,首先查看几个产品的相关性矩阵:
data <- data.frame(fund1$`涨跌幅(%)`, fund2$`涨跌幅(%)`, fund3$`涨跌幅(%)`, fund4$`涨跌幅(%)`)
names(data) <- c("基金1", "基金2", "基金3", "基金4")
cor(data)
col <- colorRampPalette(c("#BB4444", "#EE9988", "#FFFFFF", "#77AADD", "#4477AA"))
corrplot(cor(data), method = "shade", shade.col = NA, tl.col = "black", tl.srt = 0, col = col(200), addCoef.col = "black", cl.pos = NULL, order = "AOE", mar=c(1,1,1,2))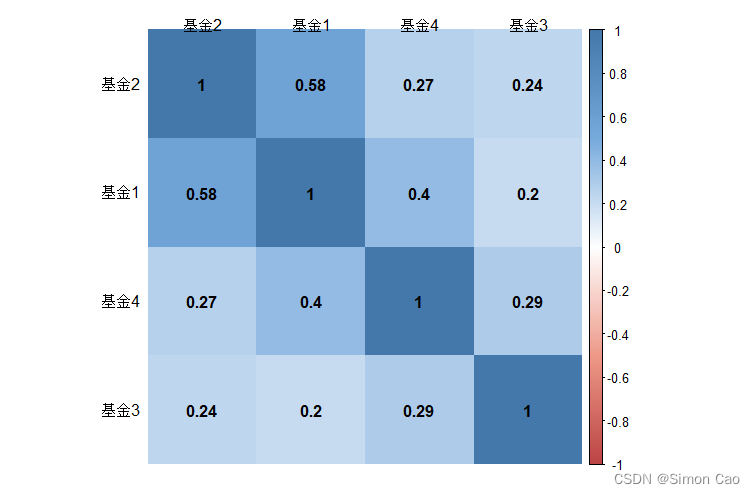
图三:组合相关性矩阵
下面进行最优化求解:
train_data <- data
train_data_nav <- cumprod(train_data)
r <- (train_data_nav[nrow(train_data_nav),] - train_data_nav[1,]) / train_data_nav[1,]
r <- (1 + r) ^ (12 / nrow(train_data_nav))-1 # 私募基金数据是月度的,要年化一下
r_matrix <- matrix(r, 1, 4) # 生成回报率矩阵
cov_matrix <- matrix(cov(train_data), 4, 4) # 生成协方差矩阵
std_cols <- apply(train_data, 2, sd) # 生成方差矩阵# 存储随机投资组合数据
w_lst <- list()
r_lst <- c()
std_lst <- c()
DR_lst <- c()
for (i in 1:5000){ # 5000次随机w <- runif(4,0,1) # 随机数生成w <- matrix(w/sum(w), 1, 4) # 归一化,变成矩阵std <- sqrt(w %*% cov_matrix %*% t(w))r_portfolio <- sum(r * w)dr <- std / sum(std_cols * w)DR_lst <- c(DR_lst, dr)w_lst[[i]] <- wr_lst <- c(r_lst, r_portfolio)std_lst <- c(std_lst, std)
}mvo <- data.frame(DR_lst, std_lst, r_lst)# 下面计算出多维MVO
mvo$r_lst <- mvo$r_lst - 0.024 # 无风险利率取2.4%
mvo$sharp <- mvo$r_lst / mvo$std_lst
mvo$diverfication <- mvo$r_lst / mvo$DR_lst
mvo$max_target <- mvo$sharp + mvo$diverfication # 两个方向的偏导数相加# 便历一下,查找最优化的权重配置
for (i in 1:nrow(mvo)){if (mvo$max_target[i] >= max(mvo$max_target)){print(i) # 第i个w_max <- w_lst[i]r_max <- r_lst[i]std_min <- std_lst[i]DR_min <- DR_lst[i]}
}cal_line <- data.frame(a = c(0, std_min*2), b = c(0, DR_min*2), c = c(0.024, r_max*2-0.024)) # 资产配置线的坐标
optimal_point <- data.frame(a = std_min, b = DR_min, c = r_max) # 最优组合的坐标最后通过plotly可视化即可获得炫酷的交互式三维图。
library(plotly)plot <- plot_ly() # 添加三维图
plot <- plot %>% add_trace(data = mvo, x = std_lst, y = DR_lst, z = r_lst, type = "scatter3d", size = 0.01, mode = "markers", name="投资组合")
plot <- plot %>% add_trace(data = cal_line, x = ~a, y = ~b, z = ~c, type = "scatter3d", mode = "lines", name = "资产配置线", showlegend = TRUE)
plot <- plot %>% add_trace(data = optimal_point, x = ~a, y = ~b, z = ~c, type = "scatter3d", size = 0.05, mode = "markers", marker = list(color="red"), name = "最优组合", showlegend = TRUE)
plot <- plot %>% # 添加标签和修改格式layout(scene = list(yaxis = list(title = "集中度", zeroline = TRUE, zerolinecolor = "black", range = c(0.5,1)),xaxis = list(title = "风险", zeroline = TRUE, zerolinecolor = "black", range = c(0,0.01)),zaxis = list(title = "回报", zeroline = TRUE, zerolinecolor = "black", range = c(0.1,0.2))),margin = list (1,1,1,1),legend = list(x=0.1, y = 0.9))print(plot)4. 往期精选
| 往期精选 | ||
| 系列 | 文章传送门 | 实现方式 |
| 金融杂谈 | 基于均值方差最优化资产配置的模型特性 | Python |
| 基金市场的冷热传递什么信号? | Python | |
| 券商金股哪家强——信息比率 | Python | |
| 从指数构建原理看待A股的三千点魔咒 | Python | |
| 决策树学习基金持仓并识别公司风格类型 | R | |
| 垃圾公司对回报率计算的影响几何 | Python | |
| 市场预测美联储加息的有效性几何 | Python | |
| 市场风险分析 | Python | |
相关文章:

多目标最优化的资产配置
摘要及声明 1:本文主要对基于均值方差最优化的资产配置方法进行拓展,从多目标最优化的角度看待资产配置并可视化展示; 2:本文主要为理念的讲解,模型也是笔者自建,文中假设与观点是基于笔者对模型及数据的…...
word图片的标题跑到了图片的上方。
问题描述:在写论文时,在word文档中插入了一个svg图片,然后在图片下方输入标题。后面可能是调整了svg图片的大小,标题跑到了图片的上方。 具体情况如下图所示。标题明显跑到了图片的上方。 解决办法:把svg图片格式调成…...

electron打包下载资源失败,设置国内镜像
0.electron介绍 Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 嵌入 Chromium 和 Node.js 到 二进制的 Electron 允许您保持一个 JavaScript 代码代码库并创建 在Windows、Linux及macOS上运行的跨平台应用。可以用原生html写,也可以用vue等…...

架构漫谈 - 如何设计高性能、高可用、高扩展架构
文章目录 一、如何设计高扩展架构架构设计复杂度模型可扩展复杂度模型"拆分"复杂度分析和设计"封装"复杂度分析和设计(1)规则引擎:美团MazeGO规则引擎(2)微内核:OSGI微内核(3)抽象层:Linux VFS抽象层(4)设计模式二、设计高性能架构单机高性能集…...
matlab 读写ENVI标准数据
本博客主要讲解如何读、生成ENVI标准格式的数据。主要分为四部分:读取ENVI头文件、读取ENVI数据、写入ENVI头文件、生成ENVI标准数据,最后附加讲解了本人写的生成hdr文本文件代码。此外,文中还具体介绍写代码的一些思路。 一、读取ENVI头文件…...
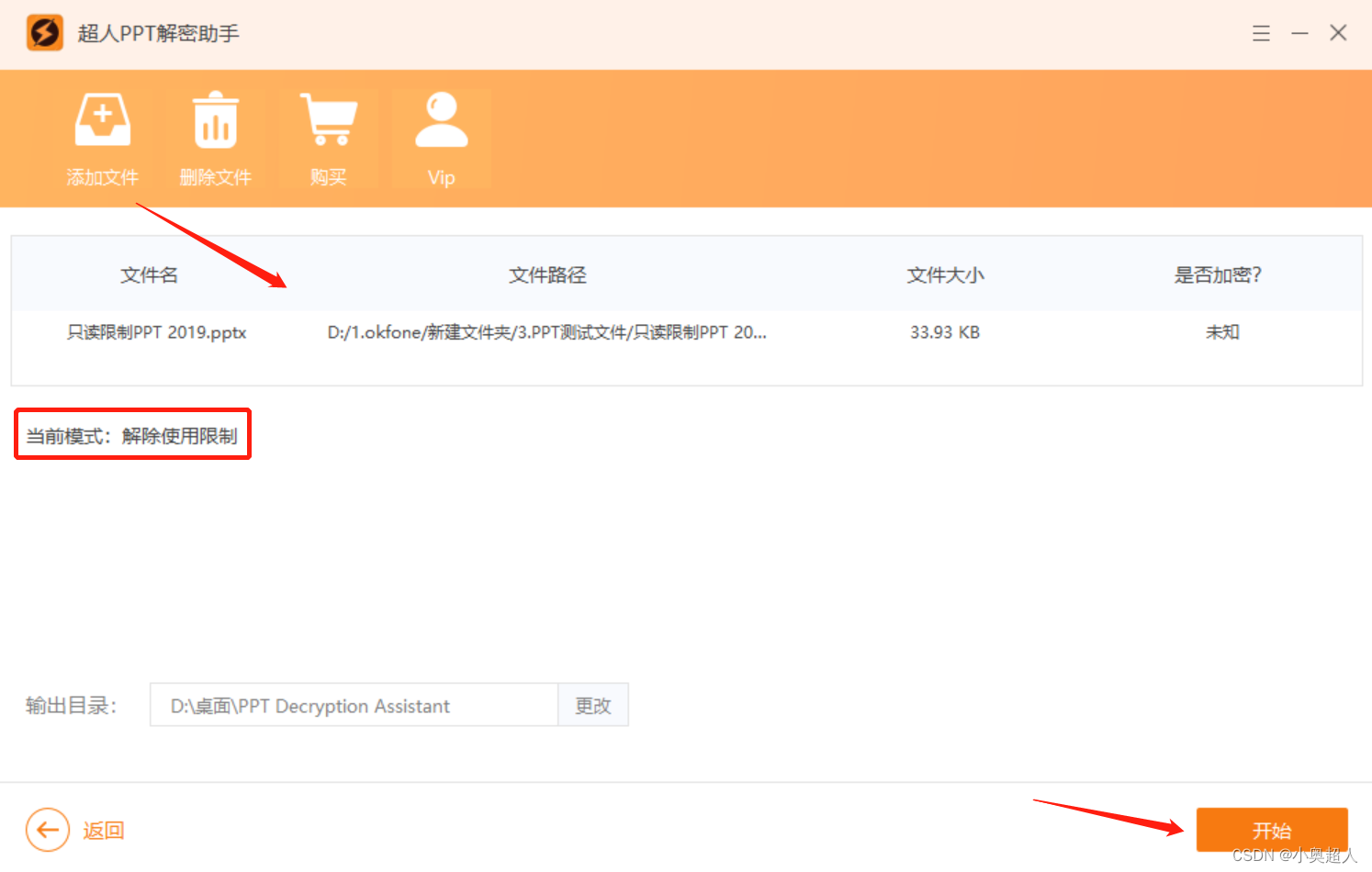
如何对ppt文件设置修改权限?
PPT文件会应用在会议、演讲、课件等工作生活中,当我们制作好了PPT之后,保护内容防止在演示时出错是很重要的,那么如何将PPT文件设置成禁止修改模式呢?今天分享几个方法给大家。 方法一 将PPT文件直接保存或者另存为一份文件&…...

STM32G030F6P6 芯片实验 (二)
STM32G030F6P6 芯片实验 (二) Hello World - GPIO LED 尝试了下, 从 0 开始建 MDK HAL M0plus Project, 成功点亮 LED了。 但是 ST-LINK跑着跑着, 码飞了! 不知飞哪去了。 只好拿 MX 建了个 MDK Base。 呼叫 SysTick HAL_Delay(), 切换 LED。 基本上都是一样的用法, 只是换…...

时间序列预测模型实战案例(七)(TPA-LSTM)结合TPA注意力机制的LSTM实现多元预测
论文地址->TPA-LSTM论文地址 项目地址-> TPA-LSTM时间序列预测实战案例 本文介绍 本文通过实战案例讲解TPA-LSTM实现多元时间序列预测,在本文中所提到的TPA和LSTM分别是注意力机制和深度学习模型,通过将其结合到一起实现时间序列的预测,本文利用…...

Mysql多表设计
前言 多表查询中要给每一表起别名 tableA as 别名1 , tableB as 别名2 ; (111111推荐) tableA 别名1 , tableB 别名2 ; 例子: select emp.name , dept.name from tb_emp emp inner join tb_dept dept on emp.dept_id dept.id; 一对一 在任…...
)
第九章:最新版零基础学习 PYTHON 教程—Python 元组(第五节 -清除元组的5种方式方法)
有时,在处理记录数据时,我们可能会遇到需要执行数据记录清除的问题。元组是不可变的,无法修改,因此使这项工作变得困难。让我们讨论执行此任务的某些方法。 目录 方法 #1:使用 list() + clear() + tuple() 方法#2:使用 tuple() 重新初始化...

学习笔记4——JVM运行时数据区梳理
学习笔记系列开头惯例发布一些寻亲消息 链接:https://baobeihuijia.com/bbhj/contents/3/192489.html 类装载器classLoader: 将本地的字节码文件.class 加载到内存方法区中成为元数据模板(两个class对象是否为同一个类要求:完整…...
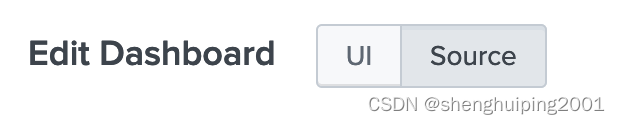
Splunk 创建特色 dashboard 报表
1: 背景: 对原有的dashboard 进行增加点东西,特别是文字部分: 比如: 增加:“this is a guidline for how to use performance". 这段话,就不能写在title, 那样,这段文字,会出现在dashboard 的PDF 文件的分割线的上面,不符合要求。 2: 解决问题: 正确的做法是…...

如何在校园跑腿系统小程序中构建稳健的订单处理与分配系统?
1. 数据库设计 首先,设计订单数据结构。使用数据库(例如MySQL、MongoDB等),创建订单表以存储订单相关信息,包括订单ID、用户信息、交付地址、订单状态等。 CREATE TABLE orders (order_id INT AUTO_INCREMENT PRIMAR…...
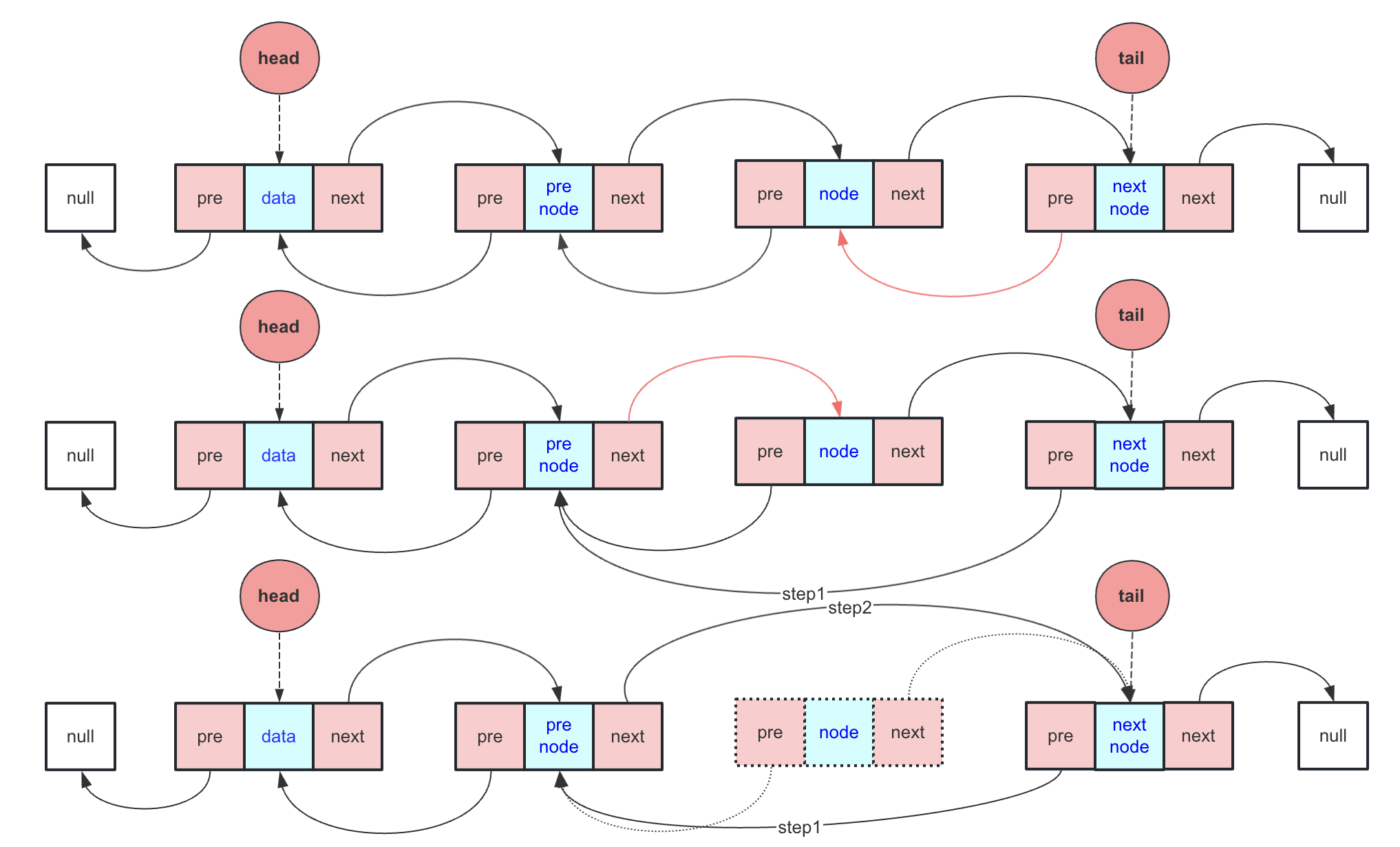
数据结构与算法—双链表
前言 前面有很详细的讲过线性表(顺序表和链表),当时讲的链表以单链表为主,但在实际应用中双链表有很多应用场景,例如大家熟知的LinkedList。 双链表与单链表区别 单链表和双链表都是线性表的链式实现,它们的主要区别在于节点结构…...
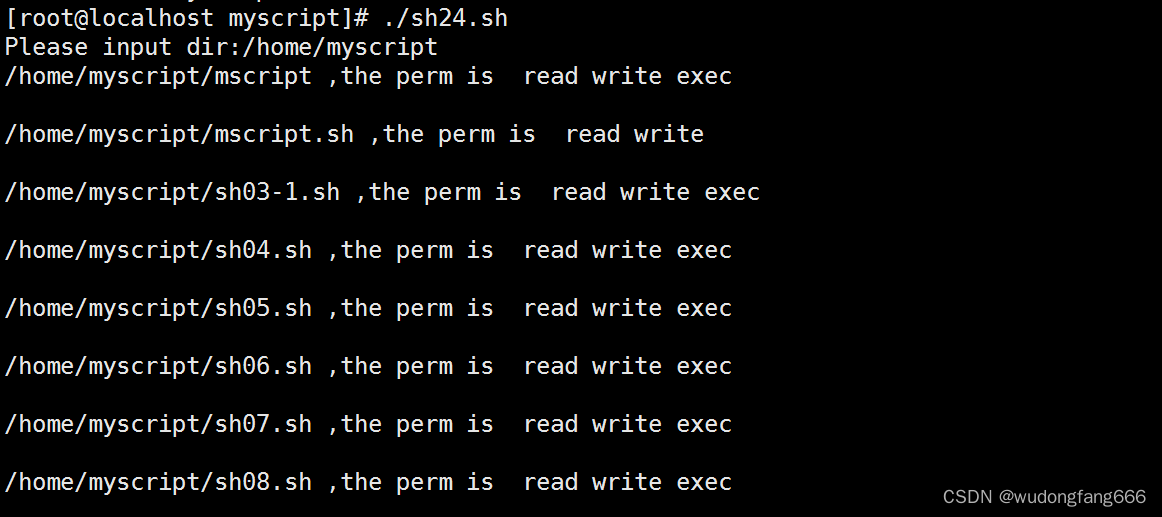
linux继续循环案例测试ping网络,目录下的文件权限循环输出
第一:查看本机ip #ip addr 通过脚本访问本机ip1-100,是否可以ping通,并显示结果,上图 知识点 ping -c 数字1 -w 数字1,向目的ip发送1个数据包,等待1秒,无回复中止 &>/dev/null 知…...
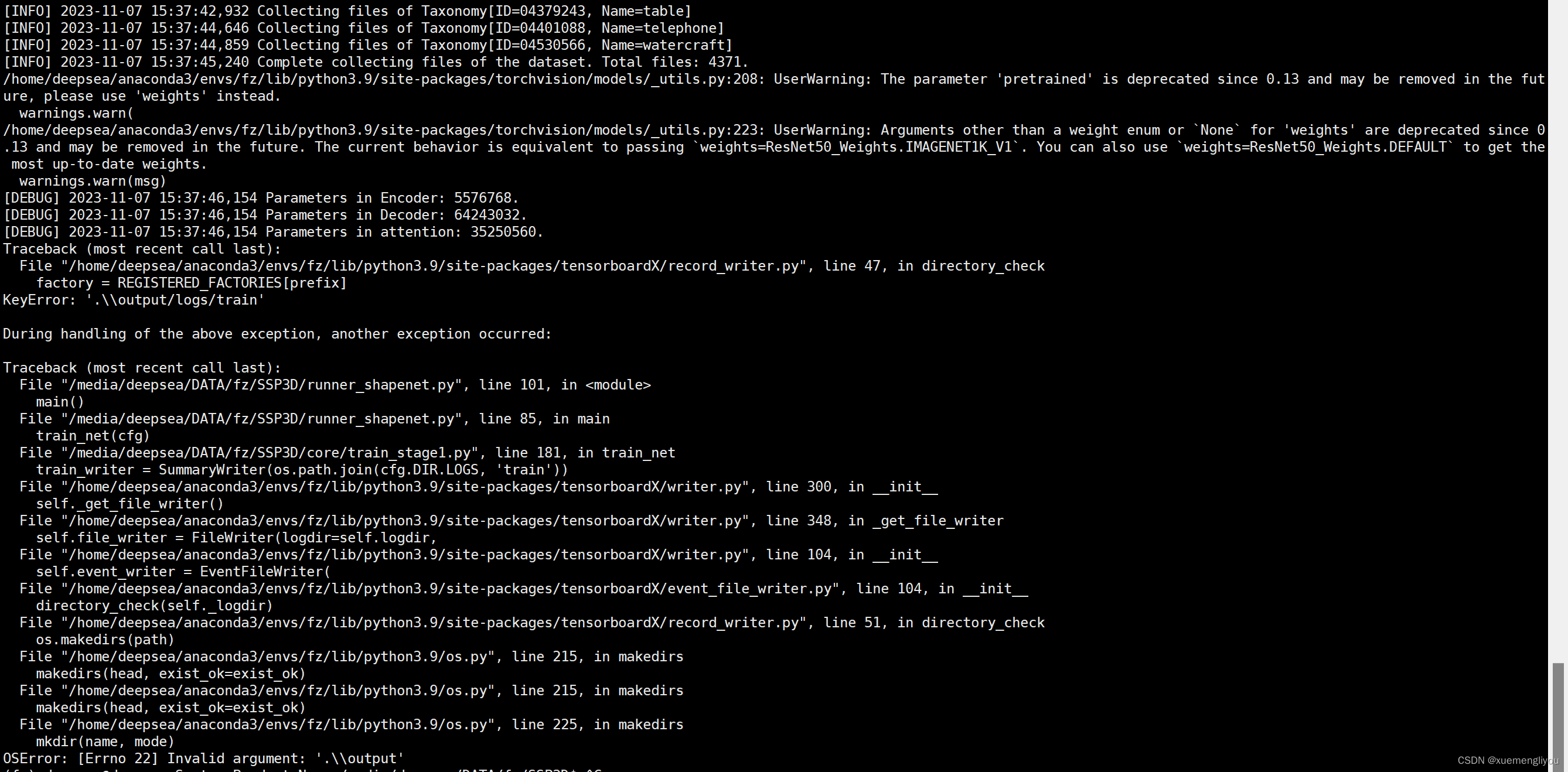
关于SSP3D复现
关于SSP3D复现的问题 准备工作 下载Xshell和XFTP:家校免费版下载链接连接服务器(可能需要与服务器处在相同网络下)GitHub上下载源码:SSP3D 左上角新建会话,输入名称和主机 点击左侧菜单“用户身份验证”,…...
在直播系统中使用RTSP协议传递视频
目录 概述 1、环境准备 2、拉流URL地址 3、导播软件取流 (1)OBS中拉取RTSP流 (2)芯象中拉取RTSP流 (3)vMix中拉取RTSP流 写在最后 概述 提到RTSP协议,很容易想到RTMP协议,它…...
Notion汉化
Notion真无语,汉化版都没有。真的无力吐槽。 2023.11.7汉化经历 教程链接:github Reamd7/notion-zh_CN at 2.4.20-handmade (github.com) 网页版: 油猴下载插件。 Notion中文汉化 浏览器插件下载 windows: github realse 这…...

echarts有背景的柱状图,鼠标滑过提示信息都是展示背景柱状图的值
// 上一篇文章介绍了如何实现有背景的柱状图,现在又遇到一个问题,鼠标滑过柱子,提示信息是背景柱子的值,解决方案,自定义tooltip的formatter,上代码tooltip: {//鼠标悬浮提示数据formatter: function (para…...

华为防火墙基本原理工作方法总结
防火墙只会对tcp首包syn建立会话表,其它丢掉,如synack,ack udp直接建立会话表 icmp只对首包请求包建立会话表,其它包,如应答的不会建立直接丢掉 防火墙状态查看: rule name trust_untrust source-zone tru…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
