基于人工蜂鸟算法的无人机航迹规划-附代码
基于人工蜂鸟算法的无人机航迹规划
文章目录
- 基于人工蜂鸟算法的无人机航迹规划
- 1.人工蜂鸟搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用人工蜂鸟算法来优化无人机航迹规划。
1.人工蜂鸟搜索算法
人工蜂鸟算法原理请参考:https://blog.csdn.net/u011835903/article/details/128386612
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得人工蜂鸟搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用人工蜂鸟算法对航迹评价函数式(7)进行优化。优化结果如下:


从结果来看,人工蜂鸟算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于人工蜂鸟算法的无人机航迹规划-附代码
基于人工蜂鸟算法的无人机航迹规划 文章目录 基于人工蜂鸟算法的无人机航迹规划1.人工蜂鸟搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用人工蜂鸟算法来优化无人机航迹规划。 …...

51单片机汇编-点亮一个led
文章目录 前言1.打开IDE2.设置编辑器3.设置输出4. 原理图5.编写代码6 编译7.下载8.其它代码1.LED闪烁2.跑马灯 前言 51单片机基础 51汇编实战 本章主要介绍打开一个led,具体采用51汇编 1.打开IDE 选择STC89C52RC 后缀是.asm 2.设置编辑器 3.设置输出 4. 原理图 5.编写代码 …...

每天一点python——day62
为了方便复制,我在下面附带了一个python文件。 C:\Users\Admin>python Python 3.9.13 (main, Aug 25 2022, 23:51:50) [MSC v.1916 64 bit (AMD64)] :: Anaconda, Inc. on win32Warning: This Python interpreter is in a conda environment, but the environmen…...
基于SSM的智慧作业试题管理系统(有报告)。Javaee项目。
演示视频: 基于SSM的智慧作业试题管理系统(有报告)。Javaee项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构,通过Spring Sprin…...
ESP32 未来能够取代 STM32吗?
今日话题,ESP32 未来能够取代 STM32吗?ESP32和STM32各自有其特点和优势,能否取代彼此取决于具体应用和需求。STM32的流行除了性价比外,还有其强大的开发环境,例如Cubemx能够快速生成代码,使得上手STM32的速…...
Java连接Redis并操作Redis中的常见数据类型
目录 一. Java连接Redis 1. 导入依赖 2. 建立连接 二. Java操作Redis的常见数据类型存储 1. Redis字符串(String) 2. Redis哈希(Hash) 3. Redis列表(List) 4. Redis集合(Set) 一. Java连接Redis 1. 导入依赖 pom依赖…...

Python 基于分位数-正态分布转换的评分算法
在实验的时候遇到一个比较实际的问题,就是怎样对数据进行评分。比如我想根据样本的正确率进行打分,有两种方法,一种是将准确率排序,然后根据序号进行打分,这样可以排除极端数据的影响,但是准确率之间的差距…...

如何修改CentOS登录时默认目录
查了一下,有说改/etc/passwd文件的,有说改.bashrc文件的,也有说改.bash_profile,修改的方法都不一样。 我要改的是root登录时的目录,最后修改了/root/.bash_profile文件,只要加一行cd 路径就可以。 这个文…...

JavaFX Scene Builder Gluon 控件详解
在 JavaFX Scene Builder 工具中,Gluon 是一个扩展库,提供了一些额外的控件和功能,用于创建更丰富和现代化的用户界面。本文将详细介绍 Gluon 中的各个控件及其作用。 AppBar(应用栏) AppBar 是一个用于显示应用程序…...

Vue路由(router-link)——高亮、动态传参
一、声明式导航-导航链接 1.需求 实现导航高亮效果 如果使用a标签进行跳转的话,需要给当前跳转的导航加样式,同时要移除上一个a标签的样式,太麻烦!!! 2.解决方案 vue-router 提供了一个全局组件 router…...

Java中将List转换为Map
在Java 8中,Stream API和Collectors类提供了一种方便的方式来处理集合数据。其中,将List转换为Map是一个常见的操作。下面我们将介绍如何使用Stream API和Collectors类将List转换为Map。 首先,假设我们有一个User类,包含id和name两…...
进程控制2——进程等待
在上一小节中我们介绍了进程的创建(fork)与退出(main函数的return与exit函数) 并且要有一个意识,进程退出的时候只有三种情况: 1.进程退出,结果正确 2.进程退出,结果不正确 3.运行异…...
k8s service
文章目录 Service 基础概念Service 类型:Service 的工作流程:东西流量,南北流量NodePortLoadBalancer Service 基础概念 在 Kubernetes(K8s)中,Service 是一个抽象的概念,表示一个应用程序的逻…...
C语言 每日一题 PTA 11.6 day12
1.调和平均 N 个正数的算数平均是这些数的和除以 N,它们的调和平均是它们倒数的算数平均的倒数。 本题就请你计算给定的一系列正数的调和平均值。 输入格式: 每个输入包含 1 个测试用例。每个测试用例第 1 行给出正整数 N(≤1000);第 2 行给…...
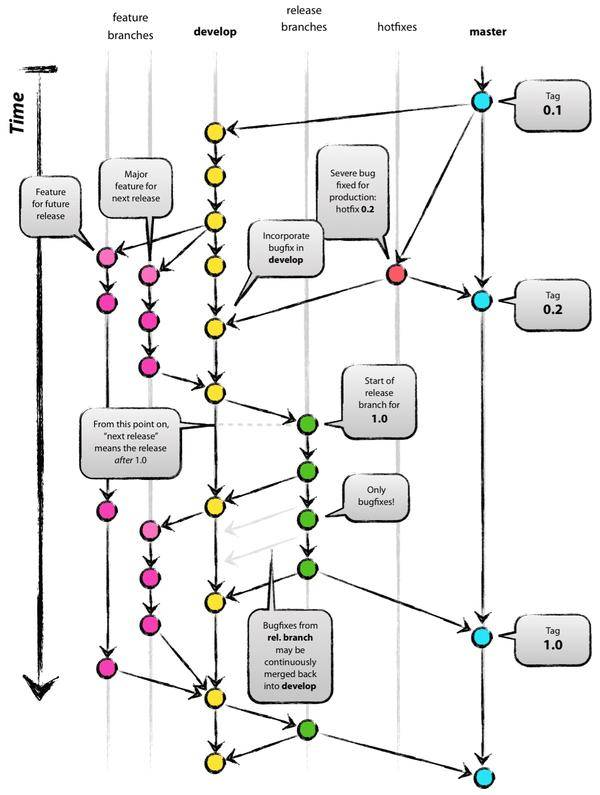
Git使用规范指南
文章目录 Git使用规范指南前言分支命名规范分支合并流程规范提交信息规范Angular提交规范注意事项 通用Git忽略文件配置 Git使用规范指南 前言 由于最近写完代码之后,Git使用不规范被领导说了,所以最近通过阅读大量的相关博客快速学习Git使用规范&#…...

axios和Ajax
1.axios 官网:https://axios-http.com/zh/ CDN:https://cdn.bootcdn.net/ajax/libs/axios/0.21.1/axios.min.js axios是一个请求库,在浏览器环境中,它封装了XHR,提供更加便捷的API发送请求 基本使用 // 发送 get 请求…...

Day06
1.继承 1.1 定义 让类与类之间产生子父类关系,有了继承性之后,子类就获取到了父类中声明的所有属性和方法。 1.2 优点 继承的出现减少了代码冗余,提高了代码的复用性。继承的出现,更有利于功能的扩展。继承的出现让类与类之间…...
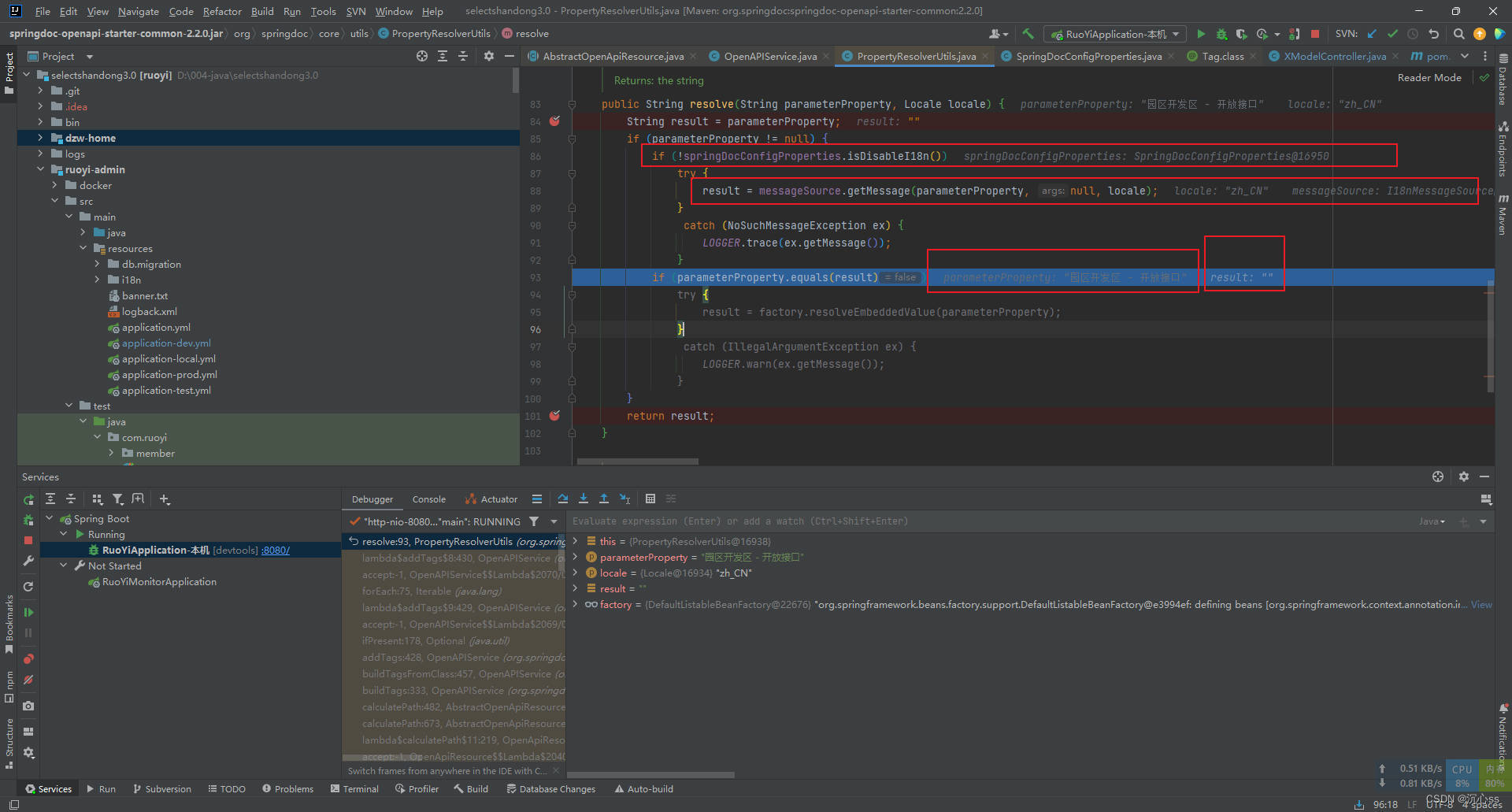
@Tag和@Operation标签失效问题。SpringDoc 2.2.0(OpenApi 3)和Spring Boot 3.1.1集成
问题 Tag和Operation标签失效 但是Schema标签有效 pom依赖 <!-- 接口文档--><!--引入openapi支持--><dependency><groupId>org.springdoc</groupId><artifactId>springdoc-openapi-starter-webmvc-ui</artifactId><vers…...
基础课18——智能客服系统架构
1.基础设施层 基础设施主要包括以下几点: 1. 硬件设施:包括服务器、存储设备、网络设备等,这是整个系统运行的物理基础。 2. 软件设施:包括操作系统、数据库管理系统、自然语言处理(NLP)工具和机器学习算法等,这些是…...

python执行cmd命令——控制电脑连接wifi——程序打包
import subprocess # 使用Popen创建进程,并与进程进行复杂的交互 proc subprocess.Popen(netsh wlan show network, # cmd特定的查询空间的命令stdinNone, # 标准输入 键盘stdoutsubprocess.PIPE, # -1 标准输出(演示器、终端) 保存到管道中以便进行操作…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
