【无标题】360压缩软件怎么用?超级好用!
360压缩是一款功能强大的解压缩软件,如何用它压缩文件呢?下面给出了详细的操作步骤。

一、360压缩详细步骤
1、下载软件后,在电脑上右击需要压缩的文件,在弹出的菜单中点击【添加到压缩文件】选项。
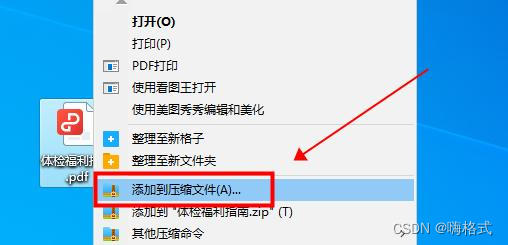
2、在360压缩窗口中按需设置相关参数,比如修改压缩文件名称、选择压缩配置等,如果需要给文件加密,就点击【添加密码】选项。

3、再在添加密码窗口输入并确认密码。
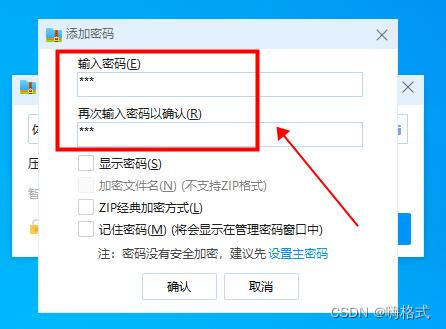
4、设置好以上内容后点击【立即压缩】按钮,软件就会压缩文件。
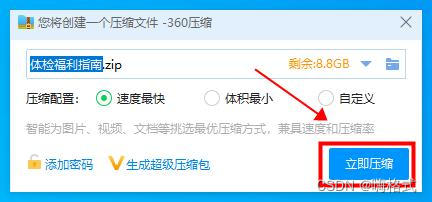
5、完成后文件就会自动生成一个压缩包,360压缩文件就完成啦。
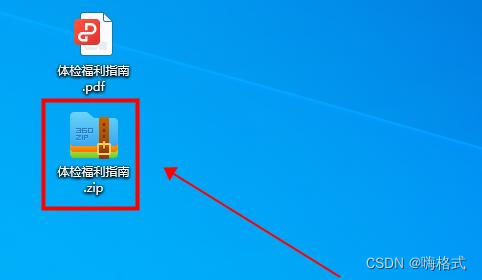
360压缩的界面较为复杂,对于一些新手用户来说可能会有一定的学习成本。
也可以使用下面这款简洁易用的压缩软件,支持批量压缩视频、图片、PDF、Word、PPT等多种文件,无广告,界面简洁,功能模块一目了然,小白也能轻松上手。此外,还支持多种模式的压缩,可以满足不同用户的需求。同时,还采用了最新离线压缩技术,压缩率高的同时保证文件安全。
二、嗨格式压缩大师操作步骤
1、打开软件,在主界面中点击“视频压缩”功能;
2、进入后点击“添加文件”添加视频,或直接通过拖拽的方式将视频导入到软件中;
3、视频添加完成后,根据不同的需要在右侧选择压缩模式,主要分为两种,一个是快捷设置,包含普通压缩、按清晰度优先压缩和极限压缩,另一个是高级设置,就可以按比特率或文件大小,自定义压缩参数;
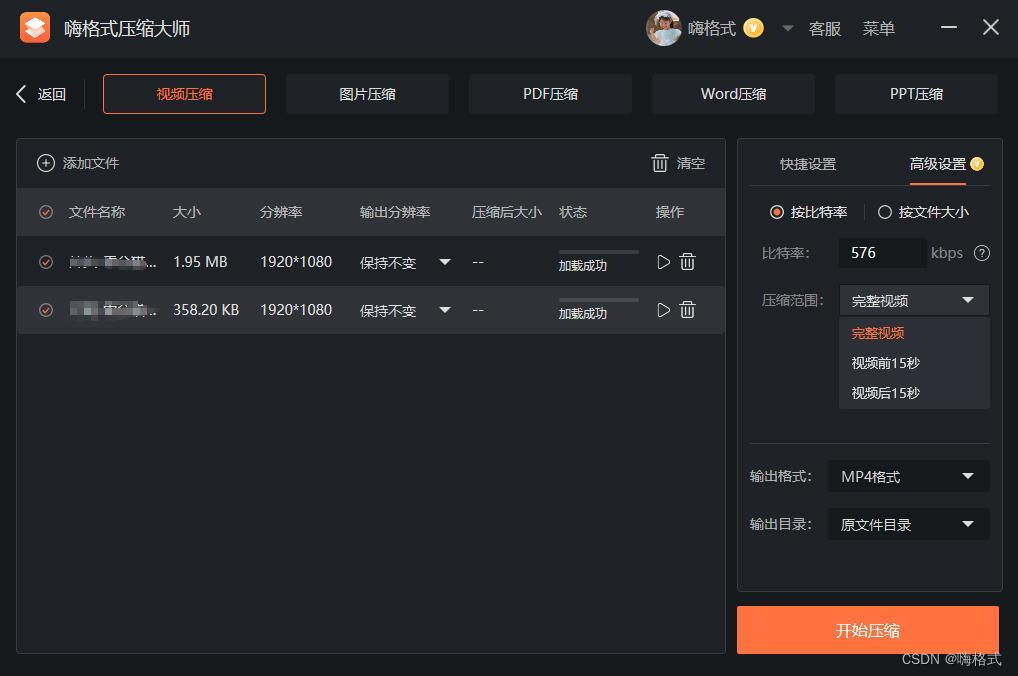
4、最后点击“开始压缩”按钮就可以完成视频压缩,在软件界面中也可以直接看出压缩前后的视频大小,很方便。
以上就是今天介绍的360压缩软件怎么用的方法,希望对大家有所帮助~
相关文章:

【无标题】360压缩软件怎么用?超级好用!
360压缩是一款功能强大的解压缩软件,如何用它压缩文件呢?下面给出了详细的操作步骤。 一、360压缩详细步骤 1、下载软件后,在电脑上右击需要压缩的文件,在弹出的菜单中点击【添加到压缩文件】选项。 2、在360压缩窗口中按需设置相…...
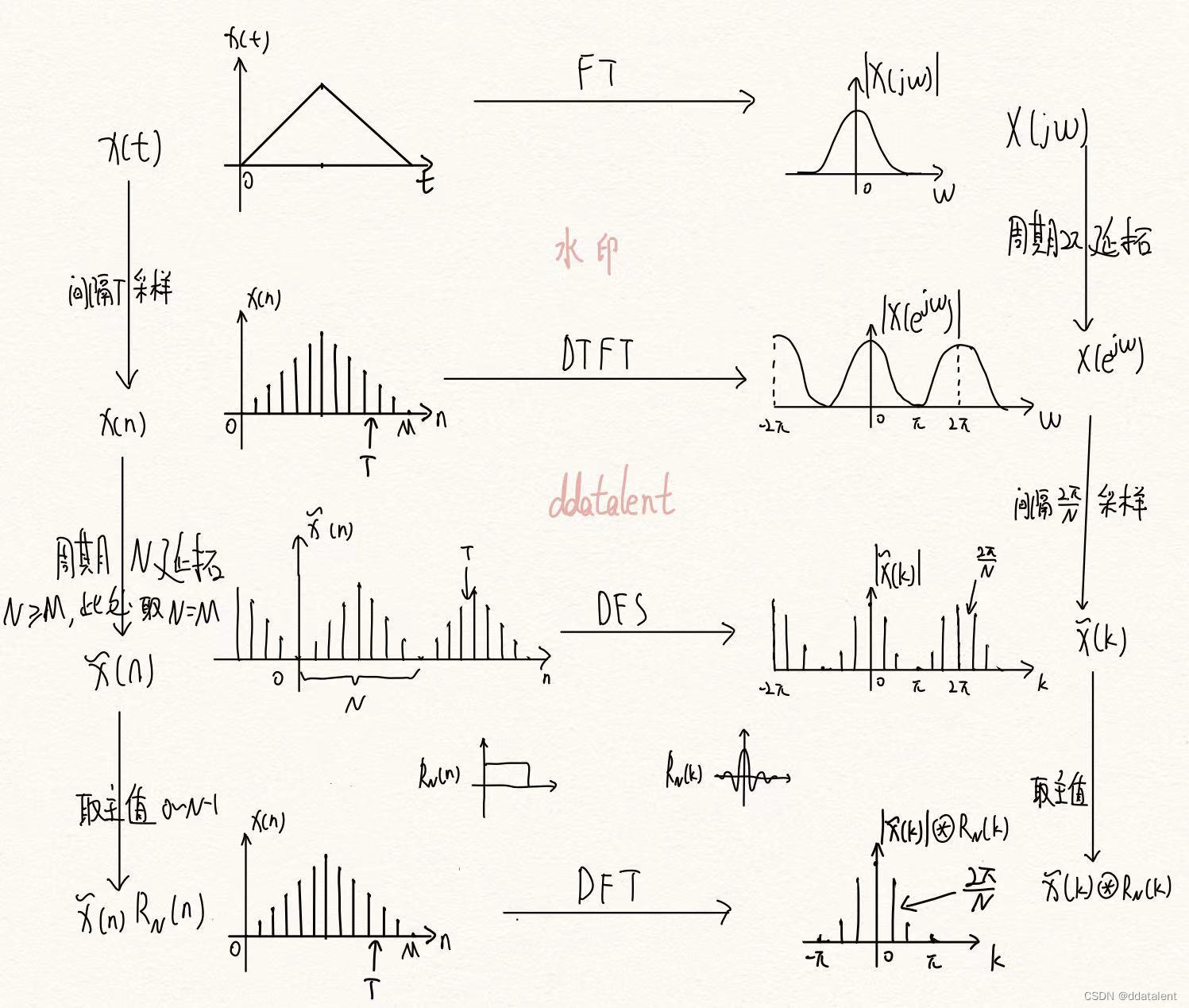
一图搞懂傅里叶变换(FT)、DTFT、DFS和DFT之间的关系
自然界中的信号都是模拟信号,计算机无法处理,因此我们会基于奈奎斯特定理对模拟信号采样得到数字信号。 但是我们发现,即便是经过采样,在时域上得到了数字信号,而在频域上还是连续信号。 因此我们可以在时域中选取N点…...
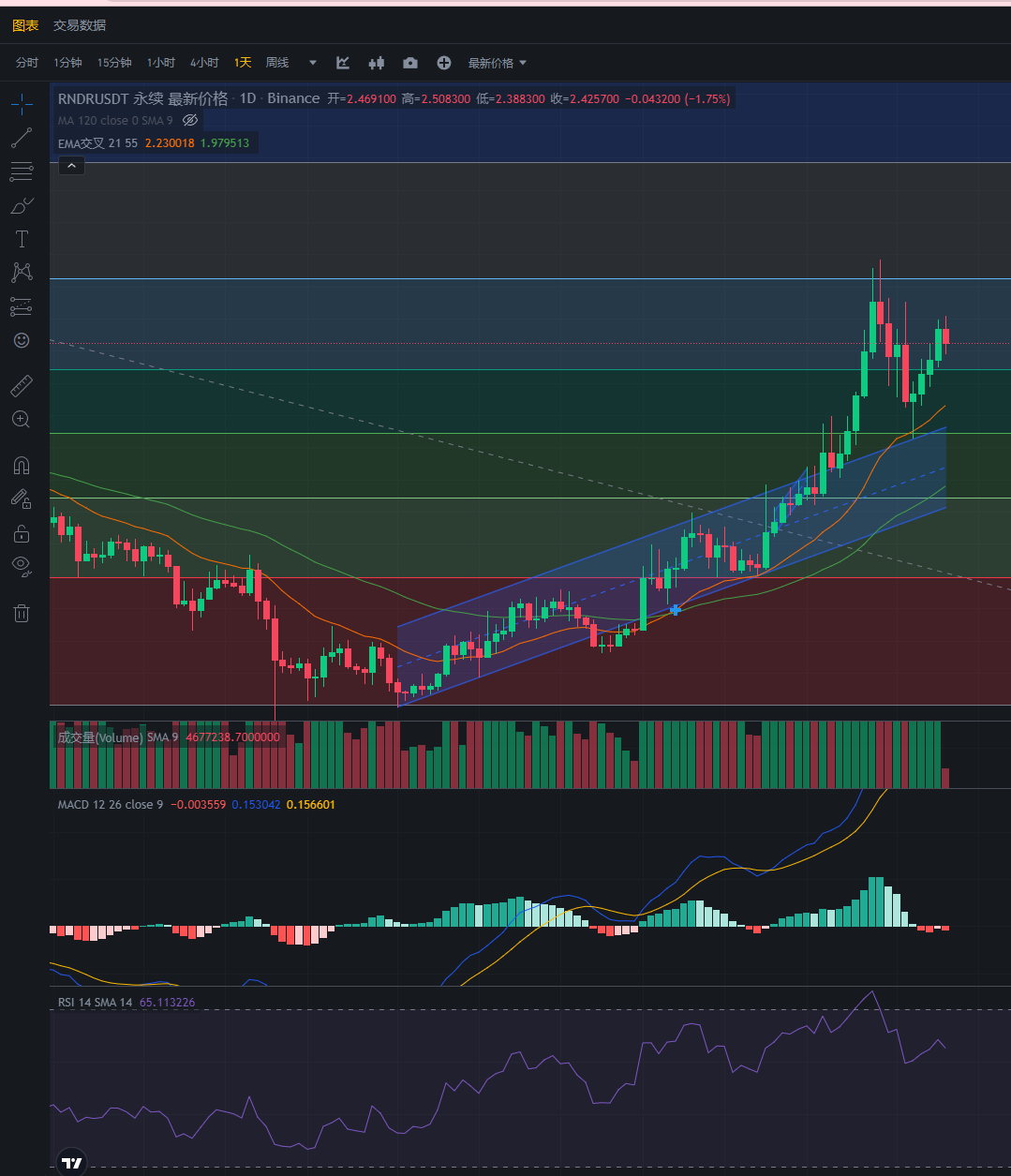
行情分析——加密货币市场大盘走势(11.7)
大饼昨日下跌过后开始有回调的迹象,现在还是在做指标修复,大饼的策略保持逢低做多。稳健的依然是不碰,目前涨不上去,跌不下来。 以太昨天给的策略,依然有效,现在以太坊开始回调。 目前来看,回踩…...
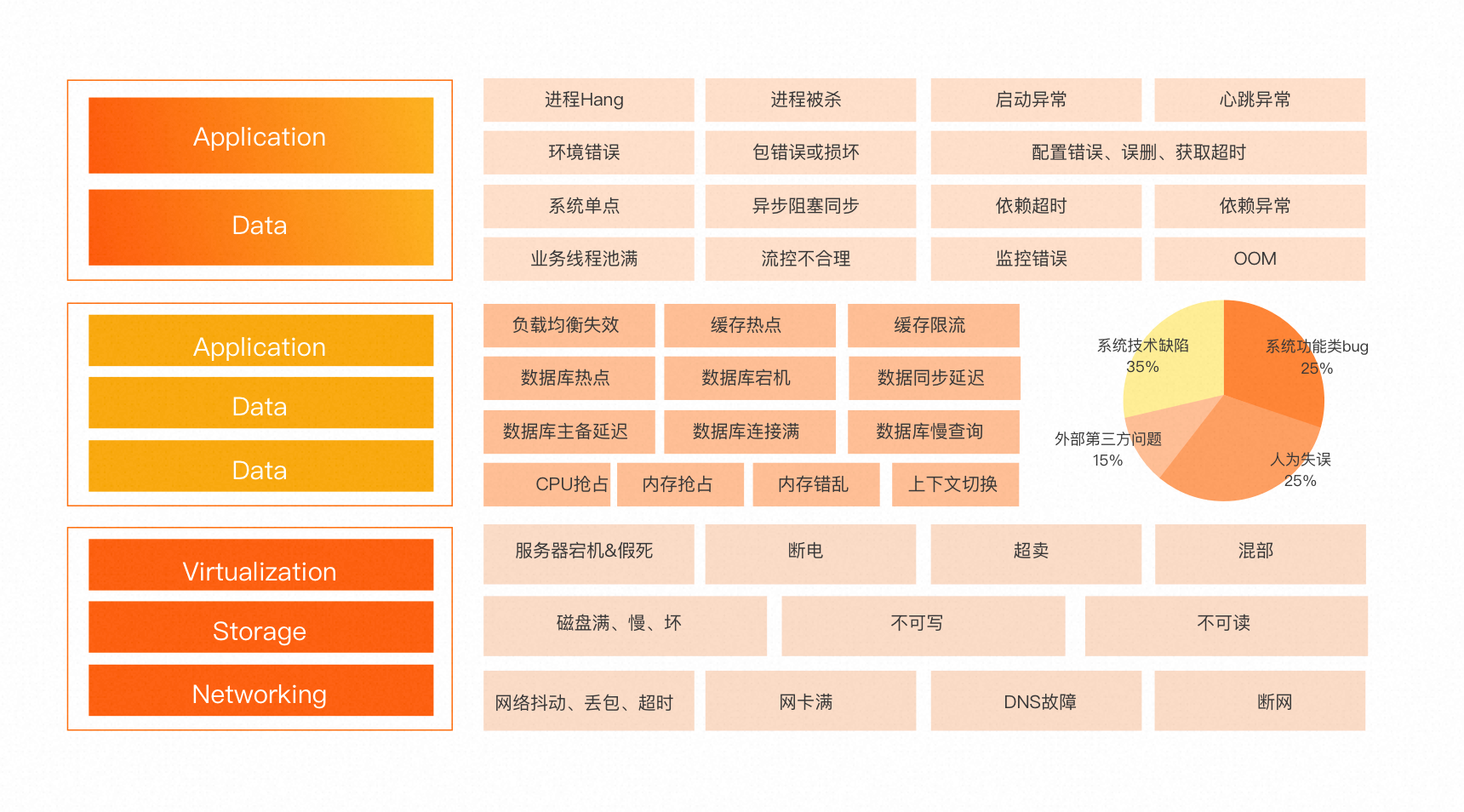
阿里微服务质量保障系列:故障演练
对于很多大型企业(如阿里巴巴)来说,经过多年的技术演进,系统工具和架构已经高度垂直化,服务器规模也达到了比较大的体量。当服务规模大于一定量(如10000台)时,小概率的硬件故障每天都会发生。这时如果需要人的干预,系统就无法可靠的伸缩。 为此每一层的系统都会面向失…...
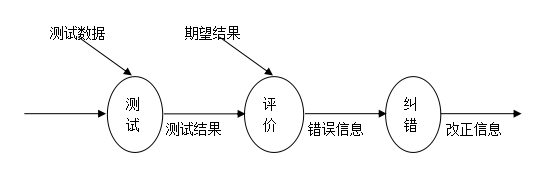
基于springboot+vue开发的教师工作量管理系
教师工作量管理系 springboot31 源码合集:www.yuque.com/mick-hanyi/javaweb 源码下载:博主私 摘要 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了教师工作量管理系统的开发全过程。通过…...

【NI-DAQmx入门】NI-DAQmx之C、C++、VB、VB.net与C#支持
DAQmx应用程序编程接口(API) DAQmx附带数据采集编程所需的API。DAQmx API只是一组库,其中包含关于如何执行所有数据采集操作的函数。这些API支持LabWindows/CVI、C、C、Visual Basic 6.0、VB.NET和C#。 DAQmx API随DAQmx驱动程序一起安装,包含以下参考…...

python转xml为json
以下代码取自获取PA防火墙策略XML文件并转为JSON文件的场景: 通过PA防火墙API获取防火墙策略 防火墙策略xpath为./result/security/rules/entry 以下代码实现将所有entry即策略与策略相关属性转为json对象并存储至文件 import xml.etree.ElementTree as ET import …...

PHP Curl请求封装
php 中curl请求模块封装 <?php namespace App\Utils;/*** http 工具类* author Administrator**/ class HttpUtils {private static $_instance;private function __construct(){}public static function getInstance(){if( null self::$_instance ){self::$_instance n…...

java list set 特性
List的常用实现类 ArrayList (常用) JDK1.2 底层数组实现 查询快,增删慢 线程不安全,效率高 LinkedList JDK1.2 底层链表实现 查询慢,增删快 线程不安全,效率高 Vector JDK1.0 底层数组实现 都慢 线程安全,效率低 List 集合名new 实现类(); 常用方法 集合名.方法名(实参列表…...

Docker 用centos 编译安装apache
Docker 用centos 编译安装apache 前提条件: 安装docker 如果想安装docker请查阅:安装docker 环境准备:centos8 拉取centos镜像 [rootlvs docker]# docker pull centos:8 8: Pulling from library/centos a1d0c7532777: Pull complete Di…...

专访虚拟人科技:如何利用 3DCAT 实时云渲染打造元宇宙空间
自古以来,人们对理想世界的探索从未停止,而最近元宇宙的热潮加速了这一步伐,带来了许多新的应用。作为元宇宙的关键入口,虚拟现实(VR)将成为连接虚拟和现实的桥梁。苹果发布的VISION PRO头戴设备将人们对VR…...
第三章:人工智能深度学习教程-基础神经网络(第二节-ANN 和 BNN 的区别)
在本文中,我们将了解单层感知器及其使用 TensorFlow 库在Python中的实现。神经网络的工作方式与我们的生物神经元的工作方式相同。 生物神经元的结构 生物神经元具有三个基本功能 接收外部信号。 处理信号并增强是否需要发送信息。 将信号传递给目标细胞&#x…...
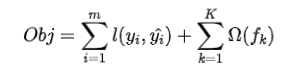
回归模型原理总结及代码实现
前言 本文将介绍回归模型算法,并总结了一些常用的除线性回归模型之外的模型,其中包括一些单模型及集成学习器。 保序回归、多项式回归、多输出回归、多输出K近邻回归、决策树回归、多输出决策树回归、AdaBoost回归、梯度提升决策树回归、人工神经网络、…...

游戏开发中的“御用中介“
点击上方亿元程序员关注和★星标 引言 大家好,我是亿元程序员,一位有着8年游戏行业经验的主程。 本系列是《和8年游戏主程一起学习设计模式》,让糟糕的代码在潜移默化中升华,欢迎大家关注分享收藏订阅。 游戏开发中的"御用…...

flink1.15报错 processElement_split
flink sql 完整报错 Caused by: java.lang.NullPointerExceptionat StreamExecCalc$1148.processElement_split178(Unknown Source) ~[?:?]at StreamExecCalc$1148.processElement(Unknown Source) ~[?:?]at org.apache.flink.streaming.runtime.tasks.CopyingChainingOutp…...

电脑投屏到TCL电视鼠标延迟
问题描述 提示:这里描述项目中遇到的问题: 笔记本电脑使用HDMI投屏到TCL电视,页面显示正常但是鼠标延迟反应太慢了 解决方案: 提示:这里填写该问题的具体解决方案: TCL电视设置中选择图像 → 图像类型改…...
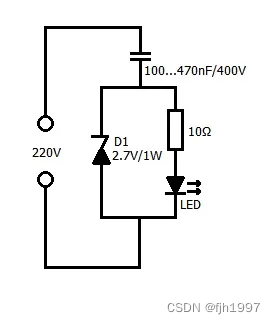
220v插座led指示灯维修
由于220v是交流电,有反向电压的情况,而led反向通电的时候电阻无穷大,所以分压也无穷大,220v一导通就击穿,即使加了很大的电阻也没用,串联电阻只能作用于二极管正向的时候。 目前有两种方案: 方…...
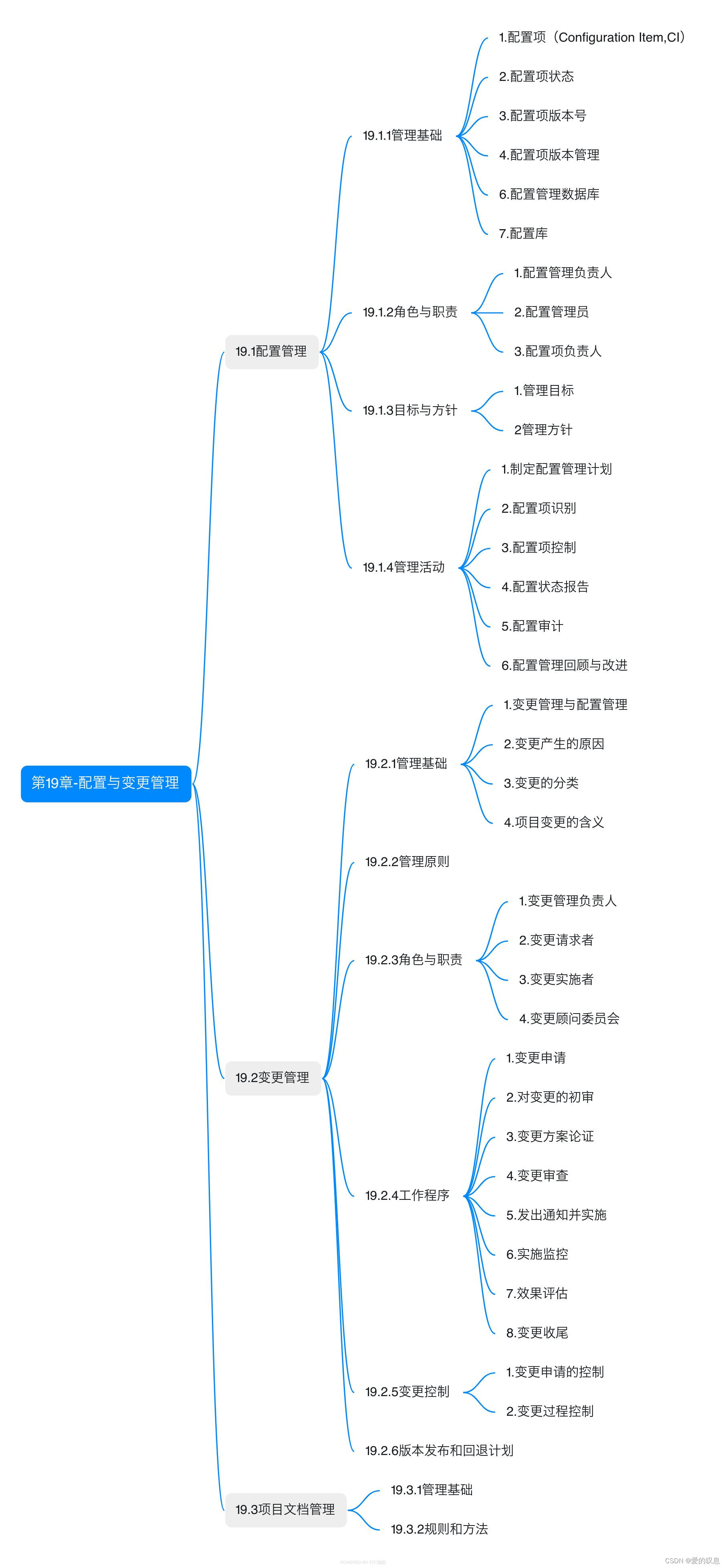
软考-高级-信息系统项目管理师教程 第四版【第19章-配置与变更管理-思维导图】
软考-高级-信息系统项目管理师教程 第四版【第19章-配置与变更管理-思维导图】 课本里章节里所有蓝色字体的思维导图...

javascript自定义事件的观察者模式写法和用法以及继承
<html><head><meta http-equiv"Context-Type:text/html;charsetutf-8"/><title>自定义事件之观察者模式</title><script type"text/javascript" src"common.js"></script></head><body>&…...
)
蓝桥杯官网练习题(正则问题)
题目描述 考虑一种简单的正则表达式: 只由 x ( ) | 组成的正则表达式。 小明想求出这个正则表达式能接受的最长字符串的长度。 例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是: xxxxxx,长度是 6。 输入描述 一个由 x()| 组成的正则表…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
