数据结构与算法C语言版学习笔记(2)-线性表、顺序存储结构的线性表
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 数据结构部分的知识框架
- 一、线性表的定义和特点
- 1.定义
- 2.特点
- 二、线性表的实际案例引入
- 1.案例一:多项式的加减乘除
- 2.案例二:当多项式是稀疏多项式时:
- ①稀疏多项式的定义:稀疏多项式(Sparse Polynomial)是指在多项式中,只有很少的系数是非零的情况下。具体地说,稀疏多项式是指多项式中的非零系数的数量远远小于总系数的数量。
- 3.案例三:图书管理系统
- 三、线性表的类型定义
- 1.
- 四、线性表的顺序表示和实现
- 类C语言中的一些说明
- 1.结构体嵌套
- 2.静态数组与动态数组
- 顺序表的示意图
- ①线性表的插入元素
- 五、顺序表的元素操作代码表达
- (1)查找(获得)第i个元素的值并返回该值GetElem
- (2)在顺序表的第i个位置插入新元素e,Listlnsert
- ①InsertElem(SeqList *list, int i, int e)函数解释
- ②为什么GetElem(SeqList list, int i)和InsertElem(SeqList *list, int i, int e)中的list不一样?
- (3)返回顺序表当前元素的个数
- (4)给定一个数e,查找顺序表中某个元素的值与e相同,返回其序号
- 六、顺序线性表的总结
- 优点:
- 缺点:
数据结构部分的知识框架

逻辑结构里面,线性表属于线性结构,是一个大类。区别与栈和队列、串等结构。

线性表主要从这8个部分进行学习。
一、线性表的定义和特点
1.定义
线性表是一种常见的数据结构,它是由一组有序的元素(节点)组成的数据序列。线性表中的元素之间存在一对一的关系,每个元素除了第一个元素外,都有唯一的前驱元素;每个元素除了最后一个元素外,都有唯一的后继元素。
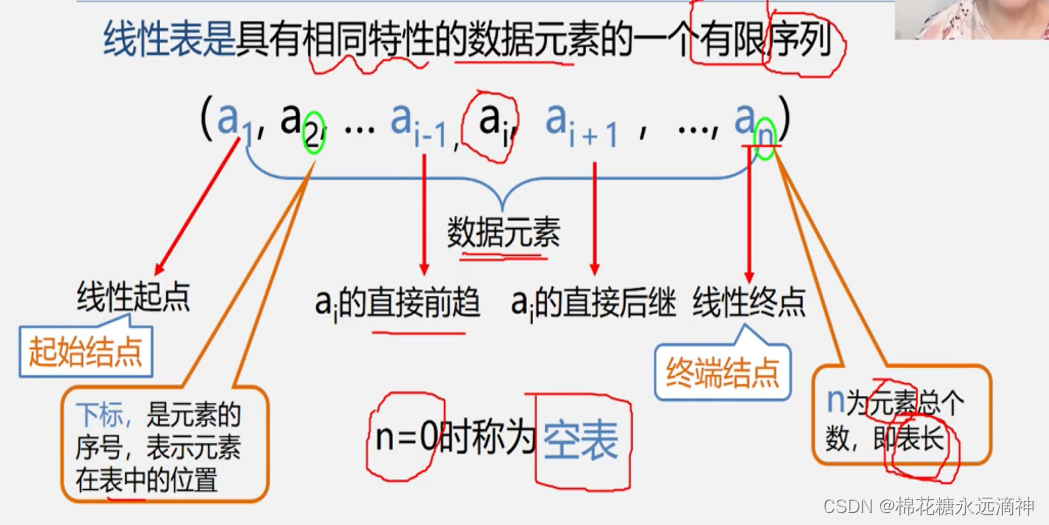
举一个例子:
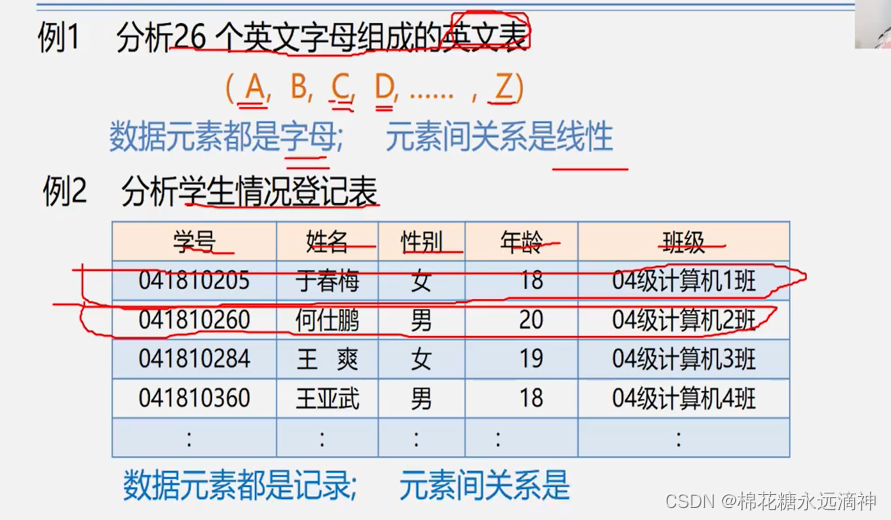
特点就是表里面的每个元素都具有相同的特征,要么都是字母,要么都是同一类的数据,而他们的关系就是一个接着一个连在一起。
2.特点
线性表的特点包括:
有序性:线性表中的元素按照一定的顺序排列,每个元素都有一个确定的位置。
唯一性:线性表中的元素都是唯一的,不存在相同的元素。
有限性:线性表中的元素个数是有限的,可以为空表(没有元素)或非空表(至少有一个元素)。

二、线性表的实际案例引入
1.案例一:多项式的加减乘除
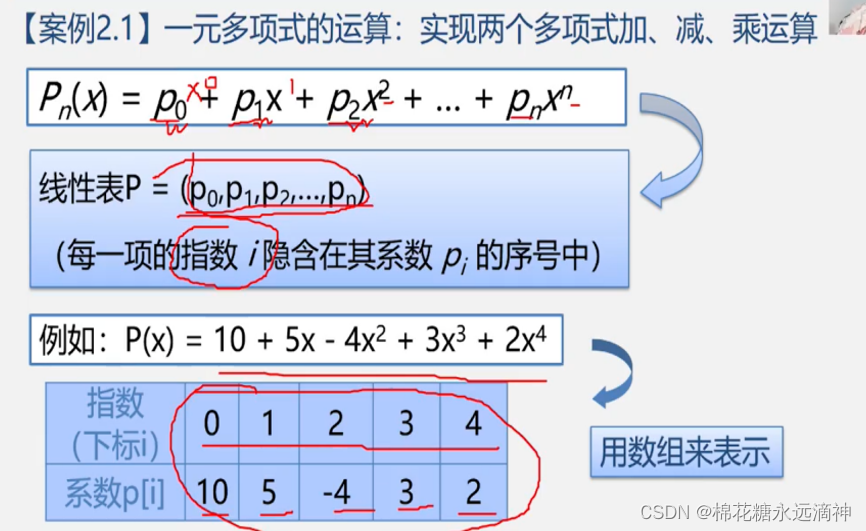
一个多项式的每一项的系数可以用一个一维数组来表示,那么我们要进行多个多项式的加减乘运算,就可以只对相同指数(意味着他们数组的下标相同)的系数相加就可以,比如i[1]+j[1]就是第一项的系数和。
2.案例二:当多项式是稀疏多项式时:
①稀疏多项式的定义:稀疏多项式(Sparse Polynomial)是指在多项式中,只有很少的系数是非零的情况下。具体地说,稀疏多项式是指多项式中的非零系数的数量远远小于总系数的数量。

如果是几个稀疏多项式的加减,不可能让那些系数为0的2、3、4、5、6、7次项都存入线性表,不能去建立一个20000个元素的线性表,造成存储空间浪费,那么应该怎么做呢?

以这个为例,把多项式每一项的系数和指数都存储起来,形成线性表A和B,
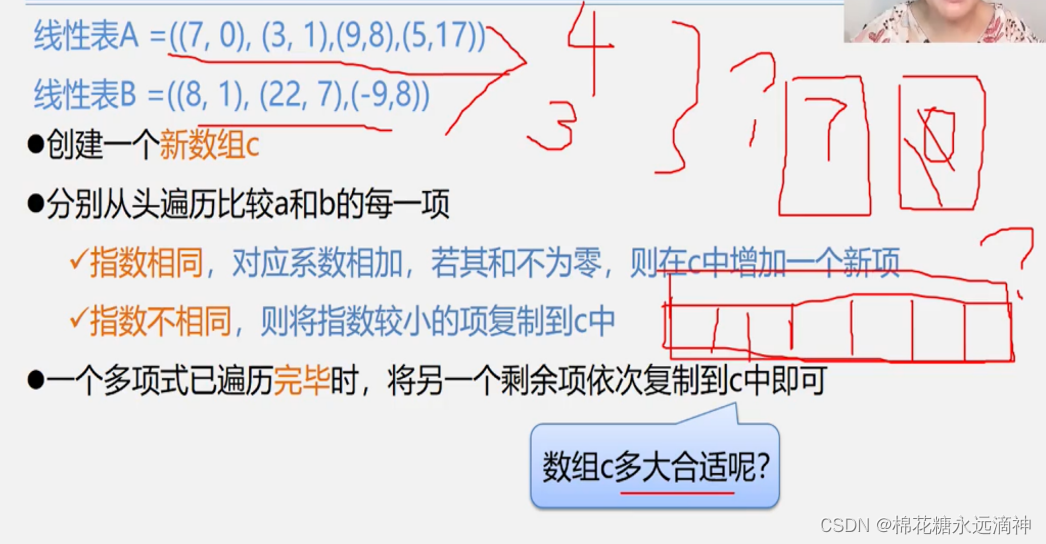
如图,创建新数组C,遍历线性表A和B,比较是否有指数相同或不相同项,然后把各个指数项复制到数组C中即可。以一个具体的C语言代码为例:
#include <stdio.h>
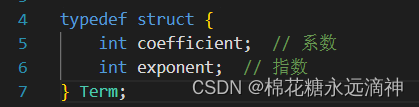
#include <stdlib.h>typedef struct {int coefficient; // 系数int exponent; // 指数
} Term;Term* addSparsePolynomials(Term* poly1, int size1, Term* poly2, int size2, int* resultSize) {int i = 0, j = 0, k = 0;int maxSize = size1 + size2;Term* result = (Term*)malloc(maxSize * sizeof(Term)); // 分配存储结果的数组while (i < size1 && j < size2) {if (poly1[i].exponent < poly2[j].exponent) {result[k++] = poly1[i++]; // 将poly1的项添加到结果中} else if (poly1[i].exponent > poly2[j].exponent) {result[k++] = poly2[j++]; // 将poly2的项添加到结果中} else {int coefficient = poly1[i].coefficient + poly2[j].coefficient; // 相同指数的项系数相加if (coefficient != 0) {result[k].coefficient = coefficient;result[k].exponent = poly1[i].exponent;k++;}i++;j++;}}while (i < size1) {result[k++] = poly1[i++]; // 将poly1剩余的项添加到结果中}while (j < size2) {result[k++] = poly2[j++]; // 将poly2剩余的项添加到结果中}*resultSize = k; // 更新结果的大小return result;
}// 示例用法
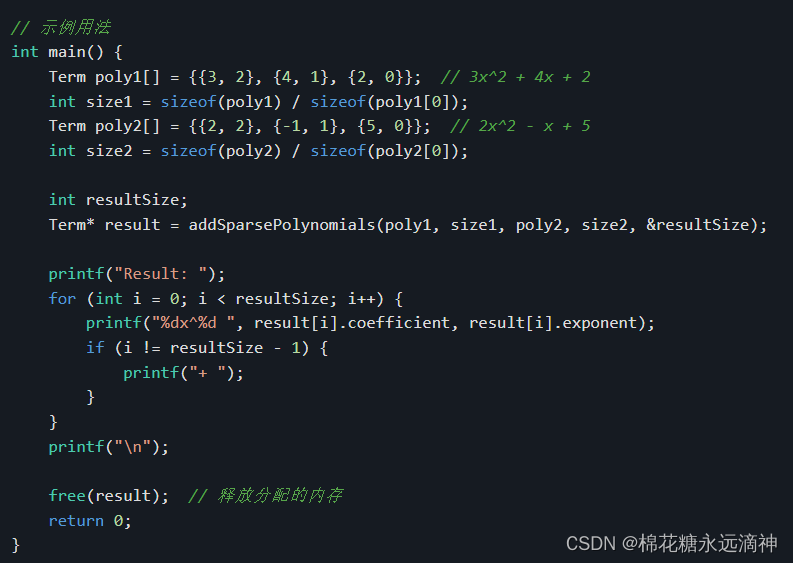
int main() {Term poly1[] = {{3, 2}, {4, 1}, {2, 0}}; // 3x^2 + 4x + 2int size1 = sizeof(poly1) / sizeof(poly1[0]);Term poly2[] = {{2, 2}, {-1, 1}, {5, 0}}; // 2x^2 - x + 5int size2 = sizeof(poly2) / sizeof(poly2[0]);int resultSize;Term* result = addSparsePolynomials(poly1, size1, poly2, size2, &resultSize);printf("Result: ");for (int i = 0; i < resultSize; i++) {printf("%dx^%d ", result[i].coefficient, result[i].exponent);if (i != resultSize - 1) {printf("+ ");}}printf("\n");free(result); // 释放分配的内存return 0;
}这段代码实现了稀疏多项式的相加功能。稀疏多项式是指只有部分项存在的多项式,其中存在很多指数为0的项,其他项的指数按递增顺序排列。
代码中首先定义了一个结构体Term,用于表示多项式的每一项。每一项包含两个成员变量,coefficient表示系数,exponent表示指数。
接下来是addSparsePolynomials函数,该函数接受两个多项式的数组poly1和poly2,以及它们的大小size1和size2。函数的目标是将这两个多项式相加,并返回结果的数组。
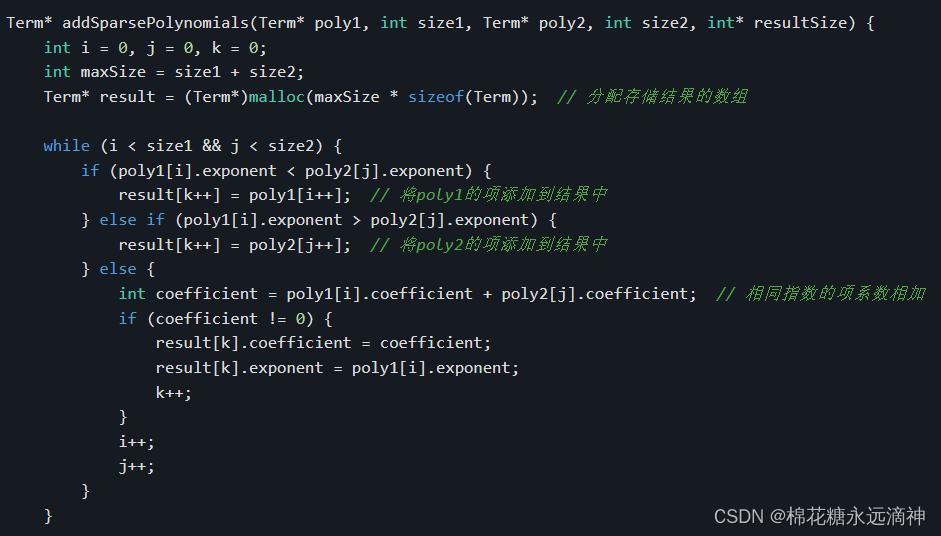
函数中使用了三个变量i、j和k来分别追踪poly1、poly2和result数组的索引。maxSize变量用于存储结果数组的最大大小,即两个输入多项式的大小之和。通过malloc函数动态分配了一个大小为maxSize的result数组。
接下来的while循环通过比较指数的大小来相加多项式。如果poly1的当前项的指数小于poly2的当前项的指数,则将poly1的当前项添加到结果数组中,并递增i和k。如果poly1的当前项的指数大于poly2的当前项的指数,则将poly2的当前项添加到结果数组中,并递增j和k。如果两个当前项的指数相等,则将它们的系数相加,如果系数不为0,则将结果项的系数和指数设置为相加后的值,并将结果项添加到结果数组中。然后递增i、j和k。

接下来的两个while循环用于将剩余的多项式项添加到结果数组中,即如果poly1还有剩余项,则将它们全部添加到结果数组中,递增i和k;如果poly2还有剩余项,则将它们全部添加到结果数组中,递增j和k。
最后,将结果的大小k存储到resultSize指针指向的变量中,并返回结果数组。
在main函数中,我们定义了两个多项式poly1和poly2,并计算它们的大小。然后调用addSparsePolynomials函数来求解它们的相加结果,并将结果存储在result数组中。最后,使用循环打印出结果数组中的项,并释放动态分配的内存。
3.案例三:图书管理系统
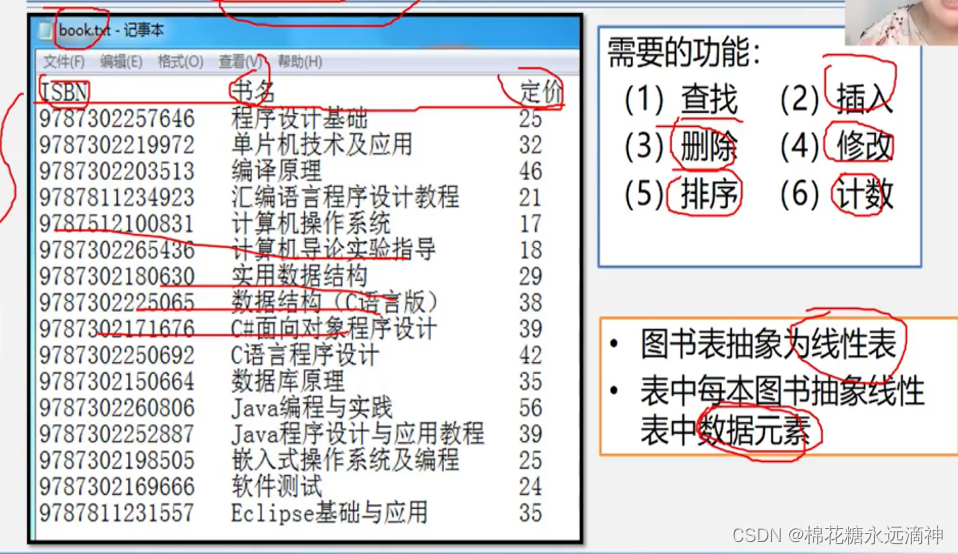
因为需要进行较多的查找、插入、删除、修改操作,使用链式结构的话会更加方便一些。链式结构只需要对节点进行修改,不像数组一样每次都要将插入节点之后所有的元素都整体后移或者前移,浪费时间,并且会频繁分配与释放内存。
三、线性表的类型定义
1.

这其中有很多伪代码组成的基本操作,这里不一一介绍了。
四、线性表的顺序表示和实现
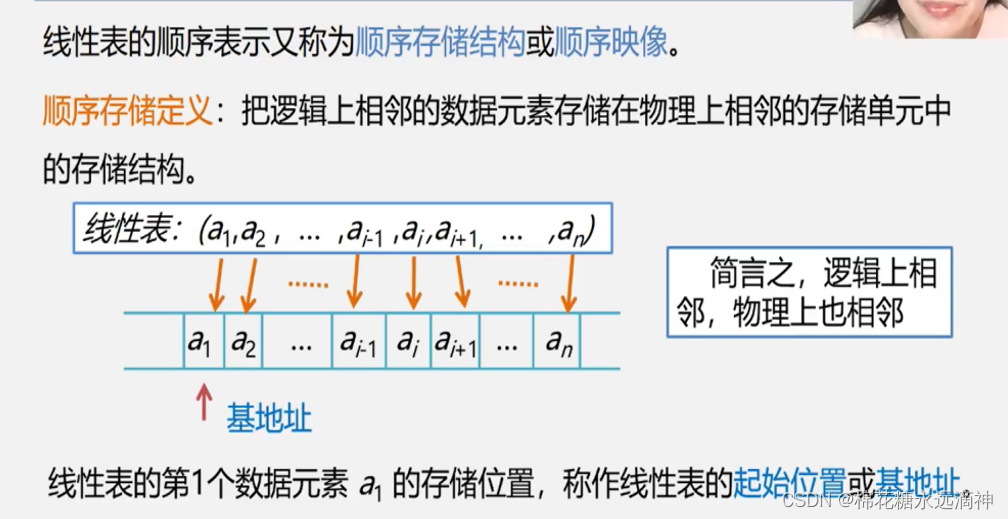
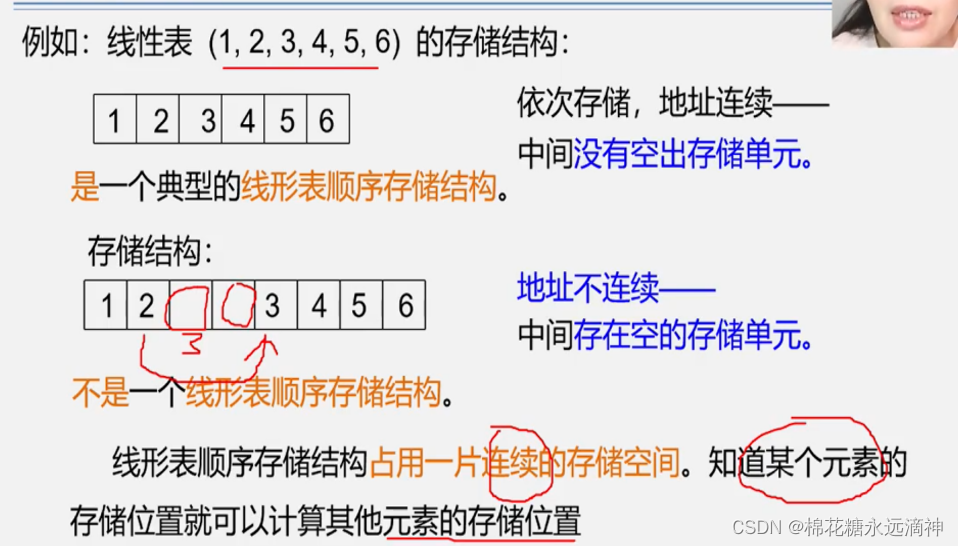
比如一个数组就是线性表,定义一个整形数组,一个元素占32位,即4个字节,已知第3个元素的位置的话,那么下一个元素位置就是指针指向+4个字节的位置。所以有个好处:查找表中的某一个元素非常方便。

这里有一个点:顺序线性表长度是可以变化的,但是初始建立顺序线性表时表的长度只能定义为一个准确的数值,而不是一个动态变化的变量。可以用这个模板作为线性表的构建:
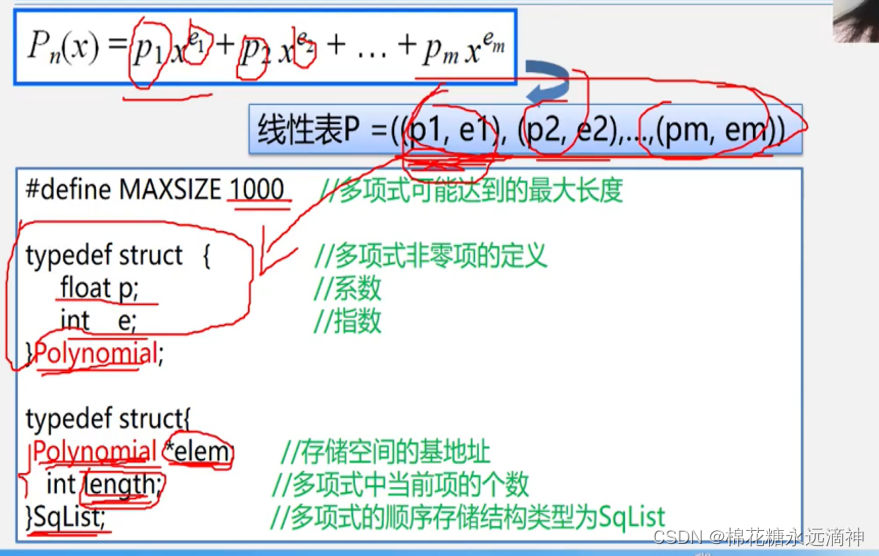
指针*elem指向结构体的起始地址。同时有一个嵌套结构体的结构体。
举一个实际的例子:
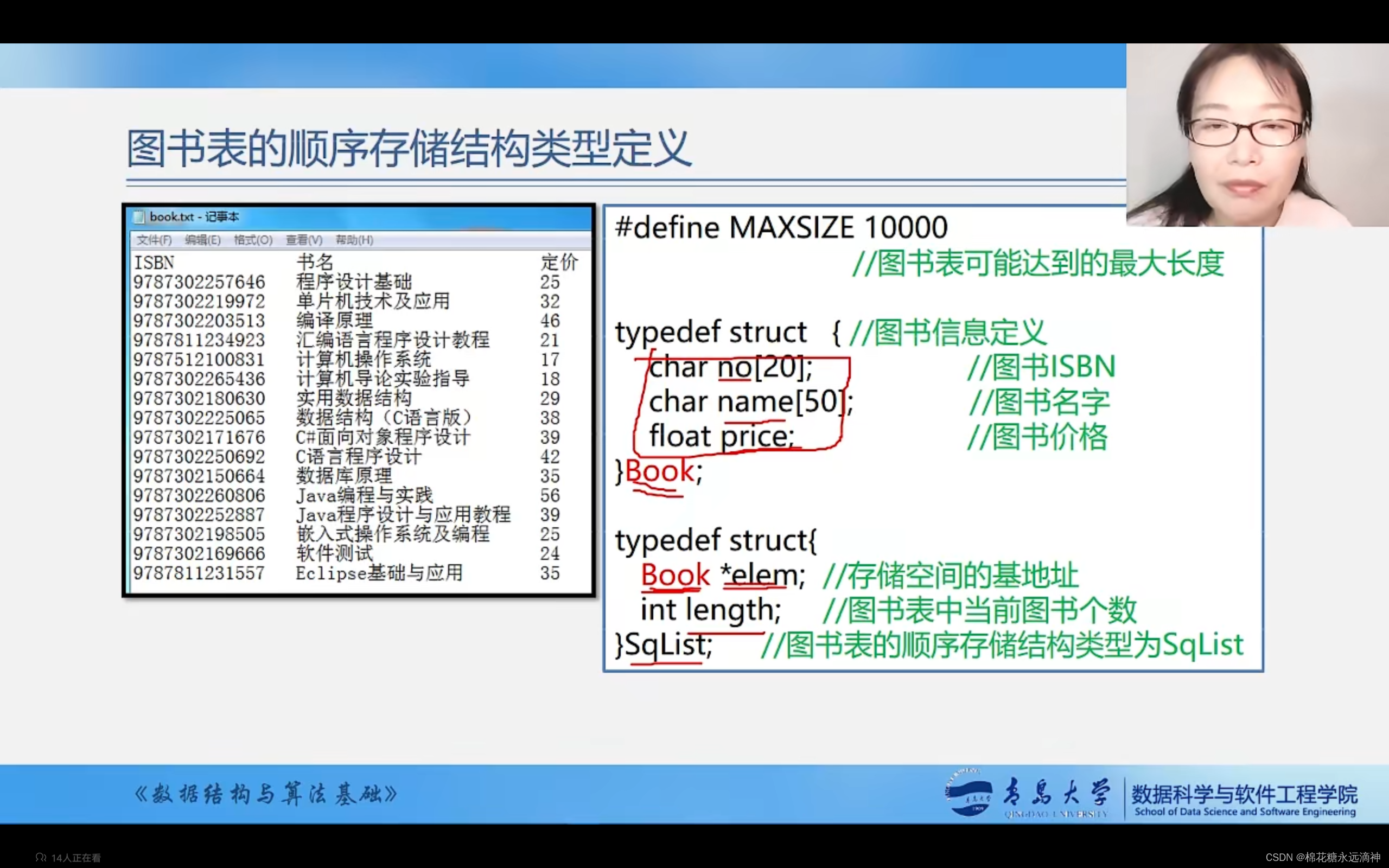
定义了一个线性表Book,成员包括ISBN码、名字和价格。又创建了一个结构体指针elem,length是线性表中的元素个数。
类C语言中的一些说明
1.结构体嵌套

这个结构体中的ElemType是什么类型的?
答:它是一个抽象类型,ElemType就是一个结构体的名字,
typedef struct {
int coefficient;
int exponent;
char name[20];
float price;
} ElemType;
ElemType内含多个数据类型,所以它是抽象的,可以定义成int型,也可以定义为char型。
2.静态数组与动态数组

静态数组中元素的大小是确定的,Maxsize是一个宏定义后的常量,但是动态数组的话,data可以通过函数如malloc()或new来进行,需要手动释放内存以避免内存泄漏。例如,int* arr = malloc(sizeof(int) * 10);。这样的话,sizeof()函数每次都可以计算变化后当前数组的大小,malloc()函数再开辟一块空间给数组。这几个函数有什么作用:
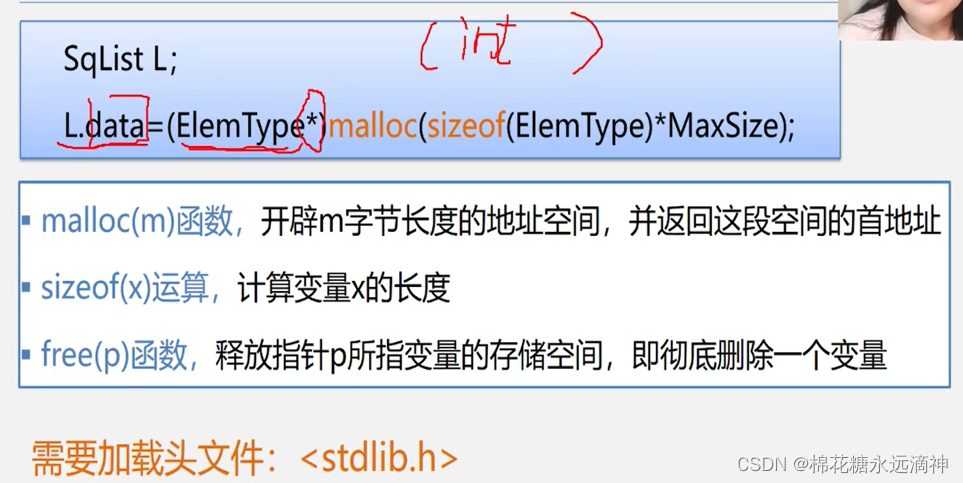
顺序表的示意图
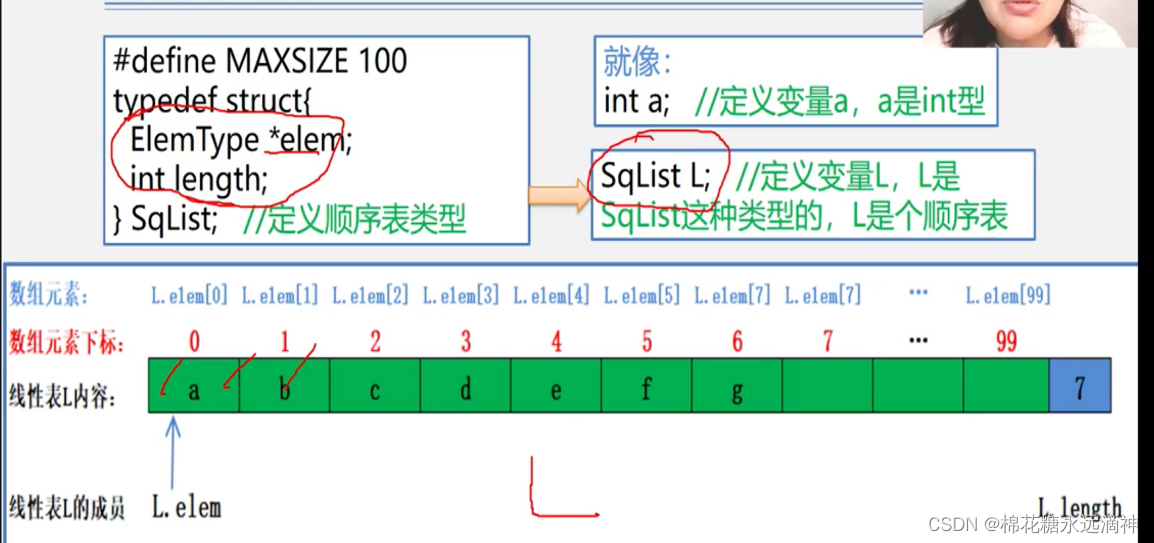
有了顺序表sqlist,还要定义一个变量L,L是顺序表类型。
如何操作线性表里面的元素呢?这一块的内容我下一节单独列出,写代码。

①线性表的插入元素

思考如何插入一个元素到线性表中:
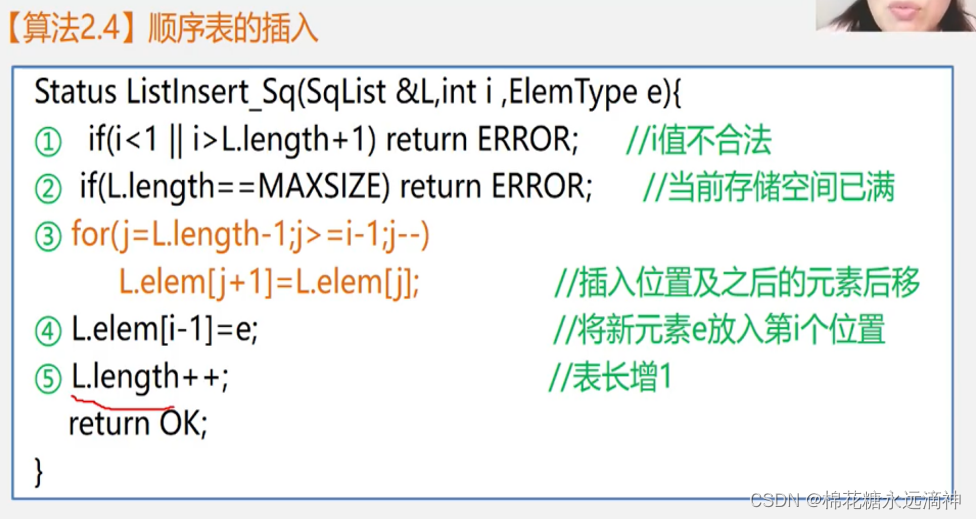
五、顺序表的元素操作代码表达
这里我主要写插入、删除元素、查找元素、返回顺序表元素个数、查找指定元素序号这5个操作。
我们知道C语言中数组的下标是从0开始的,要找到第n个元素,只需要访问下标n-1即可,对每个线性表位置的存入或者取出数据,对于计算机来说都是相等的时间 也就是个常数,因此用我们算法中学到的时间复杂度的概念来说,存取时间性能为 O(1),即为随机存取特性。根据这个特性就可以很方便的查找或者修改顺序表中某个指定位置的元素。
(1)查找(获得)第i个元素的值并返回该值GetElem
思路:检测i值是否在数组的下标范围内,如果在,就返回下标为i-1的元素
代码:
#include <stdio.h>
#include <stdlib.h>#define MAX_SIZE 100
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
typedef struct {int data[MAX_SIZE];//用于存储数据int length;//记录当前线性表的长度
} SeqList;int GetElem(SeqList list, int i) {if (i < 1 || i > list.length) {//一些不符合实际的情况return ERROR; // 返回一个无效值,表示查找失败}return list.data[i - 1];
}int main() {SeqList list;list.length = 5;list.data[0] = 10;list.data[1] = 20;list.data[2] = 30;list.data[3] = 40;list.data[4] = 50;int index = 3; // 要查找的元素的索引int result = GetElem(list, index);if (result != -1) {printf("The element at index %d is %d\n", index, result);}return 0;
}
核心很清楚,定义一个顺序表结构体,定义一个函数用来返回第i个元素的值,主程序初始化顺序表结构体变量,给表中元素添加值,然后获取并打印结果。
(2)在顺序表的第i个位置插入新元素e,Listlnsert
思路:
先检查这个i值的有效性,如果i值过小或者超出线性表范围,则返回错误。
从后往前遍历,将第i个位置后的所有元素均后移一位,就可以顺势把新元素插到i位置上了。
代码:
#include <stdio.h>#define MAX_SIZE 100typedef struct {int data[MAX_SIZE];int length;
} SeqList;int InsertElem(SeqList *list, int i, int e) {if (i < 1 || i > list->length + 1 || list->length == MAX_SIZE) {printf("Invalid position for insertion\n");return -1; // 返回一个无效值,表示插入失败}for (int j = list->length; j >= i; j--) {list->data[j] = list->data[j - 1];}list->data[i - 1] = e;list->length++;return 0; // 返回插入成功
}void PrintList(SeqList list) {for (int i = 0; i < list.length; i++) {printf("%d ", list.data[i]);}printf("\n");
}int main() {SeqList list;list.length = 5;list.data[0] = 10;list.data[1] = 20;list.data[2] = 30;list.data[3] = 40;list.data[4] = 50;int position = 3; // 要插入的位置int element = 25; // 要插入的元素if (InsertElem(&list, position, element) == 0) {printf("Insertion successful\n");PrintList(list);}return 0;
}解释:
①InsertElem(SeqList *list, int i, int e)函数解释
函数的实现逻辑如下:
首先,函数会检查插入位置的有效性。如果位置i小于1或大于顺序表的长度加1,或者顺序表已满,则插入位置无效,函数会打印一条错误消息并返回一个无效值(-1),表示插入失败。
如果插入位置有效,函数会将位置i及其之后的元素都向后移动一位,为新元素e腾出位置。这是通过一个循环来实现的,从顺序表的最后一个元素开始,依次将每个元素向后移动一位,直到位置i。
最后,函数将新元素e插入到位置i,并更新顺序表的长度。
②为什么GetElem(SeqList list, int i)和InsertElem(SeqList *list, int i, int e)中的list不一样?
在C语言中,参数传递有两种方式:值传递和指针传递。
值传递:当使用值传递方式传递参数时,函数会将参数的副本传递给函数,函数中对参数的修改不会影响到原始的参数。这意味着,如果函数需要对参数进行修改,那么修改的结果不会反映到函数外部。
指针传递:当使用指针传递方式传递参数时,函数会将参数的地址传递给函数,函数中对参数的修改会直接影响到原始的参数。这意味着,如果函数需要对参数进行修改,那么修改的结果会反映到函数外部。
在GetElem(SeqList list, int i)函数中,list以值传递方式传入。这是因为函数只需要读取顺序表中的元素,不需要对顺序表进行修改。
而在InsertElem(SeqList *list, int i, int e)函数中,list以指针传递方式传入。这是因为函数需要在顺序表中插入新元素,相当于对原始数据有了修改,所以需要对顺序表进行修改。
(3)返回顺序表当前元素的个数
代码:
int getCount(SeqList list) {return list.length;
}
不解释了
(4)给定一个数e,查找顺序表中某个元素的值与e相同,返回其序号
思路:遍历表,判断是否有相同的元素,如果是第i个元素与e相同,返回序号i-1.如果全部都没有,则返回error。
代码:
#include <stdio.h>#define MAX_SIZE 100typedef struct {int data[MAX_SIZE];int length;
} SeqList;int findElement(SeqList list, int e) {for (int i = 0; i < list.length; i++) {if (list.data[i] == e) {return i + 1; // 返回序号时需要加1,因为序号从1开始}}return -1; // 如果找不到,则返回-1表示未找到
}int main() {SeqList list;list.length = 5; // 假设顺序表中有5个元素list.data[0] = 10;list.data[1] = 20;list.data[2] = 30;list.data[3] = 40;list.data[4] = 50;int e = 30; // 假设要查找的元素为30int index = findElement(list, e);if (index == -1) {printf("未找到元素 %d\n", e);} else {printf("元素 %d 的序号为 %d\n", e, index);}return 0;
}六、顺序线性表的总结

线性表的顺序存储结构是使用数组来存储线性表的元素,具有以下优点和缺点:
优点:
随机访问:由于元素在数组中是连续存储的,可以通过下标直接访问任意位置的元素,具有快速的随机访问速度。
空间效率高:顺序存储结构只需要额外的一个数组来存储元素,不需要额外的指针等辅助空间,因此空间利用率高。
索引操作简单:通过下标索引即可访问和修改元素,操作简单明了。
缺点:
插入和删除操作耗时:在顺序存储结构中,插入和删除操作需要将插入或删除位置后面的元素依次后移或前移,需要移动大量元素,因此耗时较长。
动态扩容困难:顺序存储结构的数组大小是固定的,如果线性表的元素个数超过了数组的容量,需要重新分配更大的数组并将元素复制到新数组中,比较麻烦。
内存浪费:如果线性表的元素个数远小于数组的容量,会造成内存的浪费,因为数组的大小是固定的。
综上所述,顺序存储结构适合于需要频繁随机访问元素、对空间要求较高、不需要频繁插入和删除操作的场景。如果需要频繁的插入和删除操作,或者线性表的大小不确定,动态变化,就可以考虑使用其他存储结构,如链式存储结构(链表)来实现线性表。
相关文章:

数据结构与算法C语言版学习笔记(2)-线性表、顺序存储结构的线性表
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 数据结构部分的知识框架一、线性表的定义和特点1.定义2.特点 二、线性表的实际案例引入1.案例一:多项式的加减乘除2.案例二:当多项式是稀疏多…...
【vite】vite.defineConfig is not a function/npm无法安装第三方包问题
当使用vite命令 npm init vite-app 项目名称时配置 import vue from vitejs/plugin-vueexport default defineConfig({plugins: [vue()] })会报错vite.defineConfig is not a function 还有就是npm下载的时候也会报错 原因vite插件vitejs/plugin-vue和vite版本问题 解决 调…...

234. 回文链表 --力扣 --JAVA
题目 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 解题思路 判断链表是否为回文链表取决于链表中各个节点的值,所以可以通过存储各节点的值进行对比判断&…...
【JAVA学习笔记】65 - 文件类,IO流--节点流、处理流、对象流、转换流、打印流
项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter19/src/com/yinhai 文件 一、文件,流 文件,对我们并不陌生,文件是保存数据的地方,比如大家经常使用的word文档,txt文件,excel文件..都是文件。它既可以保存一张图片…...

R语言 复习 习题图片
这是日天土申哥不知道从哪淘来的R语言复习知识点图片,大部分内容都是课后习题的答案 加油吧,骚年,考个好分数...
c语言 结构体 简单实例
结构体 简单例子 要求: 结构体保存学生信息操作 代码 #include <stdio.h>//定义结构体 struct student{int ID;char name[20];char sex;char birthday[8];int grade; };int main(){int number;printf("请输入学生个数:");scanf(&quo…...

【ChatGPT】ChatGPT的自定义指令
ChatGPT的自定义指令 关于ChatGPT自定义指令的常见问题解答概述可用性如何使用您的数据自定义指令设置将应用于所有新聊天。启动新聊天可查看更改iOS & AndroidWeb 示例常见问题使用自定义指令的好处字符限制我的ChatGPT数据导出中是否包含自定义指令?当我删除我…...

《哥德尔、艾舍尔、巴赫——集异璧之大成》阅读笔记1
1、谁也不知道非智能行为和智能行为之间的界限在哪里。事实上,认为存在明显界限也许是愚蠢的。但是智能的基本能力还是确定的,它们是: 对于情境有很灵活的反应充分利用机遇弄懂含糊不清或彼此矛盾的信息认识到一个情境中什么是重要的因素&am…...

稳定细胞系构建技术介绍
抗体药物的开发是一个非常复杂的过程,构建适用于工业生产的高表达的稳定细胞株是抗体药工艺开发的起点和基础。一株稳定高产的工程细胞株不仅能显著增加单位体积产量,降低生产成本,还可以降低下游纯化工艺复杂度,确保获得安全&…...
k8s部署srs服务
k8s部署srs服务 项目需要把srs纳入k8s进行管理,需要通过k8s来部署srs服务然后原本的srs可以支持rtmp与webrtc两种,官网查了部署方式,k8s只有最基本的部署方式于是开始研究k8s部署能够正常推拉流的webrtc版本的srs 首先肯定是去官网查有无相关…...

使用Java分割PDF文件
在Java中,我们可以使用iText库来处理PDF文件。iText是一个流行的Java库,用于创建和处理PDF文件。在本篇博客中,我们将介绍如何使用Java分割一个PDF文件为多个小的PDF文件。 1. 引入iText依赖 首先,我们需要在项目中引入iText库的…...

LLM时代中的分布式AI
深度学习相较传统机器学习模型,对算力有更高的要求。尤其是随着深度学习的飞速发展,模型体量也不断增长。于是,前几年,我们看到了芯片行业的百家争鸣和性能指标的快速提升。正当大家觉得算力问题已经得到较大程度的缓解时…...
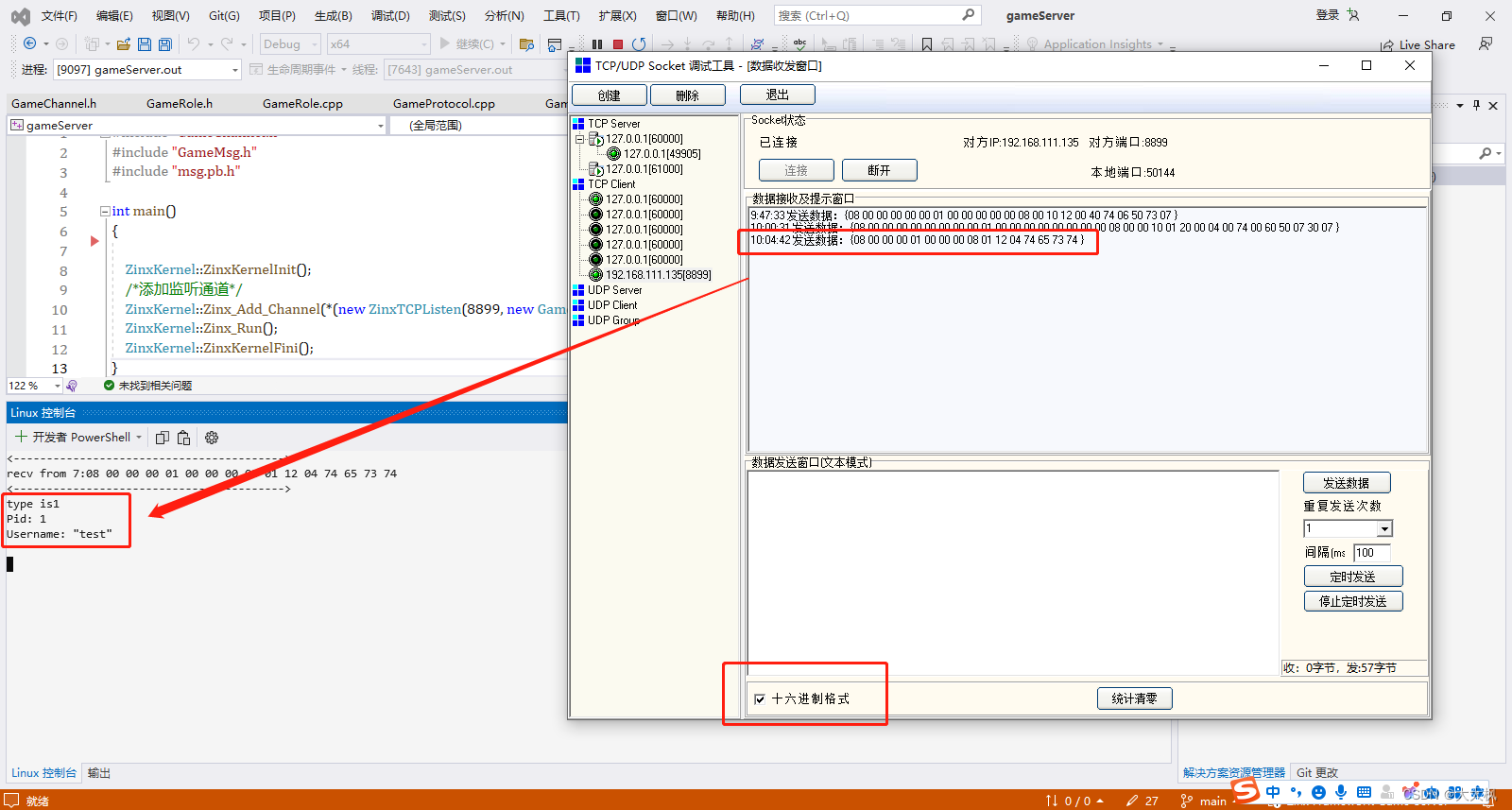
Zinx框架-游戏服务器开发003:架构搭建-需求分析及TCP通信方式的实现
文章目录 1 项目总体架构2 项目需求2.1 服务器职责2.2 消息的格式和定义 3 基于Tcp连接的通信方式3.1 通道层实现GameChannel类3.1.1 TcpChannel类3.1.2 Tcp工厂类3.1.3 创建主函数,添加Tcp的监听套接字3.1.4 代码测试 3.2 协议层与消息类3.2.1 消息的定义3.2.2 消息…...

如何使用Pyarmor保护你的Python脚本
目录 一、Pyarmor简介 二、使用Pyarmor保护Python脚本 1、安装Pyarmor 2、创建Pyarmor项目 3、添加Python脚本 4、配置执行环境 5、生成保护后的脚本 三、注意事项与未来发展 四、未来发展 五、总结 本文深入探讨了如何使用Pyarmor工具保护Python脚本。Pyarmor是一个…...

【c++】搜索二叉树的模拟实现
搜索二叉树的模拟实现 k模型完整代码 #pragma once namespace hqj1 {template<class K>struct SBTreeNode{public://这里直接用匿名对象作为缺省参数SBTreeNode(const K& key K()):_key(key), _cleft(nullptr), _cright(nullptr){}public:K _key;SBTreeNode* _cle…...
)
Kubeadm - K8S1.20 - 高可用集群部署(博客)
这里写目录标题 Kubeadm - K8S1.20 - 高可用集群部署一.环境准备1.系统设置 二.所有节点安装docker三.所有节点安装kubeadm,kubelet和kubectl1.定义kubernetes源2.高可用组件安装、配置 四.部署K8S集群五.问题解决1.加入集群的 Token 过期2.master节点 无法部署非系…...
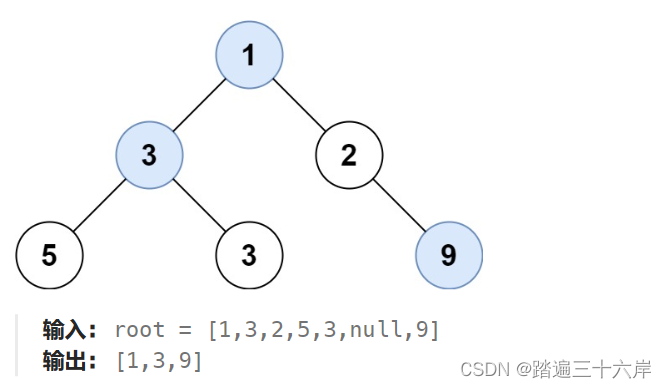
515. 在每个树行中找最大值
描述 : 给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。 题目 : LeetCode 在每个树行中找最大值 : 515. 在每个树行中找最大值 分析 : 这里其实就是在得到一层之后使用一个变量来记录当前得到的最大值 , 懂了前面的几道这就是小菜 解析 : /…...
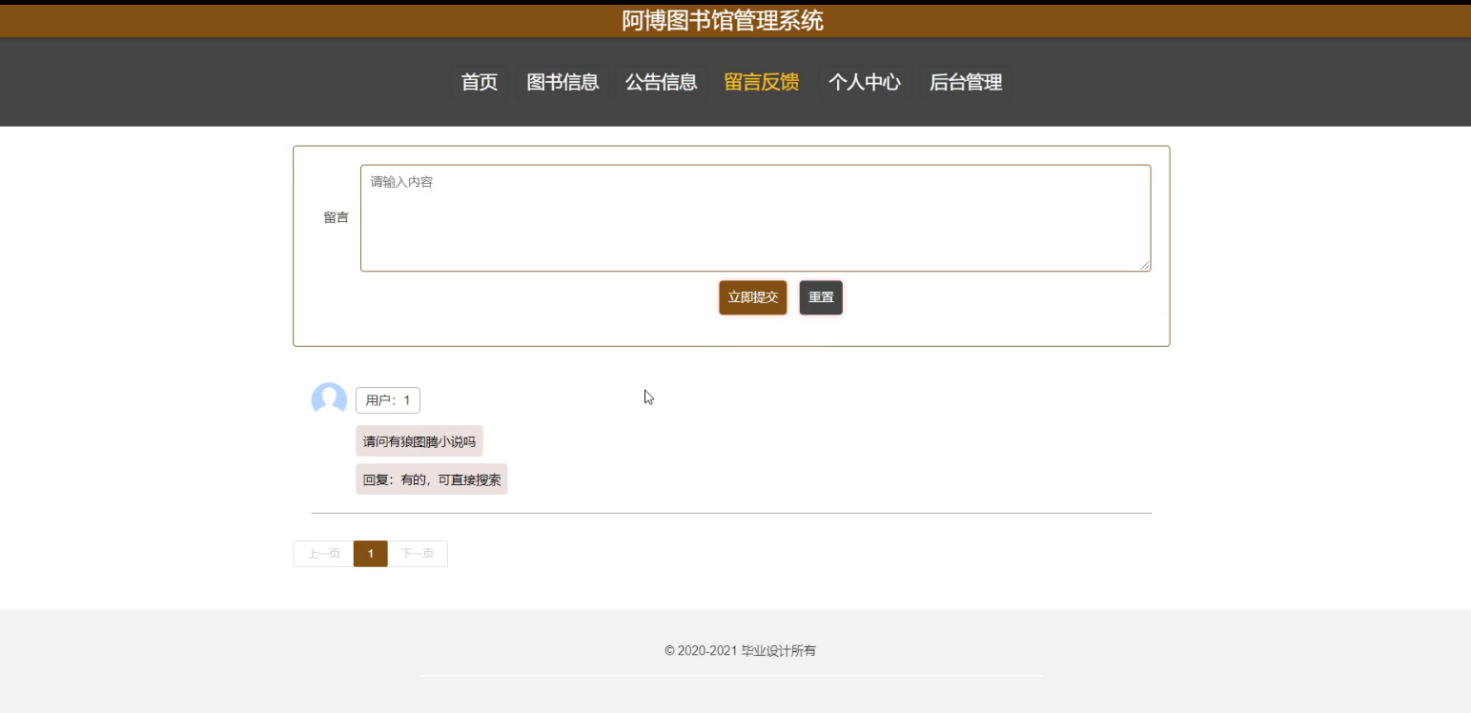
基于springboot+vue的图书馆管理系统
图书馆管理系统 springboot32阿博图书馆管理系统 源码合集: www.yuque.com/mick-hanyi/javaweb 源码下载:博主私 摘 要 随着社会的发展,计算机的优势和普及使得阿博图书馆管理系统的开发成为必需。阿博图书馆管理系统主要是借助计算机&…...

诊断刷写流程中使用到的诊断服务
10 01:诊断刷写完成后让目标ECU重置或让整车网络中其他ECU切换回默认会话 10 02:设置外部编程请求标志位或切换到编程会话(诊断刷写需要在编程会话下进行) 10 03:让目标ECU切换到扩展会话,以便进行其他诊断…...
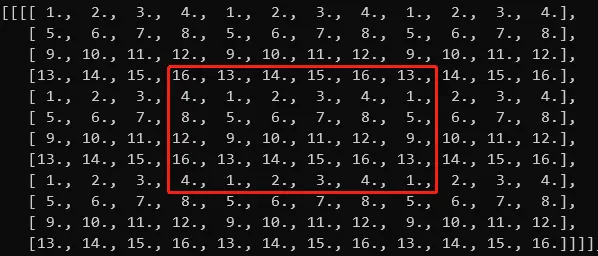
pytorch 中 nn.Conv2d 解释
1. pytorch nn.Con2d 中填充模式 torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue, padding_mode‘zeros’, deviceNone, dtypeNone) 1.1 padding 参数的含义 首先 ,padd N, 代表的是 分别在 上下&…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

GB/T 43887-2024 核级柔性石墨板材检测
核级柔性石墨板材是指以可膨胀石墨为原料、未经改性和增强、用于核工业的核级柔性石墨板材。 GB/T 43887-2024核级柔性石墨板材检测检测指标: 测试项目 测试标准 外观 GB/T 43887 尺寸偏差 GB/T 43887 化学成分 GB/T 43887 密度偏差 GB/T 43887 拉伸强度…...
)
python数据结构和算法(1)
数据结构和算法简介 数据结构:存储和组织数据的方式,决定了数据的存储方式和访问方式。 算法:解决问题的思维、步骤和方法。 程序 数据结构 算法 算法 算法的独立性 算法是独立存在的一种解决问题的方法和思想,对于算法而言&a…...
