[蓝桥杯 2022 省 A] 推导部分和
[蓝桥杯 2022 省 A] 推导部分和
题目描述
对于一个长度为 N N N 的整数数列 A 1 , A 2 , ⋯ A N A_{1}, A_{2}, \cdots A_{N} A1,A2,⋯AN,小蓝想知道下标 l l l 到 r r r 的部分和 ∑ i = l r A i = A l + A l + 1 + ⋯ + A r \sum\limits_{i=l}^{r}A_i=A_{l}+A_{l+1}+\cdots+A_{r} i=l∑rAi=Al+Al+1+⋯+Ar 是多少?
然而,小蓝并不知道数列中每个数的值是多少,他只知道它的 M M M 个部分和的值。其中第 i i i 个部分和是下标 l i l_{i} li 到 r i r_{i} ri 的部分和 ∑ j = l i r i = A l i + A l i + 1 + ⋯ + A r i \sum_{j=l_{i}}^{r_{i}}=A_{l_{i}}+A_{l_{i}+1}+\cdots+A_{r_{i}} ∑j=liri=Ali+Ali+1+⋯+Ari, 值是 S i S_{i} Si 。
输入格式
第一行包含 3 个整数 N 、 M N 、 M N、M 和 Q Q Q。分别代表数组长度、已知的部分和数量 和询问的部分和数量。
接下来 M M M 行,每行包含 3 3 3 个整数 l i , r i , S i l_{i}, r_{i}, S_{i} li,ri,Si。
接下来 Q Q Q 行,每行包含 2 2 2 个整数 l l l 和 r r r,代表一个小蓝想知道的部分和。
输出格式
对于每个询问, 输出一行包含一个整数表示答案。如果答案无法确定, 输出 UNKNOWN。
样例 #1
样例输入 #1
5 3 3
1 5 15
4 5 9
2 3 5
1 5
1 3
1 2
样例输出 #1
15
6
UNKNOWN
提示
对于 10 % 10 \% 10% 的评测用例, 1 ≤ N , M , Q ≤ 10 , − 100 ≤ S i ≤ 100 1 \leq N, M, Q \leq 10,-100 \leq S_{i} \leq 100 1≤N,M,Q≤10,−100≤Si≤100 。
对于 20 % 20 \% 20% 的评测用例, 1 ≤ N , M , Q ≤ 20 , − 1000 ≤ S i ≤ 1000 1 \leq N, M, Q \leq 20,-1000 \leq S_{i} \leq 1000 1≤N,M,Q≤20,−1000≤Si≤1000 。
对于 30 % 30 \% 30% 的评测用例, 1 ≤ N , M , Q ≤ 50 , − 10000 ≤ S i ≤ 10000 1 \leq N, M, Q \leq 50,-10000 \leq S_{i} \leq 10000 1≤N,M,Q≤50,−10000≤Si≤10000 。
对于 40 % 40 \% 40% 的评测用例, 1 ≤ N , M , Q ≤ 1000 , − 1 0 6 ≤ S i ≤ 1 0 6 1 \leq N, M, Q \leq 1000,-10^{6} \leq S_{i} \leq 10^{6} 1≤N,M,Q≤1000,−106≤Si≤106 。
对于 60 % 60 \% 60% 的评测用例, 1 ≤ N , M , Q ≤ 10000 , − 1 0 9 ≤ S i ≤ 1 0 9 1 \leq N, M, Q \leq 10000,-10^{9} \leq S_{i} \leq 10^{9} 1≤N,M,Q≤10000,−109≤Si≤109 。
对于所有评测用例, 1 ≤ N , M , Q ≤ 1 0 5 , − 1 0 12 ≤ S i ≤ 1 0 12 , 1 ≤ l i ≤ r i ≤ N 1 \leq N, M, Q \leq 10^{5},-10^{12} \leq S_{i} \leq 10^{12}, 1 \leq l_{i} \leq r_{i} \leq N 1≤N,M,Q≤105,−1012≤Si≤1012,1≤li≤ri≤N, 1 ≤ l ≤ r ≤ N 1 \leq l \leq r \leq N 1≤l≤r≤N 。数据保证没有矛盾。
蓝桥杯 2022 省赛 A 组 J 题。
分析:
居然是一道图论建模题。。
对于一个部分和的关系,利用前缀和的思想,我们可以理解为是:
s [ r ] − s [ l − 1 ] = v s[r]-s[l-1]=v s[r]−s[l−1]=v
其实类比差分约束的思想就是让 l − 1 l-1 l−1到 r r r之间连一条长度为v的边
( l − 1 , r , v ) , ( r , l − 1 , − v ) (l-1,r,v),(r,l-1,-v) (l−1,r,v),(r,l−1,−v)
建完边之后各个部分和之间的关系也就一目了然了
接下来我们只需要利用 D F S DFS DFS或者 B F S BFS BFS遍历这张图,用并查集将具有相同标准的前缀和放在一个块里(一个快里面的任何数都可以作为标准),在一个块里的任何两个数我们都能知道他们之间的部分和
Code
#include<bits/stdc++.h>
using namespace std;#define int long longconst int N = 2e5+100;
int n,m,q;
int Hom[N],cnt = 0;
bool vi[N];
struct Node{int y,Next,v;
}e[2*N];
int Linkk[N] , len;
int s[N];
int fa[N];void Insert(int x,int y,int v){e[++len] = (Node){y,Linkk[x],v};Linkk[x] = len;
}int Getfa(int x){return fa[x] == x?x:fa[x] = Getfa(fa[x]);
}void Dfs(int x,int vv){vi[x] = 1;s[x] = vv;for (int i = Linkk[x]; i; i = e[i].Next){int y = e[i].y;if (vi[y]) continue;fa[Getfa(y)] = Getfa(x);Dfs(y,vv+e[i].v);}
}signed main(){scanf("%lld %lld %lld",&n,&m,&q);for (int i = 1,x,y,v; i <= m; i++)cin>>x>>y>>v,Insert(x-1,y,v),Insert(y,x-1,-v);for (int i = 0; i <= n; i++) fa[i] = i;for (int i = 0; i <= n; i++)if (!vi[i]) Dfs(i,0);for (int i = 1; i <= q; i++){int l,r;cin>>l>>r;if (Getfa(l-1)!=Getfa(r)) {cout<<"UNKNOWN"<<endl;continue;}printf("%lld\n",s[r]-s[l-1]);}return 0;
}
相关文章:

[蓝桥杯 2022 省 A] 推导部分和
[蓝桥杯 2022 省 A] 推导部分和 题目描述 对于一个长度为 N N N 的整数数列 A 1 , A 2 , ⋯ A N A_{1}, A_{2}, \cdots A_{N} A1,A2,⋯AN,小蓝想知道下标 l l l 到 r r r 的部分和 ∑ i l r A i A l A l 1 ⋯ A r \sum\limits_{il}^{r}A_iA_{l}A…...
pytorch复现_UNet
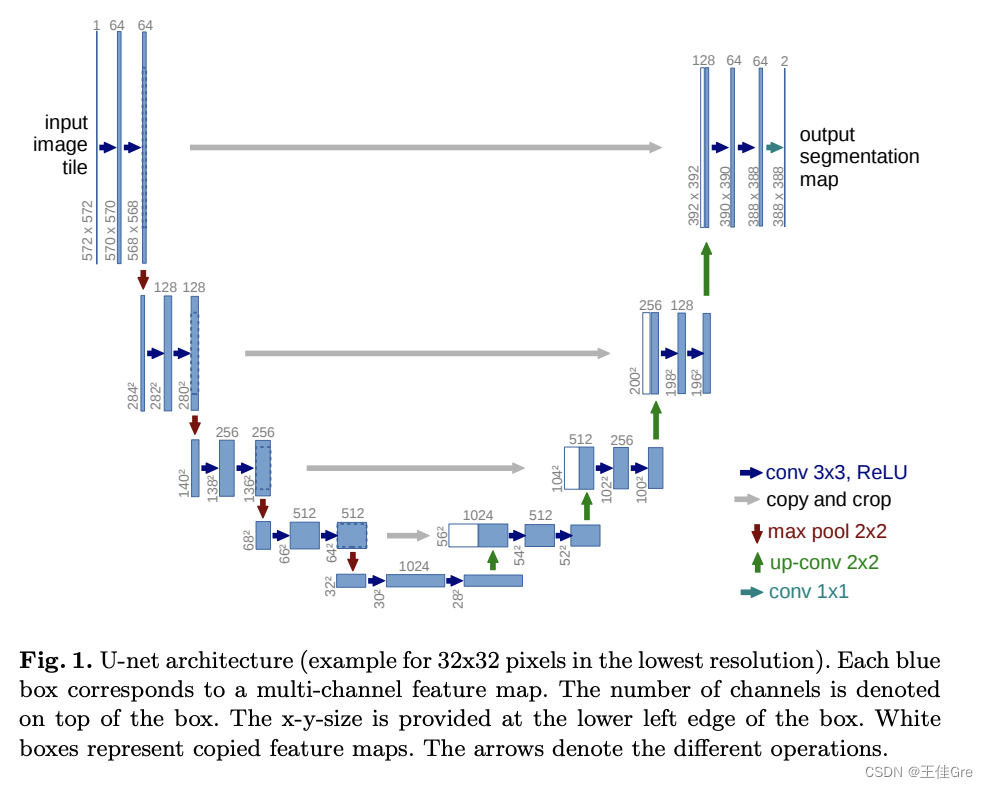
什么是UNet U-Net由收缩路径和扩张路径组成。收缩路径是一系列卷积层和汇集层,其中要素地图的分辨率逐渐降低。扩展路径是一系列上采样层和卷积层,其中特征地图的分辨率逐渐增加。 在扩展路径中的每一步,来自收缩路径的对应特征地图与当前特征…...
定岗定编设计:企业职能部门定岗定编设计项目成功案例
一、客户背景及现状分析 某大型车辆公司隶属于某央企集团,建于20世纪60年代,是中国高速、重载、专用铁路车辆生产经营的优势企业,轨道车辆制动机研发制造的主导企业,是隶属于国内最大的轨道交通设备制造上市企业的骨干二级公司。公…...
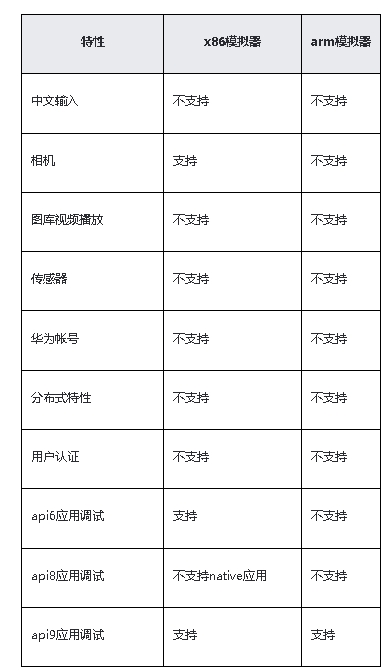
鸿蒙原生应用开发-DevEco Studio本地模拟器的使用
使用Local Emulator运行应用/服务 DevEco Studio提供的Local Emulator可以运行和调试Phone、TV和Wearable设备的HarmonyOS应用/服务。在Local Emulator上运行应用/服务兼容签名与不签名两种类型的HAP。 Local Emulator相比于Remote Emulator的区别:Local Emulator是…...

QT blockingFilter blockingMap blockingMapped
blockingFilter 主要作用是筛选出符合条件的项值结果集,并与之替换原有序列列表 blockingMap 可以直接修改容器的每一项 blockingMapped 不直接修改容器的每一项,而是将处理后的结果返回一个新的容器 blockingMappedReduced ResultType QtConcurrent::blockingMappedRed…...

【ARFoundation学习笔记】平面检测
写在前面的话 本系列笔记旨在记录作者在学习Unity中的AR开发过程中需要记录的问题和知识点。难免出现纰漏,更多详细内容请阅读原文。 文章目录 平面检测属性可视化平面平面检测的开关控制显示与隐藏已检测平面 平面检测属性 AR中检测平面的原理:AR Fou…...
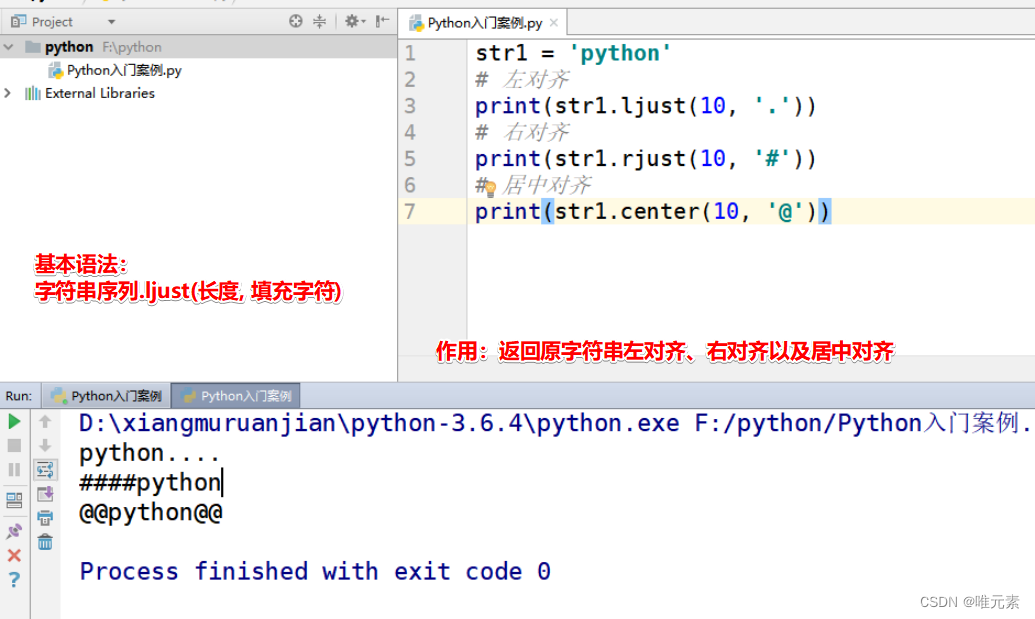
Python---ljust()--左对齐、rjust()--右对齐、center()--居中对齐
作用:返回原字符串左对齐、右对齐以及居中对齐,不足的使用 指定字符 进行填充。 ljust 左对齐 rjust 右对齐 center 居中对齐 类似于Excel、Word文档中的对齐。 基本语法: 字符串序列.ljust(长度, 填充字符) 案例: …...
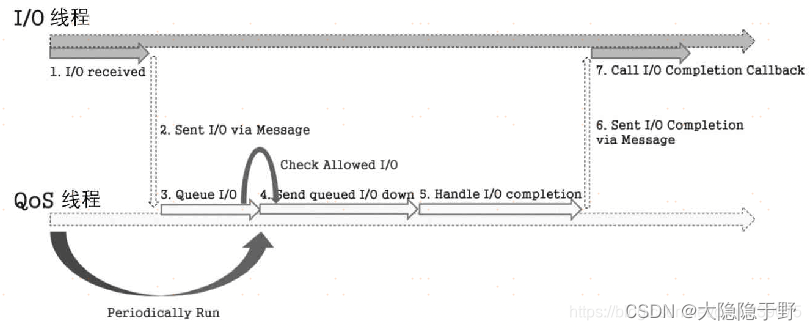
spdk用户态块层详解
先通过回顾内核态的通用块层来详细介绍SPDK通用块层,包括通用块层的架构、核心数据结构、数据流方面的考量等。最后描述基于通用块层之上的两个特性:一是逻辑卷的支持,基于通用块设备的Blobstore和各种逻辑卷的特性,精简配置&…...
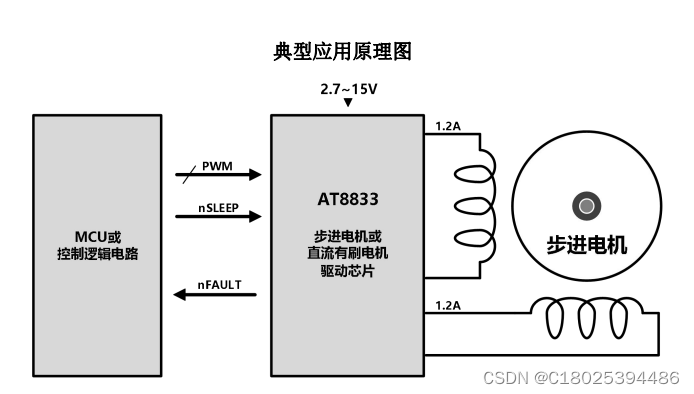
双通道 H 桥电机驱动芯片AT8833,软硬件兼容替代DRV8833,应用玩具、打印机等应用
上期小编给大家分享了单通道 H 桥电机驱动芯片,现在来讲一讲双通道的驱动芯片。 双通道 H 桥电机驱动芯片能通过控制电机的正反转、速度和停止等功能,实现对电机的精确控制。下面介绍双通道H桥电机驱动芯片的工作原理和特点。 一、工作原理 双通道 H 桥电…...
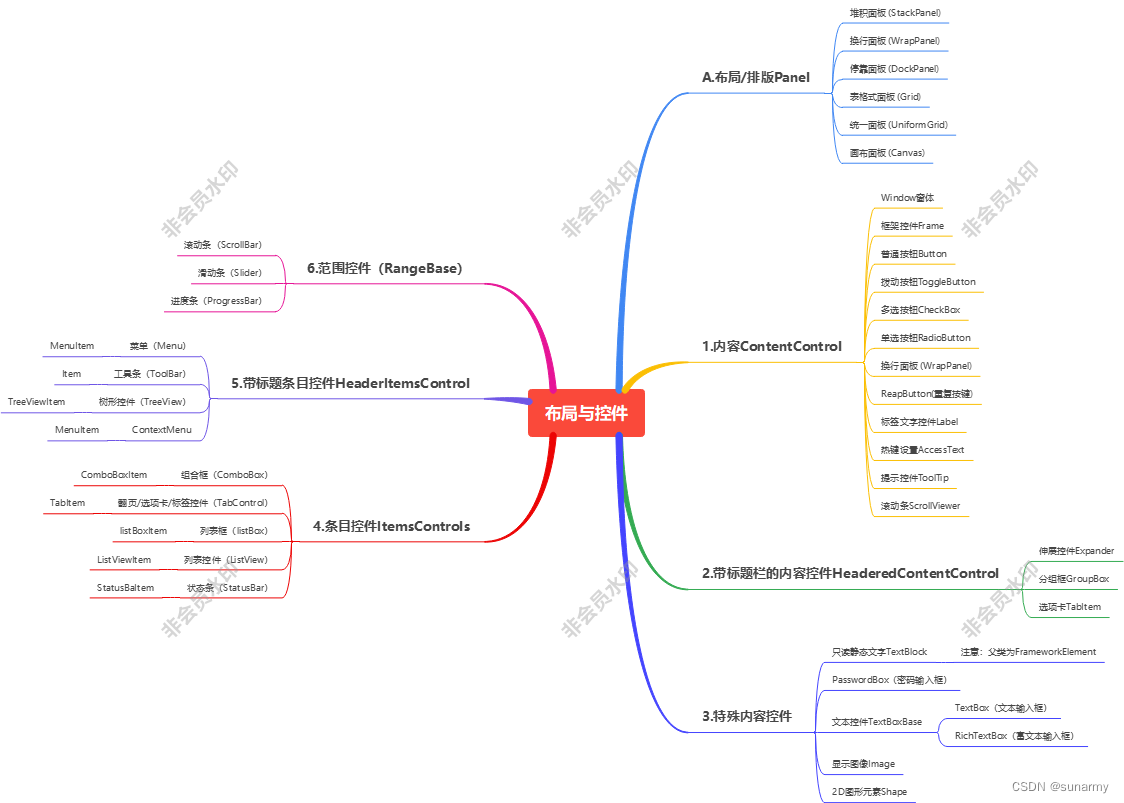
WPF布局与控件分类
Refer:WPF从假入门到真的入门 - 知乎 (zhihu.com) Refer:WPF从假入门到真的入门 - 知乎 (zhihu.com) https://www.zhihu.com/column/c_1397867519101755392 https://blog.csdn.net/qq_44034384/article/details/106154954 https://www.cnblogs.com/mq0…...
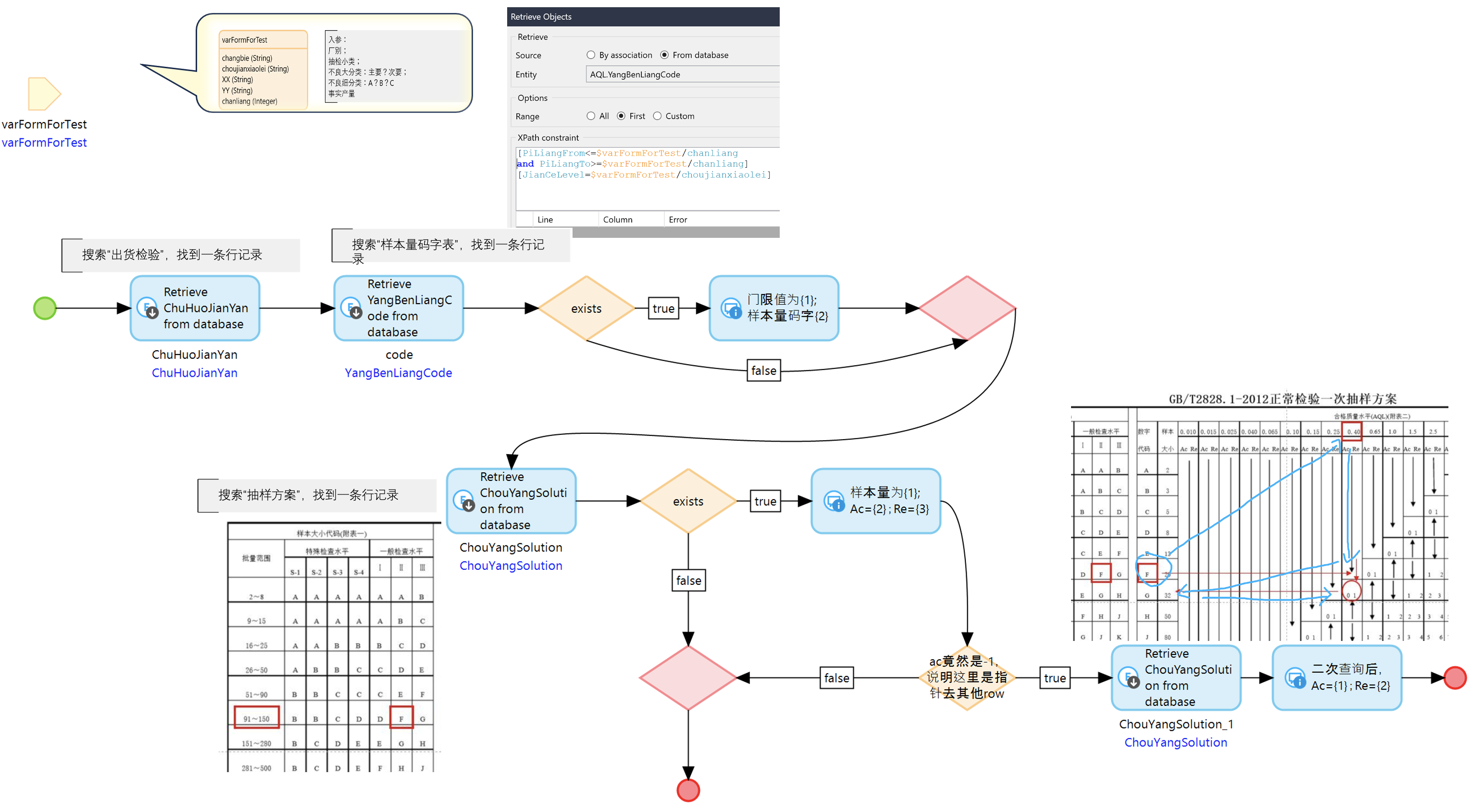
复杂逻辑的开发利器—Mendix快速实现AQL质量抽检
Mendix低代码开发平台适用于复杂的业务逻辑场景,这句话大家早有耳闻,本期小编就为您打开智慧之光,仅从AQL小侧面,来管窥一二——Mendix如何形成第五代编程语言,来完成数据逻辑与建模、业务算法逻辑与建模的。ÿ…...
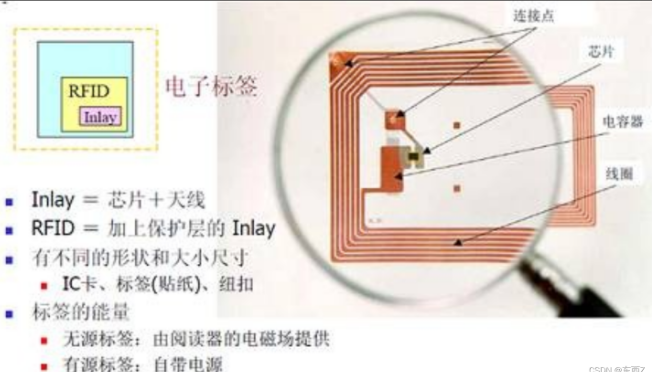
RFID系统
目录 在物联网应用中有三项关键技术 读写器 电子标签 工作原理 阅读器的组成及作用: 电子标签的组成及作用: RFID系统的组成 接口方式 在物联网应用中有三项关键技术 在物联网应用中有三项关键技术 1、传感器技术:这也是计算机应用中…...

Markov Chain Fingerprinting to Classify Encrypted Traffic 论文笔记
0.Abstract 在本文中,提出了用于SSL/TLS会话中传输的应用程序流量的随机指纹。这个指纹基于一阶齐次马尔可夫链,模型识别应用程序的准确率,并提供了检测异常对话的可能性。 1.Introduction 通过SSL/TLS会话时的头部信息创建统计指纹ÿ…...
)
vue 跨标签页的数据共享(即跨标签页通信)
跨标签页通信的常见方案 LocalStorage 或 SessionStorage BroadCast Channel Service Worker Shared Worker Window.postMessage() Cookies IndexedDB 什么是跨标签页通信? 指在同一个浏览器窗口中的多个标签页之间进行数据交流和信息传递的过程。通常情况…...

什么是拉宾-斯科特定理?
拉宾-斯科特定理(Rabin-Scott theorem )是数学上最深刻的数学结果之一。拉宾-斯科特定理是人们最喜欢的计算机科学概念之一。 当正确理解拉宾-斯科特定理时,它会以一种相当基本的方式改变你对现实的看法。然而,它典型的教科书式的呈现方式掩盖了这种深…...
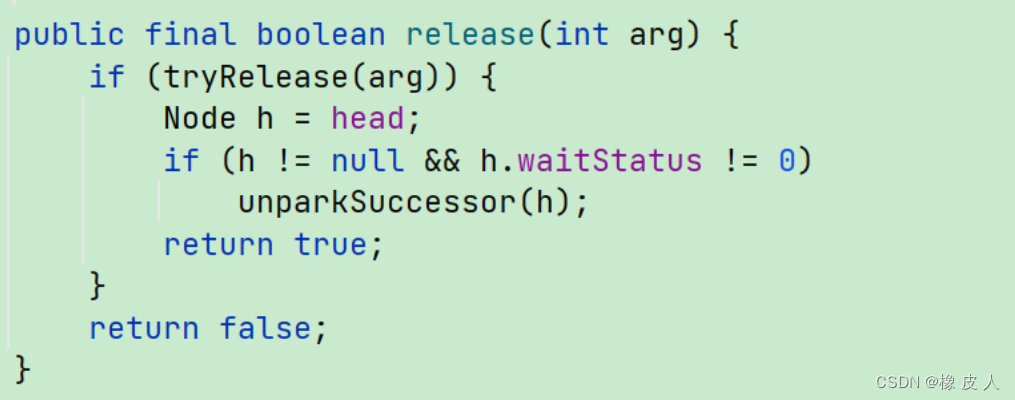
Java并发编程第11讲——AQS设计思想及核心源码分析
Java并发包(JUC)中提供了很多并发工具,比如前面介绍过的ReentrantLock、ReentrantReadWriteLock、CountDownLatch、Semaphore、FutureTask等锁或者同步部件,它们的实现都用到了一个共同的基类——AbstractQueuedSynchronizer&…...

什么是数据库?数据库有哪些基本分类和主要特点?
数据库是以某种有组织的方式存储的数据集合。本文从数据库的基本概念出发,详细解读了数据库的主要类别和基本特点,并就大模型时代备受瞩目的数据库类型——向量数据库进行了深度剖析,供大家在了解数据库领域的基本概念时起到一点参考作用。 …...

flutter显示出底部控件的引导页
需求:同一个页面的两个不同的入口,同一个控件的位置有变化,显示引导页时对应这个控件的引导内容的位置也需要改变;同时半透明底部显示出真实的页面内容。 这样的需要如果切图然后再往页面上贴位置无法精确的对准。 思路࿱…...

常用设计模式——模板方法模式
什么是模板方法模式 模板方法模式:定义一个操作中的算法的骨架,而将一些步骤延迟到子类中。模板方法使得子类可以不改变一个算法的结构即可重定义该算法的某些特定步骤。 主要解决:一些方法通用,却要在每一个子类都重写这些方法…...
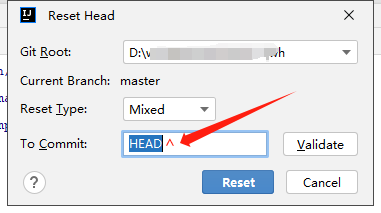
idea使用git删除本地提交(未推送)
1、找到reset head 2、打开弹窗,在HEAD后面输入^ 结果为HEAD^ 注释: Reset Type 有三种: Mixed(默认方式),保留本地源码,回退 commit 和 index 信息,最常用的方式Soft 回退到某个版本…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
