什么是拉宾-斯科特定理?
拉宾-斯科特定理(Rabin-Scott theorem )是数学上最深刻的数学结果之一。拉宾-斯科特定理是人们最喜欢的计算机科学概念之一。
当正确理解拉宾-斯科特定理时,它会以一种相当基本的方式改变你对现实的看法。然而,它典型的教科书式的呈现方式掩盖了这种深度。
假设有两台计算机:
- 有一台非确定性计算机(从形式逻辑上来说,是一个非确定性有限自动机,注意是非确定性的),它可以从给定的输入状态执行一整棵可能的操作树。(提供了多种可能性路径,但没有一条是确定的路径)
- 另外有一台确定性计算机,它只能遵循一条确定路径。
好像第一台计算机更好,对吗?(表面上,第一台计算机提供的路径数量多,其实没有p用,都是不确定的)
不。拉宾-斯科特定理说,第2台计算机虽然只有一条确定性路径,但可以通过将计算的每个状态定义为第一台可能状态的“集合”来模拟第一台的状态。
所以第二台计算的状态空间就是第一台的幂集(即可能子集的集合)。
因此,第二台的状态空间比第一台的状态空间指数大(大小为 2^n),复杂了,但核心要点仍然成立:第一台可以计算的所有内容,第二台也可以计算。
好吧,这很酷,但这里可以挖掘出有关(非)决定论本质的更深刻的教训:
大多数人都熟悉这样的想法:如果你有某个东西的确定性模型,你也可能会通过删除一些信息或对某些自由度进行粗粒度化来使其反而变得不确定了。
但熟悉相反情况的人却少得多。
也就是说,如果您有某个事物的不确定性模型,您始终可以创建一个等效的确定性模型(产生相同的预测),其状态空间只是原始模型的幂集。
这一事实在科学哲学中(很大程度上)被忽视了。
结论
确定性和非确定性不是*系统*的属性,而是*模型*的属性。
因此,如果提出这样的问题:“宇宙是确定性的吗?”根本没有意义。或“量子力学是非确定性的吗?”甚至“人类有自由意志吗?”都是没有意义。
有时确定性地对这些事物进行建模很有用,有时则不然。但永远不要忘记,决定论和非决定论的这些概念是*我们*通过选择模型引入的人类概念。从根本上来说,宇宙并不关心(banq注:因为是人类制造的词语陷阱、语言游戏、词语上下文)。
banq注:这是关于判别问题本身好不好的:如果一个问题有很多可能的不确定的解答,还不如有一个有确定性解答。
如果有人问你:人生意义是什么?理想社会是什么 ?宇宙是确定的吗? 人类有自由意志吗? 这些问题都没有意义,不要养成考试思维,看到问题就想解答,而是从建模可行性角度考虑,有可能建模吗?有确定回答的可能吗?
如果你有一把锤子,不要看到任何东西都当成钉子,别被高超的解决能力绑架了,如果用在错误的问题和场景上下文,解决问题的解决能力就是制造新问题,为啥一个bug修复带来更多bug呢?
衍生:无法争出对错的问题就回避,把它当成陷阱,躲过去,寻找更可能有确定性的问题去回答。抬杠也要选题,选题能力强才是真的强
https://www.jdon.com/69607.html
相关文章:

什么是拉宾-斯科特定理?
拉宾-斯科特定理(Rabin-Scott theorem )是数学上最深刻的数学结果之一。拉宾-斯科特定理是人们最喜欢的计算机科学概念之一。 当正确理解拉宾-斯科特定理时,它会以一种相当基本的方式改变你对现实的看法。然而,它典型的教科书式的呈现方式掩盖了这种深…...
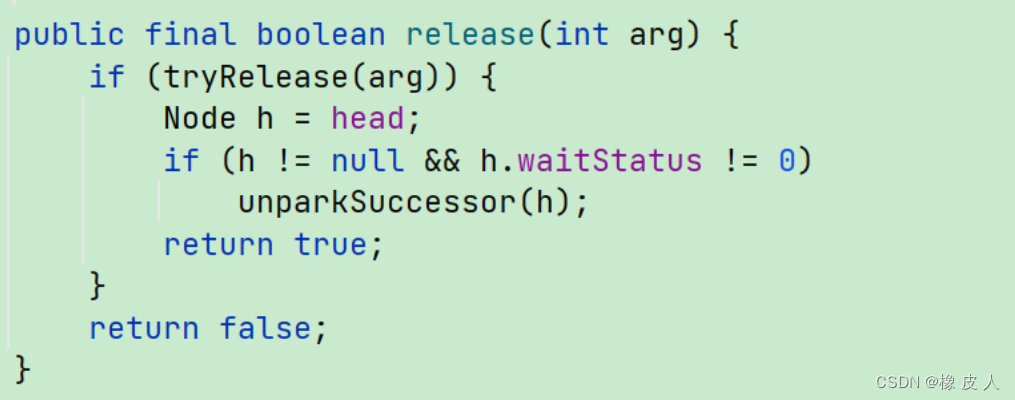
Java并发编程第11讲——AQS设计思想及核心源码分析
Java并发包(JUC)中提供了很多并发工具,比如前面介绍过的ReentrantLock、ReentrantReadWriteLock、CountDownLatch、Semaphore、FutureTask等锁或者同步部件,它们的实现都用到了一个共同的基类——AbstractQueuedSynchronizer&…...

什么是数据库?数据库有哪些基本分类和主要特点?
数据库是以某种有组织的方式存储的数据集合。本文从数据库的基本概念出发,详细解读了数据库的主要类别和基本特点,并就大模型时代备受瞩目的数据库类型——向量数据库进行了深度剖析,供大家在了解数据库领域的基本概念时起到一点参考作用。 …...

flutter显示出底部控件的引导页
需求:同一个页面的两个不同的入口,同一个控件的位置有变化,显示引导页时对应这个控件的引导内容的位置也需要改变;同时半透明底部显示出真实的页面内容。 这样的需要如果切图然后再往页面上贴位置无法精确的对准。 思路࿱…...

常用设计模式——模板方法模式
什么是模板方法模式 模板方法模式:定义一个操作中的算法的骨架,而将一些步骤延迟到子类中。模板方法使得子类可以不改变一个算法的结构即可重定义该算法的某些特定步骤。 主要解决:一些方法通用,却要在每一个子类都重写这些方法…...
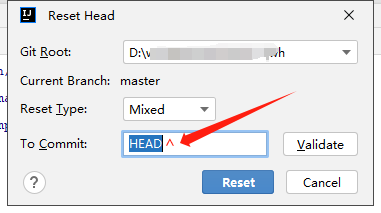
idea使用git删除本地提交(未推送)
1、找到reset head 2、打开弹窗,在HEAD后面输入^ 结果为HEAD^ 注释: Reset Type 有三种: Mixed(默认方式),保留本地源码,回退 commit 和 index 信息,最常用的方式Soft 回退到某个版本…...

centos 7部署Mysql8.0主从
Mysql官网中关于部署主从的网址 环境准备: 搭建虚拟机和安装Mysql之前的文章中已经涉及,在此不再赘述。 主从IPMysql账号密码主192.168.213.4root/Root1234!从192.168.213.5root/Root1234! 1、主数据库设置 配置my.cnf 一般存放于/etc/。 主从配…...

asp.net docker-compose添加es search
打开docker-compose.yml添加 es-search:image: docker.elastic.co/elasticsearch/elasticsearch:7.17.14 打开docker-compose.override.yml添加 es-search:volumes:- data01:/usr/share/elasticsearch/dataports:- 9200:9200 docker集群中添加es search成功...

工业路由器网关的网络协议之NAT技术
在物联网通讯领域,NAT技术能将内网的一个私有IP转换成一个公网IP去接入互联网,解决组建局域网络时私有IP地址无法在公网上进行路由的问题。 NAT(Network Address Translation)的三种方式: 静态NAT 1、一个私有IP对应…...

【亲测可用】SpringBoot使用Redis的Lettuce连接池报RedisCommandTimeoutException
目录 一、问题详情 二、根本原因 三、解决方案 一、问题详情 在最近新项目的开发当中,当项目刚启动的时候访问Redis服务一切正常,但是过了几分钟后再次访问Redis就报如下错误。 Redis command timed out; nested exception is io.lettuce.core.RedisCommandTimeoutExcept…...

When Urban Region Profiling Meets Large Language Models
本文是LLM系列文章,针对《When Urban Region Profiling Meets Large Language Models》的翻译。 当城市区域轮廓遇到大型语言模型时 摘要1 引言2 前言3 方法4 实验5 结论与未来工作 摘要 基于网络数据的城市区域概况对城市规划和可持续发展至关重要。我们见证了LL…...

【python】最大的偶数
题目: """ 给出一个由非负整数组成的序列 A (A1,A2,A3,....,Av)。这个序列的长度为N判断是否存在一个偶数可以表示为在A中两个不同元素的和。若存在,找到最大的偶数,否则输出”-…...

QT 实现两款自定义的温度计/湿度控件
文章目录 0 引入1、带有标尺的温度/湿度计控件1.头文件2.核心代码 2、竖起来的温度/湿度计控件1.头文件2.实现 3、引用 0 引入 QT原生控件没有实现如仪表盘或者温度计的控件,只好自己实现,文章代码部分参考引用的文章。直接上图 图一 带有标尺的温度计…...
Fourier分析导论——第4章——Fourier级数的一些应用(E.M. Stein R. Shakarchi)
第 4 章 傅里叶级数的一些应用 Fourier series and analogous expansions intervene very naturally in the general theory of curves and surfaces. In effect, this theory, conceived from the point of view of analysis, deals obviously with the study of arbitra…...

c语言使用fdk_aac库对aac音频解码为pcm
//示例为adts的aac流数据(adts数据可以每一包都可以独立解析不需要拼凑) //解码数据的采样率同解码前的采样率,如果不满足需求,需要对数据进行重采样 #include <aacdecoder_lib.h>int m_fd -1; int m_fd2 -1;void aac2pc…...

zustand管理工具--React
npm i zustand 1.函数参数必须返回一个对象 对象内部编写状态数据和方法 2.set是用来修改数据的专门方法必须调用它来修改数据 import { useEffect } from "react"; import { create } from "zustand";// 1. 创建store const goodsStore create((set) …...

Elasticsearch内存分析
文章目录 Elasticsearch JVM内存由哪些部分组成Indexing BufferNode Query CacheShard Request CacheField Data CacheSegments Cache查询 非堆内存内存压力mat分析es的jvm缓存监控 Elasticsearch JVM内存由哪些部分组成 官方建议Elasticsearch设置堆内存为32G,因为…...
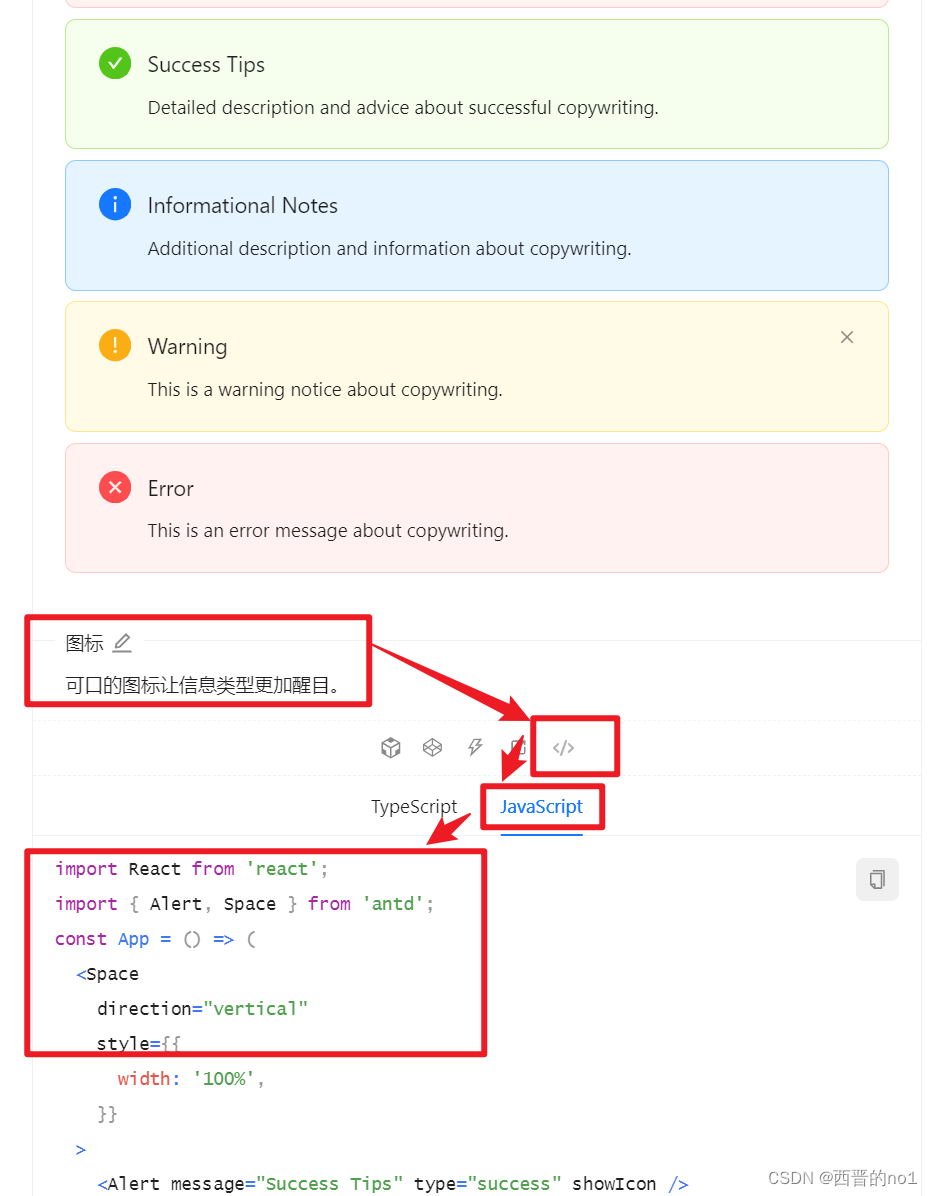
Alert警告提示(antd-design组件库)简单使用
1.Alert警告提示 警告提示,展现需要关注的信息。 2.何时使用 当某个页面需要向用户显示警告的信息时。 非浮层的静态展现形式,始终展现,不会自动消失,用户可以点击关闭。 组件代码来自: 警告提示 Alert - Ant Design 3…...
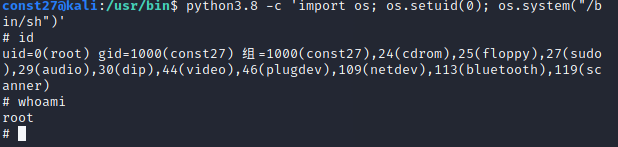
Linux提权方法总结
1、内核漏洞提权 利用内核漏洞提取一般三个环节:首先对目标系统进行信息收集,获取系统内核信息及版本信息 第二步,根据内核版本获取对应的漏洞以及exp 第三步,使用exp对目标进行攻击,完成提权 注:此处可…...

力扣第300题 最长递增子序列 c++ 动态规划题 附Java代码
题目 300. 最长递增子序列 中等 相关标签 数组 二分查找 动态规划 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
