线性代数(二)| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法
文章目录
- 1. 性质
- 1.1 重要性质梳理
- 1.1.1 转置和初等变换
- 1.1.2加法行列式可拆分
- 1.1.3 乘积行列式可拆分
- 1.2 行列式性质的应用
- 1.2.1 简化运算
- 1.2.2 将行列式转换为(二)中的特殊行列式
- 2 特殊行列式
- 2.1 上三角或下三角行列式
- 2.2 三叉行列式
- 2.3 行列式行和(列和)为定值
- 2.4 对称行列式和反对称行列式
- 2.5 范德蒙行列式
- 3.求行列式值的基本方法
- 3.1 行列式定义
- 3.2 行列式性质
- 3.3 行列式的展开
- 3.4 加边法
- 3.5 归纳法
方阵行列式包含着大量的信息
首先它直接告诉我们行列式是否可逆,如果为零则不可逆,如果不为零则可逆
它可
1. 性质
1.1 重要性质梳理
1.1.1 转置和初等变换
-
对于转置,值不变 | A T A^T AT|=| A A A|
-
对于交换行列式的任意两行,行列式值变号
可以证明若某两行相同,则行列式值为0
-
对于某一行(列)乘一个数K,等于给矩阵的行列式乘K
注意区别|kA|与 k|A| 其中 $|kA|=k^n|A| $ (A为n阶矩阵)
-
对于某一行(列)加上另一行(列)的k倍,行列式值不变
1.1.2加法行列式可拆分
行列式的某一行都为两项之和,可以拆分为两行项之和(和的那一行分开,其余行保持不变)。
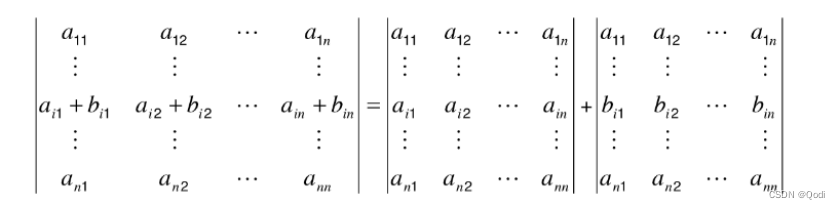
1.1.3 乘积行列式可拆分
设 A B 为n阶方阵,则|AB|=|A||B| 更一般的有|A1A2…As|=|A1||A2|…|As|
1.2 行列式性质的应用
1.2.1 简化运算
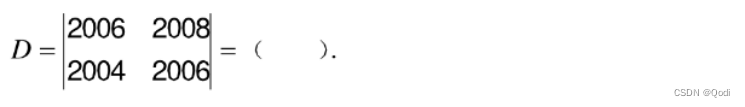
解: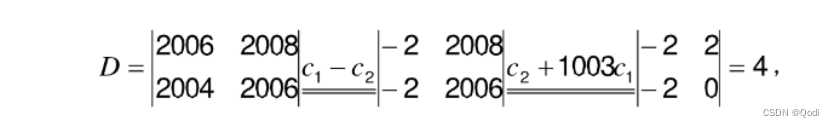
1.2.2 将行列式转换为(二)中的特殊行列式
通过行列式变换转换为特殊行列式
2 特殊行列式
2.1 上三角或下三角行列式
行列式的值为对象线上的元素的乘积,这个可以用行列式的定义来证明,它是一个很重要的行列式,三叉行列式,或者是行列式和为定值的行列式最后本质上都转为了这个特殊行列式
例:
∣ 1 1 2 3 0 − 1 1 7 0 0 3 2 0 0 0 4 ∣ = 1 × − 1 × 3 × 4 = − 12 \begin{vmatrix}1&1&2&3&\\0&-1&1&7\\0&0&3&2\\0&0&0&4\end{vmatrix}=1×-1×3×4=-12 10001−10021303724 =1×−1×3×4=−12
2.2 三叉行列式
本质上需要转换为1 中的上三角或下三角行列式 KP88 1T
例:计算n阶行列式 ∣ 1 1 1 ⋯ 1 − 1 2 0 ⋯ 0 − 1 0 3 ⋱ ⋮ ⋮ ⋮ ⋱ ⋱ 0 − 1 0 ⋯ 0 n ∣ \begin{vmatrix}1&1&1&\cdots&1\\-1&2&0&\cdots&0\\-1&0&3&\ddots&\vdots\\\vdots&\vdots&\ddots&\ddots&0\\-1&0&\cdots&0&n\end{vmatrix} 1−1−1⋮−1120⋮0103⋱⋯⋯⋯⋱⋱010⋮0n
解:解决办法就是把主对角线下(上)的元素都变为零,对于本题的话,左下角都为-1,因而可以把第二列乘二分之一加到第一列上去,第三列乘三分之一加到第一列上去……可以得到如下 ∣ 1 + 1 2 + 1 3 + . . . + 1 n 1 1 ⋯ 1 0 2 0 ⋯ 0 0 0 3 ⋱ ⋮ ⋮ ⋮ ⋱ ⋱ 0 0 0 ⋯ 0 n ∣ \begin{vmatrix}1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}&1&1&\cdots&1\\0&2&0&\cdots&0\\0&0&3&\ddots&\vdots\\\vdots&\vdots&\ddots&\ddots&0\\0&0&\cdots&0&n\end{vmatrix} 1+21+31+...+n100⋮0120⋮0103⋱⋯⋯⋯⋱⋱010⋮0n
进而采用主对角线上元素相乘即可得到结果 n ! ( 1 + 1 2 + 1 3 + . . . + 1 n ) n! (1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}) n!(1+21+31+...+n1)
2.3 行列式行和(列和)为定值
如果行和或者列和为定值时,一般采取的方法是将各行(列)加到某一行(列),提取公因式
例:
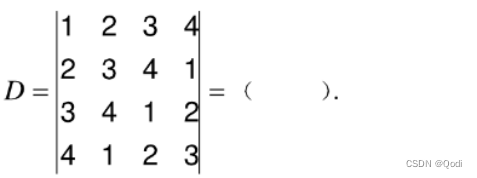
解:

2.4 对称行列式和反对称行列式
(1)反对称行列式 主对角线上全为零,主对角上下对应元素相反
如: ∣ 0 1 2 − 1 0 3 − 2 − 3 0 ∣ \begin{vmatrix}0&1&2 \\-1&0&3\\-2&-3&0\end{vmatrix} 0−1−210−3230 反对称行列式有一个重要性质 A T = − A A^T=-A AT=−A 基于这一性质,我们可以推出若反对称行列式为奇数阶 ,则行列式值为零,左面这个行列式即为零 ,证明 因为 A T = − A A^T=-A AT=−A 所以 ∣ A T ∣ = ∣ − A ∣ = ( − 1 ) n ∣ A ∣ |A^T|=|-A|=(-1)^n|A| ∣AT∣=∣−A∣=(−1)n∣A∣ 当n为奇数,则有 ∣ A T ∣ = − ∣ A ∣ |A^T|=-|A| ∣AT∣=−∣A∣ 又因为转置行列式值不变 ,所以 ∣ A ∣ = − ∣ A ∣ |A|=-|A| ∣A∣=−∣A∣ 则|A|只能为0
(2)对称行列式 主对角线上元素无要求,主对角上下对应元素相等
如: ∣ 1 1 2 1 2 3 2 3 0 ∣ \begin{vmatrix}1&1&2 \\1&2&3\\2&3&0\end{vmatrix} 112123230
2.5 范德蒙行列式
范德蒙行列式
3.求行列式值的基本方法
3.1 行列式定义
用行列式定义求的矩阵具有较多的零元素的特征,相应元素取过之后所在列所在行就不能再取元素了
例1 求A= ∣ 1 1 0 0 2 − 1 0 0 0 0 3 0 0 0 4 4 ∣ \begin{vmatrix}1&1&0&0&\\2&-1&0&0\\0&0&3&0\\0&0&4&4\end{vmatrix} 12001−10000340004
解: A=1×(-1)×3×4+(-1)×1×2×3×4=-36
拓展C P9 1T 3T
3.2 行列式性质
利用(一)中的行列式性质,如加法行列式可拆性,基本变换等结合一些行列式两行成比例结果为零的一些推论
例2 求A= ∣ a 2 ( a + 1 ) 2 ( a + 2 ) 2 ( a + 3 ) 2 b 2 ( b + 1 ) 2 ( b + 2 ) 2 ( b + 3 ) 2 c 2 ( c + 1 ) 2 ( c + 2 ) 2 ( c + 3 ) 2 d 2 ( d + 1 ) 2 ( d + 2 ) 2 ( d + 3 ) 2 ∣ \begin{vmatrix}a^2&(a+1)^2&(a+2)^2 &(a+3)^2\\b^2&(b+1)^2&(b+2)^2 &(b+3)^2\\c^2&(c+1)^2&(c+2)^2 &(c+3)^2\\d^2&(d+1)^2&(d+2)^2 &(d+3)^2\\\end{vmatrix} a2b2c2d2(a+1)2(b+1)2(c+1)2(d+1)2(a+2)2(b+2)2(c+2)2(d+2)2(a+3)2(b+3)2(c+3)2(d+3)2
解: ∣ a 2 ( a + 1 ) 2 ( a + 2 ) 2 ( a + 3 ) 2 b 2 ( b + 1 ) 2 ( b + 2 ) 2 ( b + 3 ) 2 c 2 ( c + 1 ) 2 ( c + 2 ) 2 ( c + 3 ) 2 d 2 ( d + 1 ) 2 ( d + 2 ) 2 ( d + 3 ) 2 ∣ \begin{vmatrix}a^2&(a+1)^2&(a+2)^2 &(a+3)^2\\b^2&(b+1)^2&(b+2)^2 &(b+3)^2\\c^2&(c+1)^2&(c+2)^2 &(c+3)^2\\d^2&(d+1)^2&(d+2)^2 &(d+3)^2\\\end{vmatrix} a2b2c2d2(a+1)2(b+1)2(c+1)2(d+1)2(a+2)2(b+2)2(c+2)2(d+2)2(a+3)2(b+3)2(c+3)2(d+3)2 = ∣ a 2 a 2 + 2 a + 1 a 2 + 4 a + 4 a 2 + 6 a + 9 b 2 b 2 + 2 b + 1 b 2 + 4 b + 4 b 2 + 6 b + 9 c 2 c 2 + 2 c + 1 c 2 + 4 c + 4 c 2 + 6 c + 9 d 2 d 2 + 2 d + 1 d 2 + 4 d + 4 d 2 + 6 d + 9 ∣ \begin{vmatrix}a^2&a^2+2a+1&a^2+4a+4 &a^2+6a+9\\b^2&b^2+2b+1&b^2+4b+4 &b^2+6b+9\\c^2&c^2+2c+1&c^2+4c+4 &c^2+6c+9\\d^2&d^2+2d+1&d^2+4d+4 &d^2+6d+9\\\end{vmatrix} a2b2c2d2a2+2a+1b2+2b+1c2+2c+1d2+2d+1a2+4a+4b2+4b+4c2+4c+4d2+4d+4a2+6a+9b2+6b+9c2+6c+9d2+6d+9
将右边完全拆开后,一共有3×3×3=27种组合相加,但每种组合总会有成比例的两列,因而最后行列式=0
3.3 行列式的展开
行列式的展开本质是降阶,是一种非常重要的方法,降阶的话有可以得到二阶三阶行列式方便计算,或者是我们可以得到一种递推关系式(n阶矩阵)
(1)如 ∣ 1 1 3 0 2 − 1 1 0 5 6 3 0 1 2 4 4 ∣ \begin{vmatrix}1&1&3&0&\\2&-1&1&0\\5&6&3&0\\1&2&4&4\end{vmatrix} 12511−16231340004 可按最后一列展开,则可以直接降解为三阶行列式,我们发现某一行(列)的零越多越好,多一个零就少算一个行列式。
有时候某一列的零不是很多,但是我们又没有其他好的方法计算,我们可以先进行一些变换,使得某一列或某一行的零变多,进而简化运算,如要求 ∣ 1 1 3 1 2 − 1 1 2 5 6 3 3 1 2 4 4 ∣ \begin{vmatrix}1&1&3&1&\\2&-1&1&2\\5&6&3&3\\1&2&4&4\end{vmatrix} 12511−16231341234 我们可以先用第二行减去二倍的第一行,第三行减去三倍的第一行,第四行减去四倍的第一行,得到 ∣ 1 1 3 1 0 − 3 − 5 0 2 3 − 6 0 − 3 − 2 − 8 0 ∣ \begin{vmatrix}1&1&3&1&\\0&-3&-5&0\\2&3&-6&0\\-3&-2&-8&0\end{vmatrix} 102−31−33−23−5−6−81000 按最后一列展开即可降阶为三阶**-** ∣ 0 − 3 − 5 2 3 − 6 − 3 − 2 − 8 ∣ \begin{vmatrix}0&-3&-5&\\2&3&-6&\\-3&-2&-8\end{vmatrix} 02−3−33−2−5−6−8 记得前面的负号不要丢掉,再按第一列展开即可得到两个二阶行列式
(2)对于n阶矩阵,我们不可能降阶到二阶三阶,但是我们可以找到递推关系式进而求出答案
3.4 加边法
基于行列式展开让行列式升阶
3.5 归纳法
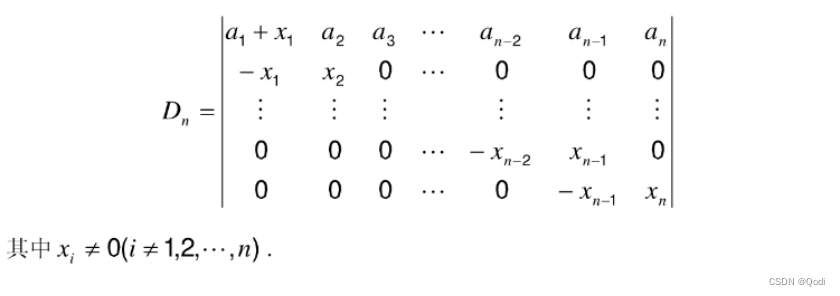
解:

相关文章:

线性代数(二)| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法
文章目录 1. 性质1.1 重要性质梳理1.1.1 转置和初等变换1.1.2加法行列式可拆分1.1.3 乘积行列式可拆分 1.2 行列式性质的应用1.2.1 简化运算1.2.2 将行列式转换为(二)中的特殊行列式 2 特殊行列式2.1 上三角或下三角行列式2.2 三叉行列式2.3 行列式行和&…...

OpenCV入门7:图像形态学变换
形态学是一种针对图像形状和结构进行操作和分析的图像处理方法。在OpenCV中,提供了一些函数和方法用于执行形态学操作。下面将介绍一些常见的形态学操作及其在OpenCV中的实现方式。 膨胀(Dilation): 膨胀操作可以扩展图像中的边…...

Apache Storm 2.5.0 集群安装与配置
1、下载Apache Storm 2.5.0 https://mirrors.tuna.tsinghua.edu.cn/apache/storm/apache-storm-2.5.0/ 2、准备3台服务器 192.168.42.139 node1 192.168.42.140 node1 192.168.42.141 node2 3、配置host [rootnode1 ~]# cat /etc/hosts 127.0.0.1 localhost localhost…...

Android-将编码的base64图像,添加水印,转换成File存储到手机
一、将图片file转换成bitmap Bitmap bitmap = BitmapFactory.decodeFile(file.getAbsolutePath()); 二、给图片添加水印 String[] content = new String[]{"纬度:" + latitude, "经度:" + longitude, "地址:" + signAddress, "时间:&…...
AI 绘画 | Stable Diffusion 图生图
图生图简介 Stable Diffusion 不仅可以文生图,还可以图生图。文生图就是完全用提示词文本去生成我们想要图片,但是很多时候会有词不达意的感觉。就像我们房子装修一样,我们只是通过文字描述很难表达出准确的想要的装修效果,如果能…...
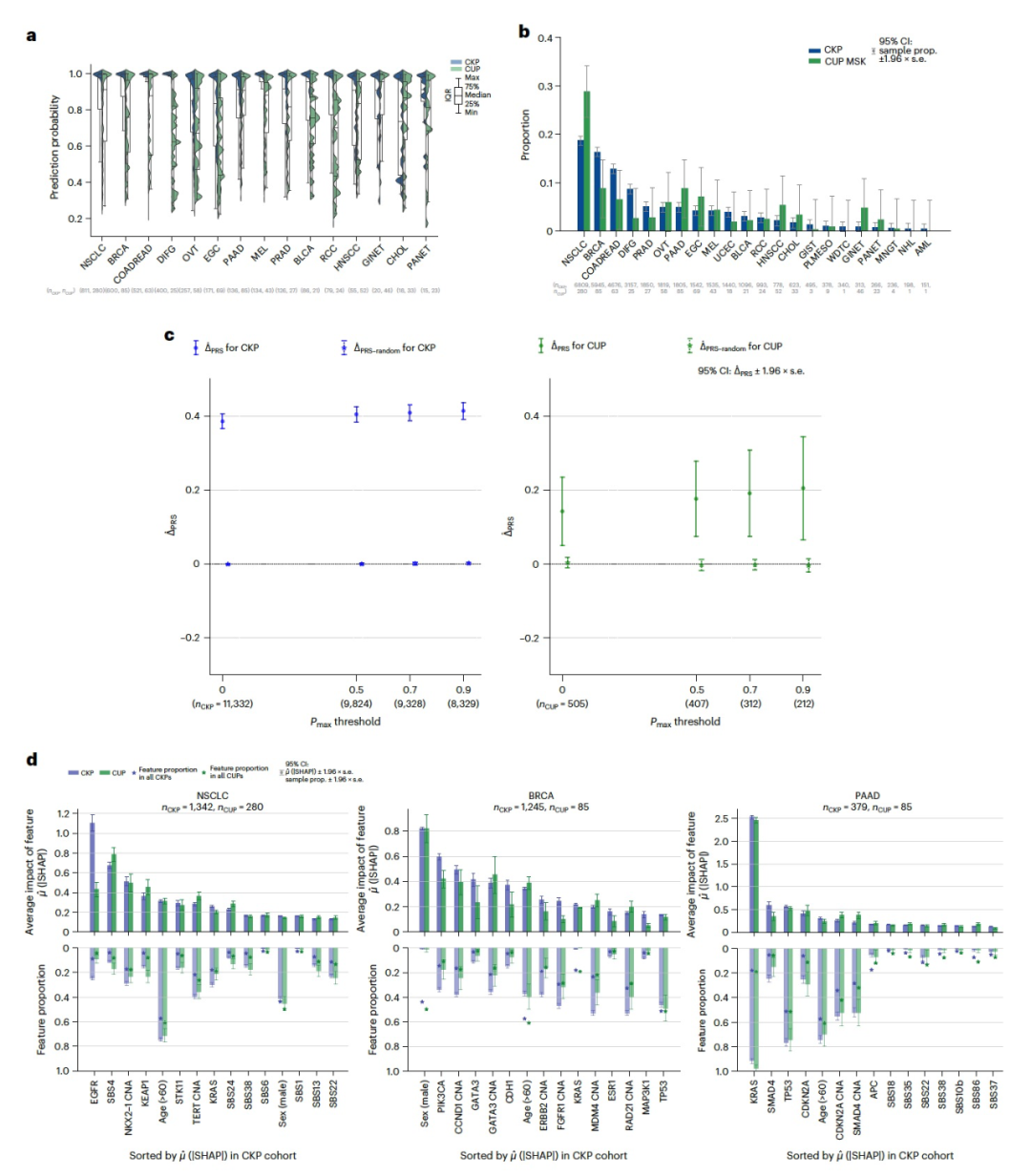
Nat. Med. | 基于遗传学原发部位未知癌症的分类和治疗反应预测
今天为大家介绍的是来自Alexander Gusev团队的一篇论文。原发部位未知癌症(Cancer of unknown primary,CUP)是一种无法追溯到其原发部位的癌症,占所有癌症的3-5%。CUP缺乏已建立的靶向治疗方法,导致普遍预后…...

RocketMQ如何安全的批量发送消息❓
优点: 批量发送消息可以提高rocketmq的生产者性能和吞吐量。 使用场景: 发送大量小型消息时;需要降低消息发送延迟时;需要提高生产者性能时; 注意事项: 消息列表的大小不能超过broker设置的最大消息大小;消息列表…...

计算机视觉与深度学习 | 基于视觉惯性紧耦合的SLAM后端优化算法
===================================================== github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ===================================================== 基于视觉惯性紧耦合的SLAM后端优化算法 引言视觉惯性联合初始化非线性优…...

GDI+ 绘制透明图
目录 一、GDI+ 准备工作 1、线程中添加GDI+支持 2、Gdiplus::Bitmap 1)、从文件创建位图...

【Java】IntelliJ IDEA使用JDBC连接MySQL数据库并写入数据
目录 0 准备工作1 创建Java项目2 添加JDBC 驱动程序3 创建数据库连接配置文件4 创建一个 Java 类来连接和操作数据库5 运行应用程序 在 IntelliJ IDEA 中连接 MySQL 数据库并将数据存储在数据表中,使用 Java 和 JDBC(Java Database Connectivity…...

Linux Hadoop平台伪分布式安装
Linux Hadoop 伪分布式安装 1. JDK2. Hadoop3. MysqlHive3.1 Mysql8安装3.2 Hive安装 4. Spark4.1 Maven安装4.2 Scala安装4.3 Spark编译并安装 5. Zookeeper6. HBase 版本概要: jdk: jdk-8u391-linux-x64.tar.gzhadoop:hadoop-3.3.1.tar.gzh…...
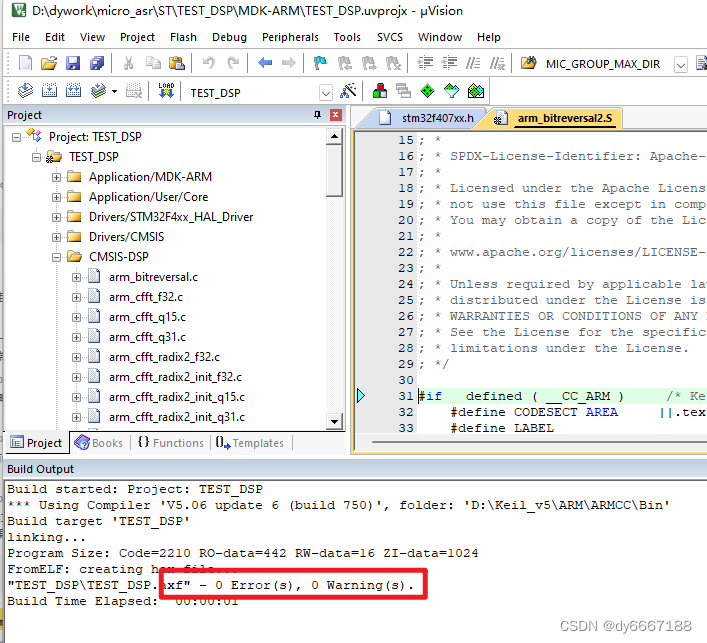
【STM32-DSP库的使用】基于Keil5 + STM32CubeMX 手动添加、库添加方式
STM32-DSP库的使用 一.CMSIS-DSP1.1 DSP库简介1.2 支持的函数类别1.3 宏定义 二、操作2.1 STM32CubeMX 配置基本工程2.2 Lib库的方式实现(推荐)2.3 手动添加DSP文件(可以下载官方最新库,功能齐全) 三、MFCC测试DSP加速效果 为验证语音识别MFC…...
createElement的用法
目录 一:介绍 二:语法与例子 1、语法 2、一些例子 例1: 例2: 例3: 3、第二种写法 一:介绍 document.createElement()是在对象中创建一个对象,要与appendChild() 或 insertBefore()方法…...
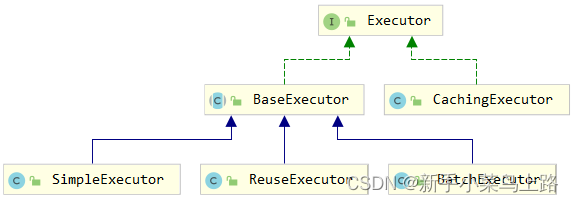
Mabitys总结
一、ORM ORM(Object/Relation Mapping),中文名称:对象/关系 映射。是一种解决数据库发展和面向对象编程语言发展不匹配问题而出现的技术。 使用JDBC技术时,手动实现ORM映射: 使用ORM时,自动关系映射: &am…...
JAVA安全之Log4j-Jndi注入原理以及利用方式
什么是JNDI? JDNI(Java Naming and Directory Interface)是Java命名和目录接口,它提供了统一的访问命名和目录服务的API。 JDNI主要通过JNDI SPI(Service Provider Interface)规范来实现,该规…...
Spring源码系列-框架中的设计模式
简单工厂 实现方式: BeanFactory。Spring中的BeanFactory就是简单工厂模式的体现,根据传入一个唯一的标识来获得Bean对象,但是否是在传入参数后创建还是传入参数前创建这个要根据具体情况来定。 实质: 由一个工厂…...
数据的读取和保存-MATLAB
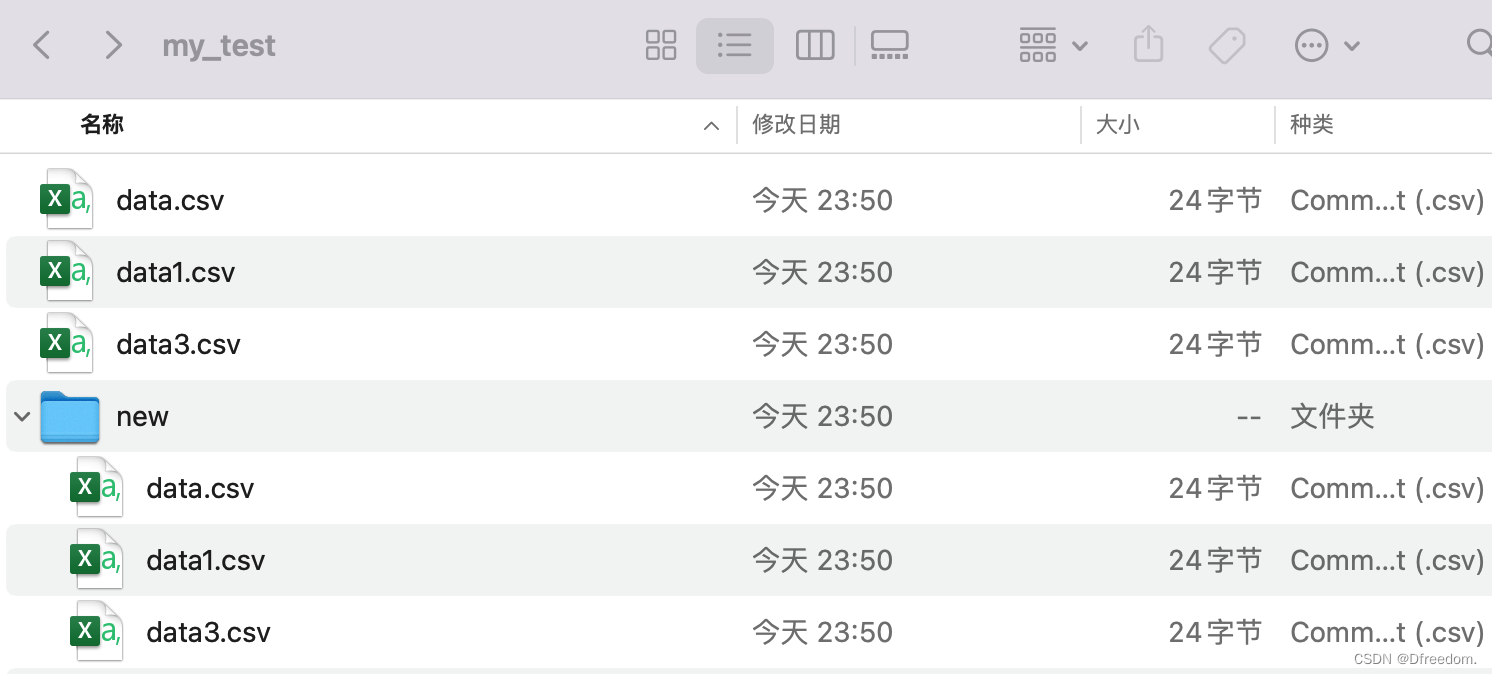
1 序言 在进行数据处理时,经常需要写代码对保存在文件中的数据进行读取→处理→保存的操作,流程图如下: 笔者每次在进行上述操作时,都需要百度如何“选中目标文件”以及如何“将处理好的数据保存到目标文件中”,对这一…...

C++ 输入、输出和整数运算
【问题描述】 编写一个程序,读入两个整数,计算并输出他们的和、积、商和余数。 【输入形式】 程序运行到输入时,不要显示输入提示信息。 输入为两个整数(在问题描述中记作A和B,程序中请自定变量名),A和B使…...

Element Plus 解决组件显示英文问题
要解决Element Plus日历组件显示英文的问题,可以使用Element Plus提供的国际化功能,切换成中文语言。下面是一个简单的示例: 首先,在main.ts或者你的入口文件中引入Element Plus的中文语言包和Vue I18n: import { cr…...
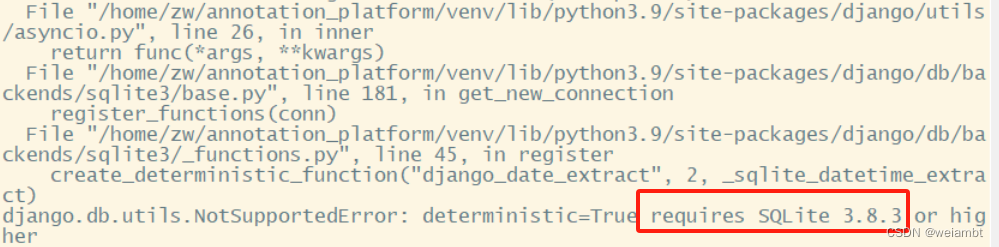
sqlite3.NotSupportedError: deterministic=True requires SQLite 3.8.3 or higher
问题描述 sqlite3.NotSupportedError: deterministicTrue requires SQLite 3.8.3 or higher 解决方法 A kind of solution is changing the database from sqlite3 to pysqlite3. After acticate the virtualenv, install pysqlite. pip3 install pysqlite3 pip3 install …...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
