leetcode做题笔记216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7 输出: [[1,2,4]] 解释: 1 + 2 + 4 = 7 没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]] 解释: 1 + 2 + 6 = 9 1 + 3 + 5 = 9 2 + 3 + 4 = 9 没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1 输出: [] 解释: 不存在有效的组合。 在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
思路一:回溯
c++解法
class Solution {
public:vector<int> samp;vector<vector<int>> ans;void dfs(int k,int n,int cur){if (samp.size()==k)if(n==0) {ans.push_back(samp);return;}else return;if (cur>9||cur>n) return;samp.push_back(cur);dfs(k,n-cur,cur+1);samp.pop_back();dfs(k,n,cur+1);}vector<vector<int>> combinationSum3(int k, int n) {dfs(k,n,1);return ans;}
};分析:
本题要求出组合总和等于目标数的所有组合,利用回溯当组合总和大于目标数则结束遍历,不断回溯找出所有组合
总结:
本题考察对回溯的运用,不断枚举得到所有组合
相关文章:

leetcode做题笔记216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件: 只使用数字1到9每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。 示例 1: 输入: k 3, n 7 输出: [[1,2,4]] 解释…...
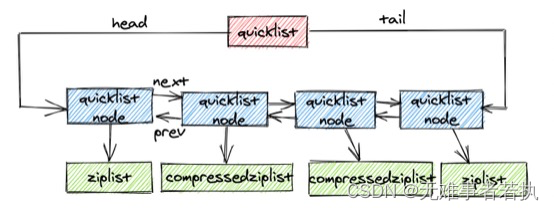
Redis系列-Redis数据类型【3】
目录 Redis系列-Redis数据类型【3】字符串类型(String)SDS (simple dynamic string) 哈希类型(Hash)列表类型(List)集合类型(Set)有序集合类型(ZSet)字符串类…...
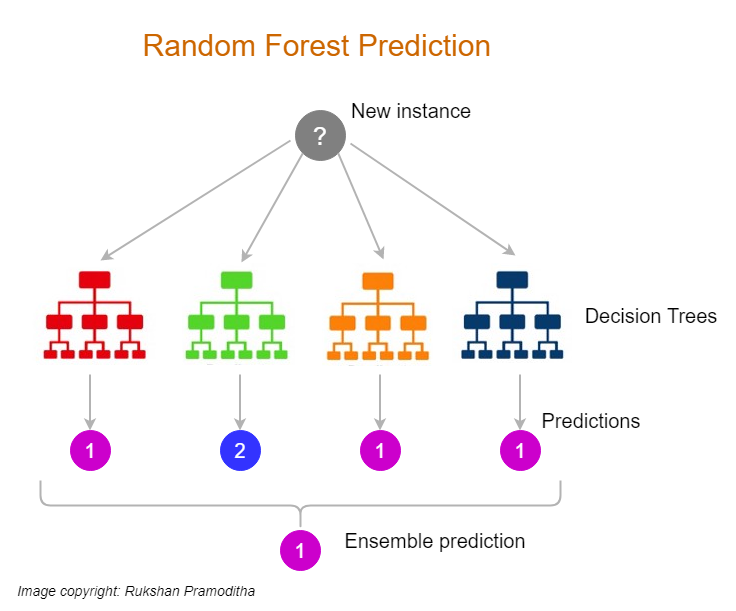
机器学习 - 决策树:技术全解与案例实战
目录 一、引言二、决策树基础决策树模型概述构建决策树的关键概念特征选择决策树的生成 决策树的剪枝 三、算法研究进阶提升树和随机森林提升树(Boosted Trees)随机森林(Random Forests) 进化算法与决策树决策树结构的进化 多目标…...

Opus 1.4 编译脚本
Opus 1.4 编译脚本 官网地址:https://www.opus-codec.org/ 仓库地址:https://gitlab.xiph.org/xiph/opus #!/bin/bash# 每次编译删除原来的编译文件 rm build -rf rm install -rf # 创建临时编译目录,避免污染源文件 mkdir build # 定义一…...
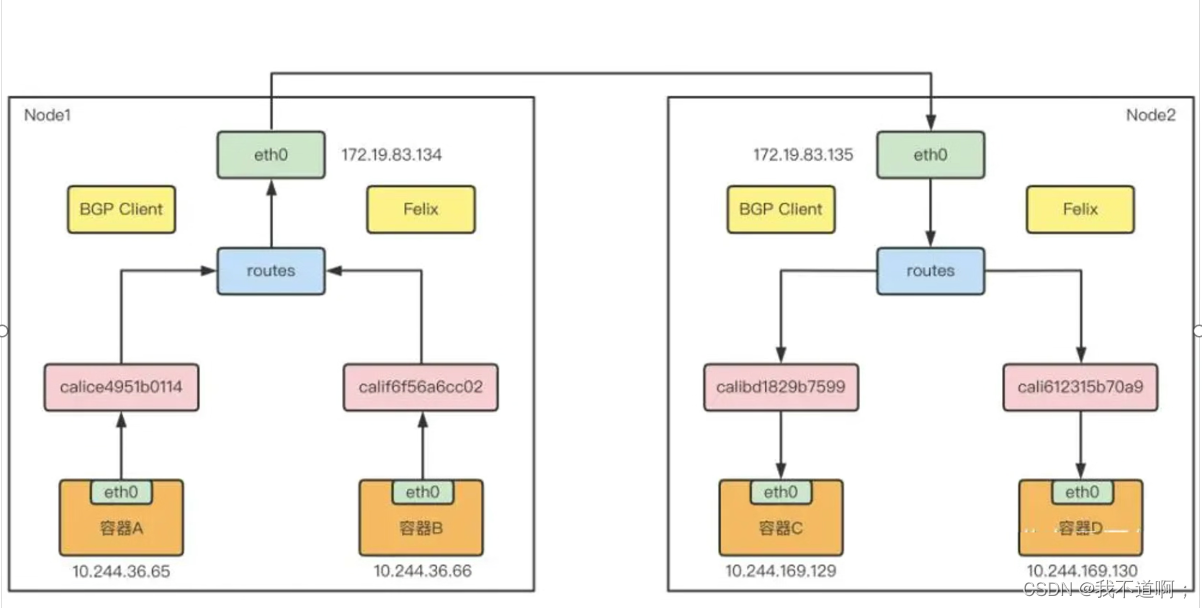
二进制搭建及高可用 Kubernetes v1.20
目录 一、实验规划: 二、操作系统初始化配置: 1. 关闭防火墙 selinux: 2. 关闭swap分区: 3. 根据规划设置主机名: 4. 所有主机添加hosts: 5. 调整内核参数: 6. 时间同步: 三、部署 etcd 集群:…...

SpringBoot 使用WebSocket打造在线聊天室
1、WebSocket是HTML5开始提供的一种在单个 TCP 连接上进行全双工通讯的协议。在WebSocket API中,浏览器和服务器只需要做一个握手的动作,然后,浏览器和服务器之间就形成了一条快速通道。两者之间就直接可以数据互相传送。 2、浏览器通过 Java…...

vcpkg安装第三方库,报错fatal error RC1107: invalid usage; use RC /? for Help
记录一下,vcpkg不知道什么原因安装库失败。 首先就是原本安装过的库,再次安装之后。不知道环境哪里修改了。会导致安装报错。 Change Dir: D:/Software/vcpkg/buildtrees/freeglut/x64-windows-dbgRun Build Command(s): "D:/Program Files/Micros…...

axios的介绍及配置多个服务器url
文章目录 1、常用的默认配置的是:baseURL、method、timeout2、axios配置多个服务器url3、配置api文件4、文件中使用 1、常用的默认配置的是:baseURL、method、timeout ① baseURL:设置url的基本结构(请求根地址)&…...
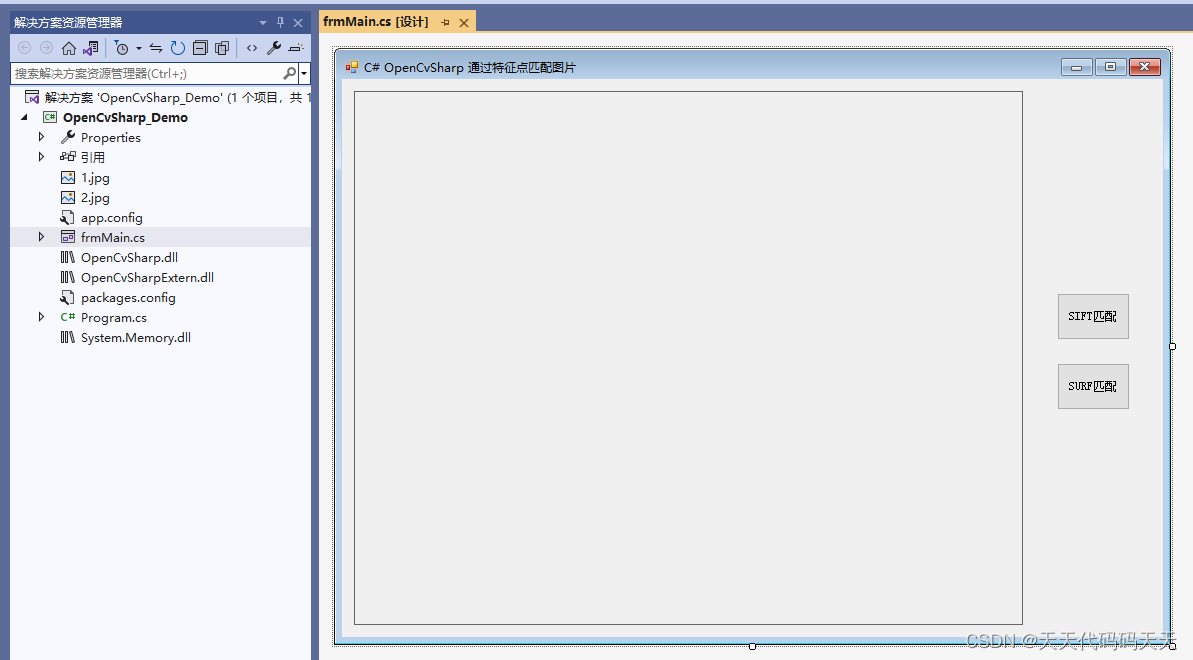
C# OpenCvSharp 通过特征点匹配图片
SIFT匹配 SURF匹配 项目 代码 using OpenCvSharp; using OpenCvSharp.Extensions; using System; using System.Collections.Generic; using System.Drawing; using System.Linq; using System.Text.RegularExpressions; using System.Windows.Forms; using static System.Net…...

10个python爬虫入门实例
昨天带伙伴学习python爬虫,准备了几个简单的入门实例,涉及主要知识点: web是如何交互的 requests库的get、post函数的应用 response对象的相关函数,属性 python文件的打开,保存 代码中给出了注释,并且…...
麒麟KYLINOS命令行设置系统静音
原文链接:麒麟KYLINOS命令行设置系统静音 hello,大家好啊,今天给大家带来一篇在麒麟KYLINOS上使用命令行调节系统静音的方法,有时候需要制作模板,便可以采用此方法,话不多说,一起来看看吧。 1、…...

零信任安全:构建无懈可击的网络防护体系
随着网络技术的飞速发展,信息安全问题日益凸显,传统的安全防护手段已经无法满足复杂多变的安全需求。在此背景下,零信任安全模型逐渐受到广泛关注。本文将探讨零信任安全的概念、优势以及如何构建无懈可击的网络防护体系。 一、零信任安全概念…...

华为李鹏:到 2025 年智能算力需求将达到目前水平的 100 倍
在第十四届全球移动宽带论坛上,华为高级副总裁、运营商 BG 总裁李鹏表示,大模型为代表的 AI 应用发展带来对智能算力的爆发式需求。 李鹏在题为《加速 5G 商业正循环,拥抱更繁荣的 5.5G》的讲话中表示,「5G 已经走在商业成功的正确…...

【漏洞复现】深信服下一代防火墙NGAF存在任意文件上传漏洞 附POC
漏洞描述 深信服下一代防火墙(Next-Generation Application Firewall)NGAF是面向应用层设计,能够精确识别用户、应用和内容,具备完整安全防护能力,能够全面替代传统防火墙,并具有强劲应用层处理能力的全新网络安全设备。NGAF解决了传统安全设备在应用识别、访问控制、内…...

城市内涝积水预防,万宾科技内涝监测仪如何预警?
近几年来城市内涝所引发的安全隐患极为突出,影响着城市道路安全,而且也让市民心中多有惶恐。一旦城市内涝问题出现背后不仅是路面积水问题,更会导致城市无法正常运行,导致市民日常生活和工作受到影响。所以对于排水防涝设施的建设…...

SpringBoot定时任务打成jar 引入到新的项目中后并自动执行
一、springBoot开发定时任务 ①:连接数据库实现新增功能 1. 引入依赖 <dependency><groupId>org.projectlombok</groupId><artifactId>lombok</artifactId><optional>true</optional> </dependency> <dependen…...
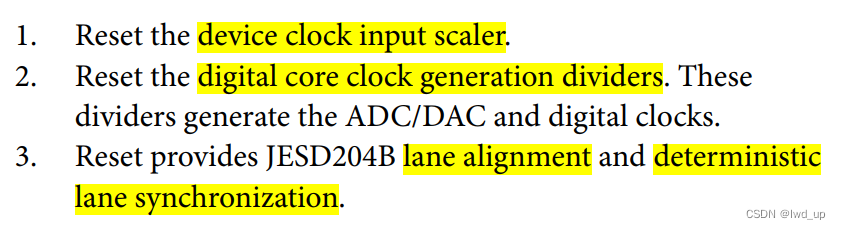
AD9371 官方例程 NO-OS 主函数 headless 梳理(一)
AD9371 系列快速入口 AD9371ZCU102 移植到 ZCU106 : AD9371 官方例程构建及单音信号收发 ad9371_tx_jesd -->util_ad9371_xcvr接口映射: AD9371 官方例程之 tx_jesd 与 xcvr接口映射 AD9371 官方例程 时钟间的关系与生成 : AD9371 官方…...
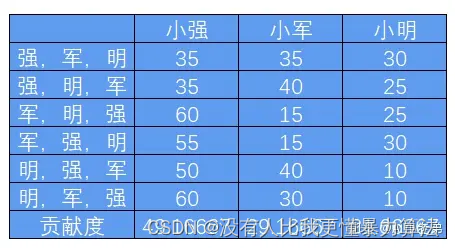
SHAP 和 LIME 解释模型
内容大纲 1、SHAP 解释器1.1 案例:用于预测患者肺癌1.2 案例中使用的shap解释器1.3 SHAP工作原理1.4 举例说明 2、LIME 解释器2.1 案例:判断法律案件胜诉可能性2.2 LIME解释器工作原理2.3 本地解释模型的训练过程2.4 举例说明1:新闻分类2.4 举…...
若依vue-初步下载使用
若依框架可以满足大部分的后台管理系统的开发,使用频率也是比较高的,所以这里讲一下如何使用若依框架 若依框架代码克隆 首先去若依官网 http://www.ruoyi.vip/ 这里演示的是若依-vue版本的使用 我们点击下载 会跳转到码云仓库 或者直接点击下面的链接去码云仓库 https://git…...

Android 使用.9图 NinePatchDrawable实现动态聊天气泡
最近一段时间,在做一个需求,需要实现一个聊天气泡的动画效果,如下图所示: GitHub源码demo ,建议下载demo,运行查看。 动态聊天气泡动画 静态聊天气泡 经过一段时间调研,实现方案如下: 实现方…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
