【chatgpt问答记录】双端队列、栈和函数调用栈
collections.deque和queue.Queue的区别
Q:collections.deque()跟queue.Queue()有什么区别?
collections.deque() 和 queue.Queue 是两种不同的数据结构,它们有一些区别:
-
实现方式:
collections.deque()是 Python 标准库提供的双端队列数据结构,使用双向链表实现,具有高效的在两端进行添加和弹出操作。queue.Queue是 Python 标准库中的队列数据结构,通常用于多线程或多进程的并发编程,它提供线程安全的队列操作。
-
线程安全:
collections.deque()不是线程安全的,如果多个线程同时访问一个collections.deque对象,需要手动处理线程同步问题。queue.Queue是线程安全的,它提供了锁机制,可以在多线程环境中安全地进行入队和出队操作。
-
功能:
collections.deque()主要用于实现双端队列,适用于单线程环境,常用于快速添加和删除队列两端的元素。queue.Queue用于实现线程安全的队列,适用于多线程环境,可以在多个线程之间安全地共享数据。
在你的示例中,collections.deque() 用于实现中序遍历结果的存储,这是因为在这种情况下线程安全性并不是一个关键问题。如果在多线程环境中需要处理队列,那么通常会选择使用 queue.Queue 或其他线程安全的队列数据结构。
Q:两者的数据结构都是双端队列吗?
collections.deque() 和 queue.Queue 都可以用于实现队列,但它们的底层数据结构略有不同。
-
collections.deque()是基于双向链表实现的双端队列,允许在队列的两端进行高效的添加和删除操作。这使它非常适合用作普通队列或栈的实现,但它不是线程安全的。 -
queue.Queue通常是基于列表或数组实现的队列,但它提供了线程安全的操作,以便多个线程可以安全地对队列进行入队和出队操作。这是它的主要区别,因为它引入了锁机制以保证线程安全性。
所以,虽然它们都可以用于队列操作,但它们的设计目标和线程安全性不同。如果你只在单线程环境中使用队列,通常使用 collections.deque() 就足够了。如果需要在多线程环境中共享队列,那么 queue.Queue 提供了线程安全的解决方案。
递归、栈和函数调用栈
Q:递归函数的返回值是None啊,怎么回溯?
递归函数的返回值并不总是None,它取决于递归函数的设计和应用。在二叉树中序遍历的递归算法中,递归函数不一定需要返回值,它的主要目的是遍历树的节点,而不是计算某个特定值。通常,我们使用递归函数来访问树的节点并执行某些操作,例如将节点的值添加到结果列表中。
在中序遍历算法中,递归函数的返回值通常为空(或None,具体取决于编程语言),因为我们只是遍历树的节点并记录节点的值。遍历的过程是自然地根据递归的调用顺序来进行的,而不需要显式地处理返回值。递归函数的"回溯"是通过函数调用的栈来自动处理的。当递归函数返回时,控制会自动返回到上一个调用的函数,这样就实现了回溯过程。
如果递归函数需要返回某些值,例如计算树的高度或某个特定值,那么它会在返回时返回这些值。但在中序遍历算法中,通常不需要返回值,只需要记录访问的节点值即可。
Q:“递归函数的"回溯"是通过函数调用的栈来自动处理的。当递归函数返回时,控制会自动返回到上一个调用的函数,这样就实现了回溯过程。”这个可以详细举例再解释一下吗?
当递归函数执行时,每个函数调用都会在调用栈(call stack)中创建一个帧(frame),帧中包含了函数的局部变量、参数和执行位置。这样,递归函数可以在不同的层次上调用自身。
让我们通过一个示例来详细解释递归函数的"回溯"和如何通过调用栈来实现它。考虑以下递归函数,用于计算一个整数的阶乘:
def factorial(n):if n == 0:return 1else:return n * factorial(n - 1)
现在,让我们计算 factorial(5),即 5 的阶乘。函数调用栈的过程如下:
- 最初的调用是
factorial(5)。因为n不等于 0,所以它进入else分支,并调用factorial(4)。 - 在调用
factorial(4)之后,同样的过程继续,它会调用factorial(3),然后factorial(2),最后factorial(1)。 - 当
factorial(1)返回时,它返回的结果是 1。 - 现在,
factorial(2)可以计算为2 * 1,返回结果 2。 - 然后,
factorial(3)可以计算为3 * 2,返回结果 6。 - 最后,
factorial(4)可以计算为4 * 6,返回结果 24。 - 最初的调用
factorial(5)最终可以计算为5 * 24,返回结果 120。
在这个过程中,每个递归调用都会在调用栈中创建一个帧,该帧包含了当前函数的状态,包括局部变量 n 的值和执行位置。当递归函数返回时,控制会自动从当前函数的帧返回到调用该函数的上一个函数,然后继续执行。这就是"回溯"的过程,其中控制从调用栈的顶部向下返回。这种回溯机制允许递归函数在栈中不断推入和弹出帧,以执行递归操作。
Q:意思是说,递归实现中序遍历的算法,是从根节点开始依次遍历它的左节点,并在每一次遍历的时候都把遍历到的节点压入栈中?
不完全正确。递归中序遍历算法并不使用栈来显式地压入遍历的节点,而是利用函数调用栈的特性来完成中序遍历的过程。在递归中序遍历中,递归函数会依次遍历树的左子树,然后访问当前节点,最后遍历右子树。这一过程是通过递归函数的不断调用实现的,不需要额外的栈数据结构。
让我详细解释一下递归中序遍历算法的执行过程:
-
递归函数
inorderHelper(node, result)从根节点开始调用,node是当前节点,result是存储遍历结果的列表。 -
当函数调用到
inorderHelper(node.left, result)时,它会递归地遍历左子树,将左子树的节点压入函数调用栈。 -
当函数返回到当前节点,它会执行
result.append(node.val)将当前节点的值添加到结果列表。 -
然后,函数调用
inorderHelper(node.right, result),递归地遍历右子树,将右子树的节点压入函数调用栈。 -
这个过程会一直重复,直到遍历完整棵树的左子树,然后是根节点,最后是右子树。
-
当递归函数的执行结束时,控制会自动返回到上一个函数调用,实现回溯。因此,在递归中,遍历的节点不是显式地压入栈,而是通过递归函数的调用和回溯来实现的。
这种递归中序遍历的过程可以看作是在使用函数调用栈来维护遍历的状态,而不需要额外的栈数据结构。这使得中序遍历的实现相对简单,因为栈的操作是隐式的。
Q:函数调用栈跟栈有什么区别吗?
函数调用栈(或简称调用栈)和栈是两个不同的概念,虽然它们都涉及到"栈"这个词,但它们有不同的用途和工作原理。
-
函数调用栈(调用栈):
- 函数调用栈是一种数据结构,用于跟踪程序的函数调用和返回顺序。
- 它是在程序运行时自动管理的,用于存储函数的局部变量、函数参数、返回地址等信息。
- 函数调用栈遵循先进后出(Last In, First Out,LIFO)的原则,即最后调用的函数最先返回。
- 在递归中,函数的调用和返回操作会在调用栈中不断推入和弹出帧。
-
栈:
- 栈是一种抽象数据类型,用于存储和管理数据元素。
- 它可以在任何编程语言中手动实现,通常用于实现后进先出(Last In, First Out,LIFO)的数据结构。
- 栈可以用于许多目的,包括在数据结构和算法中实现操作,如中缀表达式转后缀表达式、深度优先搜索(DFS)、递归算法等。
虽然两者都涉及栈的概念,但它们的用途和工作方式不同。函数调用栈是编程语言的一部分,用于管理函数调用和返回。栈是一种通用的数据结构,可以手动实现,并用于各种编程任务。在递归等情况下,函数调用栈通常与栈数据结构一起使用,以实现递归函数的调用和回溯。
相关文章:

【chatgpt问答记录】双端队列、栈和函数调用栈
collections.deque和queue.Queue的区别 Q:collections.deque()跟queue.Queue()有什么区别? collections.deque() 和 queue.Queue 是两种不同的数据结构,它们有一些区别: 实现方式: collections.deque() 是 Python 标…...
另辟蹊径者 PoseiSwap:背靠潜力叙事,构建 DeFi 理想国
前不久,灰度在与 SEC 就关于 ETF 受理的诉讼案件中,以灰度胜诉告终。灰度的胜利,也被加密行业看做是加密 ETF 在北美地区阶段性的胜利, 该事件也带动了加密市场的新一轮复苏。 此前,Nason Smart Money 曾对加密市场在 …...
如何查看笔记本电脑电池损耗
1.下载图吧工具箱 在官网下,不要下错了,不然会有很多垃圾捆绑软件,我放一个百度云链接,安装包上传上去了 链接:https://pan.baidu.com/s/18dguF5OGktbPkW7EszZZqA 提取码:1024 2.安装打开后点击主办工具-…...
一键批量视频剪辑、合并,省时省力,制作专业视频
在当今数字化的时代,视频制作的需求日益增长。无论是个人用户还是专业人士,都需要能够快速、高效地处理视频,以适应不同的需求。但是,视频剪辑和合并往往是一个耗时且需要专业技能的过程。有没有一种方法可以简化这个过程…...

使用R语言构建HTTP爬虫:IP管理与策略
目录 摘要 一、HTTP爬虫与IP管理概述 二、使用R语言进行IP管理 三、爬虫的伦理与合规性 四、注意事项 结论 摘要 本文深入探讨了使用R语言构建HTTP爬虫时如何有效管理IP地址。由于网络爬虫高频、大量的请求可能导致IP被封禁,因此合理的IP管理策略显得尤为重要…...
Stable Diffusion源码调试(二)
Stable Diffusion源码调试(二) 个人模型主页:https://liblib.ai/userpage/369b11c9952245e28ea8d107ed9c2746/model Stable Diffusion版本:https://github.com/AUTOMATIC1111/stable-diffusion-webui/releases/tag/v1.4.1 分析S…...

网络安全(黑客)-零基础自学
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全…...

在线CRM系统的安全性高吗?企业该如何选择?
在线CRM系统具备门槛低、功能不打折扣、部署周期短等优点,相比本地化部署更加适合中小企业。但很多企业在选型软件时会顾虑在线CRM系统的安全性高吗? 通常情况下厂商会比中小企业更有实力保证数据安全,从技术手段保护企业隐私不被盗用。 数…...

R-install_miniconda()卸载 | conda命令行报错及解决方法
运行以下代码,突然报错: C:\Users\hp>conda info-e >>>>>>>>>>>>>>>>>>>>>> ERROR REPORT <<<<<<<<<<<<<<<<<<<<&…...

leaflet:利用Leaflet-Geoman绘制多种图形,导出为geojson文件(135)
第135个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中利用Leaflet-Geoman绘制多种图形,导出为geojson文件。 灵活地配置Leaflet-Geoman的属性,可以产生各种美妙的绘图效果。利用FileSaver可以导出geojson文件。 直接复制下面的 vue+leaflet源代码,操作2分钟…...

【C语言基础】第02章_变量与进制
讲师:康师傅 视频:https://www.bilibili.com/video/BV1Bh4y1q7Nt?p1&vd_source3eaa9d17f2454e1ae80abc50d16e66b5 文章目录 本章专题脉络1关键字(keyword)2标识符(Identifier)3变量(variable)3.1 为什么需要变量3.2 初识变量3.3 变量的声明与赋值步…...

【案例教程】基于AERMOD模型在大气环境影响评价中的实践技术应用
大气污染是工农业生产、生活、交通、城市化等方面人为活动的综合结果,同时气象因素是控制大气污染的关键自然因素。大气污染问题既是局部、当地的,也是区域的,甚至是全球的。本地的污染物排放除了对当地造成严重影响外,同时还会在…...

【C语言从入门到放弃 4】字符串,结构体,共用体,位域,typedef详解
C语言是一种广泛应用于系统编程和嵌入式开发的高效编程语言。在本文中,我们将介绍C语言中的一些重要概念,包括字符串、结构体、共用体、位域和typedef,并提供简单的示例代码。 字符串 在C语言中,字符串是以空字符(\0…...

Linux学习第34天:Linux LCD 驱动实验(一):星星之火可以燎原
Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 LCD显示屏是由一个一个的像素点构成的。当你能控制一个像素点的亮暗及颜色变化的时候,你就能让LCD显示瓶显示五颜六色的整幅图案。甚至可以让LCD屏幕…...

Flink SQL Window TopN 详解
Window TopN 定义(⽀持 Streaming): Window TopN 是特殊的 TopN,返回结果是每⼀个窗⼝内的 N 个最⼩值或者最⼤值。 应⽤场景: TopN 会出现中间结果,出现回撤数据,Window TopN 不会出现回撤数据…...

leetcode做题笔记216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件: 只使用数字1到9每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。 示例 1: 输入: k 3, n 7 输出: [[1,2,4]] 解释…...
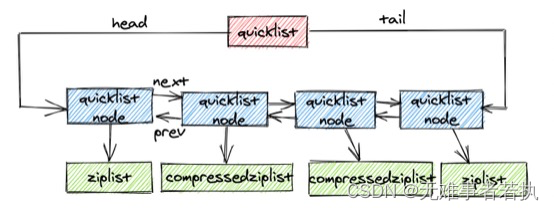
Redis系列-Redis数据类型【3】
目录 Redis系列-Redis数据类型【3】字符串类型(String)SDS (simple dynamic string) 哈希类型(Hash)列表类型(List)集合类型(Set)有序集合类型(ZSet)字符串类…...
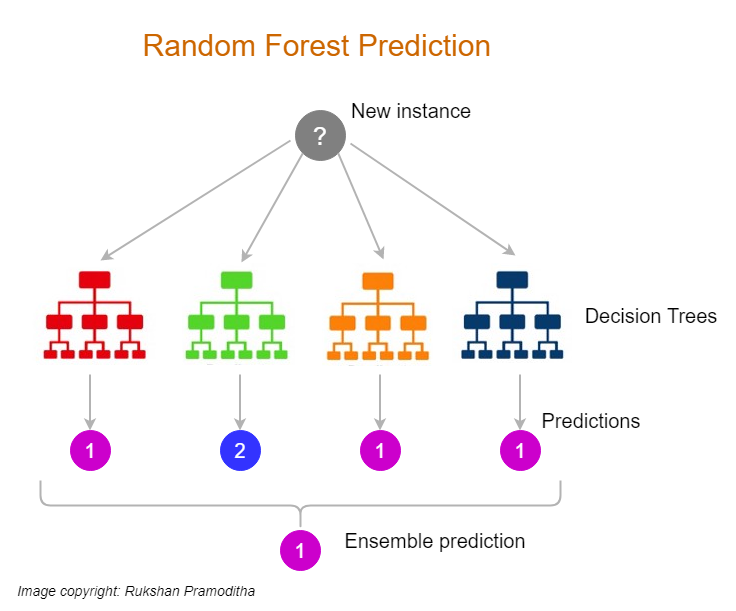
机器学习 - 决策树:技术全解与案例实战
目录 一、引言二、决策树基础决策树模型概述构建决策树的关键概念特征选择决策树的生成 决策树的剪枝 三、算法研究进阶提升树和随机森林提升树(Boosted Trees)随机森林(Random Forests) 进化算法与决策树决策树结构的进化 多目标…...

Opus 1.4 编译脚本
Opus 1.4 编译脚本 官网地址:https://www.opus-codec.org/ 仓库地址:https://gitlab.xiph.org/xiph/opus #!/bin/bash# 每次编译删除原来的编译文件 rm build -rf rm install -rf # 创建临时编译目录,避免污染源文件 mkdir build # 定义一…...
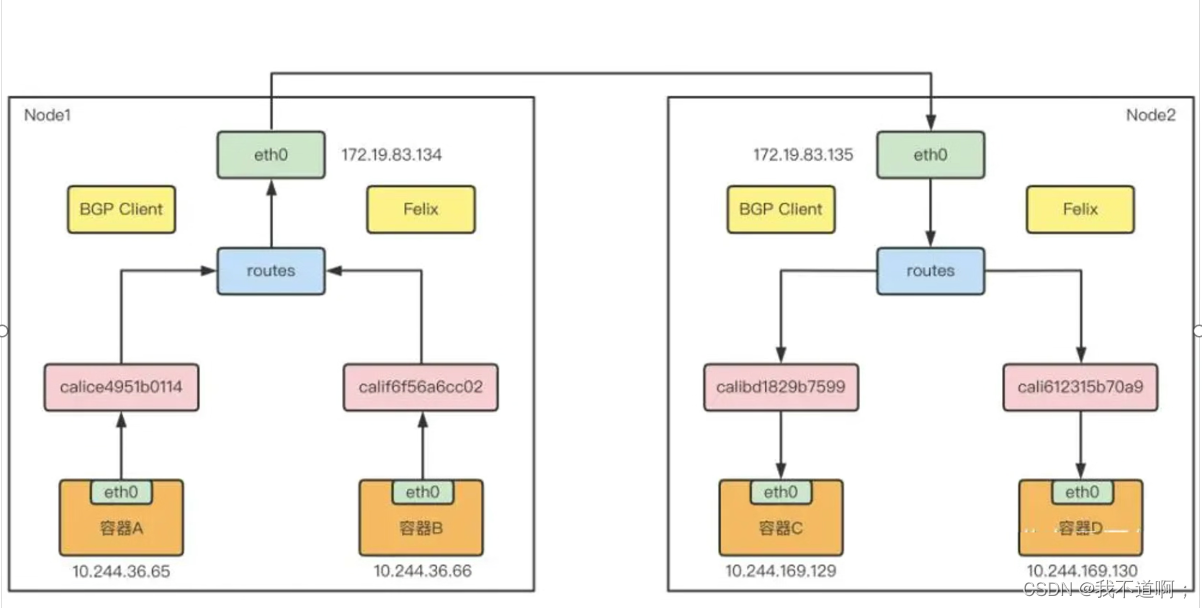
二进制搭建及高可用 Kubernetes v1.20
目录 一、实验规划: 二、操作系统初始化配置: 1. 关闭防火墙 selinux: 2. 关闭swap分区: 3. 根据规划设置主机名: 4. 所有主机添加hosts: 5. 调整内核参数: 6. 时间同步: 三、部署 etcd 集群:…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
