基于袋獾算法的无人机航迹规划-附代码
基于袋獾算法的无人机航迹规划
文章目录
- 基于袋獾算法的无人机航迹规划
- 1.袋獾搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用袋獾算法来优化无人机航迹规划。
1.袋獾搜索算法
袋獾算法原理请参考:https://blog.csdn.net/u011835903/article/details/130543093
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得袋獾搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用袋獾算法对航迹评价函数式(7)进行优化。优化结果如下:


从结果来看,袋獾算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于袋獾算法的无人机航迹规划-附代码
基于袋獾算法的无人机航迹规划 文章目录 基于袋獾算法的无人机航迹规划1.袋獾搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用袋獾算法来优化无人机航迹规划。 1.袋獾搜索算法 …...

2024上海智博会,上海国际智慧城市,物联网,大数据展会(世亚智博会)
中国国际智慧城市,物联网,大数据博览会(简称:世亚智博会)自2010年创办以来,至今已成功举办十多届。世亚智博会是中国较高、规模较大、影响力较广的展会;是被国际业界公认的不可错过的名展之一。随着世亚智博会的国际地位和影响不断…...

家庭教育质量提升成未来教育关注重点
随着教育改革的不断深化,家校合作模式也在实践中不断探索和丰富。 11 月 6 日,第六届长三角家校合作论坛于上海杨浦盛大开幕,此次论坛围绕“家校协同与人的学校领导”这一主题展开深度研讨。论坛旨在交流和分享相关经验及做法,以…...

python入门系列(1)—— 环境安装
前言 社区里面有好多同学想要入门python,可能源于以下原因: 易学性:Python 的语法简洁、清晰,容易理解和上手,使得初学者能够轻松入门编程。无论是编写基本的脚本还是进行更复杂的开发,Python 都提供了友…...

react组件通信
目录 前言: 父子组件通信 子父组件通信 兄弟组件通信 总结 前言: React是一种流行的JavaScript库,用于构建现代化的、高性能的Web应用程序。在React中,组件是代码的构建块。组件通信是React中一个非常重要的概念,…...

学习笔记|Pearson皮尔逊相关系数|Spearman斯皮尔曼相关系数|和Kendall肯德尔tau-b相关系数|分析流程|-SPSS中双变量相关性分析系数
目录 学习目的软件版本原始文档基础概念皮尔逊相关系数基本假设(适用条件):系数的范围及意义实例1. 读数据:2.正态性检验:3.异常值检验(体重):4.分析: 斯皮尔曼相关系数基…...

计算机服务器中了locked勒索病毒怎么办,勒索病毒解密,数据恢复
随着网络技术的不断成熟,网络中存在的病毒威胁也不断增多,近期,云天数据恢复中心陆续接到很多企业的求助,企业的计算机服务器数据库遭到了勒索病毒攻击,并且勒索病毒的攻击与加密形式也发生了许多变化。其中攻击次数较…...

本地生活餐饮视频怎么拍摄能有更多流量?如何批量生产呢?
本地生活近几年特别的火,所以到现在各类内容雷同性也比较高,视频缺少新的创意和玩法,像餐饮店的视频,大部分都是拍顾客进门、拍餐饮店座无虚席的实景……作为用户,其实早就已经看腻了。 今天推荐本地生活餐饮店商家拍…...
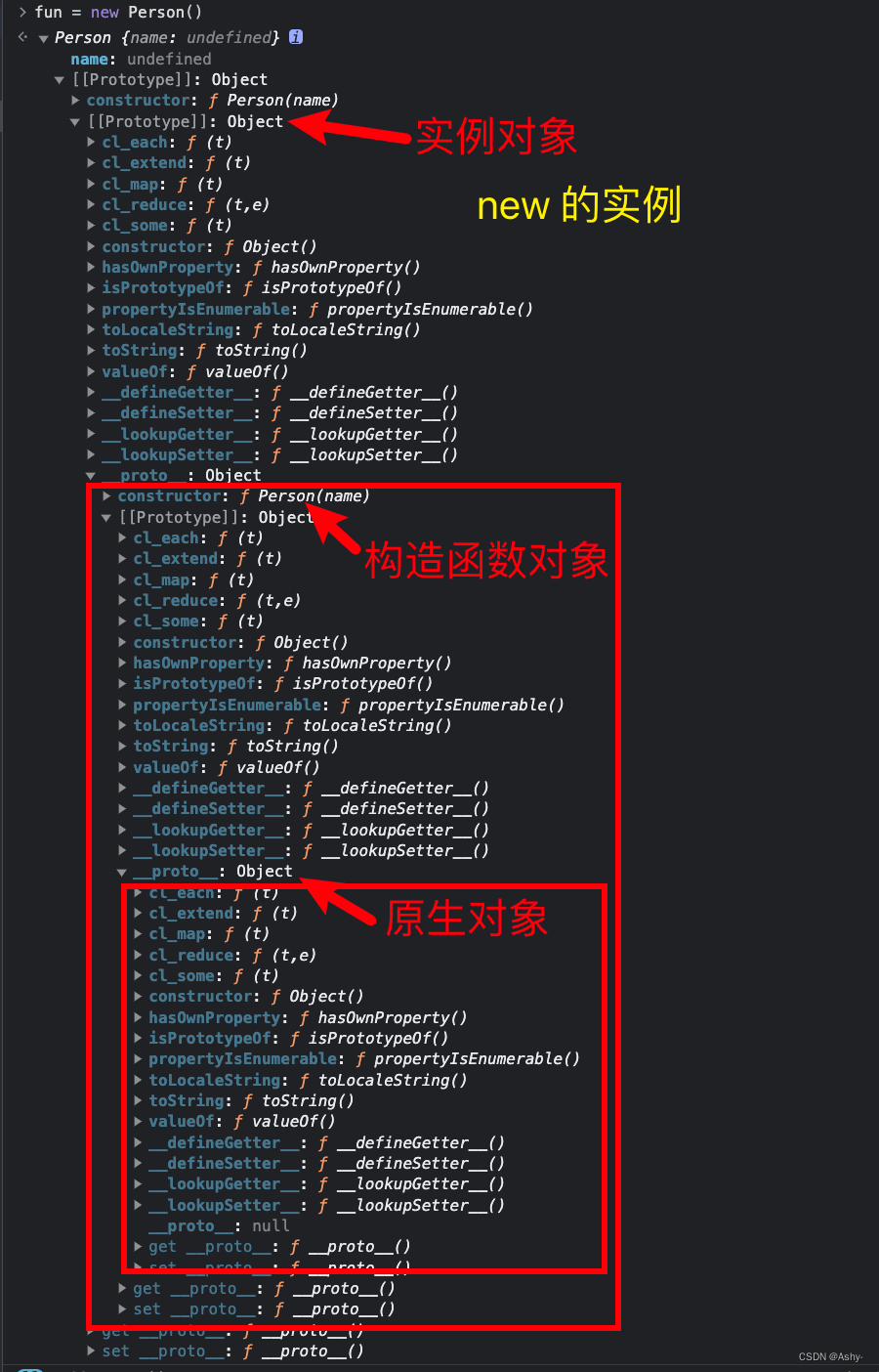
【笔记】原型和原型链(持续完善)
概念 原型:函数都具有 prototype 属性,称之为原型,也称之为原型对象 1.1 原型可以放一些属性和方法,共享给实例对象使用(也就是原生方法)。 1.2 原型可以做继承原型链:对象都有 __proto__ 属性…...

python向word中添加表格
1、表格插入 方法一:直接创建表添加 #导入库 from docx import Document #创建文档对象 document Document()#创建5行7列表格 table document.add_table(rows5, cols7)#修改第2行第3列单元格的内容为中国 table.cell(1,2).text中国 #修改第3行第4列单元格的内容…...
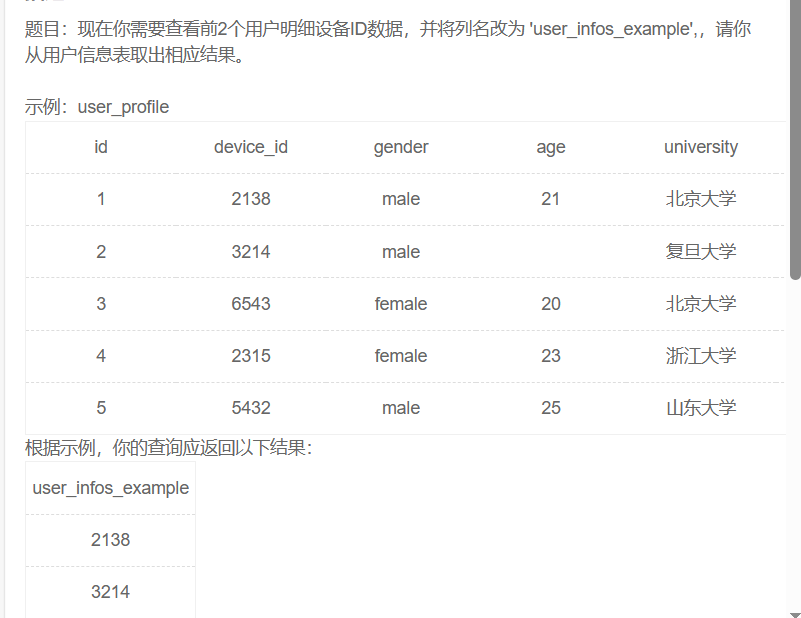
2023_11_6 每日半小时 SQL 刷题
文章目录 1. 查询所有列题目描述SQL 语句编写 2. 查询多列题目描述SQL 语句编写 3. 查询结果去重题目描述SQL 语句编写 4. 查询结果限制返回行数题目描述SQL 语句编写 5. 将查询后的列重新命名题目描述SQL 语句编写 语法小总结 1. 查询所有列 题目链接:SQL1 查询所…...
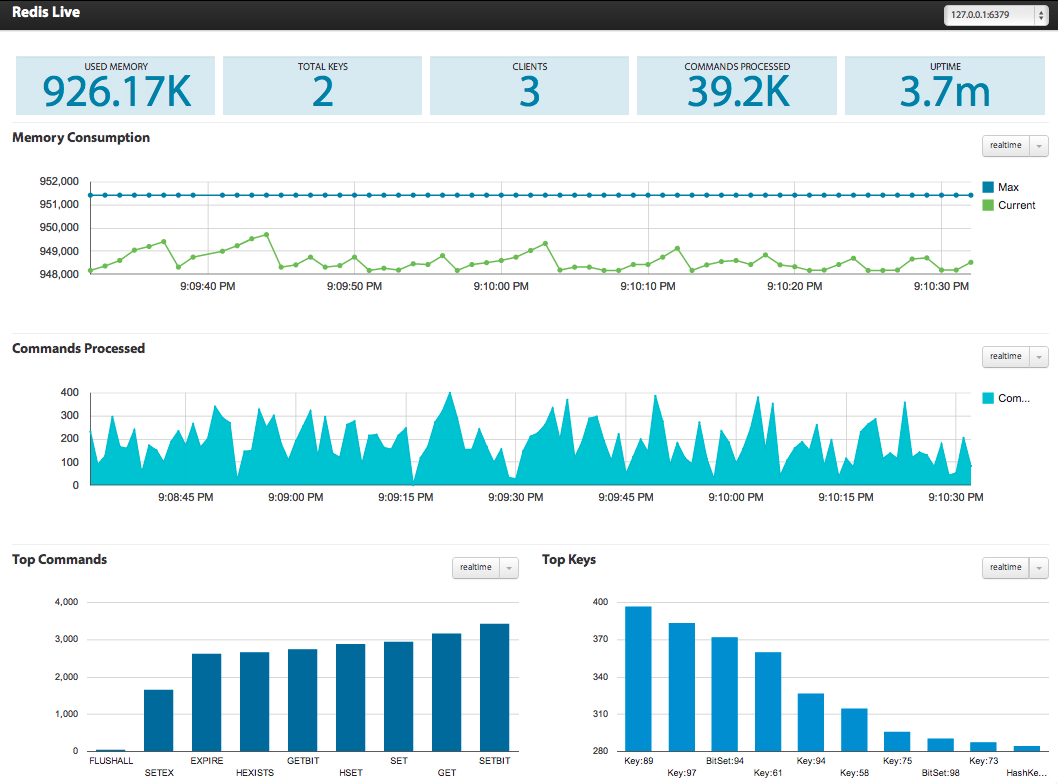
Redis系列-Redis性能优化与安全【9】
目录 Redis系列-Redis性能优化与安全【9】Redis性能优化策略Redis安全设置与防护措施Redis监控与诊断工具介绍 七、Redis应用案例与实战八、Redis未来发展与趋势 个人主页: 【⭐️个人主页】 需要您的【💖 点赞关注】支持 💯 Redis系列-Redis性能优化与安…...
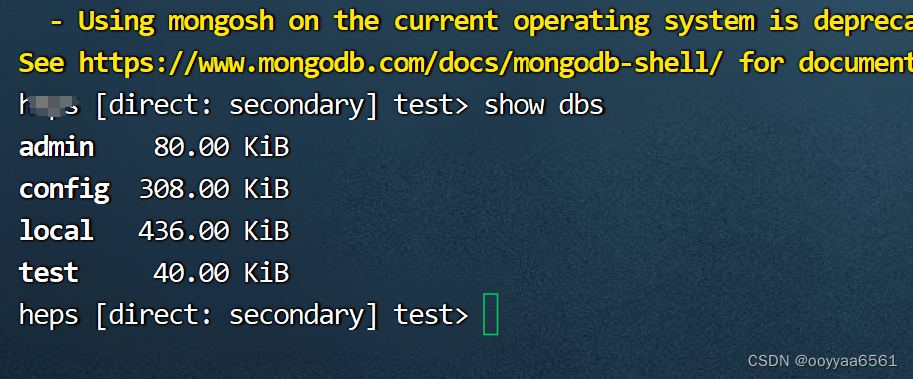
centos7下安装主从仲裁三台结构的MongoDB 7.0.4
安装手册英文版在这里 https://www.mongodb.com/docs/v7.0/tutorial/install-mongodb-on-red-hat/ 我的安装过程 1)基础安装 1、创建 /etc/yum.repos.d/mongodb-org-7.0.repo文件 下面的代码复制到这个文件中,保存 [mongodb-org-7.0] nameMongoDB Re…...

2258. 逃离火灾 : 详解如何从「二分」到「分类讨论」(图解过程)
题目描述 这是 LeetCode 上的 「2258. 逃离火灾」 ,难度为 「困难」。 Tag : 「多源 BFS」、「二分」、「预处理」 给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid,它表示一个网格图。 每个格子为下面 个值之一: 0 表示草地。 1 表…...

基于SSM框架的共享单车管理系统小程序系统的设计和实现
基于SSM框架的共享单车管理系统小程序系统的设计和实现 源码传送入口前言主要技术系统设计功能截图Lun文目录订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码传送入口 前言 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,…...
COOHOM通过采用亚马逊云科“专库专用”的方式,为云原生的构建提供稳定的数据支撑
全球化浪潮下,面对全球化业务发展带来的新需求与新挑战,越来越多的企业开启了云原生构建旅程,以推动业务系统快速迭代,为国际业务的拓展打下坚实的基础。COOHOM是杭州群核信息技术有限公司旗下的国际化品牌。为全球企业和个人提供…...
Java根据一个List内Object的两个字段去重
背景 在Java开发过程中,我们经常会遇到需要对List进行去重的需求。 其中常见的情况是,将数组去重,或者将对象依据某个字段去重。这两种方式均可用set属性进行处理。 今天讨论,有一个List,且其中的元素是自定义的对象&…...

运维那些事儿|2023年,运维还有出路吗?
作为一名运维,不知道你有没有这样的感受。 觉得自己的工作没什么成长空间。每天装个系统、跑个机房、跑个脚本,忙来忙去也没忙出来什么名堂,含金量低不说,薪资也一直没见涨,所以你开始陷入迷茫,会疑惑&…...
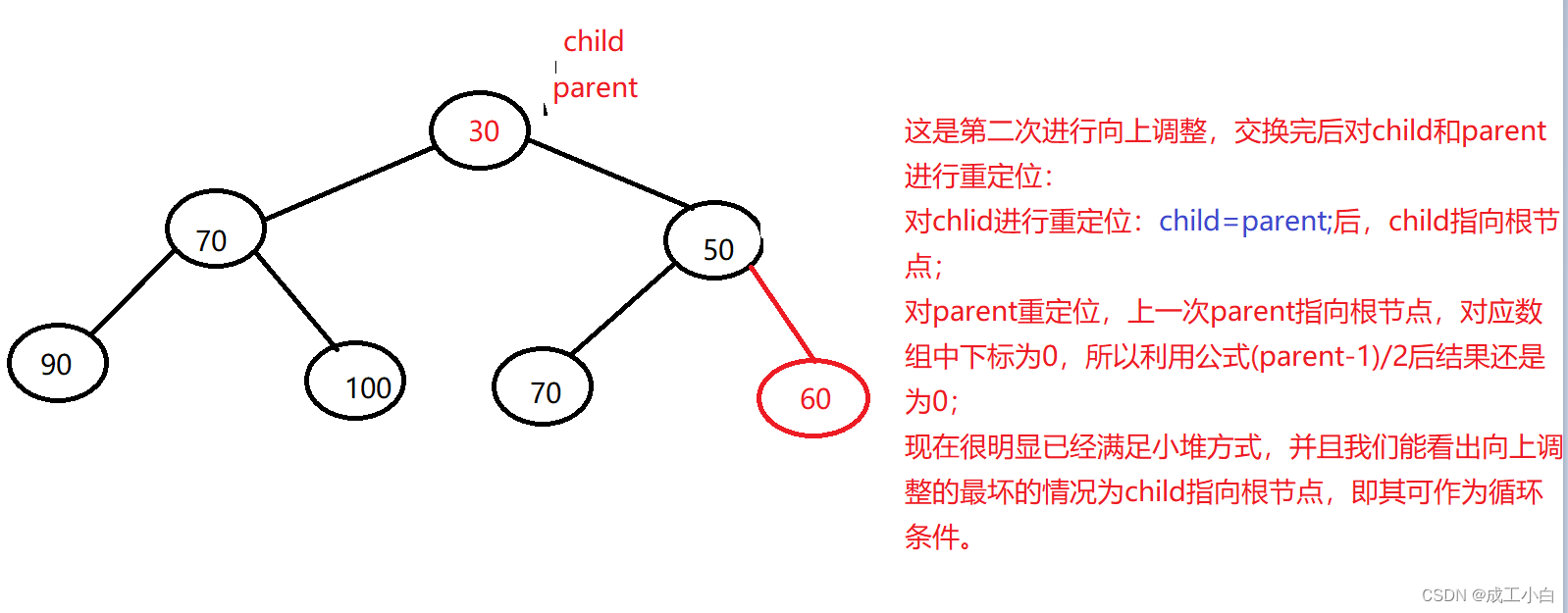
数据结构——二叉树(2)
接上一篇文章http://t.csdnimg.cn/nsKsW,本次我们接着讲解关于二叉树的相关知识。 一、二叉树的相关性质: 1. 若规定根节点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有 2^(i-1) 个结点. 2. 若规定根节点的层数为 1 ,则 深度…...
aosp定制android系统
目录 AOSP 准备工作(配置) 确定机型和版本 初始化 git安装 curl安装 同步源码 环境变量 创建aosp目录 指定同步版本 解下来安装编译需要的依赖 编译aosp源码 刷入系统 AOSP 全称 Android Open Source Project 是指Android开源项目,它是由Google主导的…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
