后入能先出,一文搞懂栈
目录
- 什么是栈
- 数组实现
- 链表实现
- 栈能这么玩
- 总结
什么是栈
栈在我们日常编码中遇到的非常多,很多人对栈的接触可能仅仅局限在 递归使用的栈 和 StackOverflowException,栈是一种后进先出的数据结构(可以想象生化金字塔的牢房和生化角斗场的狗洞)。
栈(stack)是一种运算受限的线性数据结构,它具有以下特点:
1. 运算受限: 栈限定仅在表尾进行插入和删除操作,这一端被称为栈顶,而另一端称为栈底。这限制了对栈的操作,只能按照后进先出(LIFO,Last-In-First-Out)的原则进行插入和删除操作。插入操作又称为进栈、入栈或压栈,它将新元素放到栈顶,使之成为新的栈顶元素;删除操作又称为出栈或退栈,它将栈顶元素删除,使其相邻的元素成为新的栈顶元素。
2. 线性表: 栈也是一种线性表,它表示数据元素之间的逻辑关系是线性的。虽然具体实现可以使用数组或链表等不同的物理存储结构,但逻辑上各个元素之间是相邻的,操作也是按照顺序进行的。
3. 栈顶和栈底: 栈的逻辑结构中有栈顶和栈底的概念。栈顶表示可以进行插入和删除操作的一端,通常与数组的末尾或链表的头部有关。栈底则是相对的另一端,用于限制操作的另一端。
4. 栈的应用: 栈在计算机科学和编程中有广泛的应用,例如程序执行调用堆栈、四则运算表达式求值、非递归算法实现、括号匹配问题、浏览器历史、内存分配、任务管理等的解决。掌握栈是非常重要的,它是必须了解的数据结构之一。
栈可以使用数组或链表来实现,选择合适的实现方式取决于具体的应用场景和性能需求。数组实现的栈通常更适合于需要固定大小的栈(当然也可以进行扩容),而链表实现的栈可以动态扩展,适用于不确定大小的栈。在栈的操作中,栈顶元素是非常关键的,因为它在插入和删除操作中起着重要作用。
总之,栈是一个非常有用的数据结构,它在计算机科学中扮演着重要的角色,了解它的特性和应用对于编程和算法设计至关重要。
对于一个栈的接口,我们简易定义如下:
public interface Stack<T> {void push(T item); // 压栈T pop(); // 弹栈T peek(); // 获取栈顶元素boolean isEmpty(); // 判断栈是否为空int size(); // 返回栈的大小
}
数组实现
数组实现的栈用的比较多,我们经常刷题也会用数组去实现一个简单的栈去解决简单的问题。
结构设计
对于数组来说,我们模拟栈的过程很简单,因为栈是后进先出,我们很容易在数组的末尾进行插入和删除。所以我们选定末尾为栈顶。所以对于一个栈所需要的基础元素是 一个array[]数组和一个size表示大小,还需要一个负载因子表示数组的大小。
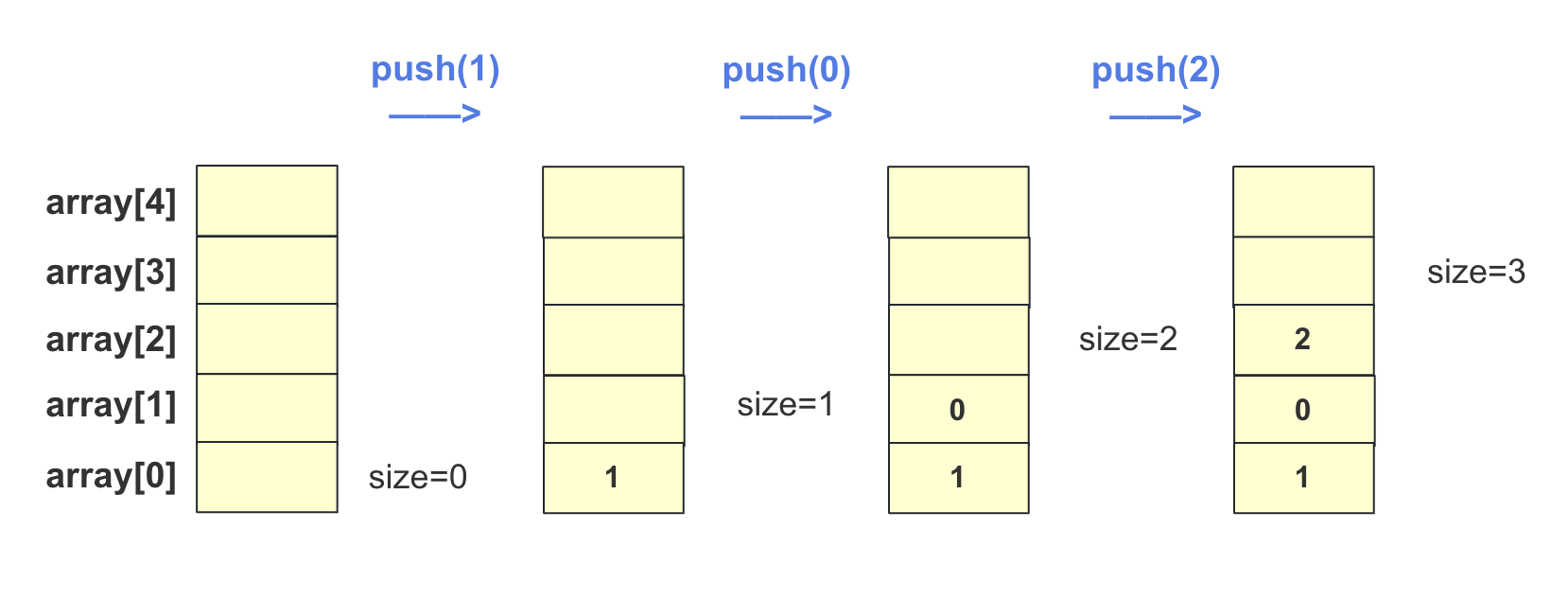
push入栈操作
- 如果数组满了,需要扩容
- size位置赋值,
array[size++] = data;
pop弹出栈并返回首位
- 如果栈不为空,可以弹出。
return array[--size];
如下图,当栈中还剩1,2,3,4执行pop操作,栈顶变为3的位置并且返回4
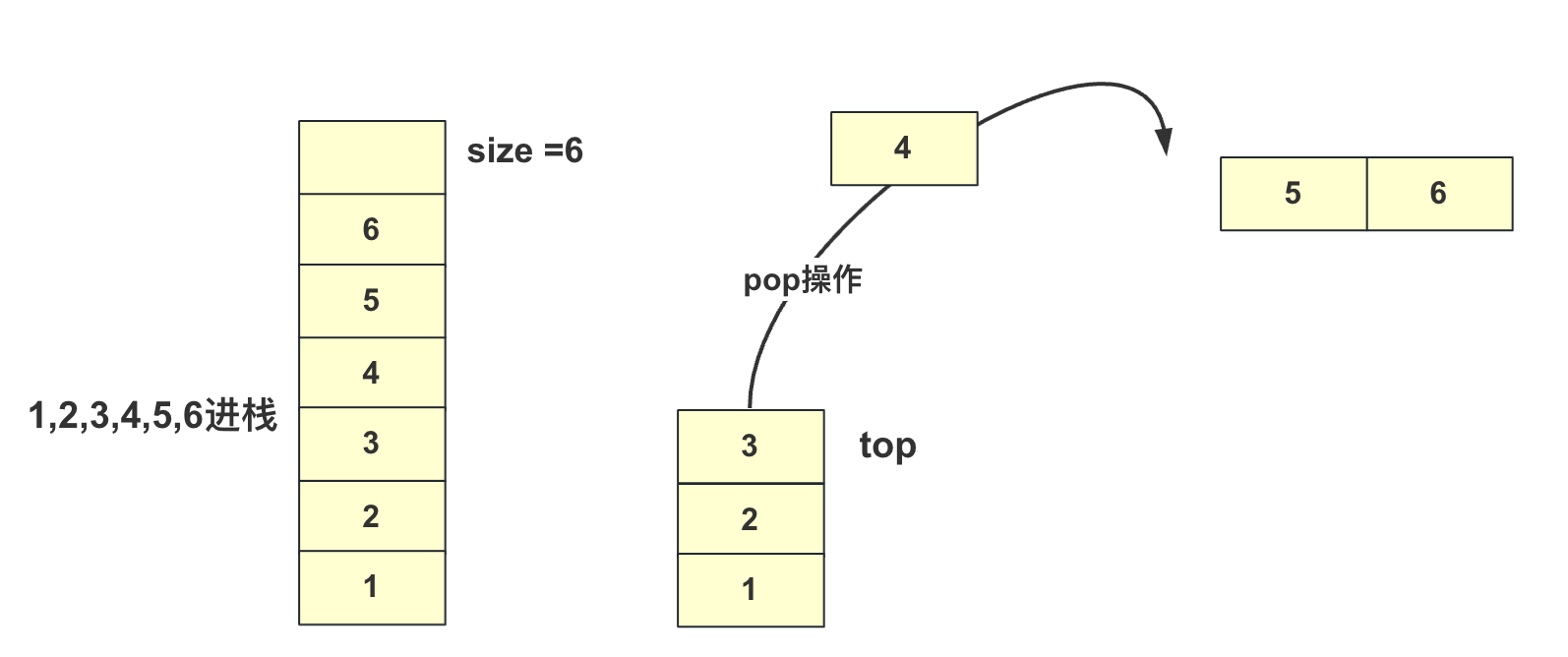
peek返回栈顶
- peek操作时返回栈顶不弹出,所以栈不为空时候
return data[size-1]即可。
数组实现:
import java.util.EmptyStackException;public class SeqStack<T> implements Stack<T> {private T array[];private int size;private static final int DEFAULT_CAPACITY = 10;public SeqStack() {this.size = 0;array = (T[]) new Object[DEFAULT_CAPACITY];}@Overridepublic void push(T data) {if (size == array.length) {// 如果数组已满,扩展数组resizeArray();}array[size++] = data;}@Overridepublic T pop() {if (isEmpty()) {throw new EmptyStackException();}// 下面可以写成 return array[--size];T data = array[size - 1];size--;return data;}@Overridepublic T peek() {if (isEmpty()) {throw new EmptyStackException();}return array[size - 1];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic int size() {return size;}private void resizeArray() {int newCapacity = (int) (array.length * 2);T[] newArray = (T[]) new Object[newCapacity];for (int i = 0; i < size; i++) {newArray[i] = array[i];}array = newArray;}
}
链表实现
栈可以使用数组或链表来实现,两种思路如下:
- 链表尾部作为栈顶: 在数组实现中,栈的操作是在尾部进行插入和删除。链表中即使使用尾指针可以提高尾部插入效率,但删除操作仍然需要查找前驱节点。要实现高效的删除操作,需要使用双向链表,这增加了整个结构的复杂性。
- 链表头部作为栈顶: 在这种实现中,栈的设计不带头节点的单链表(不需要哑结点),所有操作都在链表的头部进行。头部插入删除都很方便效率比较高,编写代码也很简单。
基础结构
public class LinkedStack<T> implements Stack<T> {private Node<T> top;private int size;public LinkedStack() {top = null;size = 0;}private static class Node<T> {T data;Node<T> next;public Node(T data) {this.data = data;this.next = null;}}//其他方法
}
push入栈
与不带头结点单链表头插入一致
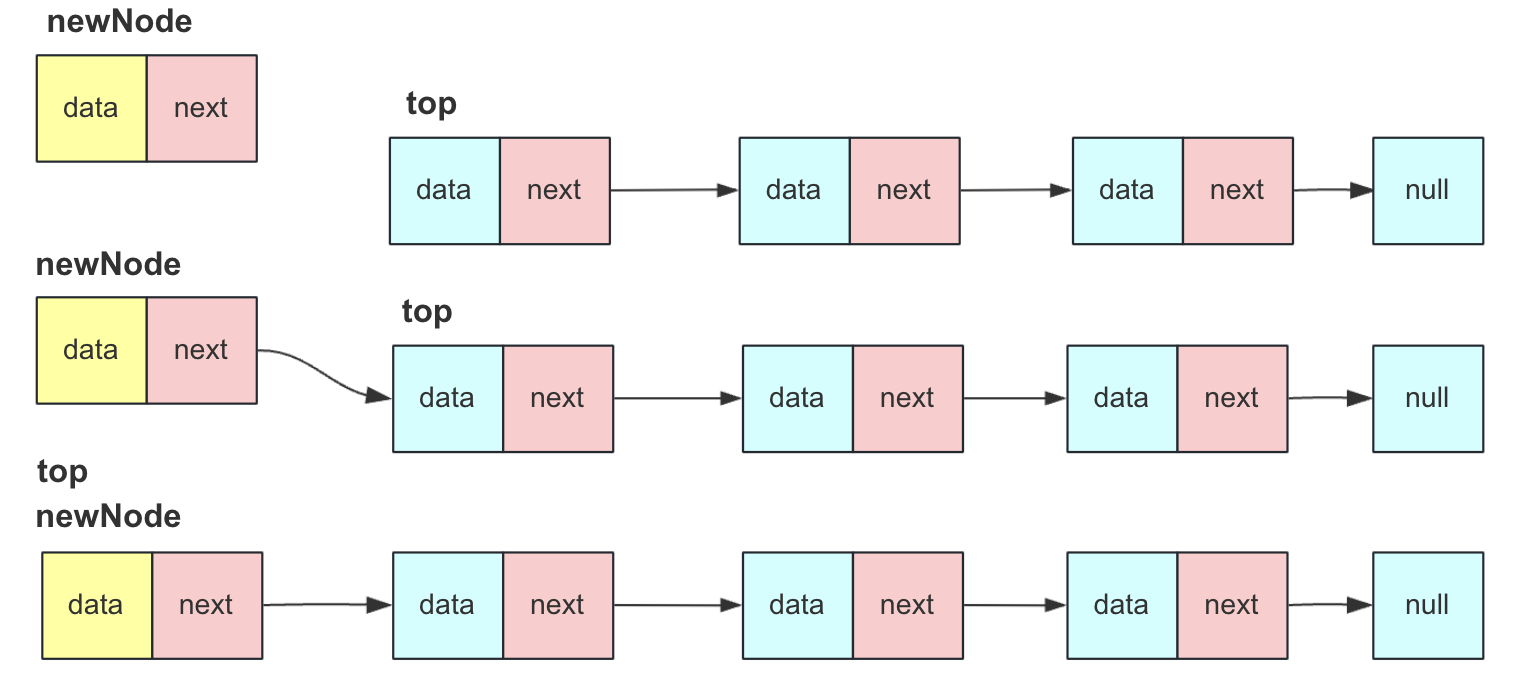
- 创建新节点
- 新节点的next指向栈顶节点top
- 栈顶节点top指向新节点,表示这个节点为新的栈顶节点
- size++
部分操作流程如下图
pop弹出
与不带头结点单链表头插入一致
- 判断是否为空
- 记录头结点top的值data
- 头结点top指向top.next
- size–,返回前面记录的值data
部分操作流程如下图
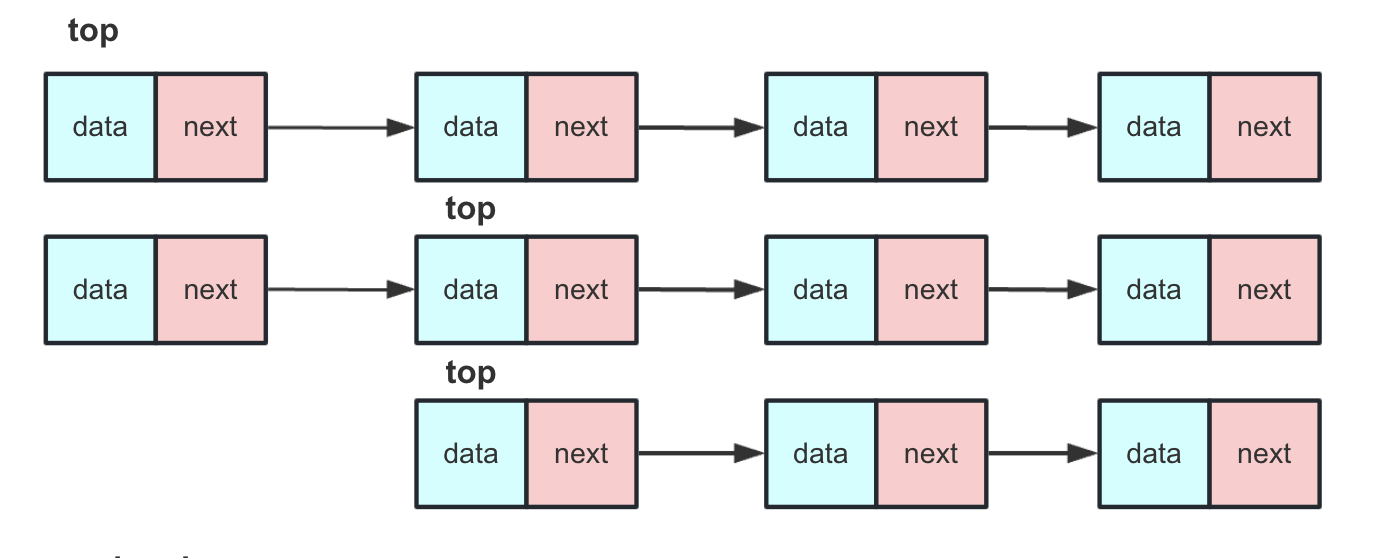
peek返回栈顶
不为空的时候返回 top.data即可
链表实现:
import java.util.EmptyStackException;public class LinkedStack<T> implements Stack<T> {private Node<T> top;private int size;public LinkedStack() {top = null;size = 0;}private static class Node<T> {T data;Node<T> next;public Node(T data) {this.data = data;this.next = null;}}@Overridepublic void push(T item) {Node<T> newNode = new Node<>(item);newNode.next = top;top = newNode;size++;}@Overridepublic T pop() {if (isEmpty()) {throw new EmptyStackException();}T data = top.data;top = top.next;size--;return data;}@Overridepublic T peek() {if (isEmpty()) {throw new EmptyStackException();}return top.data;}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic int size() {return size;}
}
栈能这么玩
既然上面详细讲解设计栈,这里来两道栈非常经典非常经典的例题(非常高频,很容易忘,又很重要,普通问题就不放的)
力扣20有效的括号:
题意:给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 :
输入:
"()[]{}"
输出: true
示例 :
输入:
"([)]"
输出: false
分析:
括号类的问题是经典栈类问题,肯定要想到用栈处理。判断一个字符串满不满足一个有效的字符串,就要看它是不是都能组成对。
从单个括号对来说,((,))都是不满足的,只有()才可满足,即一左一右。
从多个括号对来说 {[(字符串还可接受任意无限(,[,{的括号。但是如果向左的括号只能先接收)括号(变成{[)。
从上面可以看作一种相消除的思想。例如(({[()()]}))字符串遍历时候可以这样处理:
(({[(下一个)消掉成(({[(({[(下一个)消掉成(({[(({[下一个]消掉成(({(({下一个}消掉成((((下一个)消掉成((下一个)消掉成
每次操作的时候都判断剩余有效括号最顶部那个括号是否能够和遍历的相消除,这个过程利用栈判断当前是加入栈还是消除顶部,到最后如果栈为空说明满足,否则不满足,当然具体括号要对应,具体实现代码为:
public boolean isValid(String s) {Stack<Character> stack = new LinkedStack<Character>();for (int i = 0; i < s.length(); i++) {char te = s.charAt(i);if (te == ']') {if (!stack.isEmpty() && stack.pop() == '[')continue;else {return false;}} else if (te == '}') {if (!stack.isEmpty() && stack.pop() == '{')continue;else {return false;}} else if (te == ')') {if (!stack.isEmpty() && stack.pop() == '(') {continue;} else {return false;}} else {stack.push(te);}}return stack.isEmpty();
}
当然,JDK自带的栈用起来不快,可以用数组优化:
public boolean isValid(String s) {char a[] = new char[s.length()];int index = -1;for (int i = 0; i < s.length(); i++) {char te = s.charAt(i);if (te == ']') {if (index >= 0 && a[index] == '[')index--;else {return false;}} else if (te == '}') {if (index >= 0 && a[index] == '{')index--;else {return false;}} else if (te == ')') {if (index >= 0 && a[index] == '(')index--;else {return false;}} else {a[++index] = te;}}return index == -1;
}
力扣32最长有效括号(困难)
题目描述:给定一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长的包含有效括号的子串的长度。
示例 :
输入: “(()”
输出: 2
解释: 最长有效括号子串为 “()”
示例 :
输入: “)()())”
输出: 4
解释: 最长有效括号子串为 “()()”
方案一暴力
这种题核心思想就是使用栈模拟。本题的话更简单一点因为只有(和)两种括号,使用暴力的时候就可以循环每次找到最长的有效括号。而括号匹配的时候可以直接终止的情况是)右括号多出无法匹配。
例如())(到第三个不可能和前面相连。如果来(只需要期待后面能够来),一个)可以和一个(组成一对,消除栈中的一个(。
当然,在具体的实现上,我们用数组模拟栈,实现代码为:
public int longestValidParentheses(String s) {char str[] = s.toCharArray();//字符数组int max = 0;for (int i = 0; i < str.length - 1; i++) {int index = -1;if (max >= str.length - i)break;for (int j = i; j < str.length; j++) {if (str[j] == '(') {index++;} else {if (index < 0) {i = j;break;} else {index--;}}if (index == -1 && (j - i + 1 > max)) {max = j - i + 1;}}}return max;
}
这个复杂度太高,我们看看如何用栈优化。
方案二栈优化
如何将这道题从一个O(n^2)的时间复杂度优化到O(n)?这其实非常简单,只需要注意处理的过程。让我们首先考虑一些可能的最大情况。
( ) )( ) ( ( ) ( ) )最大为后面部分(空格分开)( ) ( )( ( ( )最大为前面部分( ( ( ( (( ) ( ) ( ) ( )最大为后面部分
在处理这道题时,我们会注意到不同类型的括号可能会有一些区别:
(:左括号一旦出现那么他就期待一个)进行匹配,但它的后面可能有)并且在这中间有很多其他括号对。
):右扩号有两种情况:
- 一种是当前已经超过左括号前面已经不可能连续了。例如
( ) ) ( )第三个括号出现已经使得整个串串不可能连续,最大要么在其左面,要么再其右面。 你可以理解其为一种清零初始机制。 - 另一种情况
)就是目标栈中存在(可与其进行匹配。匹配之后要叠加到消除后平级的数量上,并且判断是否是最大值。(下面会解释)
在具体实现的思路上,就是使用一个int数组标记当前层级(栈深)有正确的括号数量。 模拟一次栈行为从左向右,遇到)太多(当前栈中不存在(进行匹配)就将数据清零重新开始。这样一直到最后。你可以把它看成台接,遇到(就上一个台阶并清零该新台阶,遇到)就下一个台阶并且把数量加到下降后的台阶上。具体可以看下面图片模拟的过程:
( ) ( ( ) ( ) ( ( ) ) )
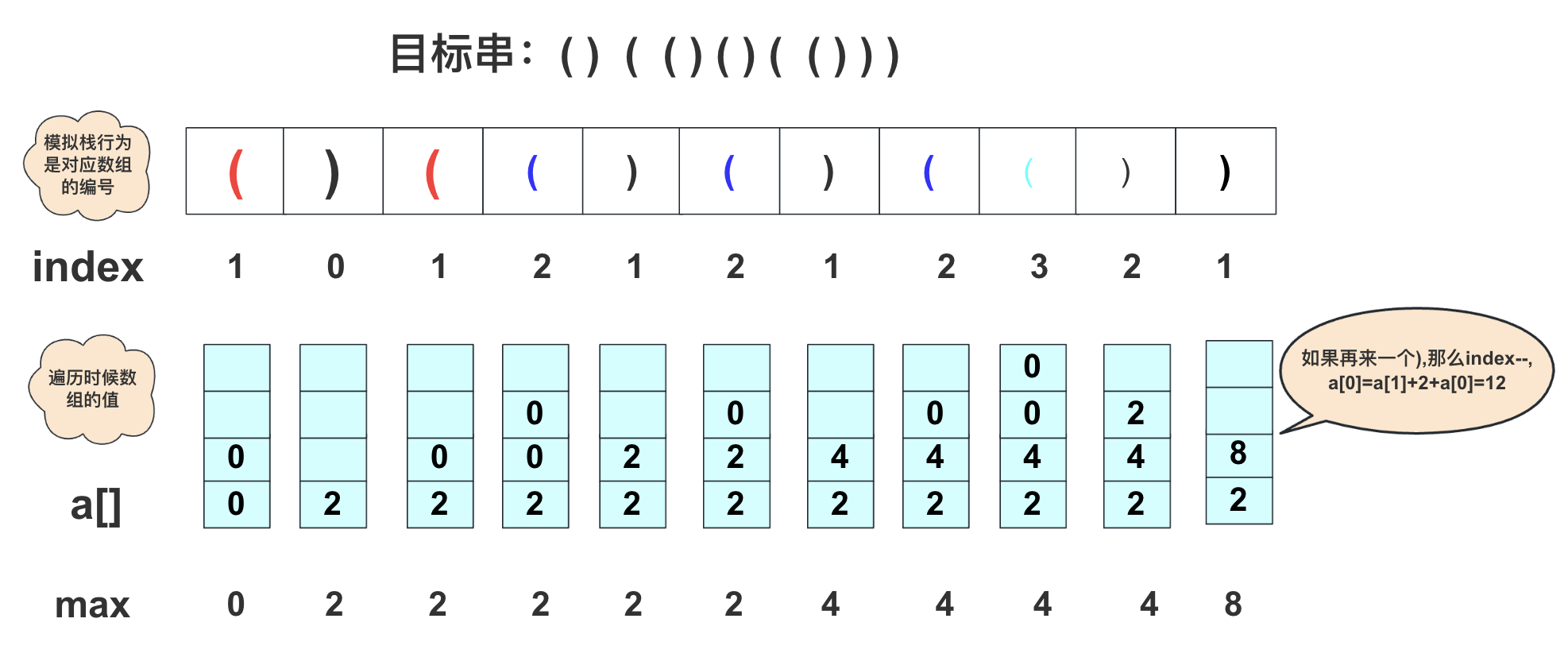
具体实现代码为:
public static int longestValidParentheses(String s) {int max = 0;int value[] = new int[s.length() + 1];int index = 0;for (int i = 0; i < s.length(); i++) {if (s.charAt(i) == '(') {index++;value[index] = 0;} else {//")"if (index == 0) {value[0] = 0;} else {value[index - 1] += value[index--] + 2;//叠加if (value[index] > max)//更新max = value[index];}}}return max;
}
用栈也可以实现,但是效率比数组略低:
public int longestValidParentheses(String s) {int maxans = 0;Stack<Integer> stack = new Stack<>();stack.push(-1);for (int i = 0; i < s.length(); i++) {if (s.charAt(i) == '(') {//(将当前的 stack.push(i);} else {stack.pop();if (stack.empty()) {stack.push(i);} else {//i-stack.peek就是i是出现的总个数 peek是还没匹配的个数maxans = Math.max(maxans, i - stack.peek());}}}return maxans;
}
总结
到这里,本文对栈的介绍就结束了,相信你可以手写个栈并且可以小试牛刀解决括号匹配问题!当然栈能解决的问题还有很多比如接雨水问题、二叉树非递归遍历等等,有些重要的还会再总结。
系列仓库地址:https://github.com/javasmall/bigsai-algorithm
csdn专栏:数据结构与算法专栏
写一篇原创不易,还请点赞、收藏、关注三连支持一下!
相关文章:

后入能先出,一文搞懂栈
目录 什么是栈数组实现链表实现栈能这么玩总结 什么是栈 栈在我们日常编码中遇到的非常多,很多人对栈的接触可能仅仅局限在 递归使用的栈 和 StackOverflowException,栈是一种后进先出的数据结构(可以想象生化金字塔的牢房和生化角斗场的狗洞)。 栈&…...
京东API接口的应用场景:商品信息查询,商品详情获取
京东API接口的应用场景涵盖了电商业务的各个方面,通过API的方式,开发者可以方便地获取京东平台上的商品信息、用户信息、订单信息等,进而进行个性化的应用开发。以下是几个典型的应用场景: 商品信息查询:通过京东API接…...

微信小程序使用iconfont坑
下载解压 font-face {font-family: "iconfont"; /* Project id 4322044 */src: url(iconfont.woff2?t1699515502419) format(woff2),url(iconfont.woff?t1699515502419) format(woff),url(iconfont.ttf?t1699515502419) format(truetype); }.iconfont {font-famil…...

最新Cocos Creator 3.x 如何动态修改3D物体的透明度
Cocos Creator 3.x 的2D UI有个组件UIOpacity组件可以动态修改UI的透明度,非常方便。很多同学想3D物体上也有一个这样的组件来动态的控制与修改3D物体的透明度。今天基于Cocos Creator 3.8 来实现一个可以动态修改3D物体透明度的组件Opacity3D。 对啦!这里有个游戏…...
golang 2018,go 1.19安装Gin
GOPROXYhttps://mirrors.aliyun.com/goproxy/ 一致提示URL不能有点,给我整郁闷了,换了这个地址好了 但是一致提示zip的包问题,最后还是不行又换回七牛 NEWBEE! [GIN-debug] Environment variable PORT is undefined. Using por…...

常用的三角函数公式
sin 2 x cos 2 x 1 \sin ^2 x \cos ^2 x 1 sin2xcos2x1 tan x sin x cos x \tan x \dfrac{\sin x}{\cos x} tanxcosxsinx cot x 1 tan x cos x sin x \cot x \dfrac{1}{\tan x}\dfrac{\cos x}{\sin x} cotxtanx1sinxcosx sec …...

【MySQL】一文学会所有MySQL基础知识以及基本面试题
文章目录 前言 目录 文章目录 前言 一、主流数据库以及如何登陆数据库 二、常用命令使用 三、SQL分类 3.1 存储引擎 四、创建数据库如何设置编码等问题 4.1操纵数据库 4.2操纵表 五、数据类型 六、表的约束 七、基本查询 八、函数 九、复合查询 十、表的内连和外连 十一、索引…...
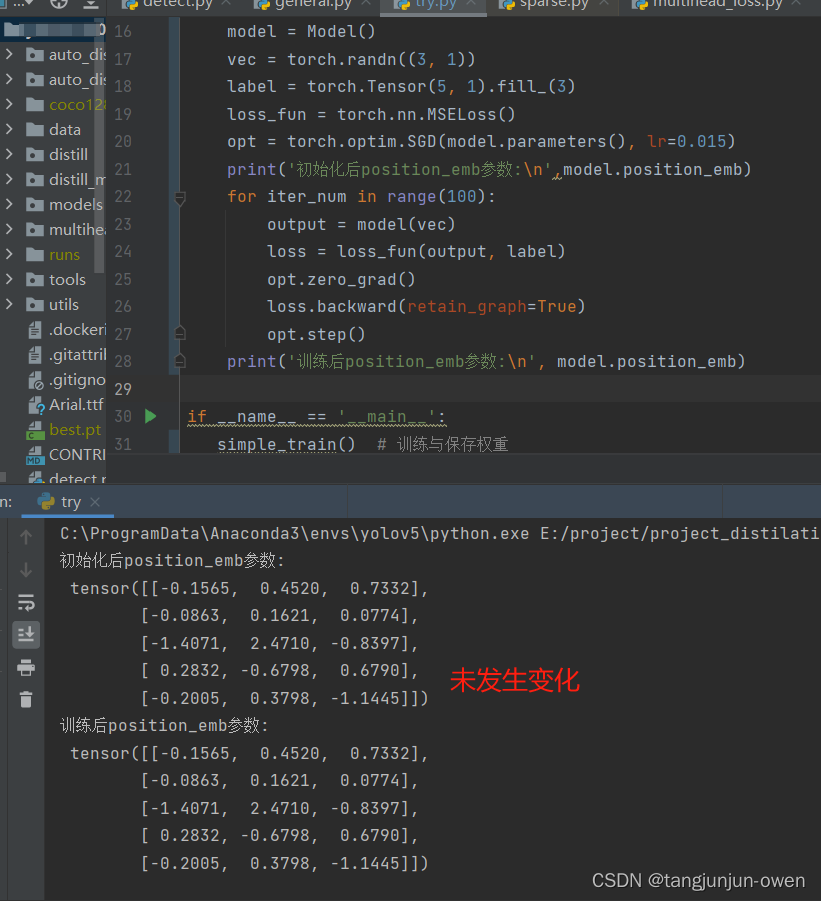
self.register_buffer方法使用解析(pytorch)
self.register_buffer就是pytorch框架用来保存不更新参数的方法。 列子如下: self.register_buffer("position_emb", torch.randn((5, 3)))第一个参数position_emb传入一个字符串,表示这组参数的名字,第二个就是tensor形式的参数…...
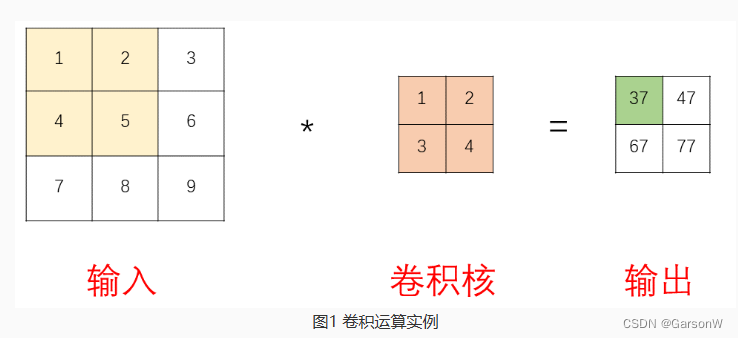
关于卷积神经网络中如何计算卷积核大小(kernels)
首先需要说明的一点是,虽然卷积层得名于卷积( convolution )运算,但我们通常在卷积层中使用更加直观的计算方式,叫做互相关( cross-correlation )运算。 也就是说,其实我们现在在这里…...
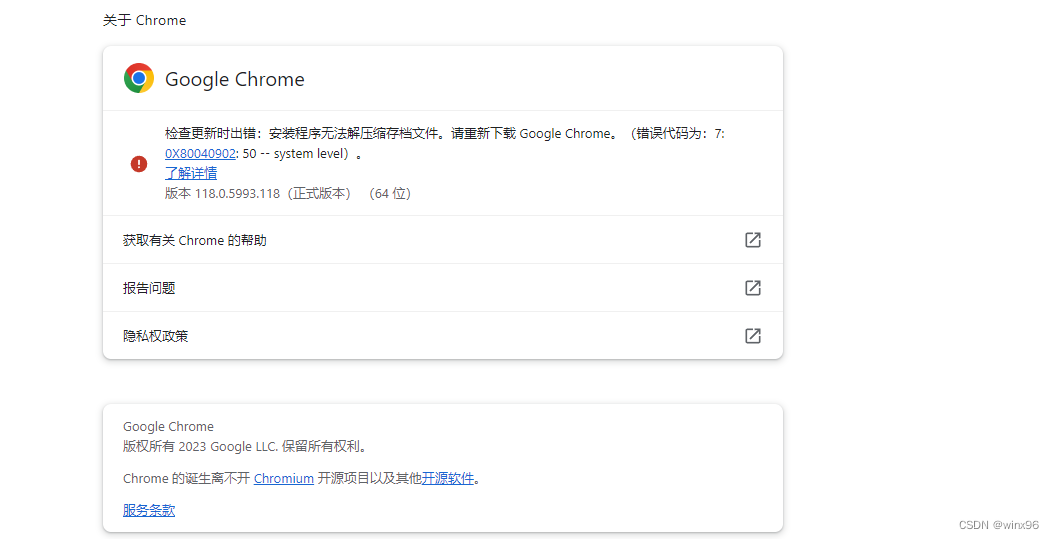
python使用selenium做自动化,最新版Chrome与chromedriver不兼容
目前Chrome版本是118.0.5993.118 下方是版本对应的下载地址: chrome版本118: https://download.csdn.net/download/qq_35845339/88510476 chrome版本119: chromedriverlinux64https://edgedl.me.gvt1.com/edgedl/chrome/chrome-for-testin…...

算法进阶指南图论 通信线路
通信线路 思路:我们考虑需要升级的那条电缆的花费,若其花费为 w ,那么从 1 到 n 的路径上,至多存在 k 条路径的价值大于 w ,这具有一定的单调性,当花费 w 越大,我们路径上价值大于 w 的花费会越…...
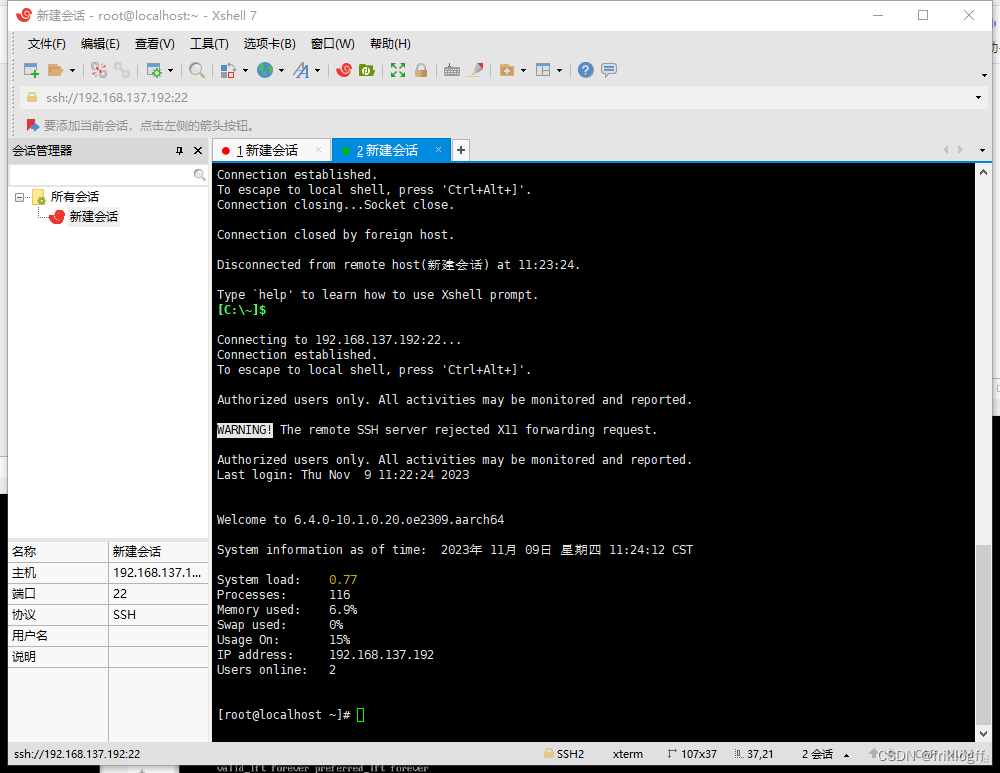
【QEMU-tap-windows-Xshell】QEMU 创建 aarch64虚拟机(附有QEMU免费资源)
“从零开始:在Windows上创建aarch64(ARM64)虚拟机” 前言 aarch64(ARM64)架构是一种现代的、基于 ARM 技术的计算架构,具有诸多优点,如低功耗、高性能和广泛应用等。为了在 Windows 平台上体验…...

strtok函数详解:字符串【分割】的利器
目录 一,strtok函数简介 二,strtok函数的用法 三,strtok函数的注意事项 一,strtok函数简介 strtok函数可以帮助我们将一个字符串按照指定的分隔符进行分割,从而得到我们想要的子字符串。 🍂函数头文件&am…...

winui3开发笔记(二)自定义标题栏
参考文章链接:https://www.programminghunter.com/article/46392310600/ 注意事项 获取 AppWindowTitleBar 的实例并设置其颜色属性时,InitializeTitleBar(AppWindow.TitleBar);,只适用于Windows App SDK 1.2及以上,所以如果用w…...

MapReduce 读写数据库
MapReduce 读写数据库 经常听到小伙伴吐槽 MapReduce 计算的结果无法直接写入数据库, 实际上 MapReduce 是有操作数据库实现的 本案例代码将实现 MapReduce 数据库读写操作和将数据表中数据复制到另外一张数据表中 准备数据表 create database htu; use htu; creat…...
)
设计模式 -- 状态模式(State Pattern)
状态模式:类的行为基于它的状态改变 属于行为型模式,创建表示各种状态的对象和一个行为随着状态对象改变而改变的 context 对象。在代码中包含大量与对象状态有关的条件语句可以通过此模式将各种具体的状态类抽象出来 介绍 意图:允许对象在…...

qt quick发布程序启动失败
qt quick/qml 程序发布之后,程序启动不了 经过探究测试,程序启动的不了的情况下是因为有dll没有添加。在release文件夹下进行发布操作(不单独复制xx.exe拿出来),再次点击IDE的RUN按钮,则会提示有Moudle没有…...

nginx反向代理报错合集
本文汇集了最近在使用nginx反向代理过程中遇到的一系列错误及其解决办法。 1缺乏支持项导致nginx配置错误 在利用sudo ./configure --with-http_ssl_module --with-http_stub_status_module进行配置时,往往会遇到以下类型的错误 error: the HTTP rewrite module …...

【Linux精讲系列】——vim详解
作者主页 📚lovewold少个r博客主页 ⚠️本文重点:c入门第一个程序和基本知识讲解 👉【C-C入门系列专栏】:博客文章专栏传送门 😄每日一言:宁静是一片强大而治愈的神奇海洋! 目录 目录 作者…...

微信小程序自动化采集方案
本文仅供学习交流,只提供关键思路不会给出完整代码,严禁用于非法用途,拒绝转载,若有侵权请联系我删除! 一、引言 1、对于一些破解难度大,花费时间长的目标,我们可以先采用自动化点击触发请求&…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
