【C++】AVL树的4中旋转调整
文章目录
- 前提
- 一、AVL树的结构定义
- 二、AVL的插入(重点)
- 1. 插入的结点在较高左子树的左侧(右单旋)
- 2. 新节点插入较高右子树的右侧(左单旋)
- 3.新结点插入较高右子树的左侧(先右单旋再左单旋)
- 4. 新节点插入较高左子树的右侧(先左单旋再右单旋)
- 插入的整体代码
前提
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查 找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年发明了一种解决上述问题的方法:
当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(-1、0、1),即可降低树的高度,从而减少平均搜索长度。
由此,该树被称为AVL树,即两位科学家名字的第一个字母。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树的高度差(简称平衡因子)的绝对值不超过1
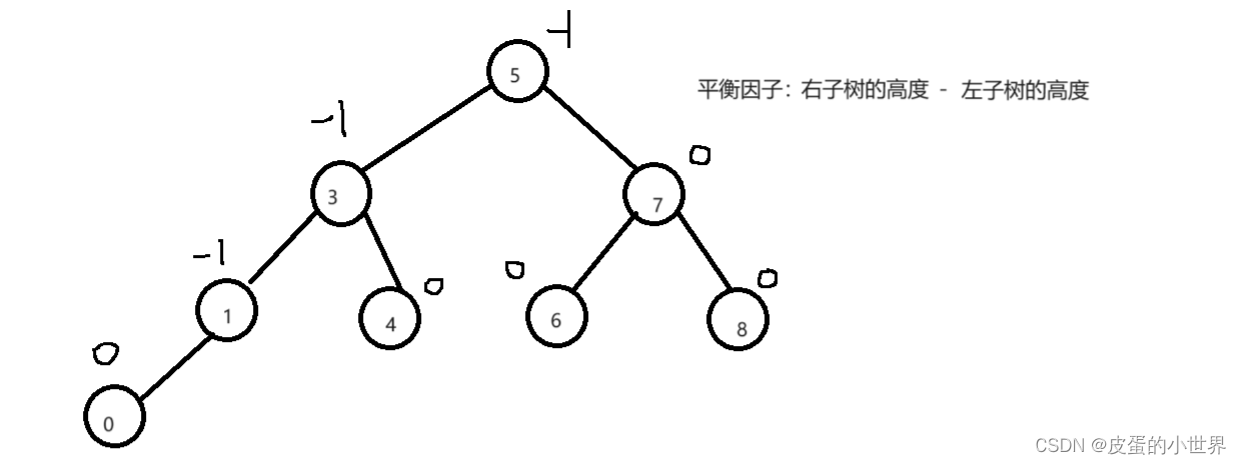
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(logN),搜索时间复杂度O(logN)。
提示:以下是本篇文章正文内容,下面案例可供参考
一、AVL树的结构定义
树节点的结构创建:
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv; //键值对来存储 K AND Vint _bf;//平衡因子//AVL树并没有规定必须要选择设计平衡因子,只是一个实现的选择,方便控制//构造函数AVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}};
树的框架创建:
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node; //结点typedef
public:
//......
private:Node* _root = nullptr;
};
二、AVL的插入(重点)
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
(寻找位置->创建结点->插入节点->更新平衡因子->调整子树->形成AVL树)
1. 插入的结点在较高左子树的左侧(右单旋)
这样会造成parent的平衡因子变成-2, 当前节点(不是新增节点)的平衡因子变成-1
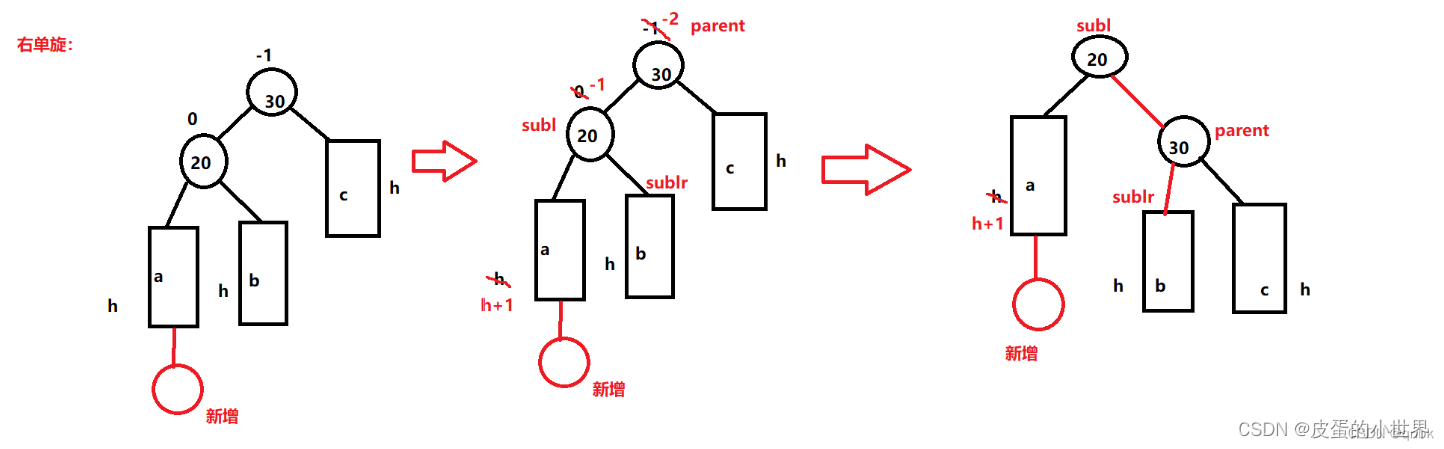
//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* pParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (pParent == nullptr){_root = subL;_root->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subL;}else pParent->_right = subL;subL->_parent = pParent;}// 更新平衡因子parent->_bf = subL->_bf = 0;}2. 新节点插入较高右子树的右侧(左单旋)
这样会造成parent的平衡因子变成2,当前节点(不是新增节点)的平衡因子变成1
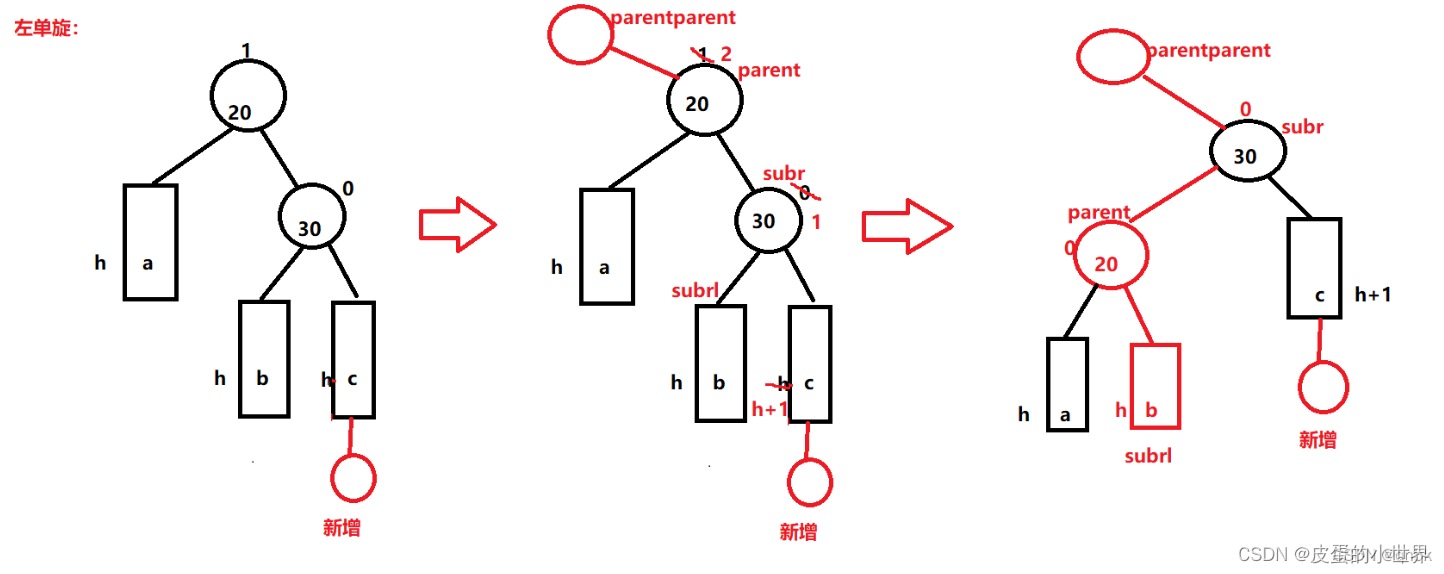
//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* pParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (pParent == nullptr){_root = subR;_root->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subR;}else pParent->_right = subR;subR->_parent = pParent;}//更新平衡因子subR->_bf = parent->_bf = 0;}
3.新结点插入较高右子树的左侧(先右单旋再左单旋)
会造成parent的平衡因子变成2, 当前节点(不是新增节点)平衡因子变成-1
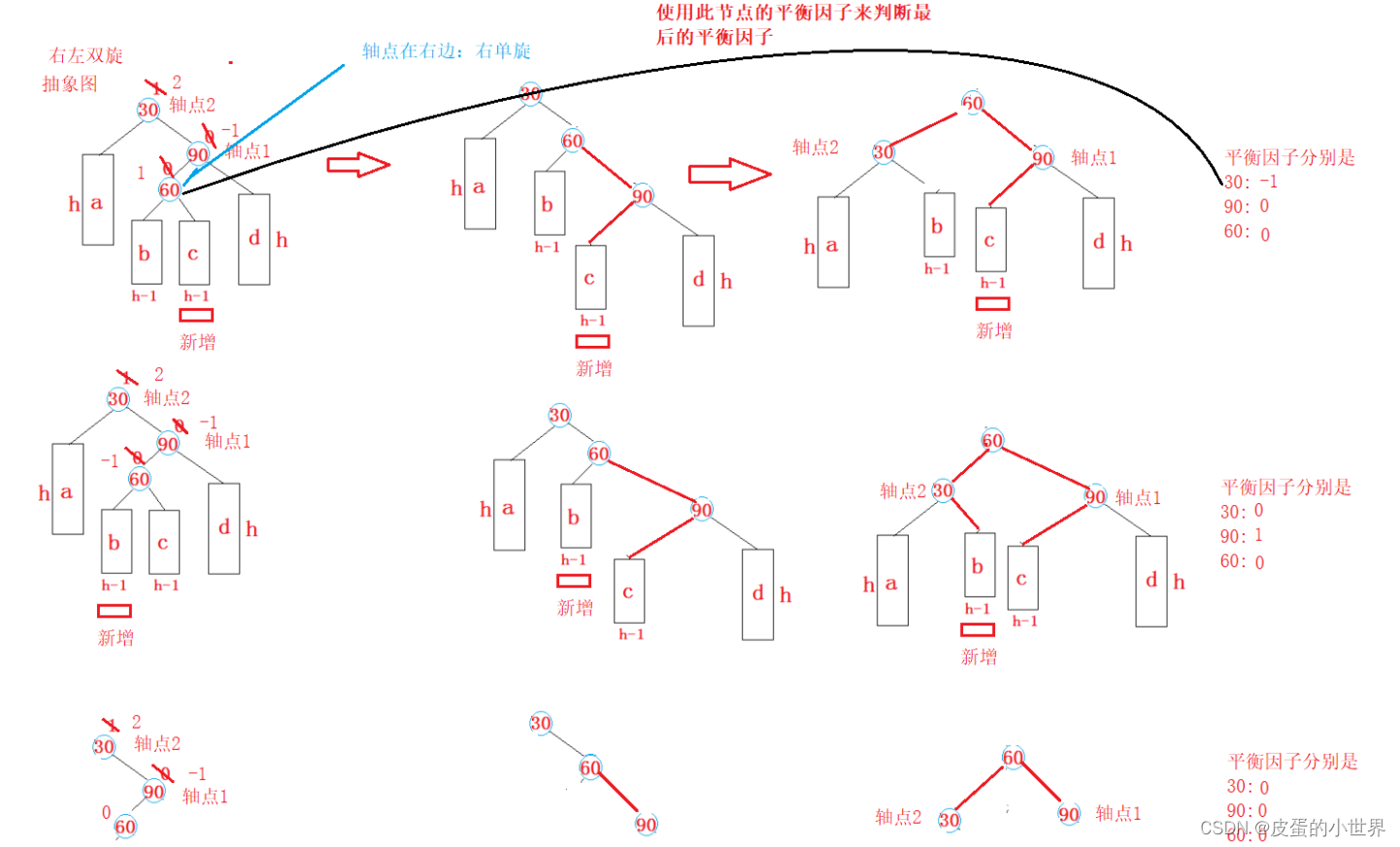
void RotateRL(Node* parent){Node* subR = parent->_right; //左子树60Node* subRL = subR->_left;// 右子树的左子树90int bf = subRL->_bf;// 记录SubRLd 平衡因子// 先以SubR为轴进行右单旋RotateR(parent->_right);// 再进行左单旋RotateL(parent);if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else assert(0);}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 1){subL->_bf = -1;parent->_bf = 0;subLR->_bf = 0;}else assert(0);}
4. 新节点插入较高左子树的右侧(先左单旋再右单旋)
这样会造成parent的平衡因子变成-2, 当前结点的平衡因子变成1
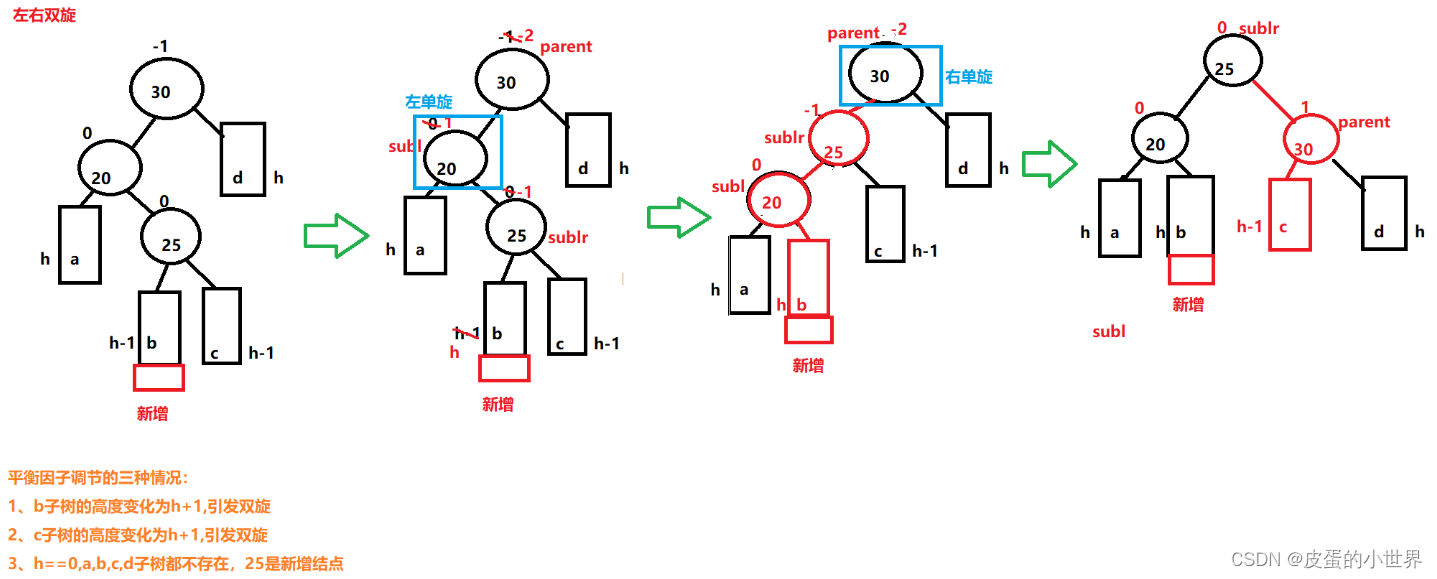
void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 1){subL->_bf = -1;parent->_bf = 0;subLR->_bf = 0;}else assert(0);}
插入的整体代码
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;//parent是cur的父节点Node* cur = _root;//cur往下走while (cur){if (cur->_kv.first > kv.first)//我比你小,往左找{parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first)//我比你大,往右找{parent = cur;cur = cur->_right;}else{return false;//AVL树不允许有重复值}}//走到这里就表示找到我们要插入kv值的正确位置了,准备插入节点..........cur = new Node(kv);if (parent->_kv.first < kv.first)//如果new的节点比父节点大,那么父节点的右指针指向new节点{parent->_right = cur;cur->_parent = parent;}else//如果new的节点比父节点小,那么父节点的左指针指向new节点{parent->_left = cur;cur->_parent = parent;}//开始更新平衡因子while (parent)//更新到根节点才算更新完平衡因子{//1、如果是右子树新增结点,那么父节点的_bf就加一//2、如果是左子树新增结点,那么父节点的_bf就减一//+1和-1大家可以自己决定,只要是对的,怎么都行!if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}// 是否继续更新依据:子树的高度是否变化// 1、parent->_bf == 0说明之前parent->_bf是 1 或者 -1// 说明之前parent一边高一边低,这次插入填上矮的那边,parent所在子树高度不变,不需要继续往上更新// 2、parent->_bf == 1 或 -1 说明之前是parent->_bf == 0,两边一样高,现在插入一边更高了,// parent所在子树高度变了,继续往上更新// 3、parent->_bf == 2 或 -2,说明之前parent->_bf == 1 或者 -1,现在插入严重不平衡,违反规则// 就地处理--旋转// 旋转:// 1、让这颗子树左右高度不超过1// 2、旋转过程中继续保持他是搜索树// 3、更新调整孩子节点的平衡因子// 4、让这颗子树的高度跟插入前保持一致//如果新增节点cur,使得父节点parent的平衡因子变成了0,那么表示该插入节点对整棵树的平衡因子没有影响//不用向上判断,可以直接退出if (parent->_bf == 0){break;}//如果新增cur使得父节点parent的平衡因子变成了1或者-1,那么我们要继续向上判断是否对上面的节点的//说明之前的平衡被打破,子树的高度变化了,有可能会造成父节点的平衡因子出现问题else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}//当平衡因子出现2 or -2 的时候就需要调整子树else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1)//左旋{RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1)//右旋{RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1)//左右旋{RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1)//右左旋{RotateRL(parent);}else{assert(false);}break;//旋转完一次就可以退出了,因为旋转的时候我们已经向上判断了,除非新插入,否则树就是avl树}else{assert(false);//这里直接报错,走到这里树就已经不是AVL树了}}return true;
}相关文章:

【C++】AVL树的4中旋转调整
文章目录 前提一、AVL树的结构定义二、AVL的插入(重点)1. 插入的结点在较高左子树的左侧(右单旋)2. 新节点插入较高右子树的右侧(左单旋)3.新结点插入较高右子树的左侧(先右单旋再左单旋&#x…...
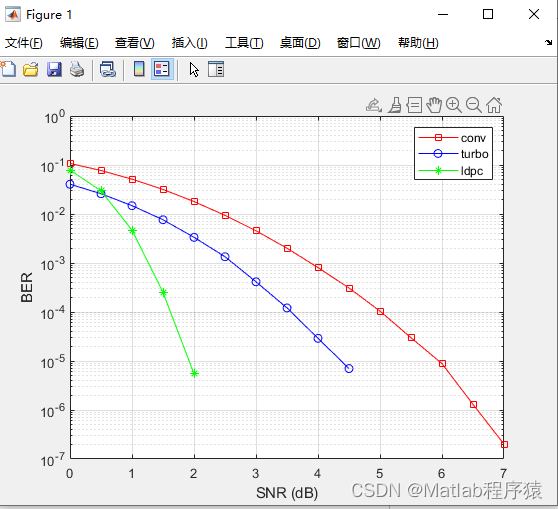
【MATLAB源码-第69期】基于matlab的LDPC码,turbo码,卷积码误码率对比,码率均为1/3,BPSK调制。
操作环境: MATLAB 2022a 1、算法描述 本文章介绍了卷积码、Turbo码和LDPC码。以相同的码率仿真这三种编码,并对比其误码率性能 信源输出的数据符号(二进制)是相互独立和等概率的; 信道是加性白高斯噪声信道&#…...

Java获取时间戳、字符串和Date对象的相互转换、日期时间格式化、获取年月日
获取时间戳(自1970年1月1日经历的毫秒数值) package org.example;import java.util.Date;public class Main {public static void main(String[] args) {Date date1 new Date(1699540662210L);System.out.println(date1.getTime());Date date2 new Dat…...

用c语言实现矩阵转置
下面是在 C 语言中实现矩阵转置的示例代码: #include <stdio.h> #define ROWS 3 #define COLS 3 void transpose(int matrix[ROWS][COLS]) { int temp; for(int i0; i<ROWS; i) { for(int j0; j<i; j) { temp matrix[i][j]; matrix[i][j] matrix[j]…...
)
蓝桥杯官网练习题(移动距离)
题目描述 X 星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为 1,2,3, 当排满一行时,从下一行相邻的楼往反方向排号。 比如:当小区排号宽度为 6 时,开始情形如下: 1 2 3 4 5 6 12 …...
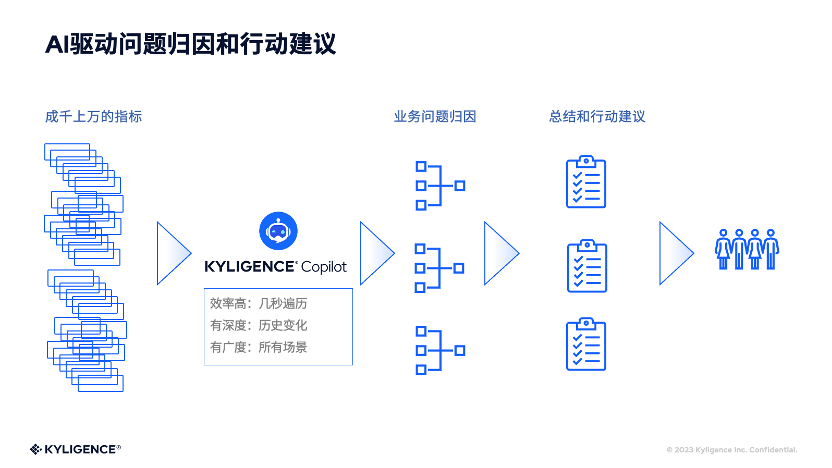
不止于“初见成效”,阿斯利康要让数据流转,以 AI 带动决策智能
“阿斯利康数字化成果在进博会上引人注目,令我感到非常高兴。”这是阿斯利康代表的感慨。 数字化建设目标是利用先进技术来提高企业运营效率,降低成本。在第六届进博会的7.2 B2-01展区,阿斯利康不仅展示了全球领先的生物医药和医疗器械成果&a…...
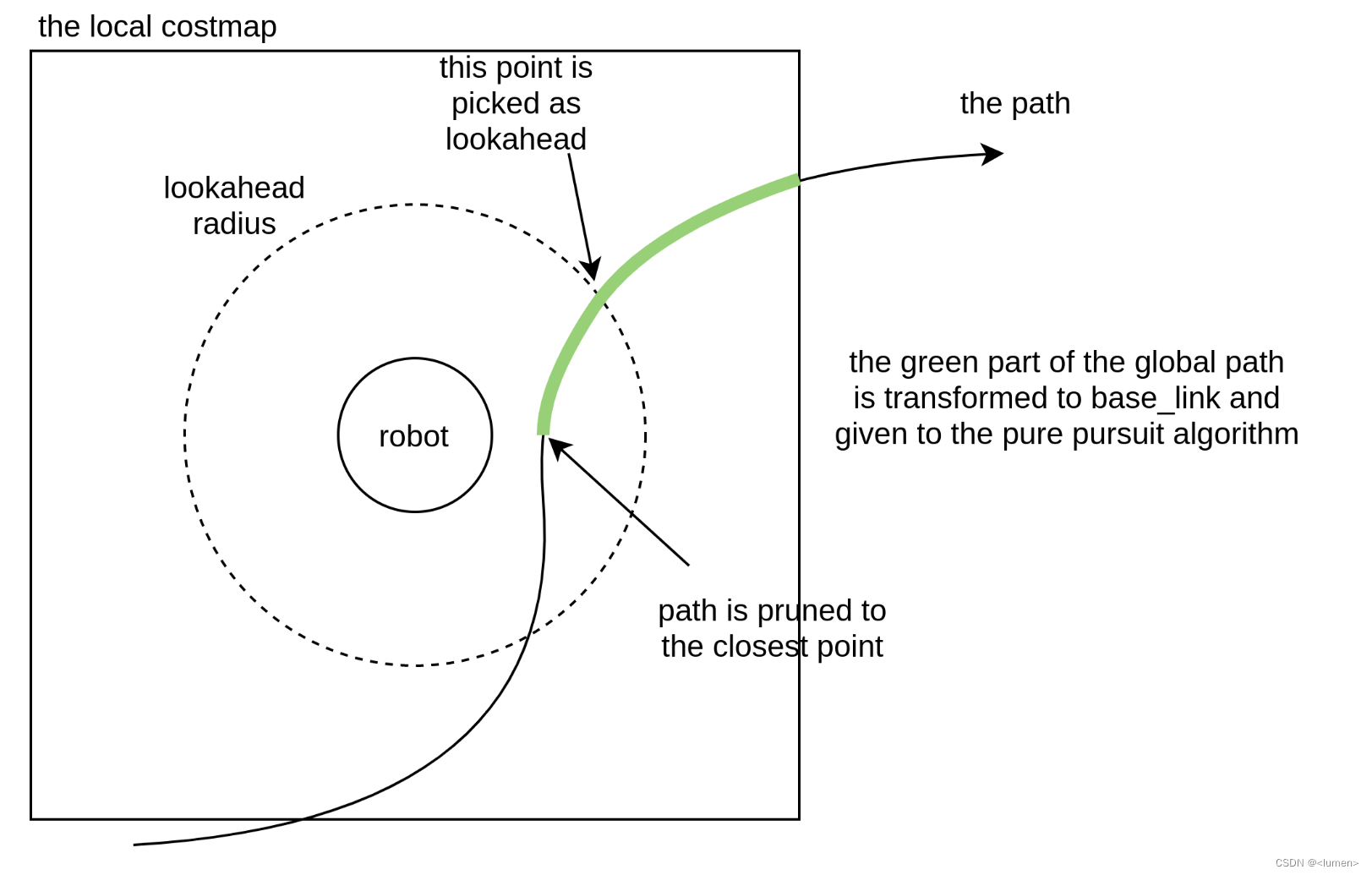
nav2 调节纯追踪算法
纯追踪算法 纯追踪基础 The core idea is to find a point on the path in front of the robot and find the linear and angular velocity to help drive towards it. 核心思想是在机器人前方的路径上找到一个点,并找到一个合适的线速度和角速度,以驱…...
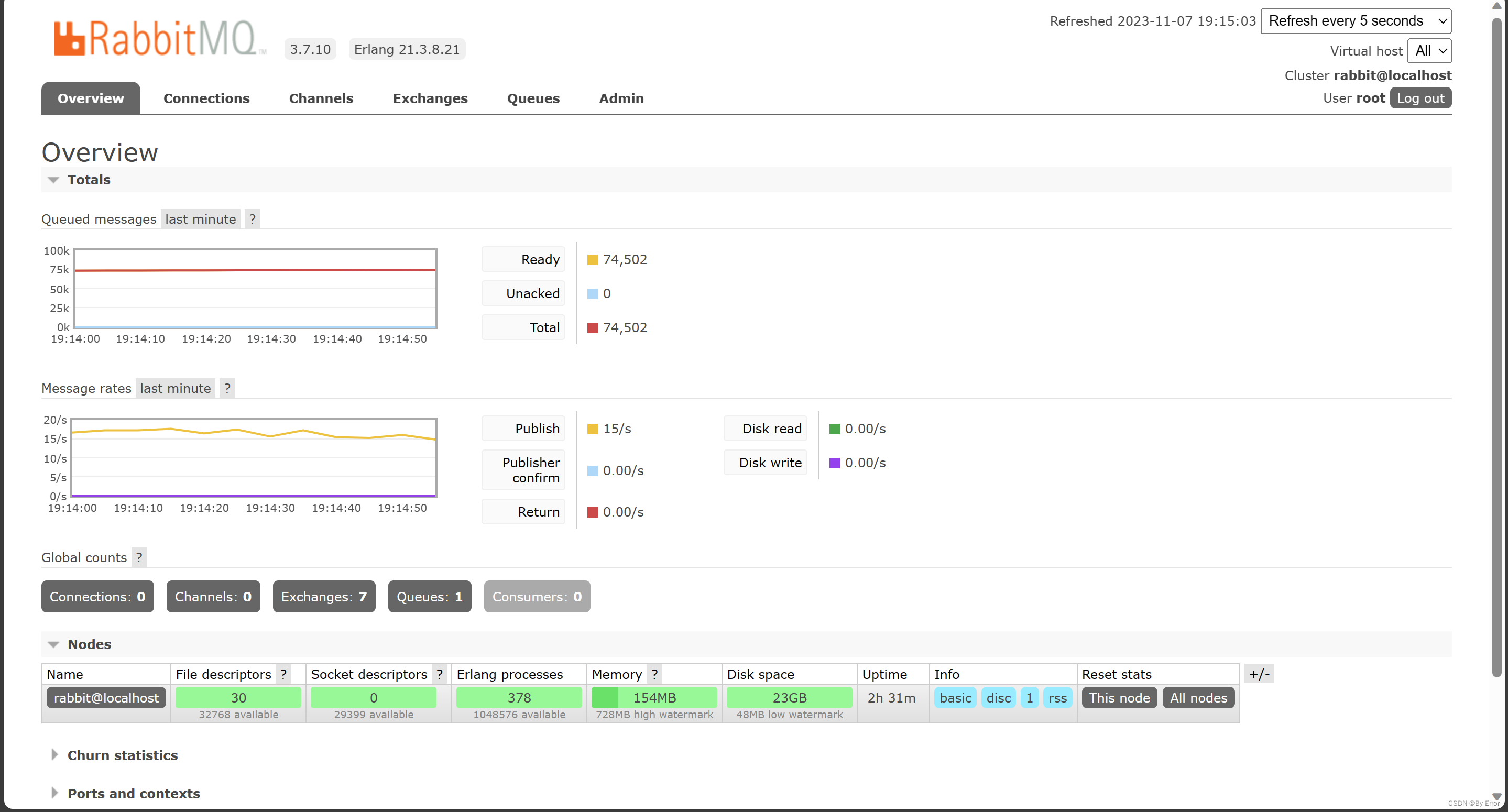
安装RabbitMQ
安装RabbitMQ 下载需要的两个包 # 这直接就可以安装了,下面 ‘上传对应的rmp包’ 操作 [rootrabbitmq-1 ~]# curl -s https://packagecloud.io/install/repositories/rabbitmq/erlang/script.rpm.sh | sudo bash [rootrabbitmq-1 ~]# yum install erlang-21.3.8.2…...
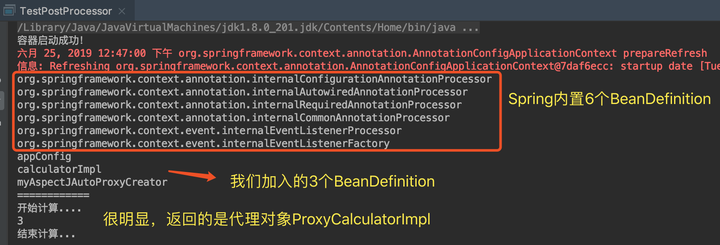
Spring基础(1):两个概念
最近看了点Spring的源码,于是来稍微扯一扯,希望能帮一部分培训班出身的朋友撕开一道口子,透透气。 广义上的Spring指的是Spring整个项目,包含SpringBoot、SpringCloud、SpringFramework、SpringData等等, 本系列文章…...

国产化精密划片机已得到国内更多厂家青睐
国产化精密划片机在近年来得到了国内许多厂家的青睐,这是因为精密划片机在工业生产中有着重要作用。这种设备主要用于高精密切割加工,适用于多种材料,包括硅、石英、氧化铝、氧化铁等。 以精密晶圆划片机为例,这种设备采用了自主研…...

Voice Control for ChatGPT简单高效的与ChatGPT进行交流学习。
快捷又不失灵活性 日常生活中,我们与亲人朋友沟通交流一般都是喜欢语音的形式来完成的,毕竟相对于文字来说语音就不会显的那么的苍白无力,同时最大的好处就是能解放我们的双手吧,能更快实现两者间的对话,沟通便更高效…...

flutter生态一统甜夏 @Android @ios @windowse @macos @linux @Web
(愿景)G o o g l e 中 国flutter生态一统天下(IT) Web Android ios Windowse Macos Linux Google中国https://space.bilibili.com/64169458 https://pub-web.flutter-io.cn 构建 Flutter Web 应用 构建 Flutter Web 应用 - Flutter 中文文档 - Flutter 中文开发者网站 …...

计算机基础知识49
三板斧的使用(views.py) 三个方法:HttpResponse: 返回的是字符串render : 返回html文件redirect : 返回加载HTML页面的 def html(request):print(from html)# return HttpResponse(request) # 它返回的是字符串return render(request,html.html) # 返回html# ret…...
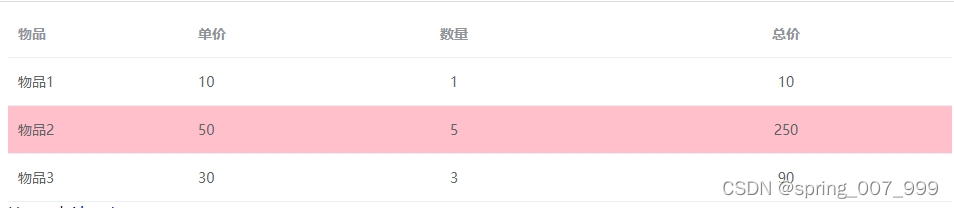
el-table给某一行加背景色
数据列表中总价大于100的一行背景色为红色,效果图如下: 代码示例: <template><div id"app"><!-- 测试区域!!!!!!!!&am…...

搭建 Makefile+OpenOCD+CMSIS-DAP+Vscode arm-none-eabi-gcc 工程模板
STM32F407-GCC-Template Arm-none-eabi-gcc MakefileOpenOCDCMSIS-DAPVscode工程模板 一、本次环境搭建所用的软硬件 1)Windows or Linux (本文以Windows为主) 2)JLink、Daplink、Wch-Link烧录器 3)GNU Arm Embedded Toolchain交叉编译…...
格式的测试)
Unity场景ab包加载压缩(LZ4,LZMA)格式的测试
情况 最近场景越来越大,大概800M的场景加载时间可能长达40秒左右,所以需要测试看看发生了什么。 测试环境 测试环境Win10,21thI5-12600KF,32GRam , Nvidia GF RTX2060 32G Scene1大小:741M 加载代码 首…...
私有化部署大模型:5个.Net开源项目
从零构建.Net前后端分离项目 今天一起盘点下,10月份推荐的5个.Net开源项目(点击标题查看详情)。 1、BootstrapBlazor企业级组件库:前端开发的革新之路 BootstrapBlazor是一个用于构建现代Web应用程序的开源框架,它基…...
安卓系统手机便签app使用哪一款?
在现代快节奏的生活中,我们经常会遇到各种繁忙的事务和容易遗忘的备忘事项。为避免大家遗忘重要的事情,大家可以在常用的手机上安装记录备忘事项的工具,为了帮助安卓用户高效地记录和管理这些信息,今天我将向大家推荐一款功能强大…...
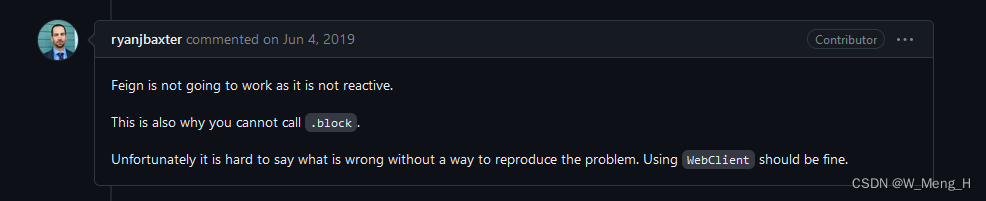
SpringCloud-Gateway无法使用Feign服务(2021.X版本)
Spring Cloud Gateway 2021.x版本,无法使用Feign调用其他服务接口。 问题原因: 在官网的 issue 里面找到了相关的问题。 How to call another micro-service on GatewayFilterFactory ? Issue #1090 spring-cloud/spring-cloud-gateway GitHubHel…...
基于SSM的建筑装修图纸管理平台
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
