【算法与数据结构】39、LeetCode组合总和
文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
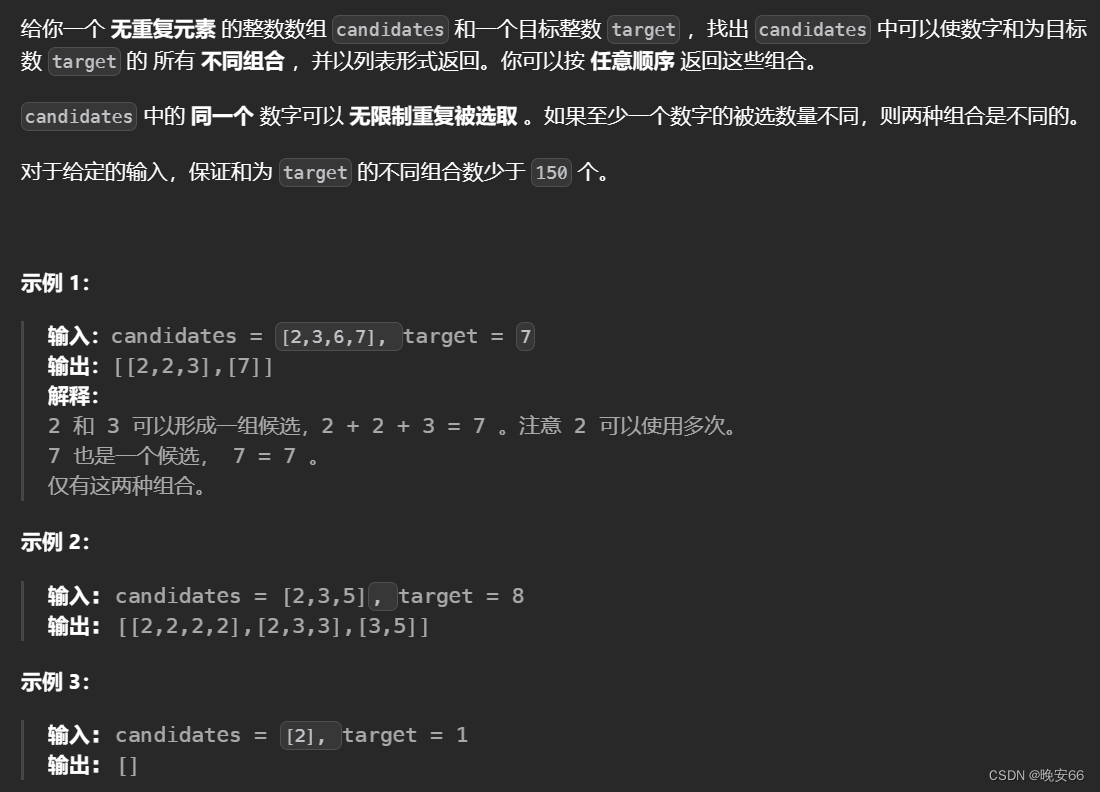
二、解法
思路分析:这道题当中数字可以多次使用,那么我们在递归语句当中不能直接找下一个candidate的元素,需要不断累加重复元素,直到它>=target,才能进入下一个循环,同时需要做剪枝优化,循环只在这个条件下进行sum+candidates[i] <= target。这道题的框架基于【算法与数据结构】216、LeetCode组合总和 III修改。
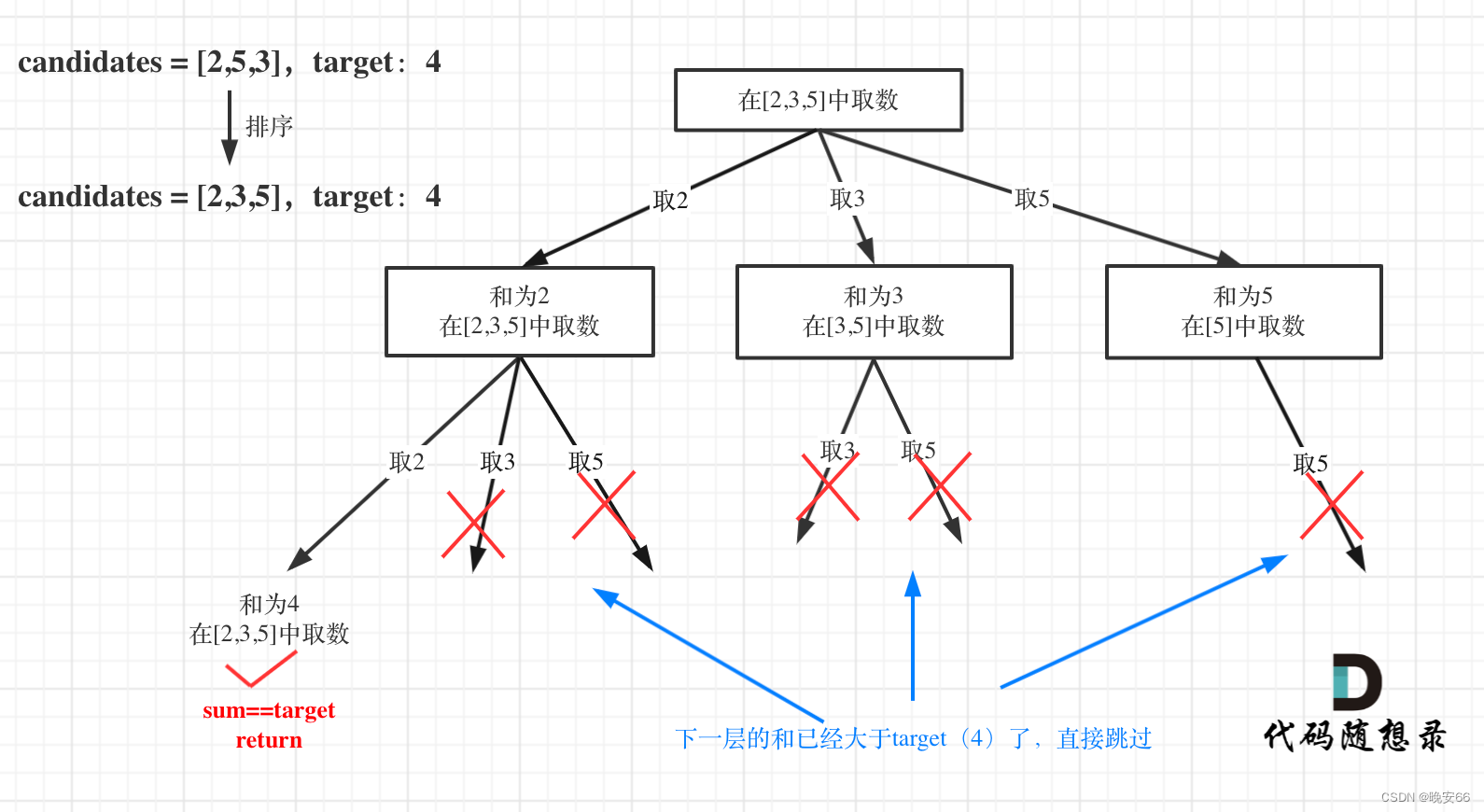
程序如下:
class Solution {
private:vector<vector<int>> result; // 结果合集vector<int> path;void backtracking(const vector<int>& candidates, const int target, int sum, int startIndex) {if (sum > target) return; // 剪枝if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum+candidates[i] <= target; i++) { // 剪枝优化sum += candidates[i];path.push_back(candidates[i]); // 处理节点backtracking(candidates, target, sum, i); // 递归sum -= candidates[i];path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<int> nums = candidates; // 对candidates数组升排序sort(nums.begin(), nums.end());backtracking(nums, target, 0, 0);return result;}
};
复杂度分析:
- 时间复杂度: O ( n ∗ 2 n ) O(n*2^n) O(n∗2n)。
- 空间复杂度: O ( t a r g e t ) O(target) O(target)。
三、完整代码
# include <iostream>
# include <string>
# include <vector>
# include <algorithm>
using namespace std;class Solution {
private:vector<vector<int>> result; // 结果合集vector<int> path;void backtracking(const vector<int>& candidates, const int target, int sum, int startIndex) {if (sum > target) return; // 剪枝if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum+candidates[i] <= target; i++) { // 剪枝优化sum += candidates[i];path.push_back(candidates[i]); // 处理节点backtracking(candidates, target, sum, i); // 递归sum -= candidates[i];path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<int> nums = candidates; // 对candidates数组升排序sort(nums.begin(), nums.end());backtracking(nums, target, 0, 0);return result;}
};int main() {vector<int> candidates = { 2, 3, 6, 7 };int target = 7;Solution s1;vector<vector<int>> result = s1.combinationSum(candidates, target);for (vector<vector<int>>::iterator it = result.begin(); it != result.end(); it++) {for (vector<int>::iterator jt = (*it).begin(); jt != (*it).end(); jt++) {cout << *jt << " ";}cout << endl;}system("pause");return 0;
}
end
相关文章:

【算法与数据结构】39、LeetCode组合总和
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:这道题当中数字可以多次使用,那么我们在递归语句当中不能直接找下一个candidate的元素&…...

行政大厅满意度调查内容
行政大厅满意度调查的内容应该涵盖各个方面,以全面了解公众对行政大厅服务的满意度和意见。以下是可能包含在行政大厅满意度调查中的内容: 服务态度: 行政大厅工作人员的友好程度和专业水平。是否受到尊重和礼貌的待遇。 办事效率…...
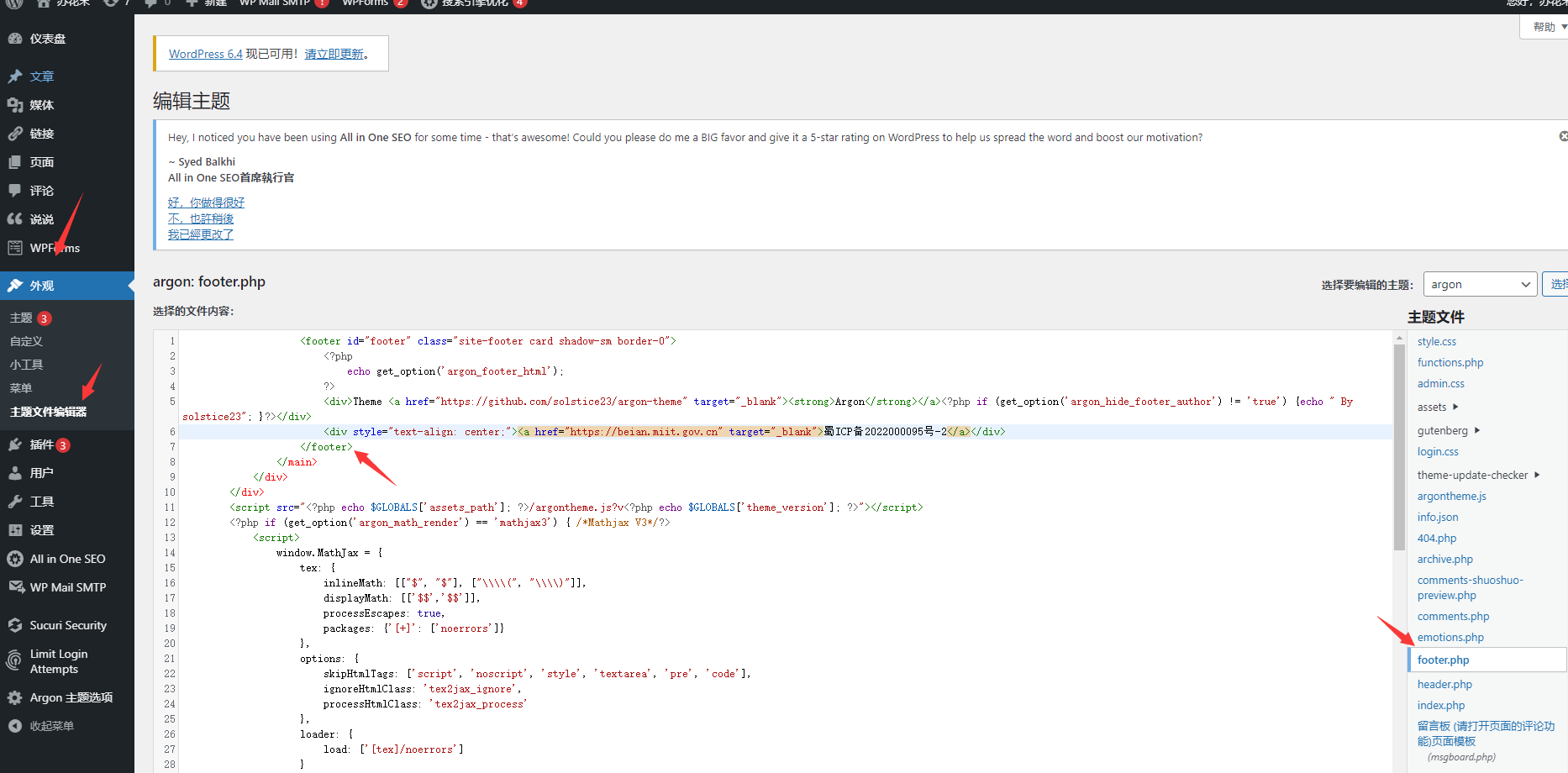
WordPress页脚配置备案号
进入后台管理页面 后台管理页面地址一般是:域名/wp-admin 在指定位置加入代码 点击外观 -> 主题文件编辑器 在右侧的文件中选择 footer.php,[注意:上方的主题需要是你自己选择的对应的主题]在 </footer>标签这一行的上一行中加入代码 <di…...

时间序列预测模型实战案例(十)(个人创新模型)通过堆叠CNN、GRU、LSTM实现多元预测和单元预测
本文介绍 本篇博客为大家讲解的是通过组堆叠CNN、GRU、LSTM个数,建立多元预测和单元预测的时间序列预测模型,其效果要比单用GRU、LSTM效果好的多,其结合了CNN的特征提取功能、GRU和LSTM用于处理数据中的时间依赖关系的功能。通过将它们组合在…...

【有源码】基于uniapp的农场管理小程序springboot基于微信小程序的农场检测系统(源码 调试 lw 开题报告ppt)
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...

商城系统分布式下单
一、锁定库存的sql select * from ware where id{id} and total-lock>0 update ware set locklock{num} where id{id} and total-lock>{num} 二、下单服务要用分布式事务,因为seat的二阶段提交要说很多资源,会造成处理变成串行化,高并发…...
Java自学第5课:Java web开发环境概述,更换Eclipse版本
1 Java web开发环境 前面我们讲了java基本开发环境,但最终还是要转到web来的,先看下怎么搭建开发环境。 这个图就是大概讲了下开发和应用环境,其实很简单,对于一台裸机,win7 系统的,首先第1步,…...

[网鼎杯 2020 青龙组]AreUSerialz
[网鼎杯 2020 青龙组]AreUSerialz <?phpinclude("flag.php");highlight_file(__FILE__);class FileHandler {protected $op;protected $filename;protected $content;function __construct() {$op "1";$filename "/tmp/tmpfile";$content…...

使用Kotlin与Unirest库抓取音频文件的技术实践
目录 摘要 一、Kotlin与Unirest库概述 二、使用Kotlin和Unirest抓取音频文件 1、添加Unirest依赖 2、发送HTTP请求获取音频文件 3、保存音频文件 三、完整代码示例 四、注意事项 结论 摘要 本文详细阐述了如何使用Kotlin编程语言与Unirest库抓取网络上的音频文件。首…...

gdb调试常用命令
基本命令 1)进入GDB #gdb test test是要调试的程序,由gcc test.c -g -o test生成。进入后提示符变为(gdb) 。 2)查看源码 (gdb) l 源码会进行行号提示。 如果需要查看在其他文件中定义的函数,在l后加上函数名即可定位到这…...

CH11_重构API
将查询函数和修改函数分离(Separate Query from Modifier) function getTotalOutstandingAndSendBill() {const result customer.invoices.reduce((total, each) > each.amount total, 0);sendBill();return result; }function totalOutstanding() …...
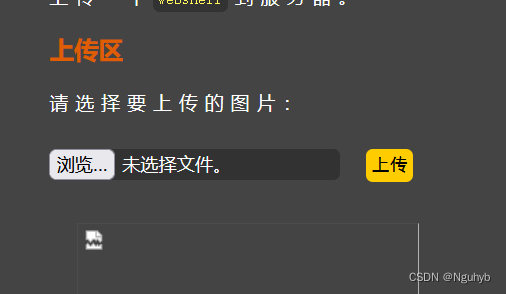
UPLOAD-LABS1
less1 (js验证) 我们上传PHP的发现不可以,只能是jpg,png,gif(白名单限制了) 我们可以直接去修改限制 在查看器中看到使用了onsubmit这个函数,触发了鼠标的单击事件,在表单提交后马上调用了re…...

WordPress相关文章推荐
首先 WordPress 本身并没有相关文章的推荐功能,网站之所以需要这样的功能出于两个原因,一方面是推荐相关的内容越优质,访客的留存和继续阅读将会增强,同样从优化角度来说会更加有利于搜索引擎抓取时对页面质量的提升,毕…...

【QML】Qt和QML获取操作系统类型
1. Qt获取系统类型 //方法 QSysInfo::productType()//举例: if(QSysInfo::productType() "windows") {qDebug() << "windows system"; }官方说明: [static] QString QSysInfo::productType() Returns the product name of …...
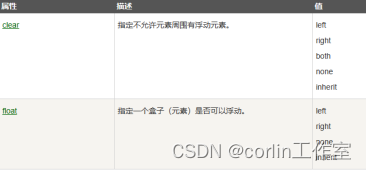
CSS 显示、定位、布局、浮动
一、CSS 显示: CSS display属性设置元素应如何显示;CSS visibility属性指定元素应可见还是隐藏。隐藏元素可以通过display属性设置为“none”,也可以通过visibility属性设置为“hidden”。两者的区别:visibility:hidden可以隐藏某…...

Java 学习笔记
文章目录 一、集合1.1 List1.1.1 ArrayList1.1.2 Vector1.1.3 LinkedList 1.2 Deque1.3 Set1.4 Map1.4.1 HashMap1.4.2 LinkedHashMap 1.5 注意事项 二、函数式接口和 Lambda 表达式三、方法引用3.1 静态方法引用3.2 实例方法引用3.2 特定类型的方法引用3.4 构造器引用 四、Str…...
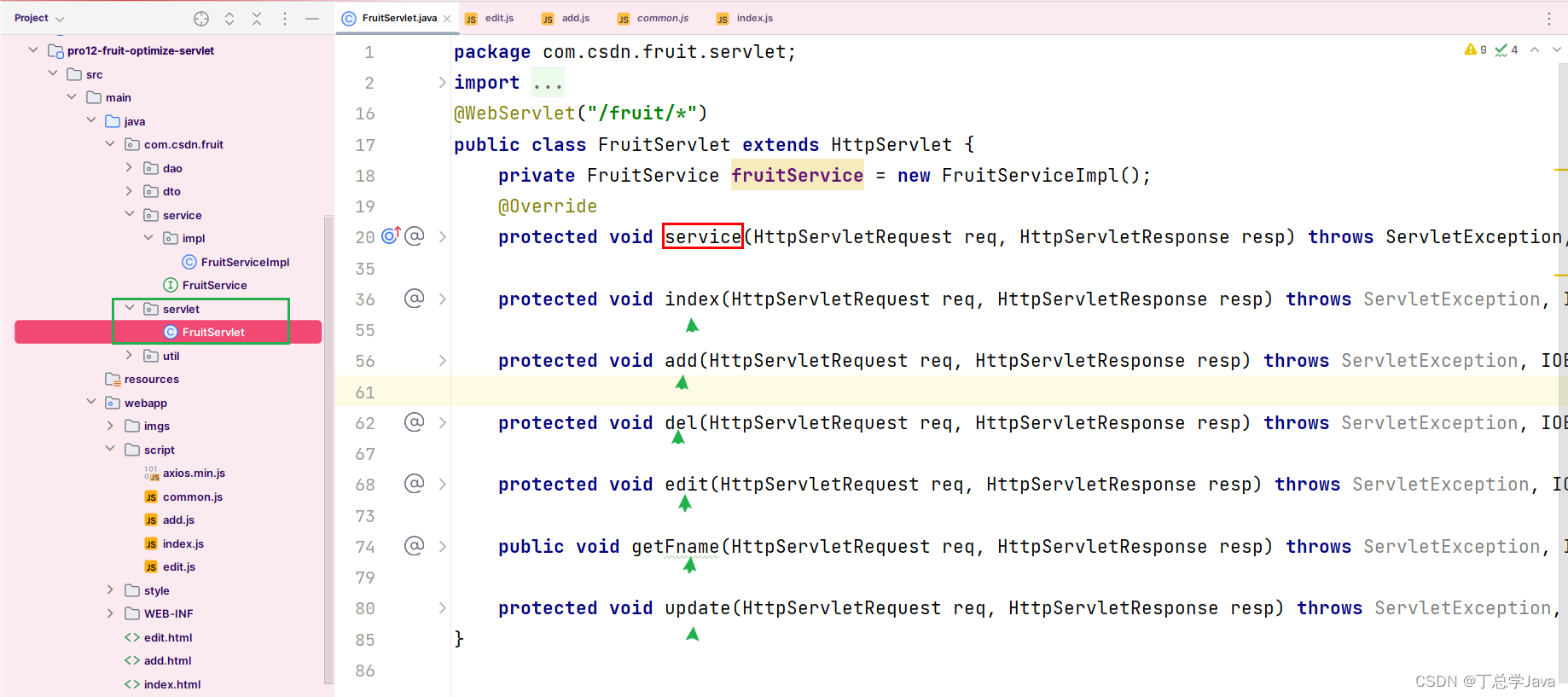
项目实战:优化Servlet,把所有围绕Fruit操作的Servlet封装成一个Servlet
1、FruitServlet 这些Servlet都是围绕着Fruit进行的把所有对水果增删改查的Servlet放到一个Servlet里面,让tomcat实例化一个Servlet对象 package com.csdn.fruit.servlet; import com.csdn.fruit.dto.PageInfo; import com.csdn.fruit.dto.PageQueryParam; import c…...

Go语言函数参数
文章目录 Go语言函数参数1. **函数参数的定义**:2. **参数的数量**:3. **参数的数据类型**:4. **参数的命名**:5. **参数的传递**:6. **参数的传递方式**:7. **空白标识符**: Go语言函数参数 在…...

【遍历二叉树的非递归算法,二叉树的层次遍历】
文章目录 遍历二叉树的非递归算法二叉树的层次遍历 遍历二叉树的非递归算法 先序遍历序列建立二叉树的二叉链表 中序遍历非递归算法 二叉树中序遍历的非递归算法的关键:在中序遍历过某个结点的整个左子树后,如何找到该结点的根以及右子树。 基本思想&a…...
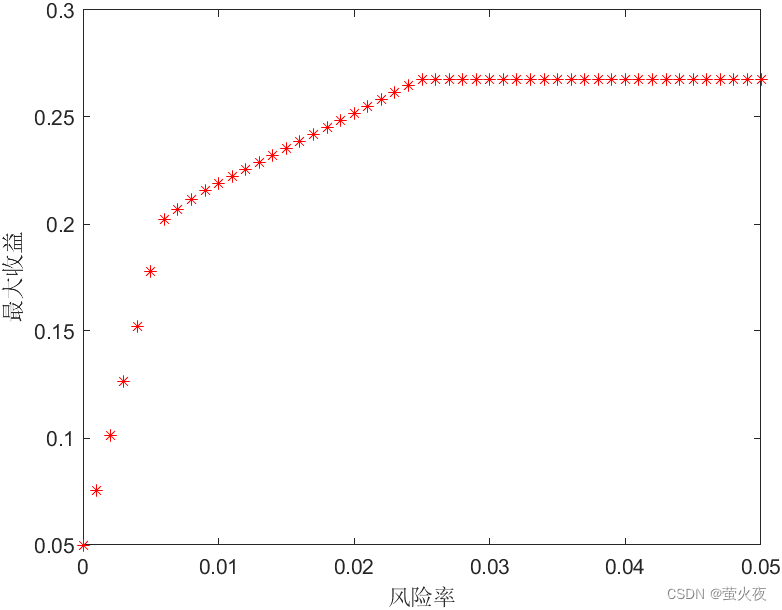
数模之线性规划
线性规划 优化类问题:有限的资源,最大的收益 例子: 华强去水果摊找茬,水果摊上共3个瓜,华强总共有40点体力值,每劈一个瓜能带来40点挑衅值,每挑一个瓜问“你这瓜保熟吗”能带来30点挑衅值,劈瓜消耗20点体力值,问话消耗…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
