数模之线性规划
线性规划
优化类问题:有限的资源,最大的收益
例子:
华强去水果摊找茬,水果摊上共3个瓜,华强总共有40点体力值,每劈一个瓜能带来40点挑衅值,每挑一个瓜问“你这瓜保熟吗”能带来30点挑衅值,劈瓜消耗20点体力值,问话消耗10点体力值, 问如何利用这些瓜,使挑衅值最大?
注意:遇到不懂的词汇去百度搜,去查文献,尽快了解问题背景, 遇到大量陌生专有名词就尽量别选, 例如国赛A题
分析:
注意x1>=0和x2>=0这两个隐藏条件, 可能会对解答有影响
线性规划模型三要素:
线性规划模型:
 题目类型:
题目类型:
题目中提到“XXX有多少多少”“怎样安排/分配”“最多(少)”“利润最大”等词;
生产安排:
原材料、设备有限制,总利润最大
• 若生产两种机床,利润分别为XXX;A机器和B机器加工,有顺序要求,有不同损耗费用,不同的工作时间…;问题:怎样安排生产使得总利润最大?
投资收益:
涉及资产配置、收益率、损失率、组合投资,总收益最大
• 若总资金为M,有n种资产可以配置
• 每种资产的平均收益率…,风险损失率…,手续费…;问题:设计组合投资方案,使得收益尽可能大,总体风险尽可能小(本质是多目标规划,可化简为一个目标的线性规划)
销售运输:
产地、销地、产量、销量、运费,总运费最省
• 商品有m个产地和n个销地,需要从产地运到销地
• 各产地的产量…,各销地需求量…由a产地运到b销地的运价xxx;问题:如何调运才能使总运费最省?
车辆安排:
路线、起点终点、承载量、时间点、车次安排最合理
• 不同种类的车辆有各自的承载量,工地各点之间要安排车辆运输
• 工地里有多条路线……满足用工需求的情况下…;问题:如何安排车辆能使产量尽可能大?注意:最合理这种模糊词需要给出准确的数学定义, 可能是利润最大, 排队时间最短, 运载量最大....
投资类问题的注意事项
• 收益率 = 收益/成本,设收益率为r,收益为g,成本为c
• 如果要求“总收益最大”,一般可以用线性规划
• 如果要求“总收益率最大”,一般是非线性规划, r = g/c, 其中c是-1次方(不绝对)
判断标准
判断的标准就是建立的模型中, 约束条件和目标函数中的变量是否全是一次方
• 如果成本c为变量,追求r最大,目标函数是 max r = g/c,其中变量c的次幂是-1,为非线性
如果成本c始终为常数, 总收益率就变成了线性规划
例题
问题:给该公司设计一种投资组合方案,用给定的资金M,有选择地购买若干种资产或存银行生息,使净收益尽可能大,总体风险尽可能小。
问题分析
有目标函数(净收益尽可能大、总风险尽可能小)
有约束条件(总资金有限,和隐含数学条件:每一笔投资都是非负数)
基本假设
由于投资数额M相当大,而题目设定的定额ui相对M很小,pi*ui更小,因此假设每一笔交易额xi都大于对应的定额ui
模型的建立
决策变量: 投资项目si 的资金为xi (i = 0,1,2,3,4), 总收益Q
目标函数: 净收益尽可能大(max)、总风险尽可能小(min) (所以这是一个多目标线性规划模型)
约束条件: 投资总额为M、每一笔投资非负数
目标函数
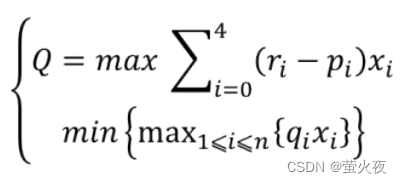
净收益尽可能大(max): 总收益=max(∑每一项的资金×(每一项的收益率-费率))
总风险尽可能小(min): 每一项的资金×风险率的最大值最小
约束条件
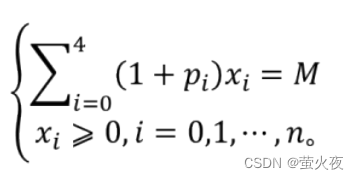
∑每一项的资金和交易费 = 总资金
每一笔投资都是非负数
合理的简化,事半功倍
模型的简化:
现实中,不同人所能承受的风险不同
设某一类投资者,能接受的最大投资风险率为定值a
只要风险率小于等于该定值a,可视为对该类投资者满足“总风险尽可能小”即风险率(风险率=投资额*损失率/总资产)满足:
分情况讨论:设低风险投资者能接受的a=5%,中风险投资者能接受的a=15%等等
基于该简化,将目标函数:
转化为了约束条件:
完成模型的建立
决策变量: xi(i = 0,1,2,3,4), 第i种资产的投资额
目标函数和约束条件:

注意,除了xi(5个变量),其他都是常数
显然,所有变量都是线性的, 因此这是一个(单目标)线性规划模型
模型的建立到求解
建立模型时留下的坑
题目要求“总风险尽可能小”
本模型简化为只要风险率小于等于该定值a, 可视为对某一类投资者满足“总风险尽可能小’·模型中的a是一个常数,而不是变量,所以才能在写代码时套用matlab的函数
求解问题时尽量把坑填上(在论文里写作“模型改进”)
现实中的a是一个变量,不同投资者对风险的接受程度肯定不一样
低风险投资者追求落袋为安, 对应a=5%;高风险投资者追求富贵险中求, 可能对应a=50%·那么在求解时, 对不同a取值分别进行求解(该操作实现了把a作为了“变量”)
代码:
linprog函数使用具体分析:Matlab线性规划函数linprog-小白详解_浩浩的科研笔记的博客-CSDN博客
linprog函数求解线性规划模型, linprog函数中的变量必须是matlab标准型(求最大值转化为求负的最小值, 约束条件是大于变换为小于)
函数:[x,fval]= linprog(f,A,b,Aeq,beq,lb,ub)

% clc是清除命令行窗口,clear是清除存储空间的变量
clc,clear;%a矩阵的元素是不同的风险率,从0到0.05等差取值,相邻的两个数相差0.001
a = (0:0.001:0.05);%目标函数的系数向量,因为求的是M的最大值,所以变为求-M的最小值,系数变为负
f = [-0.05,-0.27,-0.19,-0.185,-0.185]; %A是不等式约束条件的变量系数构成的矩阵
A = [0,0.025,0,0,0;0,0,0.015,0,0;0,0,0,0.055,0;0,0,0,0,0.026];%还可以这样构造A矩阵 A = [zeros(4,1),diag([0.025,0.015,0.055,0.026])]%用zeros先构造4行1列的全是0的矩阵,因为x0没有风险率系数为0%再构造对角矩阵,对角线上的元素为约束条件中的变量x1 x2 x3 x4的系数%等式约束的系数矩阵Aeq = [1 1.01 1.02 1.045 1.065];%M设为1beq = 1;%xi的下界lb = [0;0;0;0;0];%初始化保存最优解的Q矩阵,现在还没求出最优解先初始化为0Q = zeros(1,length(a));%XX用来存不同风险率下的最优解XX = [];for i = 1:length(a)b = a(i)*ones(4,1); %b是约束条件中的常数项矩阵,4行1列,每个元素都是a[x,y] = linprog(f,A,b,Aeq,beq,lb); %x是对应的投资分配xi,是列向量的形式Q(i) = -y; %-y是总收益的最大值XX = [XX;x']; %每次更新XX矩阵,保存每一个a值下的投资分配endplot(a,Q,"*r");
xlabel('风险率'); % x和y轴分别附上标签
ylabel('最大收益');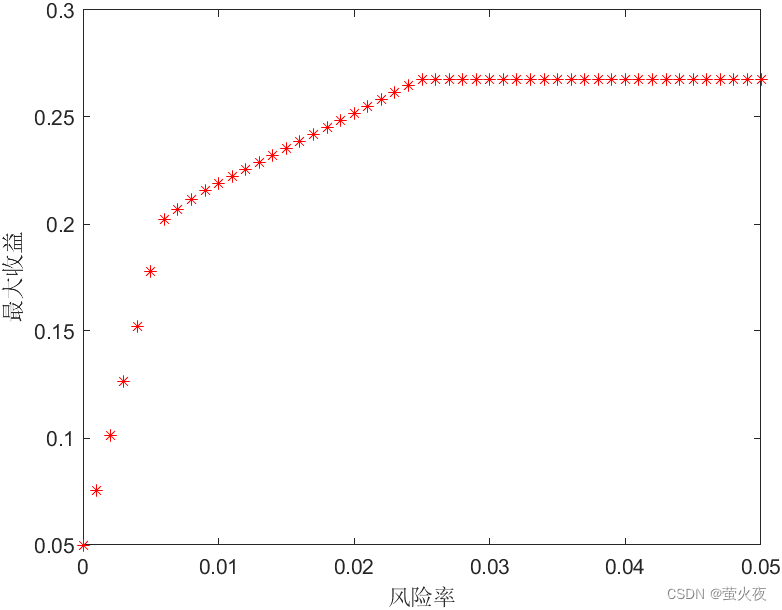
相关文章:

数模之线性规划
线性规划 优化类问题:有限的资源,最大的收益 例子: 华强去水果摊找茬,水果摊上共3个瓜,华强总共有40点体力值,每劈一个瓜能带来40点挑衅值,每挑一个瓜问“你这瓜保熟吗”能带来30点挑衅值,劈瓜消耗20点体力值,问话消耗…...
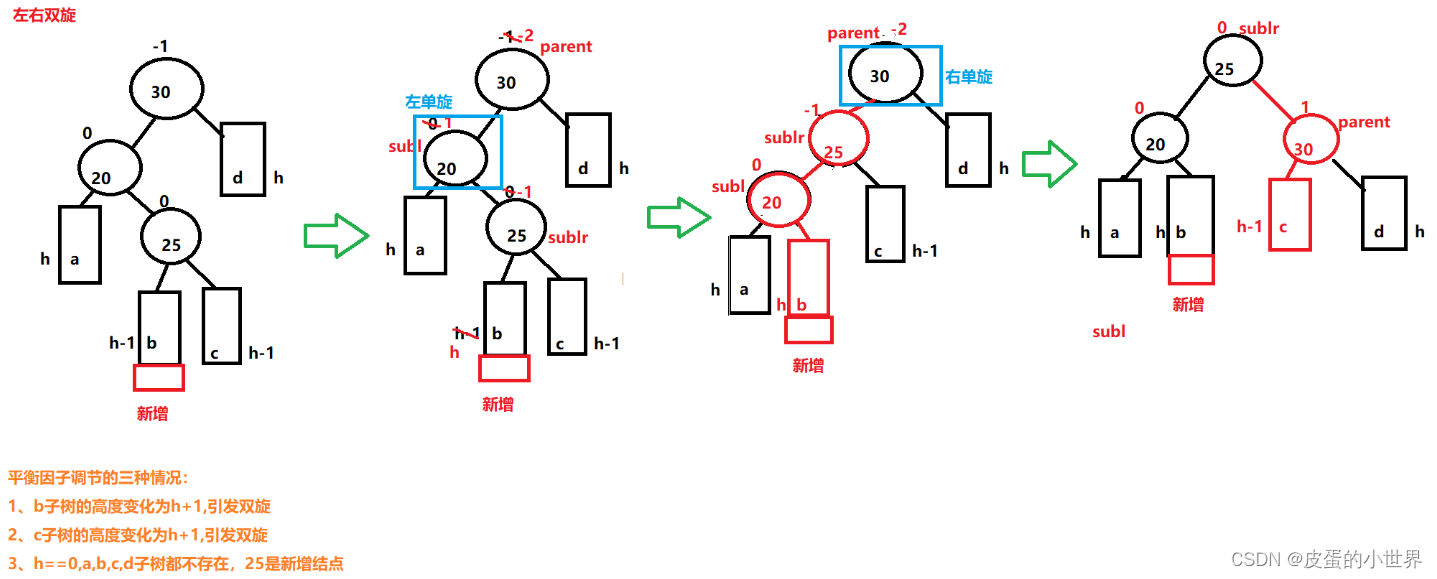
【C++】AVL树的4中旋转调整
文章目录 前提一、AVL树的结构定义二、AVL的插入(重点)1. 插入的结点在较高左子树的左侧(右单旋)2. 新节点插入较高右子树的右侧(左单旋)3.新结点插入较高右子树的左侧(先右单旋再左单旋&#x…...
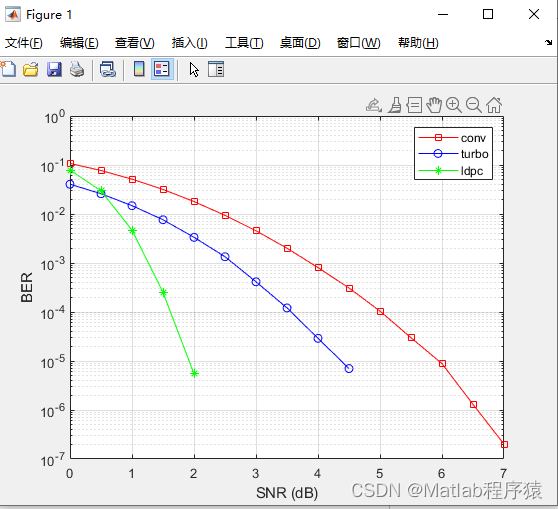
【MATLAB源码-第69期】基于matlab的LDPC码,turbo码,卷积码误码率对比,码率均为1/3,BPSK调制。
操作环境: MATLAB 2022a 1、算法描述 本文章介绍了卷积码、Turbo码和LDPC码。以相同的码率仿真这三种编码,并对比其误码率性能 信源输出的数据符号(二进制)是相互独立和等概率的; 信道是加性白高斯噪声信道&#…...

Java获取时间戳、字符串和Date对象的相互转换、日期时间格式化、获取年月日
获取时间戳(自1970年1月1日经历的毫秒数值) package org.example;import java.util.Date;public class Main {public static void main(String[] args) {Date date1 new Date(1699540662210L);System.out.println(date1.getTime());Date date2 new Dat…...

用c语言实现矩阵转置
下面是在 C 语言中实现矩阵转置的示例代码: #include <stdio.h> #define ROWS 3 #define COLS 3 void transpose(int matrix[ROWS][COLS]) { int temp; for(int i0; i<ROWS; i) { for(int j0; j<i; j) { temp matrix[i][j]; matrix[i][j] matrix[j]…...
)
蓝桥杯官网练习题(移动距离)
题目描述 X 星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为 1,2,3, 当排满一行时,从下一行相邻的楼往反方向排号。 比如:当小区排号宽度为 6 时,开始情形如下: 1 2 3 4 5 6 12 …...
不止于“初见成效”,阿斯利康要让数据流转,以 AI 带动决策智能
“阿斯利康数字化成果在进博会上引人注目,令我感到非常高兴。”这是阿斯利康代表的感慨。 数字化建设目标是利用先进技术来提高企业运营效率,降低成本。在第六届进博会的7.2 B2-01展区,阿斯利康不仅展示了全球领先的生物医药和医疗器械成果&a…...
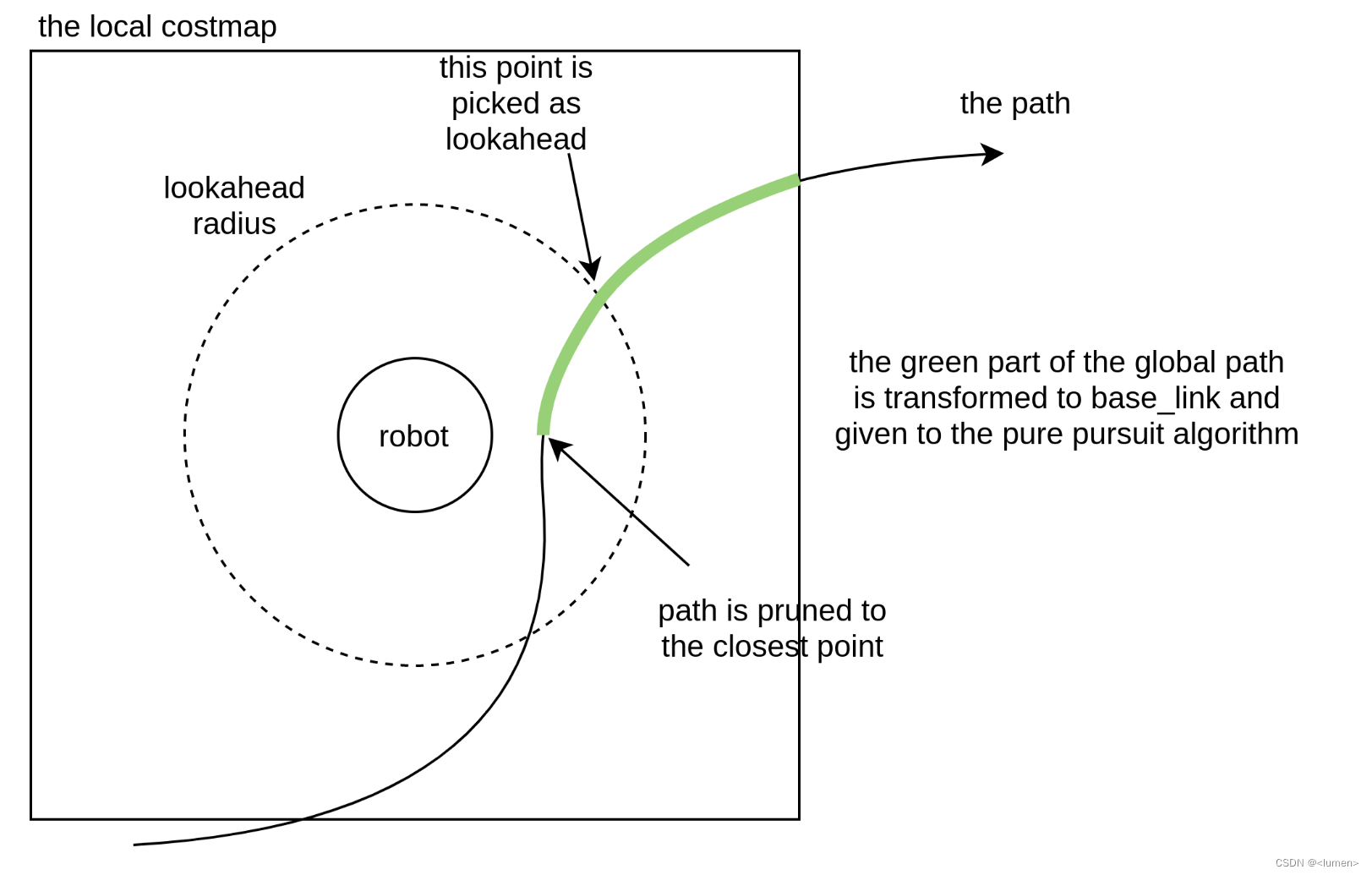
nav2 调节纯追踪算法
纯追踪算法 纯追踪基础 The core idea is to find a point on the path in front of the robot and find the linear and angular velocity to help drive towards it. 核心思想是在机器人前方的路径上找到一个点,并找到一个合适的线速度和角速度,以驱…...
安装RabbitMQ
安装RabbitMQ 下载需要的两个包 # 这直接就可以安装了,下面 ‘上传对应的rmp包’ 操作 [rootrabbitmq-1 ~]# curl -s https://packagecloud.io/install/repositories/rabbitmq/erlang/script.rpm.sh | sudo bash [rootrabbitmq-1 ~]# yum install erlang-21.3.8.2…...
Spring基础(1):两个概念
最近看了点Spring的源码,于是来稍微扯一扯,希望能帮一部分培训班出身的朋友撕开一道口子,透透气。 广义上的Spring指的是Spring整个项目,包含SpringBoot、SpringCloud、SpringFramework、SpringData等等, 本系列文章…...

国产化精密划片机已得到国内更多厂家青睐
国产化精密划片机在近年来得到了国内许多厂家的青睐,这是因为精密划片机在工业生产中有着重要作用。这种设备主要用于高精密切割加工,适用于多种材料,包括硅、石英、氧化铝、氧化铁等。 以精密晶圆划片机为例,这种设备采用了自主研…...

Voice Control for ChatGPT简单高效的与ChatGPT进行交流学习。
快捷又不失灵活性 日常生活中,我们与亲人朋友沟通交流一般都是喜欢语音的形式来完成的,毕竟相对于文字来说语音就不会显的那么的苍白无力,同时最大的好处就是能解放我们的双手吧,能更快实现两者间的对话,沟通便更高效…...

flutter生态一统甜夏 @Android @ios @windowse @macos @linux @Web
(愿景)G o o g l e 中 国flutter生态一统天下(IT) Web Android ios Windowse Macos Linux Google中国https://space.bilibili.com/64169458 https://pub-web.flutter-io.cn 构建 Flutter Web 应用 构建 Flutter Web 应用 - Flutter 中文文档 - Flutter 中文开发者网站 …...

计算机基础知识49
三板斧的使用(views.py) 三个方法:HttpResponse: 返回的是字符串render : 返回html文件redirect : 返回加载HTML页面的 def html(request):print(from html)# return HttpResponse(request) # 它返回的是字符串return render(request,html.html) # 返回html# ret…...
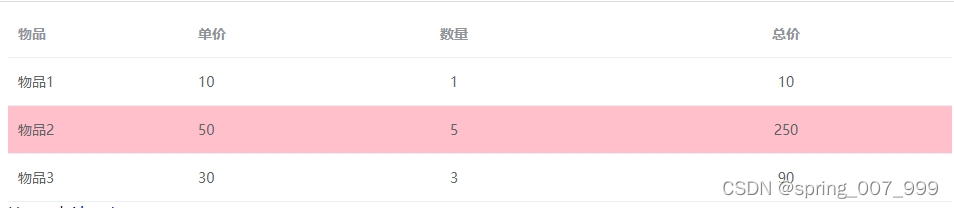
el-table给某一行加背景色
数据列表中总价大于100的一行背景色为红色,效果图如下: 代码示例: <template><div id"app"><!-- 测试区域!!!!!!!!&am…...

搭建 Makefile+OpenOCD+CMSIS-DAP+Vscode arm-none-eabi-gcc 工程模板
STM32F407-GCC-Template Arm-none-eabi-gcc MakefileOpenOCDCMSIS-DAPVscode工程模板 一、本次环境搭建所用的软硬件 1)Windows or Linux (本文以Windows为主) 2)JLink、Daplink、Wch-Link烧录器 3)GNU Arm Embedded Toolchain交叉编译…...
格式的测试)
Unity场景ab包加载压缩(LZ4,LZMA)格式的测试
情况 最近场景越来越大,大概800M的场景加载时间可能长达40秒左右,所以需要测试看看发生了什么。 测试环境 测试环境Win10,21thI5-12600KF,32GRam , Nvidia GF RTX2060 32G Scene1大小:741M 加载代码 首…...
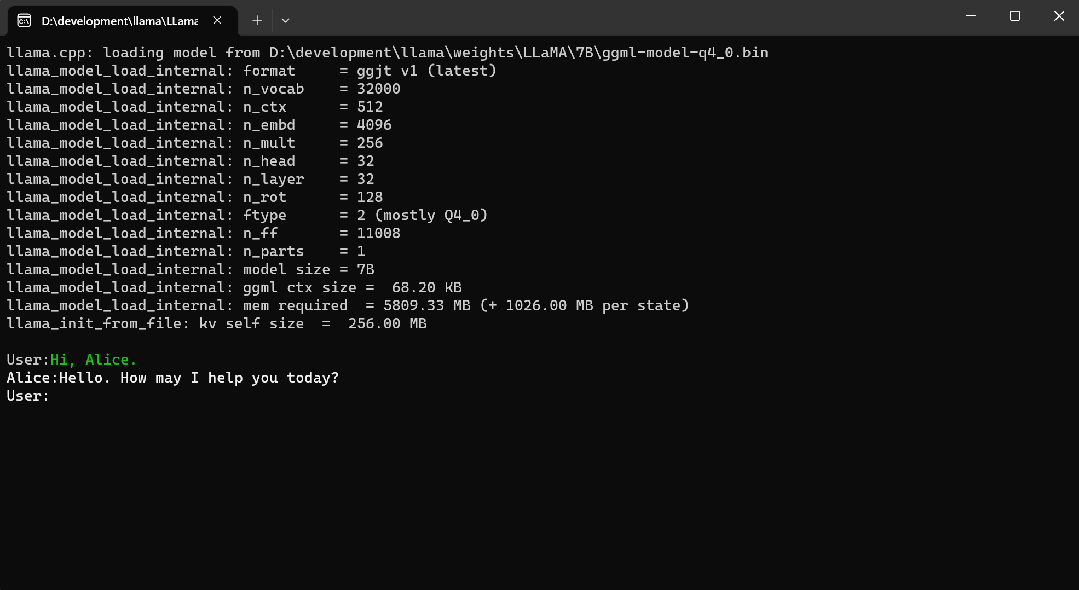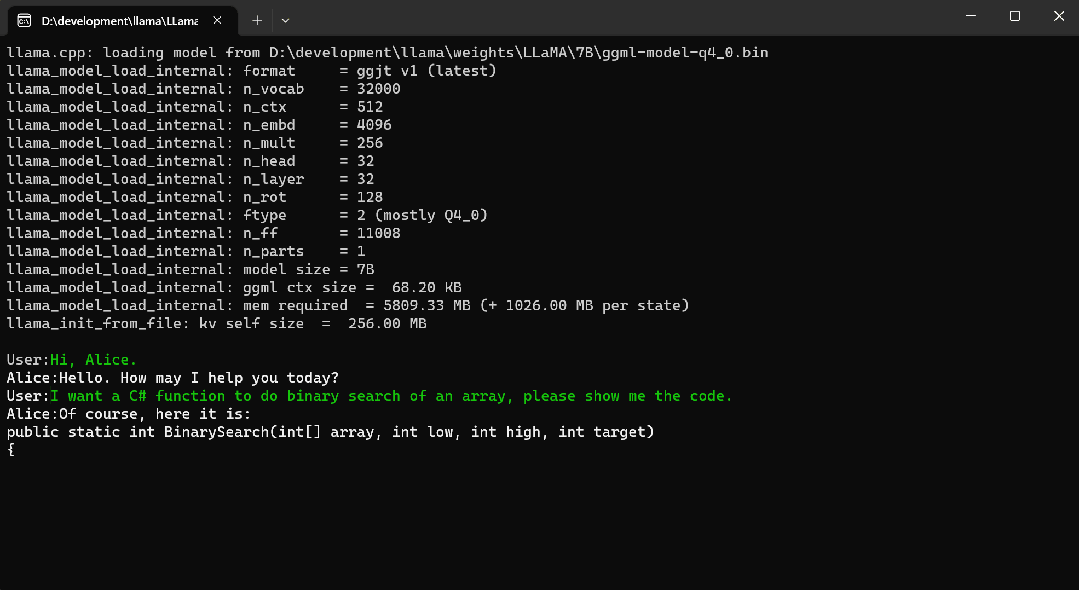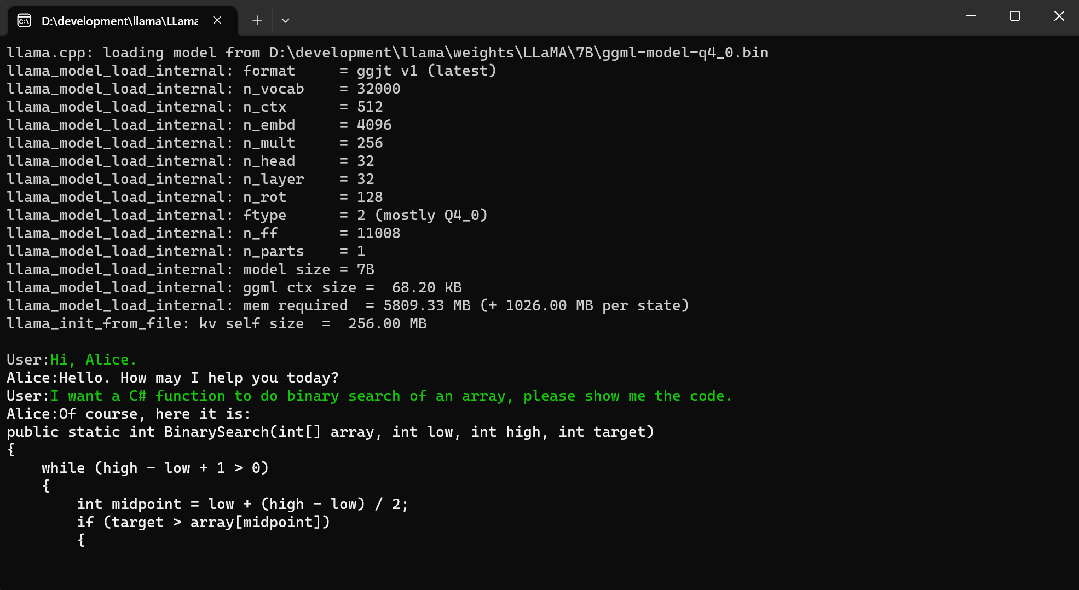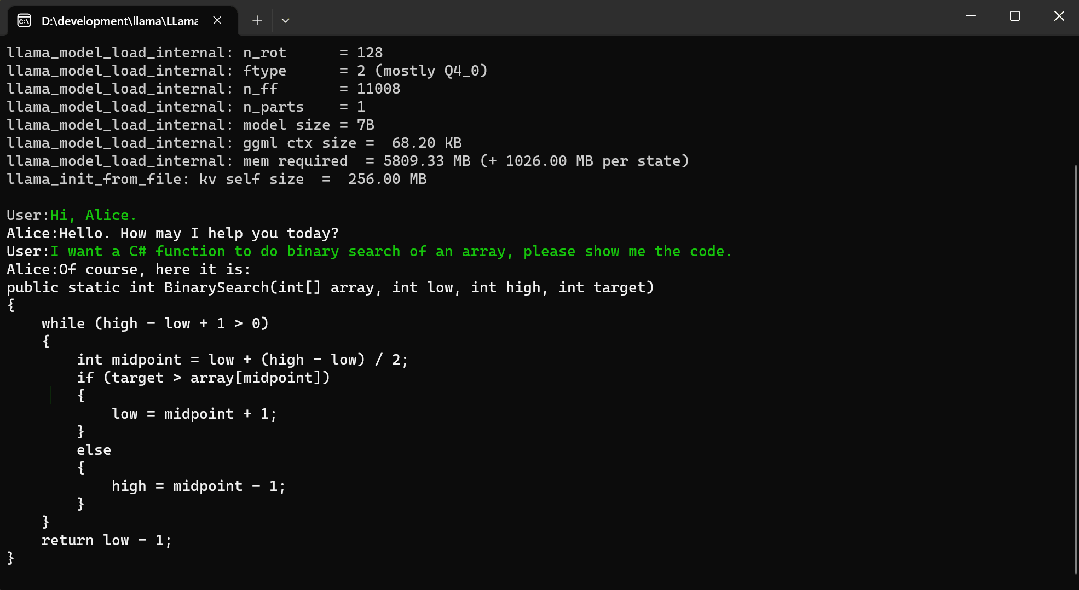
私有化部署大模型:5个.Net开源项目
从零构建.Net前后端分离项目 今天一起盘点下,10月份推荐的5个.Net开源项目(点击标题查看详情)。 1、BootstrapBlazor企业级组件库:前端开发的革新之路 BootstrapBlazor是一个用于构建现代Web应用程序的开源框架,它基…...
安卓系统手机便签app使用哪一款?
在现代快节奏的生活中,我们经常会遇到各种繁忙的事务和容易遗忘的备忘事项。为避免大家遗忘重要的事情,大家可以在常用的手机上安装记录备忘事项的工具,为了帮助安卓用户高效地记录和管理这些信息,今天我将向大家推荐一款功能强大…...
SpringCloud-Gateway无法使用Feign服务(2021.X版本)
Spring Cloud Gateway 2021.x版本,无法使用Feign调用其他服务接口。 问题原因: 在官网的 issue 里面找到了相关的问题。 How to call another micro-service on GatewayFilterFactory ? Issue #1090 spring-cloud/spring-cloud-gateway GitHubHel…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...