区块链技术与应用1——BTC-密码学原理
文章目录
- 比特币中的密码学原理
- 1. 哈希函数
- 2. 数字签名
- 3. 比特币中的哈希函数和数字签名
简单介绍:比特币与以太坊都是以区块链技术为基础的两种加密货币,因为他们应用最广泛,所以讲区块链技术一般就讲比特币和以太坊。
比特币中的密码学原理
1. 哈希函数
– 比特币中哈希函数的性质:
(1)抗碰撞性(collision resistance):
哈希碰撞:
输入:x,y 其中x不等于y
输出:H(x) = H(y)
哈希碰撞一般不可避免,因为输入空间一般远远大于输出空间。
这里的哈希函数的抗碰撞性是指给定一个x,很难(注意是很难,而不是不能)找到一个y(x不等于y),使得H(x)=H(y)
抗碰撞性的意义(用途):用来保证信息完整性,给定一个message,对这个message求哈希值,如果对该message进行了篡改(尽管是很小的修改),那么它的哈希值H(message)就会发生巨大改变。
(2)单向性(隐藏性hiding)
给定一个x,很容易计算出H(x),但给定H(x),却很难计算出x。
达成单向性的前提:输入空间足够大,并且输入空间的分布要相对均匀,使得每种输入取值可能性都基本相等,使得无法通过暴力输入x,来算出给定的H(x)。
实际应用中,如何让输入空间足够大并且输入空间分布相对均匀?
答:通常是在输入x后面添加一个随机数nonce,计算H(x||nonce)
单向性的意义(用途):与抗碰撞性结合可以实现数字等效的密封信封。
a. 将预测结果作为输入x,计算出一个H(x)。
b. 将H(x)保存好,由于H(x)很难计算出x,因此无法提前知道预测结果
c. 当结果出来之后,公布预测结果x,计算H(x)是否和保存好的H(x)相等,由于抗碰撞性,预测结果x很难被篡改,保证了x的完整性。
d. 由此就完成了一个数字等效的密封信封。
(3)谜题友好(puzzle friendly)
哈希值的计算是不可预测的,只看输入x但不计算,很难获得H(x)。即如果你想得到一个H(x)落在某个区间范围内,那么唯一的方法就是一个一个去试x。
比如:想得到一个以k个0开头的的哈希值(00…000xxx…xx),只能去一个一个尝试x来计算H(x)。
– 比特币中使用的哈希函数:
SHA-256
(Secure Hash Algorithm-256)
2. 数字签名
– 比特币中的账户管理:
日常生活中,开户的方法是带证件去银行办理即可,这是中心化的开户方法。比特币是通过去中心化的方法,每个用户开户不需要任何人的批准,他只要在本地生成一个公私钥对(public key, private key)即可。
公钥和私钥是非对称加密体系中的概念。非对称加密是为了解决对称加密中的密钥很难在不安全网络环境下分发而产生的。
公钥可以给任何人看,但私钥要保存好。这样一来在网络上A如果想给B发信息,只需要用B的公钥加密信息,B收到后用私钥解密即可,这样就解决了密钥分发不安全的问题。在比特币中,
公钥相当于你的账户,别人给你转账,只需要你的账户即可。
私钥相当于你的密码,你要取钱或转给别人,那么就需要知道密码才行。但在比特币系统中,是不需要加密的,公钥私钥对的用途在于数字签名。
比如,A转给B十个比特币,因为比特币是去中心化的,这条交易记录需要发布出去给其他人知道才行,于是A发布了这条交易记录,但是别人怎么才能确定的确是A发送了这条记录,而不是别人冒名顶替A把他的比特币转走了呢?这就需要A用自己的私钥对这条交易记录进行签名,然后其他人用A的公钥验证签名,这样就保证了A的身份是真实的。
– 比特币公钥和私钥对生成:
有一种攻击方法:
攻击者通过产生大量的公私钥对,然后用生成的公钥去对比区块链上已有的公钥,如果相同,就用对应的私钥来对交易进行签名,以到达窃取比特币的目的。
但实际上,这种攻击很难达成,因为公私钥对的生成是利用了哈希函数的,由于哈希函数的抗碰撞性,很难计算出一个与已存在公钥相同的公钥。但这个的前提是,有一个很好的随机源(a good source of randomness),如果随机源很差,那就有可能生成两个相同的公钥。
– 比特币中的数字签名:
比特币在数字签名时也要有一个很好的随机源(a good source of randomness),如果随机源不好的话,就有可能泄露私钥。
3. 比特币中的哈希函数和数字签名
比特币中通常是先对一个message进行哈希,然后再对这个哈希值进行数字签名。
相关文章:

区块链技术与应用1——BTC-密码学原理
文章目录比特币中的密码学原理1. 哈希函数2. 数字签名3. 比特币中的哈希函数和数字签名简单介绍:比特币与以太坊都是以区块链技术为基础的两种加密货币,因为他们应用最广泛,所以讲区块链技术一般就讲比特币和以太坊。比特币中的密码学原理 1…...

PyTorch学习笔记:data.WeightedRandomSampler——数据权重概率采样
PyTorch学习笔记:data.WeightedRandomSampler——数据权重概率采样 torch.utils.data.WeightedRandomSampler(weights, num_samples, replacementTrue, generatorNone)功能:按给定的权重(概率)[p0,p1,…,pn−1][p_0,p_1,\dots,p_{n-1}][p0,p1,…,pn…...

SpringMVC对请求参数的处理
如何获取SpringMVC中请求中的信息 ? 默认情况下,可以直接在方法的参数中填写跟请求参数一样的名称,此时会默认接受参 数 ,如果有值,直接赋值,如果没有,那么直接给空值 。Controller RequestMapp…...

12年老外贸的经验分享
回想这12年的经历,很庆幸自己的三观一直是正确的,就是买家第一不管什么原因,只要你想退货,我都可以接受退款。不能退给上级供应商,我就自己留着,就是为了避免因为这个拒收而失去买家。不管是什么质量原因&a…...
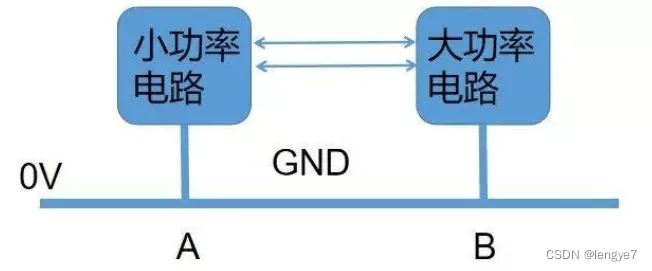
电子电路中的各种接地(接地保护与GND)
前言多年以前,雷雨天气下,建筑会遭遇雷击,从而破坏建筑以及伤害建筑内的人,为了避免雷击的伤害,人们发明了避雷针,并将避雷针接地线,从而引导雷击产生的电流经过地线流入到地下。地线࿱…...

php实现农历公历日期的相互转换
农历(Lunar calendar)和公历(Gregorian calendar)是两种不同的日历系统。公历是基于太阳和地球的运动来计算时间的,而农历是基于月亮的运动来计算时间的。农历中的月份是根据月亮的相对位置来确定的,而公历…...
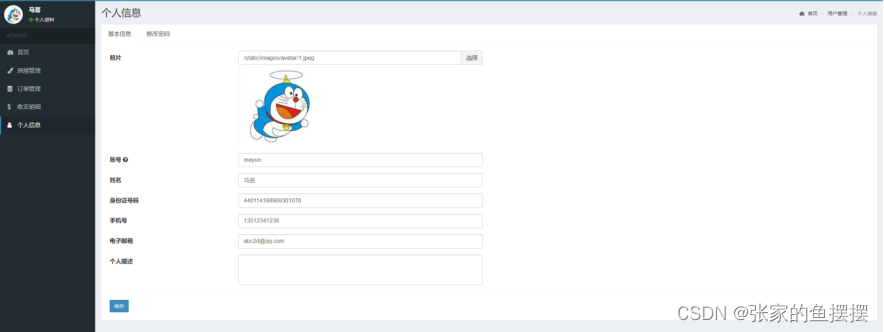
基于SpringBoot的房屋租赁管理系统的设计与实现
基于SpringBoot的房屋租赁管理系统的设计与实现 1 绪论 1.1 课题来源 随着社会的不断发展以及大家生活水平的提高,越来越多的年轻人选择在大城市发展。在大城市发展就意味着要在外面有一处安身的地方。在租房的过程中,大家也面临着各种各样的问题&…...

一文带你为PySide6编译MySQL插件驱动
1.概述 最近使用PySide6开发程序,涉及与MySQL的数据交互。但是qt官方自pyqt5.12(记不太清了)以后不再提供MySQL的插件驱动,只能自己根据qt的源码编译。不过网上大部分都是qt5的MySQL驱动的编译教程。后来搜到了一个qt6的编译教程…...
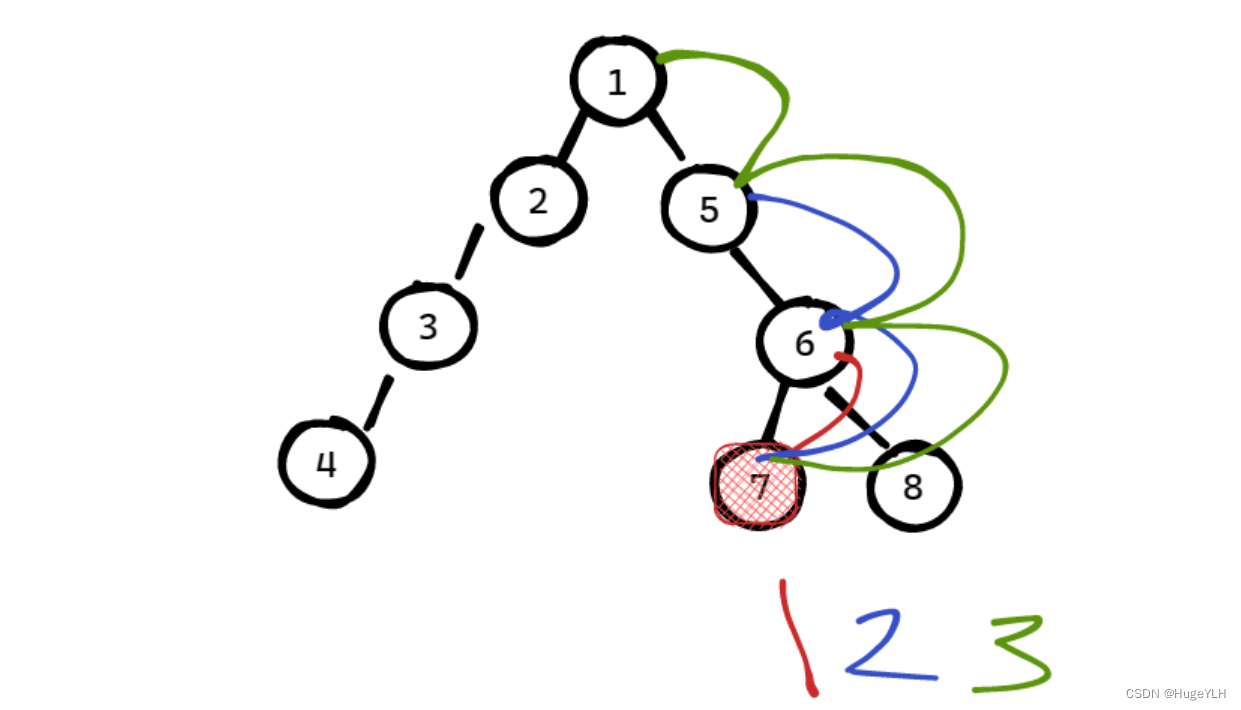
图论算法:树上倍增法解决LCA问题
文章目录树上倍增法: LCA问题树上倍增法: LCA问题 树上倍增法用于求解LCA问题是一种非常有效的方法。 倍增是什么? 简单来说,倍增就是 1 2 4 8 16 … 2^k 可以发现倍增是呈 2的指数型递增的一类数据,和二分一样&…...
 和 execute()方法有什么区别)
Java线程池中submit() 和 execute()方法有什么区别
点个关注,必回关 文章目录一. execute和submit的区别与联系1、测试代码的整体框架如下:2、首先研究Future<?> submit(Runnable task)和void execute(Runnable command),3、submit(Runnable task, T result) 方法可以使submit执行完Run…...

Vue.extend和VueComponent的关系源码解析
目录 0.概念解释 前言 需求分析 Vue.extend 编程式的使用组件 源码分析 0.概念解释 Vue.extend和VueComponent是Vuejs框架中创建组件的两种不同方式。Vue.extend方法能够让你根据Vue对象(继承)来定义一个新的可重用的组件构造器。而VueComponent方…...
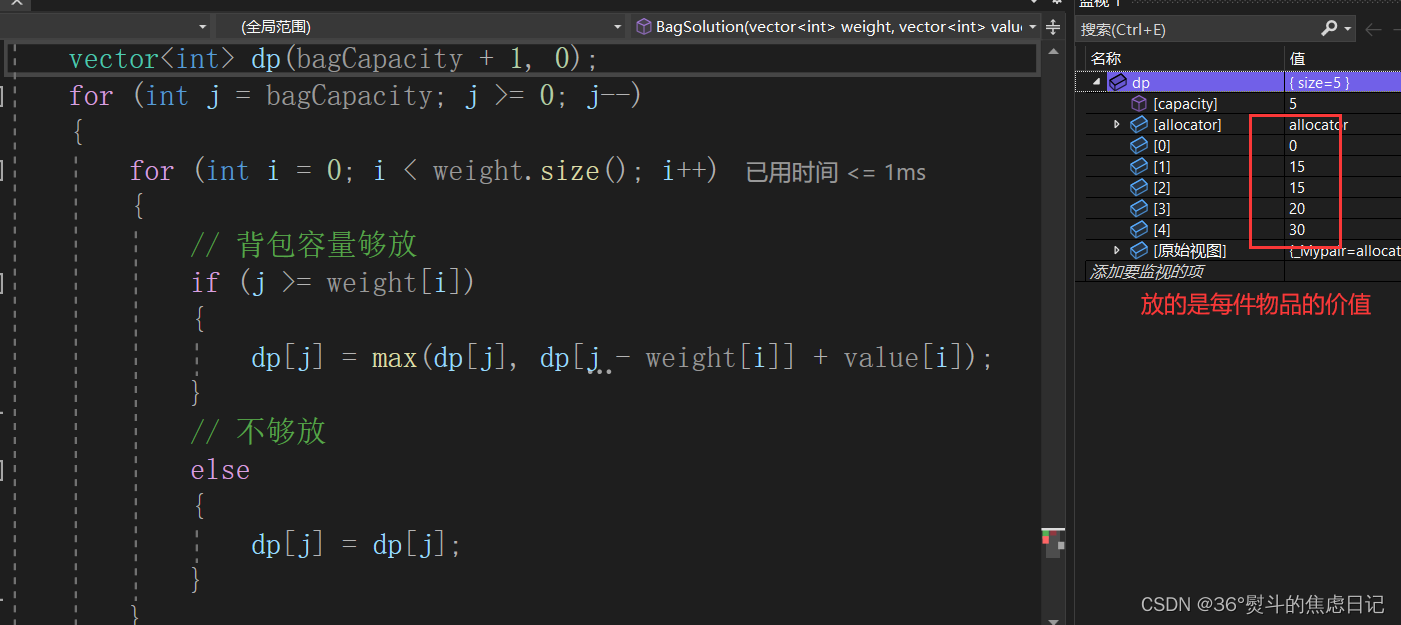
【动态规划】01背包问题(滚动数组 + 手画图解)
01背包除了可以用形象的二维动态数组表示外,还可以使用空间复杂度更低的一维滚动数组。 目录 文章目录 前言 一、滚动数组的基本理解 二、确定dp及其下标含义 三、确定递推公式 四、确定初始化 五、确定遍历顺序 1.用物品(正序)遍历背…...

javaEE 初阶 — 超时重传机制
文章目录超时重传机制1. 数据重复传输问题2. 如何解决数据重复传输问题3. 重传次数问题TCP 的工作机制:确认应答机制 超时重传机制 如果传输数据的时候丢包了该怎么办? 利用 超时重传,也就是超过了一定的时间,如果还没响应就重新…...

小米5x wlan无法打开解决
诱因:想要利用空置设备做节点服务器或者边缘计算,因此解锁并刷了magisk,印象中在刷之前wlan已经无法打开无法进行wifi联网 表现: 1 WLAN开关无法打开,或者虚假打开,无法扫描wifi 2 设置->我的设备->全…...

负载均衡之最小活跃数算法
文章目录[toc]一、概念二、场景与设计思路三、实现四、代码下载一、概念 活跃数 集群中各实例未处理的请求数。 最小活跃数 集群中各个实例,哪个实例未处理的请求数据最小,就称之为最小活跃数。 二、场景与设计思路 场景 以获取微服务地址为场景。 设计…...
JavaScript 评测代码运行速度的几种方法
一、使用 performance.now() API 在 JavaScript 中,可以使用 performance.now() API 来评测代码的运行速度。该 API 返回当前页面的高精度时间戳,您可以在代码执行前后调用它来计算代码执行所需的时间。 例如: let t0 performance.now();…...

Linux 编译器 gcc/g++
本文已收录至《Linux知识与编程》专栏! 作者:ARMCSKGT 演示环境:CentOS 7 目录 前言 正文 gcc/g常用命令 自定义可执行程序名命令-o 预处理指令-E 编译指令-S 汇编指令-c 链接指令gcc 命令巧记口诀 链接库 动态库-动态链接 静态库…...
2.Java基础【Java面试第三季】
2.Java基础【Java面试第三季】前言推荐2.Java基础01_字符串常量Java内部加载-上58同城的java字符串常量池面试code讲解intern()方法---源码解释02_字符串常量Java内部加载-下whyOpenJDK8底层源码说明递推步骤总结考查点03_闲聊力扣算法第一题字节跳动两数求和题目说明面试题解法…...
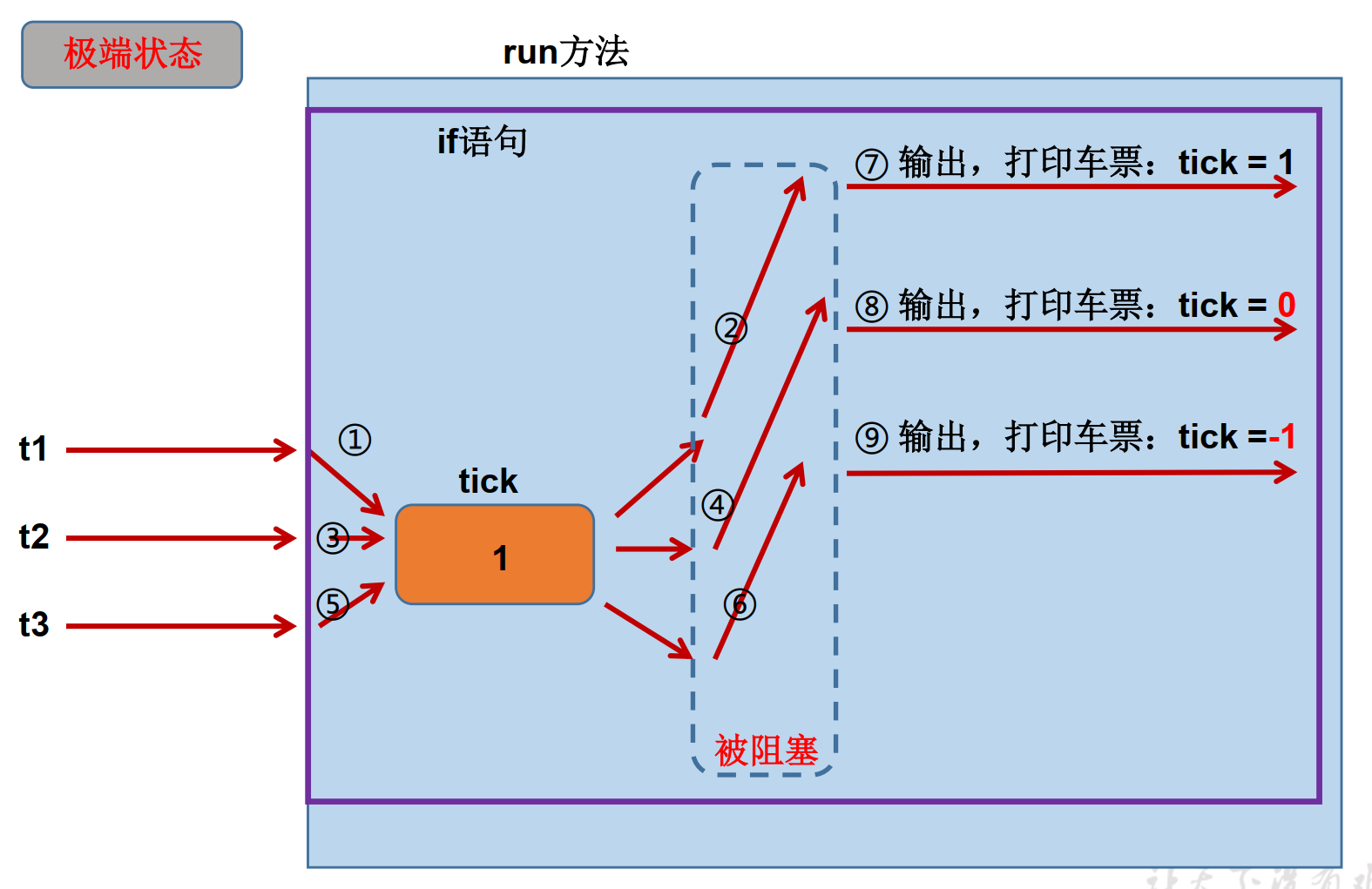
Java高级-多线程
本篇讲解java多线程 基本概念: 程序、进程、线程 **程序(program)**是为完成特定任务、用某种语言编写的一组指令的集合。即指一段静态的代码,静态对象。 **进程(process)**是程序的一次执行过程,或是正在运行的一个程序。是一个动态的过程…...

mysql高级(事务、存储引擎、索引、锁、sql优化、MVCC)
文章目录1.事务1.1 四大特性ACID1.2 并发事务2.存储引擎2.1 InnoDB2.2 MyISAM2.3 Memory2.4 存储引擎特点2.5 存储引擎的选择3.性能分析3.1 查看执行频次3.2 慢查询日志3.3 profile3.4 explain4.索引4.1 索引结构B-TreeBTreeHash面试题4.2 索引分类思考题4.3 语法4.4 使用规则最…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
