空间曲面@常见曲面方程
文章目录
- 曲面的基本问题
- 特殊曲面
- 球面方程
- 球的标准形方程
- 一般形方程
- 例
- 柱面
- 柱面方程
- 不同维度下同方程的图形
- 常见柱面方程
- 旋转曲面
- 旋转曲面的方程
- 旋转情况分类
- 以yOz上的曲线绕 z z z轴旋转为例
- 旋转曲面的方程
- 常见旋转曲面方程
- 锥面
- 其他曲面
曲面的基本问题
- 根据曲面(点的几何轨迹)建立对应的方程
- 例如,更具点法式建立平面方程,就是本类问题
- 根据方程研究对应的曲面形状
特殊曲面
- 最简单的曲面包括:平面和球面
- 在平面一节我们单独地讨论了相关的性质定理和应用
球面方程
- 确定一个球面的要素有两个:
- 球心
- 半径
- 建立球心为 R ( x 0 , y 0 , z 0 ) R(x_0,y_0,z_0) R(x0,y0,z0),半径为R的球方程
- 根据球面上的点和球心距离恒等于半径以及空间两点间距离的计算公式来直观的建立空间直角坐标系内球面方程
- ∣ M M 0 ∣ = ( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 = R |MM_0|=\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}=R ∣MM0∣=(x−x0)2+(y−y0)2+(z−z0)2=R
- 根据球面上的点和球心距离恒等于半径以及空间两点间距离的计算公式来直观的建立空间直角坐标系内球面方程
球的标准形方程
-
( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 = R 2 (x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2 (x−x0)2+(y−y0)2+(z−z0)2=R2,
-
特别的,当球心位于坐标原点 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)方程形式简化为 x 2 + y 2 + z 2 = R 2 x^2+y^2+z^2=R^2 x2+y2+z2=R2
一般形方程
-
x 2 + y 2 + z 2 − 2 ( x 0 x + y 0 y + z 0 z ) + x 0 2 + y 0 2 + z 0 2 − R 2 = 0 x^2+y^2+z^2-2(x_0x+y_0y+z_0z)+x_0^2+y_0^2+z_0^2-R^2=0 x2+y2+z2−2(x0x+y0y+z0z)+x02+y02+z02−R2=0
- 关于 x , y , z x,y,z x,y,z的一次多形式 D ( x , y , z ) = 2 ( x 0 x + y 0 y + z 0 z ) D(x,y,z)=2(x_0x+y_0y+z_0z) D(x,y,z)=2(x0x+y0y+z0z)
- 记常数 E = x 0 2 + y 0 2 + z 0 2 − R 2 E=x_0^2+y_0^2+z_0^2-R^2 E=x02+y02+z02−R2
-
x 2 + y 2 + z 2 + D ( x , y , z ) + E = 0 x^2+y^2+z^2+D (x,y,z)+E=0 x2+y2+z2+D(x,y,z)+E=0
-
将一般式化为标准式时,根据 D ( x , y , z ) D(x,y,z) D(x,y,z)可以直接确定圆心坐标 M 0 ( x 0 , y 0 , z 0 ) M_0(x_0,y_0,z_0) M0(x0,y0,z0),只需要对除以系数 − 2 -2 −2即可
例
- 方程 x 2 + y 2 + z 2 − 2 x + 4 y = 0 x^2+y^2+z^2-2x+4y=0 x2+y2+z2−2x+4y=0
- ( x − 1 ) 2 + ( y − ( − 2 ) ) 2 + z 2 = 1 + 4 + 5 (x-1)^2+(y-(-2))^2+z^2=1+4+5 (x−1)2+(y−(−2))2+z2=1+4+5
- ( x − 1 ) 2 + ( y + 2 ) 2 + z 2 = 5 (x-1)^2+(y+2)^2+z^2=5 (x−1)2+(y+2)2+z2=5
柱面
-
柱面由母线和准线确定,母线是直线,而准线是平面曲线
-
动直线L沿动定曲线C平行移动时所生成的曲面叫作柱面
- 定曲线C叫作柱面的准线
- 曲线C的轨迹可以是不闭合的
- 动直线L叫作柱面的母线
- 直线可以是斜的,而未必是垂直与某个坐标面
- 定曲线C叫作柱面的准线
-
母线决定了柱体的侧面
-
准线决定了主体的地面
-
虽然给定母线和准线,可以唯一确定一个柱面,但给定一个柱面却无法确定唯一的准线,
- 准线可以是非平面曲线,但这些直线沿着母线的投影到坐标面上的曲线是相同的
柱面方程
-
我们主要讨论的是母线平行于坐标轴的柱面,是最简单也是最长见的柱面类型
-
平面曲线的方程仅包含2个字母,例如 x O y xOy xOy上的曲线可以表示为 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0,准线是平面曲线也是主要的研究类型
-
例如,准线 C C C是 x O y xOy xOy坐标面上的曲线,其方程为 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0,而母线平行于 z z z轴的空间柱面方程可以表示为 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0
不同维度下同方程的图形
- 同一个方程在不同维度下表示不同的图形,例如 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0在二维平面上表示一条曲线,而在三维空间中,表示柱面
- 联系:柱面 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0在 x O y xOy xOy平面上的准线 C C C在三维空间中用 f ( x , y ) = 0 ; z = 0 f(x,y)=0;z=0 f(x,y)=0;z=0两个方程表示
常见柱面方程
母线平行于 z z z轴的二次曲面
-
圆柱方程: x 2 + y 2 = R x^2+y^2=R x2+y2=R
-
椭圆柱面方程: x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 a2x2+b2y2=1
-
双曲柱面方程: x 2 a 2 − y 2 b 2 = 1 \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 a2x2−b2y2=1
-
抛物柱面方程: y 2 = 2 p x y^2=2px y2=2px
旋转曲面
- 以一条平面曲线 C C C绕其平面上的一定直线旋转一周所成的曲面称为旋转曲面
- 旋转曲线 C C C称为旋转曲面的母线,定直线称为旋转曲面的轴
旋转曲面的方程
- 平面曲线(绕坐标轴)旋转类曲面的共同特点是可以利用几何关系:曲线上的各点在旋转过程中旋转半径恒定
- 某个点的相对于其旋转轴的距离(旋转半径)的计算可以使用点坐标的距离公式计算
- 为了建立旋转后的点所满足的方程(面由点构成,因此曲面上的点满足的方程也是旋转曲线后构成的曲面的方程)
- 设曲线C若属于某个坐标面,该平面包含的两个坐标轴记为 u 1 , u 2 u_1,u_2 u1,u2,另一个轴是该平面的法线方向,记为 u 0 u_0 u0
- 设已知曲线上的点 M 1 = ( x 1 , y 1 , z 1 ) M_1=(x_1,y_1,z_1) M1=(x1,y1,z1)坐标满足曲线方程 C : f ( u 1 , u 2 ) = 0 C:f(u_1,u_2)=0 C:f(u1,u2)=0(曲线方程仅包含变量 u 1 , u 2 u_1,u_2 u1,u2,因为 u 0 = 0 u_0=0 u0=0在坐标面 u 1 O u 2 u_1Ou_2 u1Ou2上是恒定的)
- 将旋转后的点的坐标记为 M = ( x , y , z ) M=(x,y,z) M=(x,y,z),其中, M M M在旋转轴坐标轴 u 0 u_0 u0上的坐标分量和 M 1 M_1 M1的相同,记为 u 0 ( M ) = u 0 ( M 1 ) u_0(M)=u_0(M_1) u0(M)=u0(M1),其中函数 u 0 ( M ) u_0(M) u0(M)表示计算点 M M M在 u 0 u_0 u0轴上的坐标分量(即投影),可以类似地定义 u 1 ( M ) , u 2 ( M ) u_1(M),u_2(M) u1(M),u2(M)分别表示点M在 u 1 , u 2 u_1,u_2 u1,u2轴上的投影
旋转情况分类
-
绕 u 1 u_1 u1轴旋转
-
曲线C上的点 M 1 M_1 M1在旋转过程中的轨迹所在平面和 u 0 O u 2 u_0Ou_2 u0Ou2平行
-
根据勾股定理,可以确定 M 1 , M M_1,M M1,M在非旋转轴坐标轴上的坐标的关系为:平方和相等,记为 u 0 ( M ) 2 + u 2 ( M ) 2 = u 0 ( M 1 ) 2 + u 2 ( M 1 ) 2 u_0(M)^2+u_2(M)^2=u_0(M_1)^2+u_2(M_1)^2 u0(M)2+u2(M)2=u0(M1)2+u2(M1)2
-
而曲线 C C C属于平面 u 1 O u 2 u_1Ou_2 u1Ou2,从而 u 0 ( M ) 2 + u 2 ( M ) 2 = u 2 ( M 1 ) 2 u_0(M)^2+u_2(M)^2=u_2(M_1)^2 u0(M)2+u2(M)2=u2(M1)2仅根据这个关系,我们还无法得到能够完整描述 M M M的各个坐标分量的关系(方程),需要借助曲线 C C C的方程 C : f ( u 1 , u 2 ) = 0 C:f(u_1,u_2)=0 C:f(u1,u2)=0
- 由于点 M 1 M_1 M1在 C C C上,成立 D : f ( u 1 ( M 1 ) , u 2 ( M 1 ) ) = 0 D:f(u_1(M_1),u_2(M_1))=0 D:f(u1(M1),u2(M1))=0
- u 2 ( M 1 ) = ± u 0 ( M ) 2 + u 2 ( M ) 2 {u_2(M_1)}=\pm\sqrt{u_0(M)^2+u_2(M)^2} u2(M1)=±u0(M)2+u2(M)2
- u 1 ( M ) = u 1 ( M 1 ) u_1(M)=u_1(M_1) u1(M)=u1(M1),即 u 1 ( M 1 ) = u 1 ( M ) u_1(M_1)=u_1(M) u1(M1)=u1(M)
- 方程 D D D,得到 f ( u 1 ( M ) , ± u 0 ( M ) 2 + u 2 ( M ) 2 ) = 0 f(u_1(M),\pm\sqrt{u_0(M)^2+u_2(M)^2})=0 f(u1(M),±u0(M)2+u2(M)2)=0,也就是关于点 M M M的三个坐标分量的关系方程(作为旋转曲面的方程)
-
类似的,可以讨论绕 u 2 u_2 u2轴旋转的情况
以yOz上的曲线绕 z z z轴旋转为例
-
设在 y O z yOz yOz坐标面上有曲线 C : f ( y , z ) = 0 C:f(y,z)=0 C:f(y,z)=0
-
把 C C C绕 z z z轴旋转一周,得到一个以 z z z轴为轴的旋转曲面,它的方程的构造:
-
设 M 1 ( 0 , y 1 , z 1 ) M_1(0,y_1,z_1) M1(0,y1,z1)是曲线 C C C上的一点(位于坐标面 y O z yOz yOz),有 f ( y 1 , z 1 ) = 0 f(y_1,z_1)=0 f(y1,z1)=0成立
-
当 C C C绕 z z z轴旋转时,点 M 1 M_1 M1绕 z z z轴转到另一点 M ( x , y , z ) M(x,y,z) M(x,y,z)
-
此时 z = z 1 z=z_1 z=z1
-
同时点 M M M,到 z z z轴的距离, d = x 2 + y 2 = 0 2 + y 1 2 = ∣ y 1 ∣ d=\sqrt{x^2+y^2}=\sqrt{0^2+y_1^2}=|y_1| d=x2+y2=02+y12=∣y1∣,此时 y 1 = ± d = ± x 2 + y 2 y_1=\pm{d}=\pm{\sqrt{x^2+y^2}} y1=±d=±x2+y2
-
将 z 1 , y 1 z_1,y_1 z1,y1带入到 f ( y 1 , z 1 ) = 0 f(y_1,z_1)=0 f(y1,z1)=0,即 f ( ± x 2 + y 2 , z ) = 0 f(\pm{\sqrt{x^2+y^2}},z)=0 f(±x2+y2,z)=0
-
旋转曲面的方程
- 曲面方程就是描述曲面上所有点的坐标满足的关系式(方程式)
- 因此,我们可以任意取曲面上的某个点 P ( x , y , z ) P(x,y,z) P(x,y,z)进行研究,得到 x , y , z x,y,z x,y,z的方程
- 旋转曲面由其母线和旋转轴唯一确定,因此旋转曲面的方程和母线方程有密切联系
- 我们考虑将旋转曲面上的任意点 P P P和母线上的某点 P 1 P_1 P1联系起来,利用母线上的点满足母线方程的事实来得到曲面方程
- 即,可以通过研究旋转曲面的母线 C C C上的任意一点在旋转过程中形成的轨迹方程来得到旋转曲面的方程
- 以 y O z yOz yOz平面上的曲线 C : f ( y , z ) = 0 C:f(y,z)=0 C:f(y,z)=0绕 z z z轴旋转一周得到的旋转曲面方程求解为例
- 设 P ( x , y , z ) P(x,y,z) P(x,y,z)是旋转曲面 Π \Pi Π上的任意一点,该曲面有 y O z yOz yOz坐标面上的曲线 C C C作为旋转母线绕 z z z轴旋转一周得到的,设 C C C的方程为 f ( y , z ) = 0 f(y,z)=0 f(y,z)=0
- 显然,点 P ( x , y , z ) P(x,y,z) P(x,y,z)可看作是由曲线 C C C上的某点 P 1 P_1 P1旋转得到
- P , P 1 P,P_1 P,P1具有相同的 z z z轴坐标,并且 P 1 P_1 P1是 y O z yOz yOz面(即 x = 0 x=0 x=0平面)上的点,因此 P 1 P_1 P1的 x x x轴坐标为0,因此可设 P 1 ( 0 , y 1 , z ) P_1(0,y_1,z) P1(0,y1,z)
- 另一方面,由旋转关系可知, x 2 + y 2 x^2+y^2 x2+y2= y 1 2 y_1^2 y12,即 y 1 = ± x 2 + y 2 y_1=\pm\sqrt{x^2+y^2} y1=±x2+y2
- 从而 P 1 P_1 P1的坐标分量可以表示为 x , y , z x,y,z x,y,z的式子: P 1 ( 0 , ± x 2 + y 2 , z ) P_1(0,\pm\sqrt{x^2+y^2},z) P1(0,±x2+y2,z),而 P 1 P_1 P1满足曲线 C C C的方程 f ( y , z ) = 0 f(y,z)=0 f(y,z)=0,所以 f ( ± x 2 + y 2 , z ) = 0 f(\pm{\sqrt{x^2+y^2},z})=0 f(±x2+y2,z)=0
(1),此方程描述了旋转曲面上任意点满足的方程,即旋转曲面的方程
- 类似的,若旋转曲面是曲线 C C C绕着 y y y轴旋转,得到的旋转曲面方程为 f ( y , ± x 2 + z 2 ) = 0 f(y,\pm\sqrt{x^2+z^2})=0 f(y,±x2+z2)=0
(2) - 方程(1,2)都包含了 x , y , z x,y,z x,y,z三个变量
常见旋转曲面方程
-
y O z yOz yOz面上抛物线 C : y 2 = 2 p z C:y^2=2pz C:y2=2pz绕 z z z轴旋转所成的曲面方程为 x 2 + y 2 = 2 p z x^2+y^2=2pz x2+y2=2pz,这类曲线称为旋转抛物面
-
y O z yOz yOz面上椭圆线 C : y 2 a 2 + z 2 b 2 = 1 C:\frac{y^2}{a^2}+\frac{z^2}{b^2}=1 C:a2y2+b2z2=1绕 z z z轴旋转所成的曲面方程为 x 2 + y 2 a 2 + z 2 b 2 = 1 \frac{x^2+y^2}{a^2}+\frac{z^2}{b^2}=1 a2x2+y2+b2z2=1,这类曲线称为旋转椭圆面
-
x O z xOz xOz面上双曲线 C : x 2 a 2 − z 2 b 2 = 1 C:\frac{x^2}{a^2}-\frac{z^2}{b^2}=1 C:a2x2−b2z2=1绕 z z z轴, x x x轴旋转所成的曲面方程分别为 x 2 + y 2 a 2 − z 2 b 2 = 1 \frac{x^2+y^2}{a^2}-\frac{z^2}{b^2}=1 a2x2+y2−b2z2=1, x 2 a 2 − y 2 + z 2 b 2 = 1 \frac{x^2}{a^2}-\frac{y^2+z^2}{b^2}=1 a2x2−b2y2+z2=1,这两类曲线分别称为旋转单叶双曲面,旋转双叶双曲面
锥面
- 移动直线 L L L,使它始终通过点 Q Q Q且始终与定曲线 C C C相交,这样由 L L L所生成的曲面叫做锥面
- 特征:顶点与曲面上任意其他点的连线都在曲面上,若顶点在原点,则顶点与锥面上一点 P ( x , y , z ) P(x,y,z) P(x,y,z)的连线直线 L L L方程的参数方程可知, L L L上任意点 T T T可以表示为 ( t x , t y , t z ) (tx,ty,tz) (tx,ty,tz), t t t可以为任意实数
- 因此若 P ( x , y , z ) P(x,y,z) P(x,y,z)满足 f ( x , y , z ) = 0 f(x,y,z)=0 f(x,y,z)=0,则 T ( t x , t y , t z ) T(tx,ty,tz) T(tx,ty,tz)也满足 f ( x , y , z ) = 0 f(x,y,z)=0 f(x,y,z)=0
其他曲面
- 一般的,对于给定的曲面方程,可以考察:
- 对称性
- 图形范围
- 描绘一般曲线方程的图形通常比较困难,但是可以用一组平面取截曲面,得到一组交线(截痕),可以获得大体的曲面形状
- 常用截面为简单平面方程,例如 z = z 0 z=z_0 z=z0
相关文章:

空间曲面@常见曲面方程
文章目录 曲面的基本问题特殊曲面球面方程球的标准形方程一般形方程例 柱面柱面方程不同维度下同方程的图形常见柱面方程 旋转曲面旋转曲面的方程旋转情况分类以yOz上的曲线绕 z z z轴旋转为例 旋转曲面的方程常见旋转曲面方程 锥面其他曲面 曲面的基本问题 根据曲面(点的几何…...

unity 接收和发送Udp消息
因为需要用到unity和其他的程序交互,其他程序可以提供Udp消息,因此找了合适的相互连接方法。这里直接上代码。 工具类: using System; using System.Collections; using System.Collections.Generic; using System.IO; using System.Net; u…...

机器学习股票大数据量化分析与预测系统 - python 计算机竞赛
文章目录 0 前言1 课题背景2 实现效果UI界面设计web预测界面RSRS选股界面 3 软件架构4 工具介绍Flask框架MySQL数据库LSTM 5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 机器学习股票大数据量化分析与预测系统 该项目较为新颖&am…...
)
架构描述语言(ADL)
1.架构描述语言(ADL) 架构描述语言(Architecture Description Language, ADL)是一种为明确说明软件系统的概念架构和对这些概念架构建模提供功能的语言。 2.ADL基本构成要素 ADL即架构描述语言,其基本构成要素包括:…...
GZ038 物联网应用开发赛题第2套
2023年全国职业院校技能大赛 高职组 物联网应用开发 任 务 书 (第2套卷) 工位号:______________ 第一部分 竞赛须知 一、竞赛要求 1、正确使用工具,操作安全规范; 2、竞赛过程中如有异议,可向现场考评人员反映,不得扰乱赛场秩序; 3、遵守赛场纪律,尊重考评人员,…...
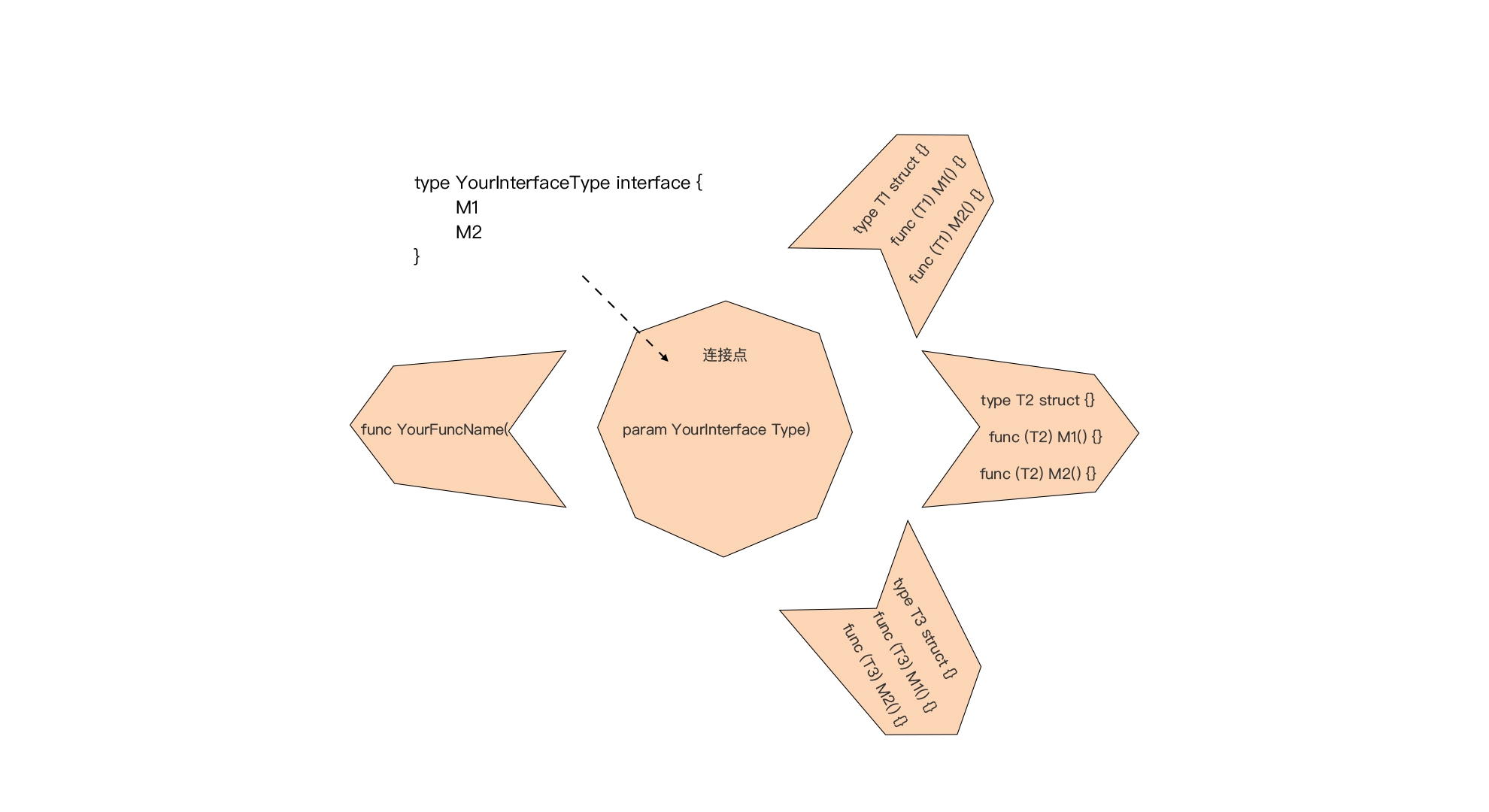
Go 接口:Go中最强大的魔法,接口应用模式或惯例介绍
Go 接口:Go中最强大的魔法,接口应用模式或惯例介绍 文章目录 Go 接口:Go中最强大的魔法,接口应用模式或惯例介绍一、前置原则二、一切皆组合2.1 一切皆组合2.2 垂直组合2.2.1 第一种:通过嵌入接口构建接口2.2.2 第二种:通过嵌入接…...
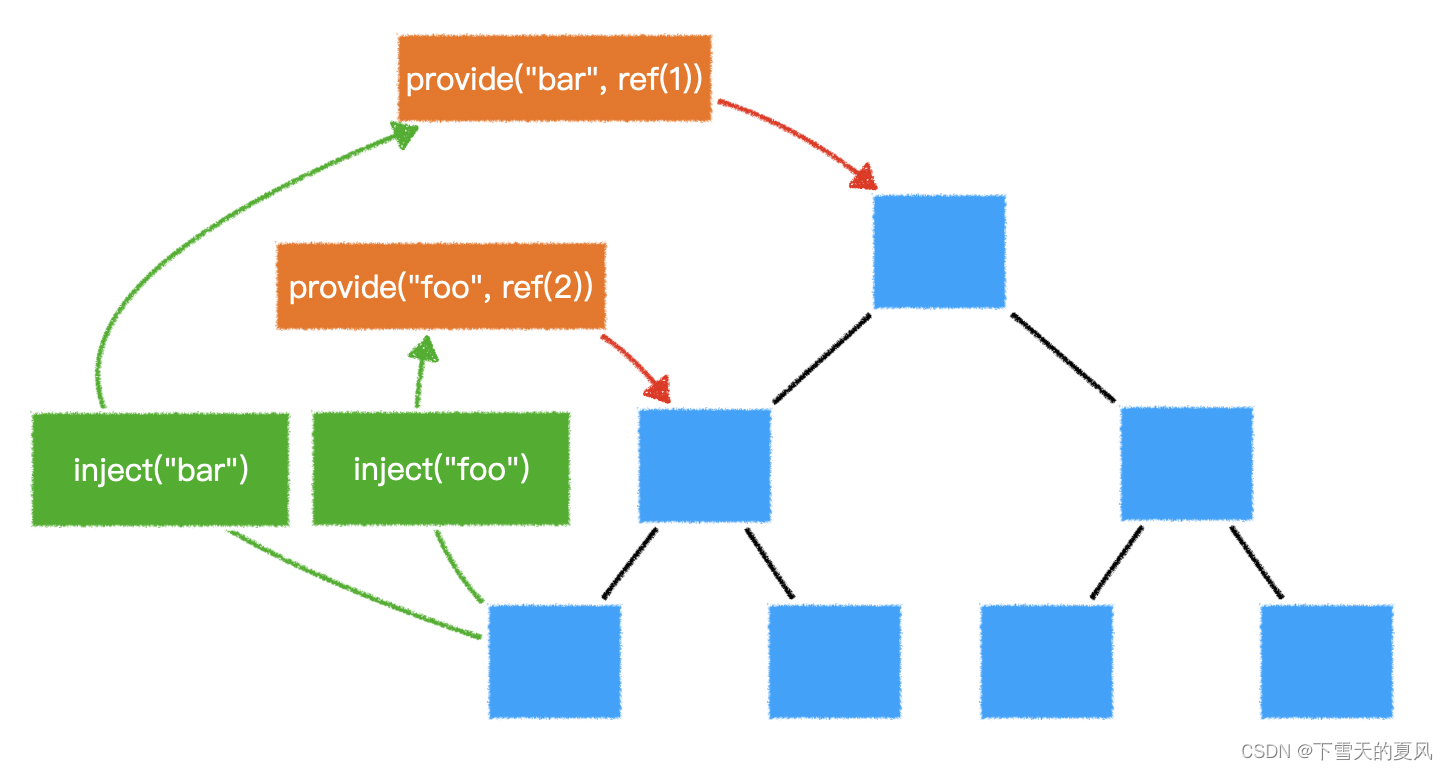
Vue3全局共享数据
目录 1,Vuex2,provide & inject2,global state4,Pinia5,对比 1,Vuex vue2 的官方状态管理器,vue3 也是可以用的,需要使用 4.x 版本。 相对于 vuex3.x,有两个重要变…...
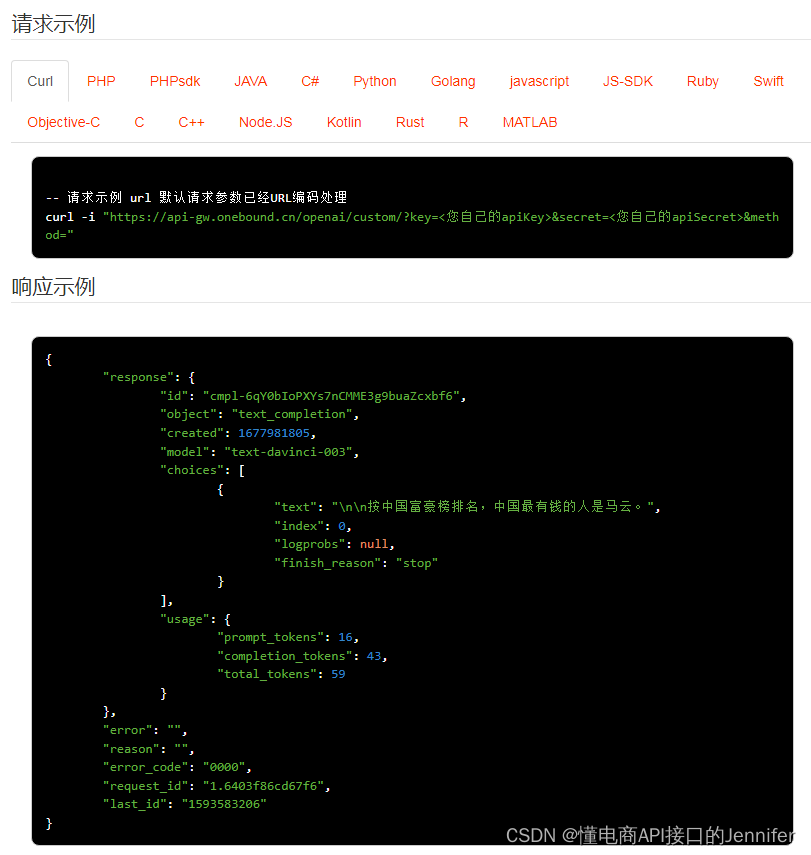
openai自定义API操作 API 返回值说明
custom-自定义API操作 openai.custom 公共参数 名称类型必须描述keyString是调用key(获取测试key)secretString是调用密钥api_nameString是API接口名称(包括在请求地址中)[item_search,item_get,item_search_shop等]cacheStrin…...

jsp基本表格和简单算法表格
基本表格; <% page language"java" contentType"text/html; charsetUTF-8"pageEncoding"UTF-8"%><!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd…...

在线存储系统源码 网盘网站源码 云盘系统源码
Cloudreve云盘系统源码-支持本地储存和对象储存,界面美观 云盘系统安装教程 测试环境:PHP7.1 MYSQL5.6 Apache 上传源码到根目录 安装程序: 浏览器数据 http://localhost/CloudreveInstallerlocalhost更换成你的网址 安装完毕 记住系统默认的账号密码 温馨提示:如果默认…...
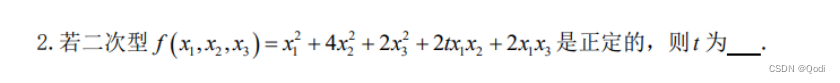
线性代数(六)| 二次型 标准型转换 正定二次型 正定矩阵
文章目录 1. 二次型化为标准型1.1 正交变换法1.2 配方法 2 . 正定二次型与正定矩阵 1. 二次型化为标准型 和第五章有什么样的联系 首先上一章我们说过对于对称矩阵,一定存在一个正交矩阵Q,使得$Q^{-1}AQB $ B为对角矩阵 那么这一章中,我们…...
Kotlin系列之注解详解
目录 注解:file:JvmName 注解:JvmField 注解:JvmOverloads 注解:JvmStatic 注解:JvmMultifileClass 注解:JvmSynthetic 注解:file:JvmName file:JvmName(“XXX”) 放在类的最顶层&#x…...
Go 面向对象,多态,基本数据类型
程序功能解读 第一行为可执行程序的包名,所有的Go源文件头部必须有一个包生命语句,Go通过包名来管理命名空间。 第三行import是引用外部包的说明 func关键字声明定义一个函数,如果是main则代表是Go程序入口函数 Go源码特征解读 源程序以.g…...

使用 Python修改JSON 文件中对应键值
文章目录 前言代码分析 前言 在日常的数据处理工作中,经常需要对 JSON 文件进行读取和修改。在 Python 中,处理 JSON 文件非常方便。本文将通过一个简单的示例程序来演示如何读取和修改 JSON 文件。 代码分析 首先,需要导入 json 和 os 模块…...
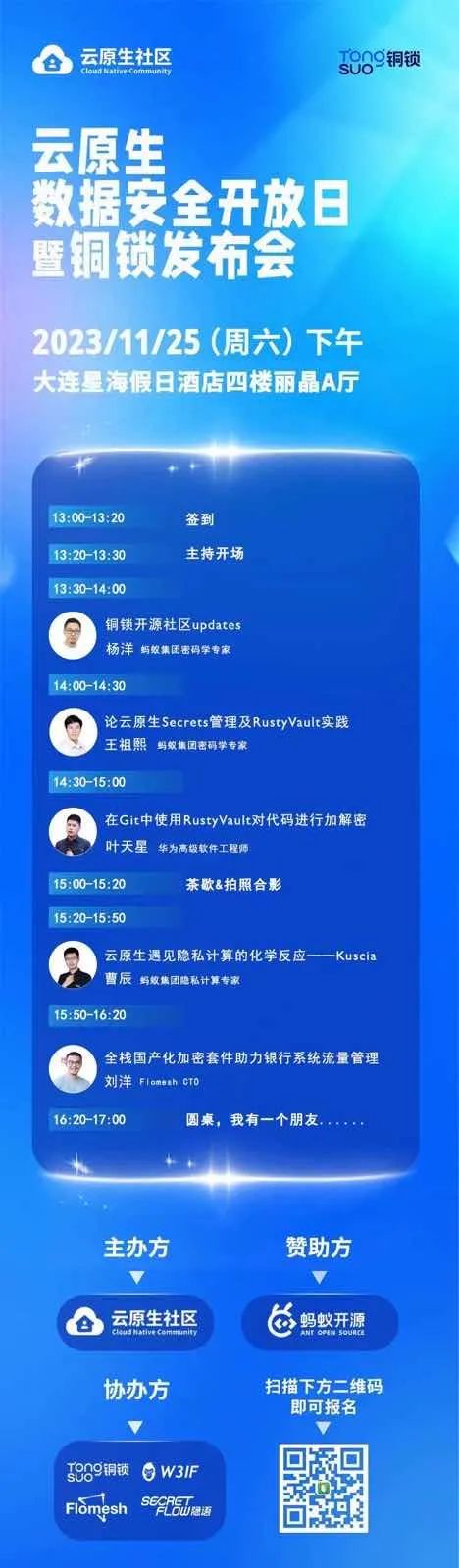
【Rust日报】2023-11-08 RustyVault -- 基于 rust 的现代秘密管理系统
RustyVault -- 基于 rust 的现代秘密管理系统 RustyVault 是一个用 Rust 编写的现代秘密管理系统。RustyVault 提供多种功能,支持多种场景,包括安全存储、云身份管理、秘密管理、Kubernetes 集成、PKI 基础设施、密码计算、传统密钥管理等。RustyVault 可…...
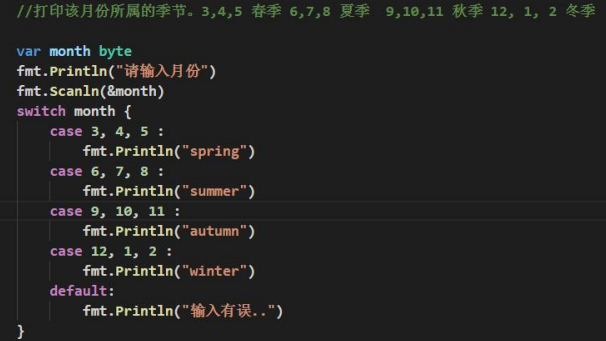
07【保姆级】-GO语言的程序流程控制【if switch for while 】
之前我学过C、Java、Python语言时总结的经验: 先建立整体框架,然后再去抠细节。先Know how,然后know why。先做出来,然后再去一点点研究,才会事半功倍。适当的囫囵吞枣。因为死抠某个知识点很浪费时间的。对于GO语言&a…...

求2个字符串的最短编辑距离 java 实现
EditStepInfo.java: import lombok.Getter; import lombok.Setter;import java.io.Serializable; import java.util.List;Getter Setter public class EditStepInfo implements Serializable {private String str1;private String str2;// str1和 str2 的最短编辑路…...
单例模式 rust和java的实现
文章目录 单例模式介绍应用实例:优点使用场景 架构图JAVA 实现单例模式的几种实现方式 rust实现 rust代码仓库 单例模式 单例模式(Singleton Pattern)是最简单的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创建…...
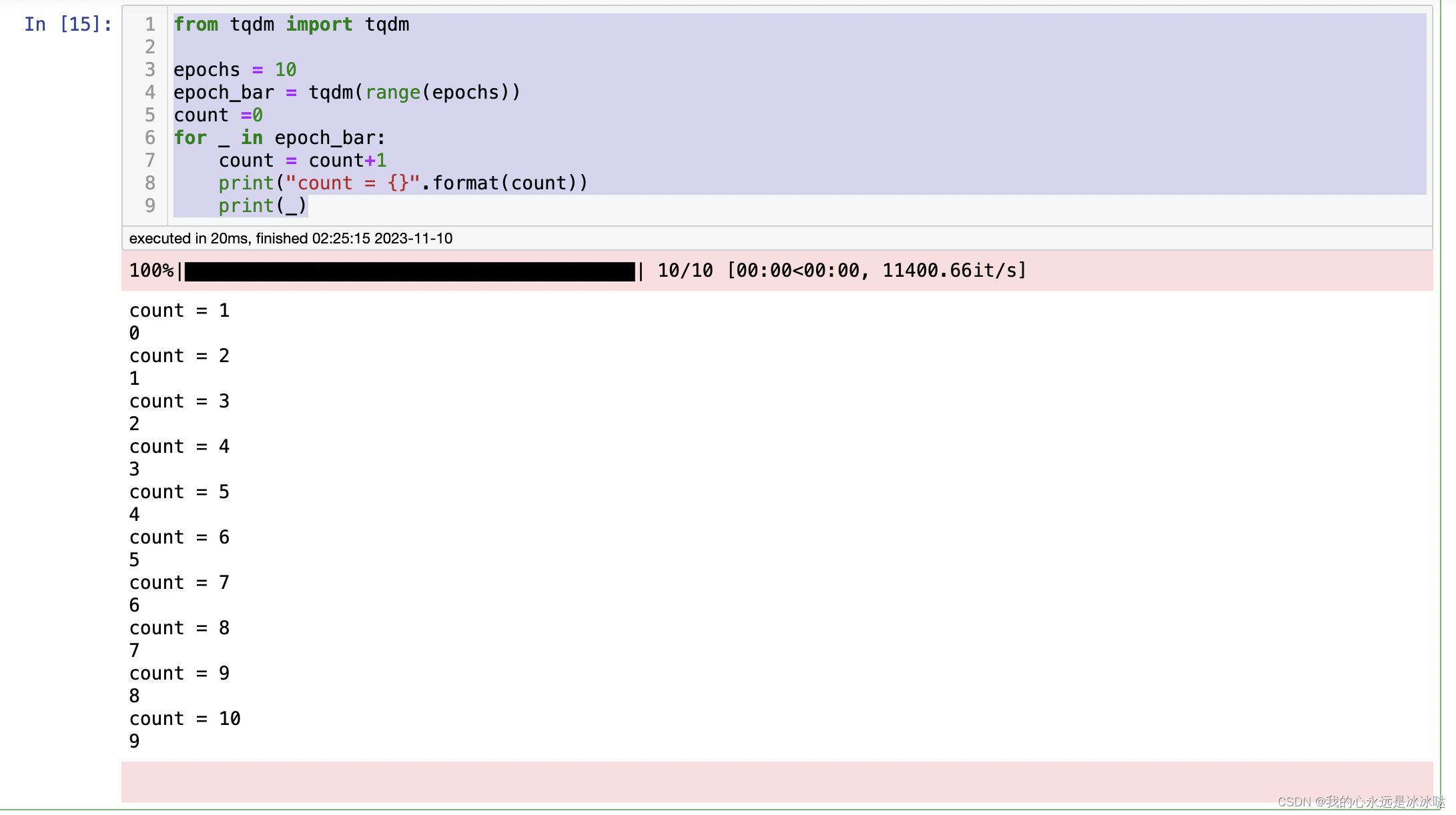
tqdm学习
from tqdm import tqdmepochs 10 epoch_bar tqdm(range(epochs)) count 0 for _ in epoch_bar:count count1print("count {}".format(count))print(_)每次就是一个epoch...

Zigbee—网络层地址分配机制
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:孤雏 0:21━━━━━━️💟──────── 4:14 🔄 ◀️ ⏸ ▶️ ☰ 💗关注…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
