flink的AggregateFunction,merge方法作用范围
背景
AggregateFunction接口是我们经常用的窗口聚合函数,其中有一个merge方法,我们一般情况下也是实现了的,但是你知道吗,其实这个方法只有在你使用会话窗口需要进行窗口合并的时候才需要实现
AggregateFunction.merge方法调用时机
AggregateFunction.merge方法其实只有在使用会话窗口进行窗口合并的时候才会用到,如下所示

对应的源码首先查看WindowOperator.processElement方法对要合并的窗口的状态进行合并
public void processElement(StreamRecord<IN> element) throws Exception {final Collection<W> elementWindows =windowAssigner.assignWindows(element.getValue(), element.getTimestamp(), windowAssignerContext);// if element is handled by none of assigned elementWindowsboolean isSkippedElement = true;final K key = this.<K>getKeyedStateBackend().getCurrentKey();if (windowAssigner instanceof MergingWindowAssigner) {MergingWindowSet<W> mergingWindows = getMergingWindowSet();for (W window : elementWindows) {// adding the new window might result in a merge, in that case the actualWindow// is the merged window and we work with that. If we don't merge then// actualWindow == windowW actualWindow =mergingWindows.addWindow(window,new MergingWindowSet.MergeFunction<W>() {@Overridepublic void merge(W mergeResult,Collection<W> mergedWindows,W stateWindowResult,Collection<W> mergedStateWindows)throws Exception {triggerContext.key = key;triggerContext.window = mergeResult;triggerContext.onMerge(mergedWindows);for (W m : mergedWindows) {triggerContext.window = m;triggerContext.clear();deleteCleanupTimer(m);}// 合并窗口的状态windowMergingState.mergeNamespaces(stateWindowResult, mergedStateWindows);}});
继续查看AbstractHeapMergingState.mergeNamespaces方法,
public void mergeNamespaces(N target, Collection<N> sources) throws Exception {if (sources == null || sources.isEmpty()) {return; // nothing to do}final StateTable<K, N, SV> map = stateTable;SV merged = null;// merge the sourcesfor (N source : sources) {// get and remove the next source per namespace/keySV sourceState = map.removeAndGetOld(source);if (merged != null && sourceState != null) {//此处合并状态并调用AggregateFunction.merge方法merged = mergeState(merged, sourceState);} else if (merged == null) {merged = sourceState;}}// merge into the target, if neededif (merged != null) {map.transform(target, merged, mergeTransformation);}
}//真正调用AggregateFunction.merge方法合并自定义的状态
@Override
protected ACC mergeState(ACC a, ACC b) {return aggregateTransformation.aggFunction.merge(a, b);
}
这样AggregateFunction.merge的调用过程就清楚了,实际应用中,我们只需要在使用会话窗口时才需要实现这个方法,其他的基于时间窗口的方式不需要实现这个方法,当然实现了也不会有错
相关文章:

flink的AggregateFunction,merge方法作用范围
背景 AggregateFunction接口是我们经常用的窗口聚合函数,其中有一个merge方法,我们一般情况下也是实现了的,但是你知道吗,其实这个方法只有在你使用会话窗口需要进行窗口合并的时候才需要实现 AggregateFunction.merge方法调用时…...
Day25力扣打卡
打卡记录 寻找旋转排序数组中的最小值(二分) 链接 由于是旋转排序数组,所以整个数组有两部分是递增的,选取右侧最后元素,即可将整个数组分为大于该元素和小于该元素,碰头地段即为最小值。 class Solutio…...

SpringCloud - OpenFeign 参数传递和响应处理(全网最详细)
目录 一、OpenFeign 参数传递和响应处理 1.1、feign 客户端参数传递 1.1.1、零散类型参数传递 1. 例如 querystring 方式传参 2. 例如路径方式传参 1.1.2、对象参数传递 1. 对象参数传递案例 1.1.3、数组参数传递 1. 数组传参案例 1.1.4、集合类型的参数传递…...

Postgresql数据类型-布尔类型
前面介绍了PostgreSQL支持的数字类型、字符类型、时间日期类型,这些数据类型是关系型数据库的常规数据类型,此外PostgreSQL还支持很多非常规数据类型,比如布尔类型、网络地址类型、数组类型、范围类型、json/jsonb类型等,从这一节…...

SPASS-交叉表分析
导入数据 修改变量测量类型 分析->描述统计->交叉表 表中显示行、列变量通过卡方检验给出的独立性检验结果。共使用了三种检验方法。上表各种检验方法显著水平sig.都远远小于0.05,所以有理由拒绝实验准备与评价结果是独立的假设,即认为实验准备这个评价指标是…...

用Python的requests库来模拟爬取地图商铺信息
由于谷歌地图抓取商铺信息涉及到API使用和反爬虫策略,直接爬取可能会遇到限制。但是,我们可以使用Python的requests库来模拟爬取某个网页,然后通过正则表达式或其他文本处理方法来提取商铺信息。以下是一个简单的示例: # 导入requ…...

使用EvoMap/Three.js模拟无人机灯光秀
一、创建地图对象 首先我们需要创建一个EM.Map对象,该对象代表了一个地图实例,并设置id为"map"的文档元素作为地图的容器。 let map new EM.Map("map",{zoom:22.14,center:[8.02528, -29.27638, 0],pitch:71.507,roll:2.01,maxPit…...
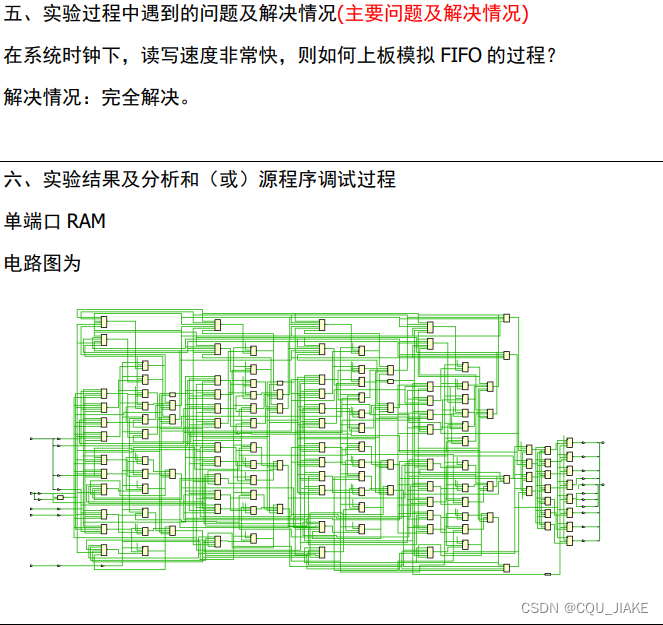
11.9存储器实验总结(单ram,双ram,FIFO)
实验设计 单端口RAM实现 双端口RAM实现 FIFO实现 文件结构为...
安装并使用scrcpy)
linux(ubuntu)安装并使用scrcpy
scrcpy 是一款开源的在计算机上显示和控制 Android 设备的工具。要在 Ubuntu 上使用 scrcpy,你可以按照以下步骤进行安装: 通过命令行安装 scrcpy: 安装 scrcpy: 打开终端(Terminal)并执行以下命令来安装…...

linux rsyslog安装配置
syslog是Linux系统默认的日志守护进程。默认的syslog配置文件是/etc/rsyslog.conf文件。syslog守护进程是可配置的,它允许人们为每一种类型的系统信息精确地指定一个存放地点。syslog使用UDP 514/TCP 514端口。 1.环境信息 环境信息 HostnameIpAddressOS versionModuleNoterh…...

美国Embarcadero公司正式发布2023 RAD Studio Delphi C++ Builder 12 Athens
Embarcadero 非常高兴地宣布发布 RAD Studio 12 Athens 以及 Delphi 12 和 CBuilder 12。RAD Studio 12 Athens 版本包含令人兴奋的新功能,为该产品的未来奠定了基础。 目录 主要新功能 C 的奇妙之处Delphi 的一些不错的补充FireMonkey 和 Skia 作为新基金会采用 MD…...

树莓派4B的测试记录(CPU、FFMPEG)
本文是用来记录树莓派 4B 的一些测试记录。 温度 下面记录中的风扇和大风扇是这样的: 为什么要用大风扇呢?因为小风扇在外壳上,气流通过外壳的珊格会有啸叫,声音不大但是很烦人,大风扇没这个问题,并且同样…...

物联网AI MicroPython学习之语法 二进制与ASCII转换
学物联网,来万物简单IoT物联网!! ubinascii 介绍 ubinascii模块实现了二进制数据与各种ASCII编码之间的转换。 接口说明 a2b_base64 - 解码base64编码的数据 函数原型:ubinascii.a2b_base64(data)注意事项: 在解码…...
学之思项目的搭建部署 打jar包失败的解决方法
学之思系统介绍部署java环境安装maven安装node.js前端打包工具命令npmGit命令获取源代码安装配置mysql前端打包打包jar包服务上线!!!打jar包失败的解决方法 学之思系统介绍 学之思开源考试系统是一款 java vue 的前后端不分离的考试系统。主要优点是开发、部署简单快捷、界面…...
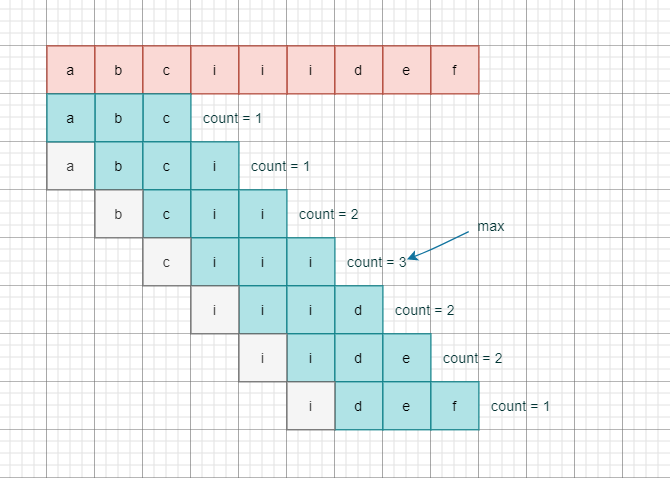
[100天算法】-定长子串中元音的最大数目(day 67)
题目描述 给你字符串 s 和整数 k 。请返回字符串 s 中长度为 k 的单个子字符串中可能包含的最大元音字母数。英文中的 元音字母 为(a, e, i, o, u)。示例 1:输入:s "abciiidef", k 3 输出:3 解释…...
Elastic Observability 8.11:ES|QL、APM 中的通用分析和增强的 SLOs
作者:Tom Grabowski, Katrin Freihofner, Israel Ogbole Elastic Observability 8.11 引入了 ES|QL for Observability(技术预览版)、Universal ProfilingTM 和 Elastic APM 集成,以及针对 Elastic Observability 的新 SLO &#…...
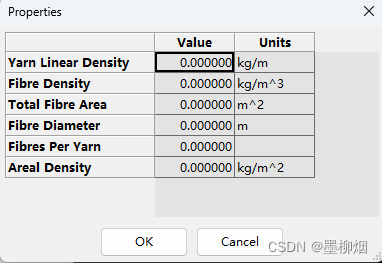
TexGen简单模型对应inp文件简单梳理-2
模型 默认最简单的编织复材,编辑材料属性时发现基体属性设置正常,各向同性材料,但是纱线的材料属性却没有弹性性能的设置。 导出inp文件后,导入ABAQUS中其实可以看到有两种材料,纱线也是有属性的。 ABAQUS中修改属性的…...

VUE获取当前日期的周日和周六
<template><div><div click"handleLast()">上一周</div><div click"handleNext()">下一周</div><el-calendarref"monChild"v-model"value":first-day-of-week"7":range"[sta…...

K8S篇之k8s containerd模式fail to pull image certificate signed by unknown authority
"k8s containerd模式fail to pull image certificate signed by unknown authority"的问题 解决方案:您有两个选择:配置证书或禁用证书验证。 配置证书:您可以为 containerd 配置证书,使其信任由未知机构签名的证书。 具…...
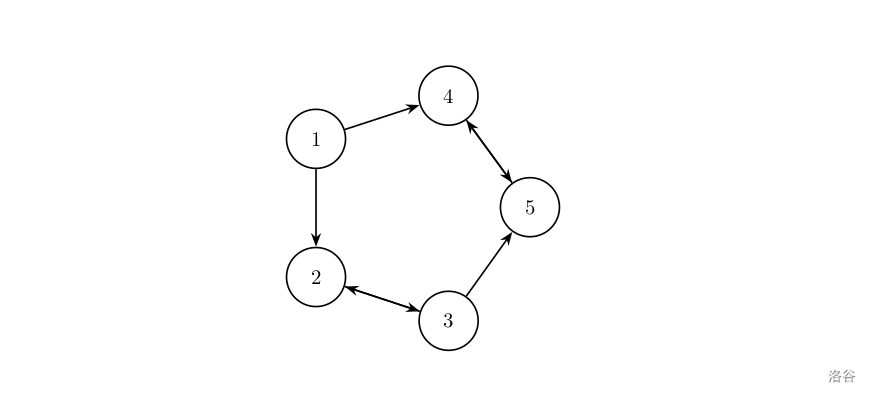
算法进阶指南图论 最优贸易
最优贸易 题目描述 C C C 国有 n n n 个大城市和 m m m 条道路,每条道路连接这 n n n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m m m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
