算法进阶指南图论 最优贸易
最优贸易
题目描述
C C C 国有 n n n 个大城市和 m m m 条道路,每条道路连接这 n n n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m m m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为 1 1 1 条。
C C C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 C C C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设 C C C 国 n n n 个城市的标号从 1 ∼ n 1\sim n 1∼n,阿龙决定从 1 1 1 号城市出发,并最终在 n n n 号城市结束自己的旅行。在旅游的过程中,任何城市可以重复经过多次,但不要求经过所有 n n n 个城市。阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品――水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。由于阿龙主要是来 C C C 国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
假设 C C C 国有 5 5 5 个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路为单向通行,双向箭头表示这条道路为双向通行。
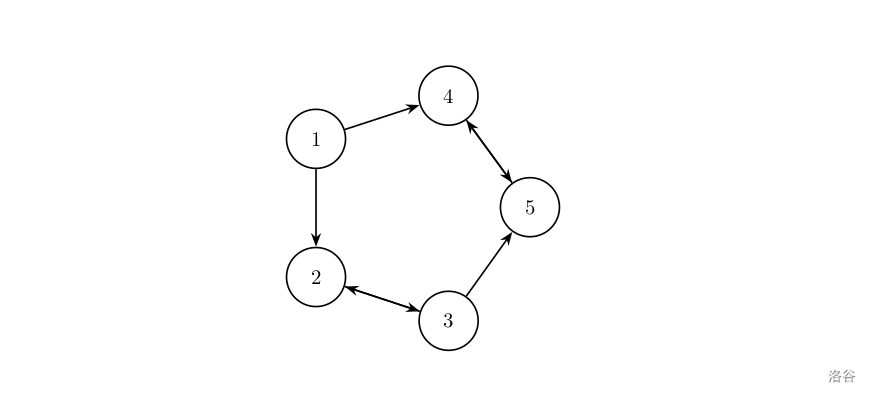
假设 1 ∼ n 1\sim n 1∼n 号城市的水晶球价格分别为 4 , 3 , 5 , 6 , 1 4,3,5,6,1 4,3,5,6,1。
阿龙可以选择如下一条线路: 1 → 2 → 3 → 5 1\to2\to3\to5 1→2→3→5,并在 2 2 2 号城市以 3 3 3 的价格买入水晶球,在 3 3 3 号城市以 5 5 5 的价格卖出水晶球,赚取的旅费数为 2 2 2。
阿龙也可以选择如下一条线路: 1 → 4 → 5 → 4 → 5 1\to4\to5\to4\to5 1→4→5→4→5,并在第 1 1 1 次到达 5 5 5 号城市时以 1 1 1 的价格买入水晶球,在第 2 2 2 次到达 4 4 4 号城市时以 6 6 6 的价格卖出水晶球,赚取的旅费数为 5 5 5。
现在给出 n n n 个城市的水晶球价格, m m m 条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。请你告诉阿龙,他最多能赚取多少旅费。
输入格式
第一行包含 2 2 2 个正整数 n n n 和 m m m,中间用一个空格隔开,分别表示城市的数目和道路的数目。
第二行 n n n 个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这 n n n 个城市的商品价格。
接下来 m m m 行,每行有 3 3 3 个正整数 x , y , z x,y,z x,y,z,每两个整数之间用一个空格隔开。如果 z = 1 z=1 z=1,表示这条道路是城市 x x x 到城市 y y y 之间的单向道路;如果 z = 2 z=2 z=2,表示这条道路为城市 x x x 和城市 y y y 之间的双向道路。
输出格式
一个整数,表示最多能赚取的旅费。如果没有进行贸易,则输出 0 0 0。
样例 #1
样例输入 #1
5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2
样例输出 #1
5
提示
【数据范围】
输入数据保证 1 1 1 号城市可以到达 n n n 号城市。
对于 10 % 10\% 10% 的数据, 1 ≤ n ≤ 6 1\leq n\leq 6 1≤n≤6。
对于 30 % 30\% 30% 的数据, 1 ≤ n ≤ 100 1\leq n\leq 100 1≤n≤100。
对于 50 % 50\% 50% 的数据,不存在一条旅游路线,可以从一个城市出发,再回到这个城市。
对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 100000 1\leq n\leq 100000 1≤n≤100000, 1 ≤ m ≤ 500000 1\leq m\leq 500000 1≤m≤500000, 1 ≤ x , y ≤ n 1\leq x,y\leq n 1≤x,y≤n, 1 ≤ z ≤ 2 1\leq z\leq 2 1≤z≤2,$1\leq $ 各城市的编号 ≤ n \leq n ≤n。
水晶球价格 ≤ 100 \leq 100 ≤100。
思路一:
考虑分层图,因为每个点有两种状态,为买入和卖出,所以我们可以建三层图,平行层之间的边权为0,从第一层到 第二层由当前点 u u u向 u + n u+n u+n连一条边,表示买入,边权为 − w -w −w,同理,我们由 u + n u+n u+n向 u + n ∗ 2 u+n*2 u+n∗2连一条价值为 w w w的边,表示卖出。然后对整个图去跑最长路即可(因为题目说要价值最大)
#include <bits/stdc++.h>using namespace std;
const int N = 1e5 + 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<ll, 3> p3;
int mod = 1e9+7;
const int maxv = 4e6 + 5;
// #define endl "\n"int n,m;vector<pll> e[N];void add(int u,int v,int w)
{e[u].push_back({v,w});
}int st[N];
int d[N];
void spfa()
{memset(d,0x3f,sizeof(d));d[1]=0;queue<int> q;q.push(1);st[1]=1;while(!q.empty()){int t=q.front();q.pop();st[t]=0;int i;for(auto v:e[t]){int b=v.first;int w=v.second;if(d[b]>d[t]+w){d[b]=d[t]+w;if(!st[b]){q.push(b);st[b]=1;}}}}
}void solve()
{cin>>n>>m;vector<int> a(n+5);for(int i=1;i<=n;i++) cin>>a[i],add(i,i+n,-a[i]),add(i+n,i+2*n,a[i]);for(int i=1;i<=m;i++){int x,y,z;cin>>x>>y>>z;add(x,y,0);add(x+n,y+n,0);add(x+n*2,y+n*2,0);if(z==2){add(y,x,0);add(y+n,x+n,0);add(y+n*2,x+n*2,0);}}spfa();cout<<d[n]<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t=1;//cin>>t;while(t--){solve();}system("pause");return 0;
}
思路二:
强连通分量缩点然后进行dp。
初始想法,我们考虑若其为DAG,那么我们可以直接进行DP,但又因为肯定存在环,所以可以对其进行强连通分量缩点。
因为缩完点后为DAG,即有向无环图,而我们对于有向无环图可以直接进行dp,同时我们还可以知道每个强连通分量的最小价值和最大价值,那么我们用dp处理出从 1 号点开始,能到达所有点的最小买入价值,然后用该点的卖出价值减去买入价值,最后对其取max即可。
#include <bits/stdc++.h>using namespace std;
const int N = 1e5 + 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<ll, 3> p3;
int mod = 1e9+7;
// const int maxv = 4e6 + 5;
// #define endl "\n"
int n, m, tot, dfsn[N], ins[N], low[N];
stack<int> s;
vector<int> e[N], e2[N],e3[N];//分别用来存初始图,缩点后的图,缩点后的图对应的反图
vector<vector<int>> scc;
vector<int> b(N);
int a[N];
int minv[N],maxv[N];struct node
{int u,v,z;
}h[N];void dfs(int x)
{low[x] = dfsn[x] = ++tot, ins[x] = 1, s.push(x);for (auto u : e[x]){if (!dfsn[u]){dfs(u);low[x] = min(low[x], low[u]);}else if (ins[u])low[x] = min(low[x], dfsn[u]);}if (dfsn[x] == low[x]){vector<int> c;while (1){auto t = s.top();c.push_back(t);ins[t] = 0;s.pop();b[t] = scc.size();int sz=scc.size();minv[sz]=min(minv[sz],a[t]);maxv[sz]=max(maxv[sz],a[t]);if (t == x)break;}scc.push_back(c);}
}void add(int u, int v)
{e[u].push_back(v);
}bool vis[N];void dfs2(int x)
{vis[x]=1;for(auto u: e3[x])if(!vis[u]) dfs2(u);
}void solve()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=m;i++){int u,v,z;cin>>u>>v>>z;h[i]={u,v,z};add(u,v);if(z==2) add(v,u);}memset(minv,0x3f,sizeof minv);for(int i=1;i<=n;i++){if(!dfsn[i]){dfs(i);}}//缩点过程for(int i=1;i<=m;i++){auto [u,v,z]=h[i];int x=b[u],y=b[v];if(x!=y) {e2[x].push_back(y),e3[y].push_back(x);if(z==2) e2[y].push_back(x),e3[x].push_back(y);//同时注意因为题目中说存在双向边,所以在缩点后的建图中同样也需要建立}}vector<int> dp(n+5);for(int i=0;i<scc.size();i++) dp[i]=minv[i];int st=b[1];int ed=b[n];dfs2(ed);//因为要确保能到达n点,所以从n开始进行dfs搜索能够到达的点,由此需要缩点后的反图int ans=0;for(int i=st;i>=0;i--){//从1号点开始,强连通分量即为逆拓扑序if(vis[i]) {ans=max(ans,maxv[i]-dp[i]);}for(auto u: e2[i]){dp[u]=min(dp[u],dp[i]);}}cout<<ans<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t=1;//cin>>t;while(t--){solve();}system("pause");return 0;
}相关文章:

算法进阶指南图论 最优贸易
最优贸易 题目描述 C C C 国有 n n n 个大城市和 m m m 条道路,每条道路连接这 n n n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m m m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的…...
【Android】Debug时禁用主线程ANR限制
ANR全称Application Not Response,指主线程超过5s无响应,应用会自动退出 由于这个线程,如果我们给主线程加了断点,就会触发ANR,导致调试时应用退出 这样调试起来会非常麻烦,其实对于Debug应用,…...

P6入门:项目初始化1-项目详情介绍
前言 使用项目详细信息查看和编辑有关所选项目的详细信息,在项目创建完成后,初始化项目是一项非常重要的工作,涉及需要设置的内容包括项目名,ID,责任人,日历,预算,资金,分类码等等&…...
进行 “最佳价格查询器” 的开发
前置条件 public class Shop {private final String name;private final Random random;public Shop(String name) {this.name name;random new Random(name.charAt(0) * name.charAt(1) * name.charAt(2));}public double getPrice(String product) {return calculatePrice…...

Brain Teaser概率类 - 三局两胜制
问题 三局两胜制比赛,两局结束还是三局结束的概率大? 解答 假设每局比赛的结果是独立同分布的,且遵循伯努利分布,其中一方的胜率为p,另一方为1-p. 则两局结束的概率是 p 2 ( 1 − p ) 2 ≥ 0.5 p^2 (1-p)^2 \geq …...

在现实生活中传感器GV-H130/GV-21的使用
今天,收获了传感器GV-H130/GV-21,调试探头的用法,下面就来看看吧!如有不妥欢迎指正!!!! 目录 传感器GV-H130/GV-21外观 传感器调试探头 探头与必要准备工作 传感器数值更改调试 …...

海康Visionmaster-全局脚本:通过通讯触发快速匹配 模块换型的方法
如何实现根据通讯信号切换快速匹配的模型文件并触发流程执行? 1.动态切换模板需在全局脚本中调用相关接口实现,可以在全局脚本的通讯数据接收回调中实现代码逻辑,代码如下。 C# using System; using VM.GlobalScript.Methods; using System.…...

什么是闭包
闭包是指函数在定义时可以访问其词法作用域的能力,即使函数在定义之后被传递到了其他地方执行。它包含了两个主要的特性:函数内部可以访问外部函数作用域中的变量,而这些变量在函数执行完毕后依然保持在内存中。 具体来说,闭包的…...
)
sql6(Leetcode1387使用唯一标识码替换员工ID)
1112-2 代码: INNER JOIN 如果表中有至少一个匹配,则返回行 LEFT JOIN 即使右表中没有匹配,也从左表返回所有的行(LEFT为基准 RIGHT JOIN 即使左表中没有匹配,也从右表返回所有的行 # Write your MySQL query st…...

qt-C++笔记之Qt中的时间与定时器
qt-C笔记之Qt中的时间与定时器 code review! 文章目录 qt-C笔记之Qt中的时间与定时器一.Qt中的日期时间数据1.1.QTime:获取当前时间1.2.QDate:获取当前日期1.3.QDateTime:获取当前日期和时间1.4.QTime类详解1.5.QDate类详解1.6..QDateTime类…...

【C++】复杂的多继承及其缺陷(菱形继承)
本篇要分享的内容是C中多继承的缺陷:菱形继承。 以下为本篇目录 目录 1.多继承的缺陷与解决方法 2.虚继承的底层原理 3.虚继承底层原理的设计原因 1.多继承的缺陷与解决方法 首先观察下面的图片判断它是否为多继承 这实际上是一个单继承,单继承的特…...

esp32-rust-no_std-examples-blinky
什么是裸机环境? 裸机环境是指没有可供使用的操作系统环境。当编译的 Rust 程序拥有 no_std 属性时,该程序无权访问上述 std 章节中提到的某些特定功能。尽管仍支持使用配网或引入复杂数据结构等功能,但实现方式将会更加复杂。 no_std…...

GitHub上的开源工业软件
github上看到一个中国人做的流体力学开源介绍,太牛了! https://github.com/clatterrr/FluidSimulationTutorialsUnity 先分析一下工业仿真软件赛道 工业仿真软件的赛道和产品主要功能如下: 1. 工艺仿真赛道: - 工厂布局优化&am…...
Centos7安装配置中文输入法
Centos7安装配置中文输入法 在安装CentOS时,我们为了方便使用,语言选择了中文,但是我们发现,在Linux命令行或者是浏览器中输入时,我们只能输入英文,无法输入汉字。 来,跟随脚步,设…...

【OJ比赛日历】快周末了,不来一场比赛吗? #11.11-11.17 #12场
CompHub[1] 实时聚合多平台的数据类(Kaggle、天池…)和OJ类(Leetcode、牛客…)比赛。本账号会推送最新的比赛消息,欢迎关注! 以下信息仅供参考,以比赛官网为准 目录 2023-11-11(周六) #5场比赛2023-11-12…...

提取当前文件夹下多文件夹中的数据
提取当前文件夹下多文件夹中的数据 1.实现步骤 现在D:\临时\图库 这个文件夹下有多个文件夹,现在需要将多个文件夹中的文件全部移动到D:\临时\图库下; $sourcePath "D:\临时\图库" $targetPath "D:\临时\图库"Get-ChildItem -Path $sourcePath -File …...

深度学习(生成式模型)——Classifier Free Guidance Diffusion
文章目录 前言推导流程训练流程测试流程 前言 在上一节中,我们总结了Classifier Guidance Diffusion,其有两个弊端,一是需要额外训练一个分类头,引入了额外的训练开销。二是要噪声图像通常难以分类,分类头通常难以学习…...
C语言 每日一题 11.9 day15
数组元素循环右移问题 一个数组A中存有N( > 0)个整数,在不允许使用另外数组的前提下,将每个整数循环向右移M(≥0)个位置,即将A中的数据由(A0A1⋯AN−1)变换为&…...
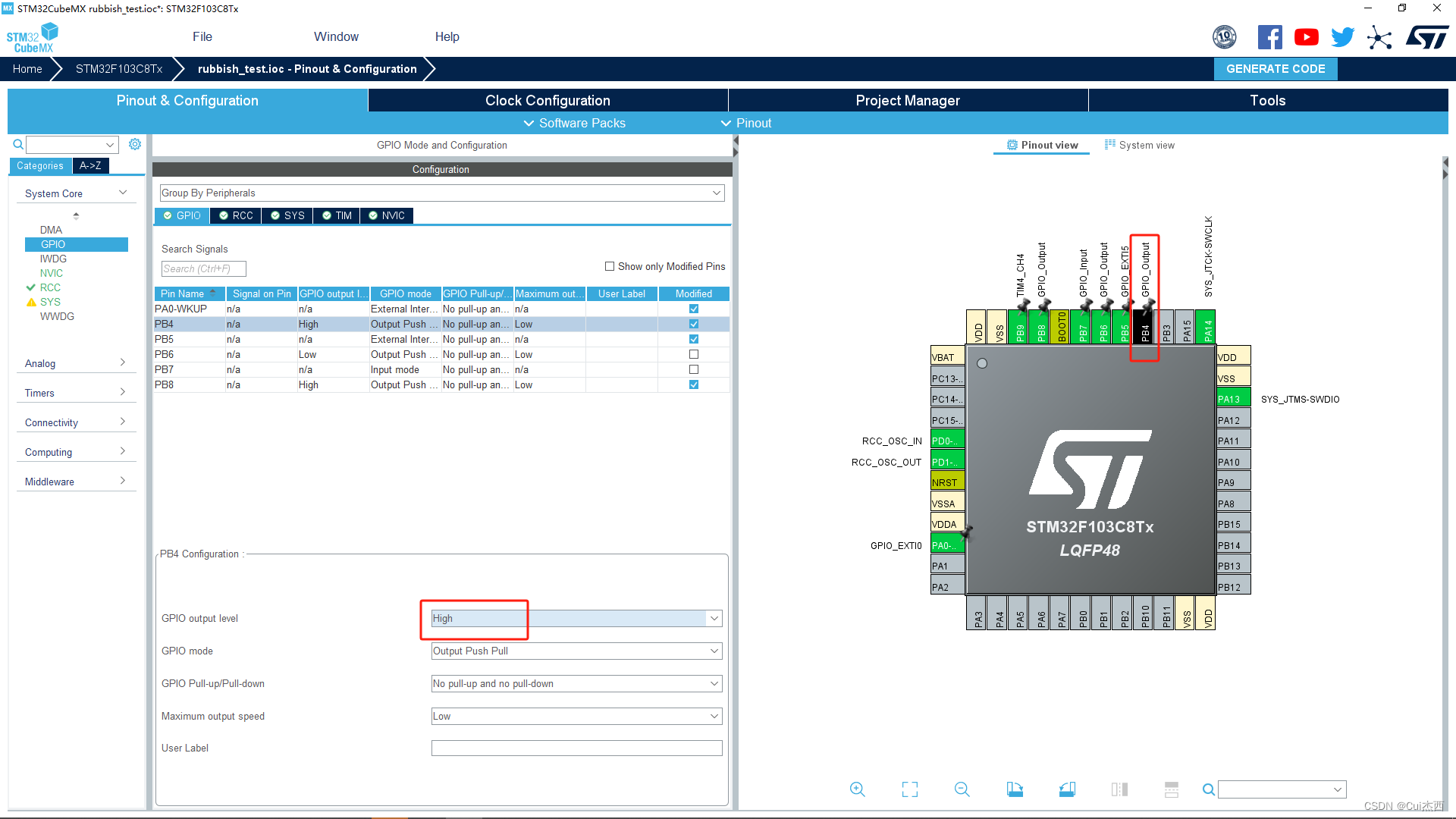
STM32F103C8T6第三天:pwm、sg90、超声波、距离感应按键开盖震动开盖蜂鸣器
1. 定时器介绍1(317.21) 软件定时(之前的定时方法)(软件延时)缺点:不精确、占用CPU资源 void Delay500ms() //11.0592MHz {unsigned char i, j, k;_nop_();i 4;j 129;k 119;do{do{while (-…...
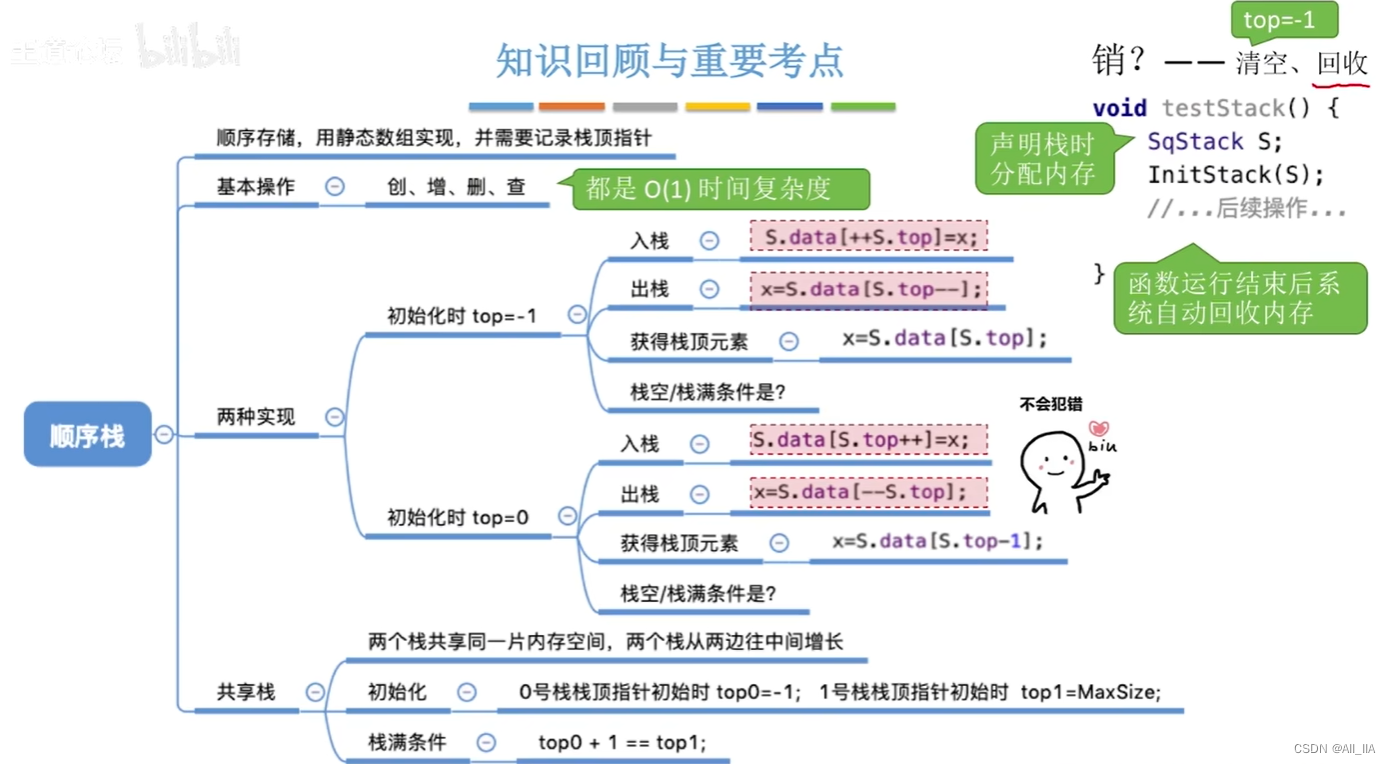
栈的顺序存储实现(C语言)(数据结构与算法)
栈的顺序存储实现通常使用数组来完成。实现方法包括定义一个固定大小的数组,以及一个指向栈顶的指针。当元素入栈时,指针加一并将元素存储在相应位置;当元素出栈时,指针减一并返回相应位置的元素。 1. 顺序栈定义 #define MaxSi…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
