深度学习(生成式模型)——Classifier Free Guidance Diffusion
文章目录
- 前言
- 推导流程
- 训练流程
- 测试流程
前言
在上一节中,我们总结了Classifier Guidance Diffusion,其有两个弊端,一是需要额外训练一个分类头,引入了额外的训练开销。二是要噪声图像通常难以分类,分类头通常难以学习,影响生成图像的质量。
Classifier Free Guidance Diffusion解决了上述两个弊端,不需要引入额外的分类头即可控制图像的生成。
本节所有符号含义与前文一致,请读者阅读完前三篇博文后在查阅此文。
本文仅总结backbone为DDIM情况下的Classifier Free Guidance Diffusion
推导流程
依据前文可知Classifier Guidance Diffusion的前向过程与反向过程与DDPM一致,且有
q ( x t ∣ x t − 1 , y ) = q ( x t ∣ x t − 1 ) q(x_t|x_{t-1},y)=q(x_t|x_{t-1}) q(xt∣xt−1,y)=q(xt∣xt−1)
则有 q ( x t ∣ x 0 , y ) = q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q(x_t|x_{0},y)=q(x_t|x_0)=\mathcal N(x_t;\sqrt{\bar \alpha_t}x_0,(1-\bar\alpha_t)\mathcal I) q(xt∣x0,y)=q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)
假设目前有一批基于条件 y y y的样本 x t x_t xt, ϵ ( x t , t , y ) \epsilon(x_t,t,y) ϵ(xt,t,y)服从标准正态分布,则样本 x t x_t xt将满足
x t = α ˉ t x 0 + 1 − α ˉ t ϵ ( x t , t , y ) (1.0) x_t=\sqrt{\bar \alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon(x_t,t,y)\tag{1.0} xt=αˉtx0+1−αˉtϵ(xt,t,y)(1.0)
依据Tweedie方法,我们有
α ˉ t x 0 = x t + ( 1 − α ˉ t ) ∇ x t log p ( x t ∣ y ) \begin{aligned} \sqrt{\bar \alpha_t}x_0=x_t+(1-\bar\alpha_t)\nabla_{x_t}\log p(x_t|y) \end{aligned} αˉtx0=xt+(1−αˉt)∇xtlogp(xt∣y)
进而有
x t = α ˉ t x 0 − ( 1 − α ˉ t ) ∇ x t log p ( x t ∣ y ) (1.1) x_t=\sqrt{\bar \alpha_t}x_0-(1-\bar\alpha_t)\nabla_{x_t}\log p(x_t|y)\tag{1.1} xt=αˉtx0−(1−αˉt)∇xtlogp(xt∣y)(1.1)
结合式1.0与1.1,则有
∇ x t log p ( x t ∣ y ) = − 1 1 − α ˉ t ϵ ( x t , t , y ) (1.2) \nabla_{x_t}\log p(x_t|y)=-\frac{1}{\sqrt{1-\bar\alpha_t}}\epsilon(x_t,t,y)\tag{1.2} ∇xtlogp(xt∣y)=−1−αˉt1ϵ(xt,t,y)(1.2)
依据贝叶斯公式,我们有
log p ( x t ∣ y ) = log p ( y ∣ x t ) + log p ( x t ) − log p ( y ) ∇ x t log p ( y ∣ x t ) = ∇ x t log p ( x t ∣ y ) − ∇ x t log p ( x t ) + ∇ x t log p ( y ) = ∇ x t log p ( x t ∣ y ) − ∇ x t log p ( x t ) = − 1 1 − α ˉ t ϵ ( x t , t , y ) + 1 1 − α ˉ t ϵ ( x t , t ) (1.3) \begin{aligned} \log p(x_t|y)&=\log p(y|x_t)+\log p(x_t)-\log p(y)\\ \nabla_{x_t}\log p(y|x_t)&=\nabla_{x_t}\log p(x_t|y)-\nabla_{x_t}\log p(x_t)+\nabla_{x_t}\log p(y)\\ &=\nabla_{x_t}\log p(x_t|y)-\nabla_{x_t}\log p(x_t)\\ &=-\frac{1}{\sqrt{1-\bar\alpha_t}}\epsilon(x_t,t,y)+\frac{1}{\sqrt{1-\bar\alpha_t}}\epsilon(x_t,t) \end{aligned}\tag{1.3} logp(xt∣y)∇xtlogp(y∣xt)=logp(y∣xt)+logp(xt)−logp(y)=∇xtlogp(xt∣y)−∇xtlogp(xt)+∇xtlogp(y)=∇xtlogp(xt∣y)−∇xtlogp(xt)=−1−αˉt1ϵ(xt,t,y)+1−αˉt1ϵ(xt,t)(1.3)
回顾一下backbone为DDIM的Classifier Guidance Diffusion的采样流程

将式1.3代入,且引入一个超参数 w w w,可得
ϵ ^ = ϵ θ ( x t ) − w 1 − α ˉ t ∇ x t log p ( y ∣ x t ) = ϵ θ ( x t ) − w ( ϵ θ ( x t , t ) − ϵ θ ( x t , t , y ) ) = ( 1 − w ) ϵ θ ( x t , t ) + w ϵ θ ( x t , t , y ) (1.4) \begin{aligned} \hat \epsilon &= \epsilon_\theta(x_t)-w\sqrt{1-\bar\alpha_t}\nabla_{x_t}\log p(y|x_t)\\ &=\epsilon_\theta(x_t)-w(\epsilon_\theta(x_t,t)-\epsilon_\theta(x_t,t,y))\\ &=(1-w)\epsilon_\theta(x_t,t)+w\epsilon_\theta(x_t,t,y) \end{aligned}\tag{1.4} ϵ^=ϵθ(xt)−w1−αˉt∇xtlogp(y∣xt)=ϵθ(xt)−w(ϵθ(xt,t)−ϵθ(xt,t,y))=(1−w)ϵθ(xt,t)+wϵθ(xt,t,y)(1.4)
注意到原论文的推导结果为(为了区分,超参数设为 w ^ \hat w w^)
ϵ ^ = ( 1 + w ^ ) ϵ θ ( x t , t , y ) − w ^ ϵ θ ( x t , t ) (1.5) \hat \epsilon = (1+\hat w)\epsilon_\theta(x_t,t,y)-\hat w\epsilon_\theta(x_t,t)\tag{1.5} ϵ^=(1+w^)ϵθ(xt,t,y)−w^ϵθ(xt,t)(1.5)
式1.5和1.4是一致的,均为 ϵ θ ( x t , t , y ) \epsilon_\theta(x_t,t,y) ϵθ(xt,t,y)与 ϵ θ ( x t , t ) \epsilon_\theta(x_t,t) ϵθ(xt,t)的加权和,且权重和为1。
训练流程
依据式1.5,我们需要训练两个神经网络 ϵ θ ( x t , t , y ) \epsilon_\theta(x_t,t,y) ϵθ(xt,t,y)与 ϵ θ ( x t , t ) \epsilon_\theta(x_t,t) ϵθ(xt,t),前者为的输入包含加噪图片 x t x_t xt以及条件 y y y(图像or文字),后者的输入仅包含加噪图像 x t x_t xt。但其实两个神经网络可以共用一个backbone,在训练时,只需要用一定的概率将条件 y y y设置为空即可。
测试流程
Classifier Free Guidance Diffusion的测试流程有两次推断
- 将条件 y y y空置,得到 ϵ θ ( x t , t ) \epsilon_\theta(x_t,t) ϵθ(xt,t)
- 输入条件 y y y,得到 ϵ θ ( x t , t , y ) \epsilon_\theta(x_t,t,y) ϵθ(xt,t,y)
- 利用公式1.5,生成基于条件 y y y的图像
可以看到推断成本多了一倍。
相关文章:

深度学习(生成式模型)——Classifier Free Guidance Diffusion
文章目录 前言推导流程训练流程测试流程 前言 在上一节中,我们总结了Classifier Guidance Diffusion,其有两个弊端,一是需要额外训练一个分类头,引入了额外的训练开销。二是要噪声图像通常难以分类,分类头通常难以学习…...
C语言 每日一题 11.9 day15
数组元素循环右移问题 一个数组A中存有N( > 0)个整数,在不允许使用另外数组的前提下,将每个整数循环向右移M(≥0)个位置,即将A中的数据由(A0A1⋯AN−1)变换为&…...
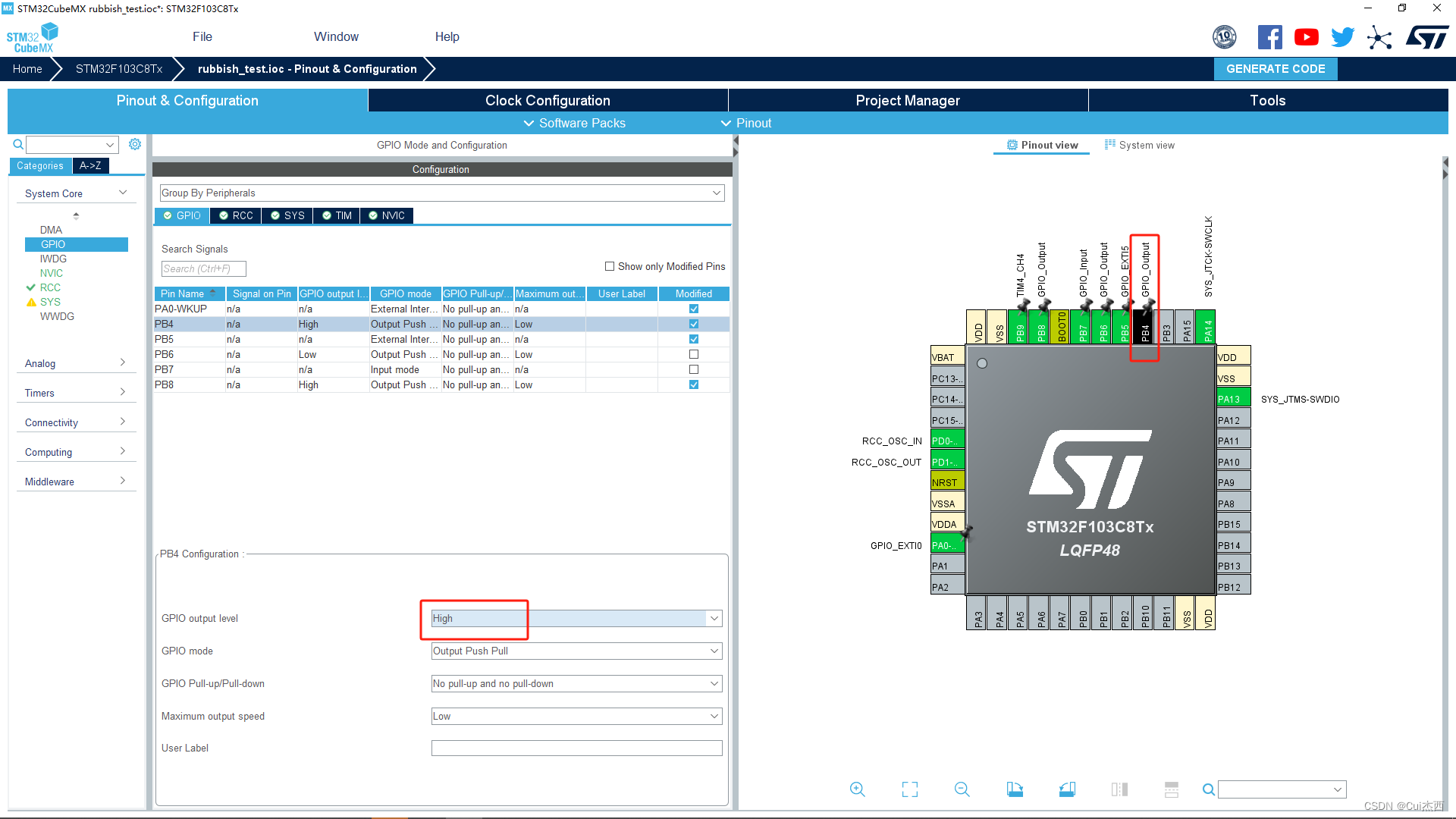
STM32F103C8T6第三天:pwm、sg90、超声波、距离感应按键开盖震动开盖蜂鸣器
1. 定时器介绍1(317.21) 软件定时(之前的定时方法)(软件延时)缺点:不精确、占用CPU资源 void Delay500ms() //11.0592MHz {unsigned char i, j, k;_nop_();i 4;j 129;k 119;do{do{while (-…...
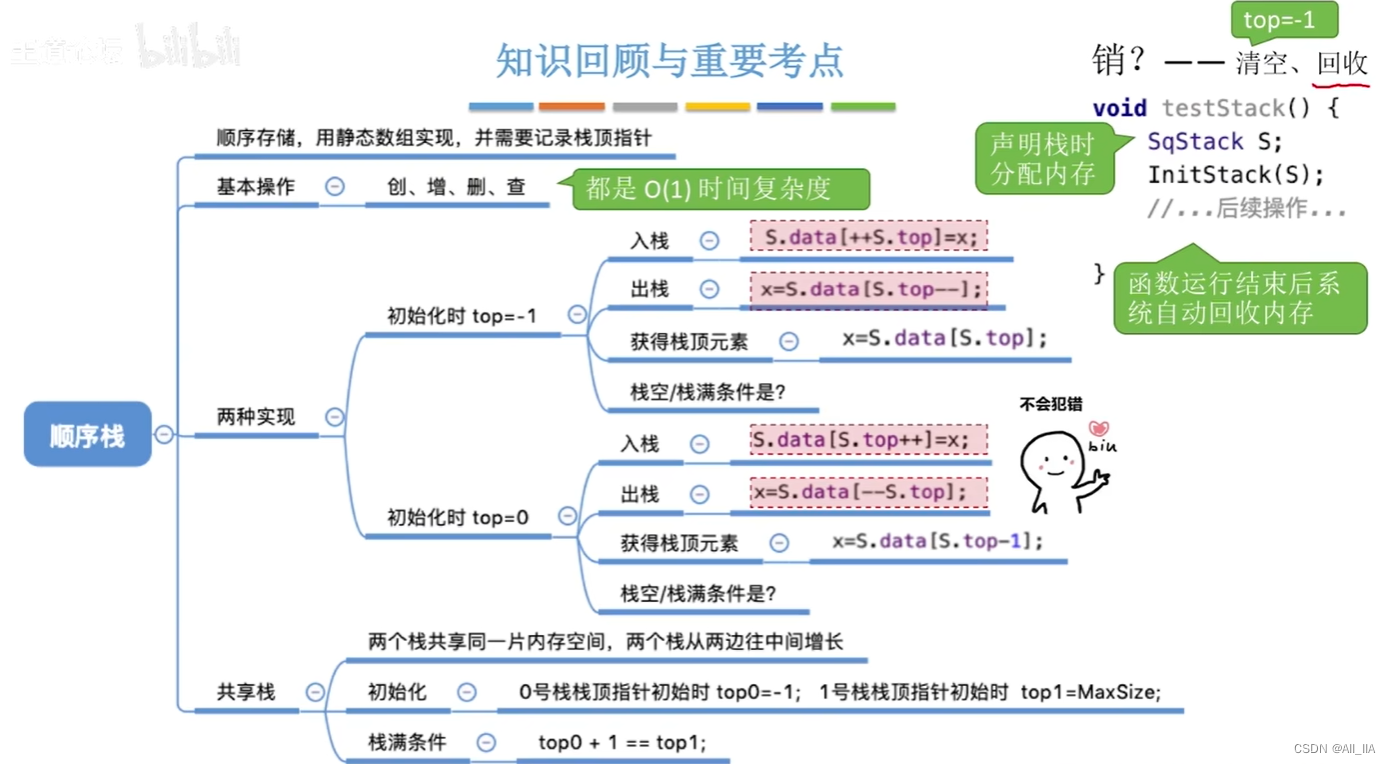
栈的顺序存储实现(C语言)(数据结构与算法)
栈的顺序存储实现通常使用数组来完成。实现方法包括定义一个固定大小的数组,以及一个指向栈顶的指针。当元素入栈时,指针加一并将元素存储在相应位置;当元素出栈时,指针减一并返回相应位置的元素。 1. 顺序栈定义 #define MaxSi…...

设计模式 -- 观察者模式
说明 author blog.jellyfishmix.com / JellyfishMIX - githubLICENSE GPL-2.0 定义 观察者模式(Observer Design Pattern) 也被称为发布订阅模式(Publish-Subscribe Design Pattern)。在 GoF 的《设计模式》一书中,它的定义是这样的: Define a one-to-many depe…...

Go RabbitMQ简介 使用
RabbitMQ简介 RabbitMQ 是一个广泛使用的开源消息队列系统,它实现了高级消息队列协议(AMQP)标准,为分布式应用程序提供了强大的消息传递功能。RabbitMQ 是 Erlang 语言编写的,具有高度的可扩展性和可靠性,…...

【面经】Spring框架中用了哪些设计模式
在Spring框架中,主要运用了以下几种设计模式: 工厂模式: Spring beanFactory使用工厂模式在应用程序中管理对象的创建。 通过使用工厂模式,Spring可以将对象的创建与使用分离,降低耦合度。 单例模式: Spr…...
SpringBoot自动配置的原理篇,剖析自动配置原理;实现自定义启动类!附有代码及截图详细讲解
SpringBoot 自动配置 Condition Condition 是在Spring 4.0 增加的条件判断功能,通过这个可以功能可以实现选择性的创建 Bean 操作 思考:SpringBoot是如何知道要创建哪个Bean的?比如SpringBoot是如何知道要创建RedisTemplate的?…...

苹果Ios系统app应用程序开发者如何获取IPA文件签名证书时需要注意什么?
今天呢想和大家介绍介绍苹果App开发者如何获取IPA文件签名证书的步骤和注意事项。对于苹果应用程序开发者而言,获取IPA文件签名证书是发布应用程序至App Store的重要步骤之一。签名证书能够确保应用程序的安全性和可信度,并使其能够在设备上正确运行。 …...
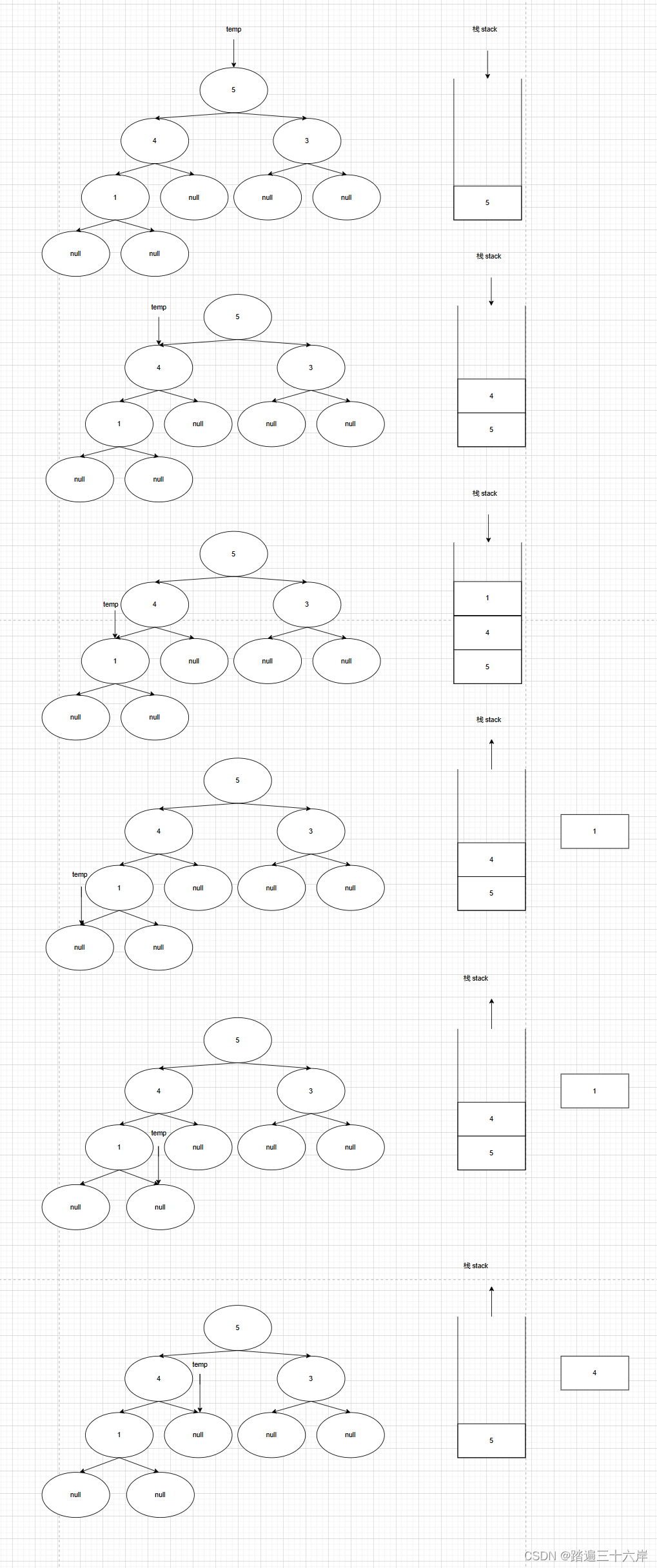
算法通关村第七关-黄金挑战二叉树迭代遍历
大家好我是苏麟 , 今天带来二叉树的迭代遍历 . 二叉树的迭代遍历 前序编列 描述 : 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 题目 : LeetCode 二叉树的前序遍历 : 144. 二叉树的前序遍历 分析 : 前序遍历是中左右,如果还有左子树就一…...
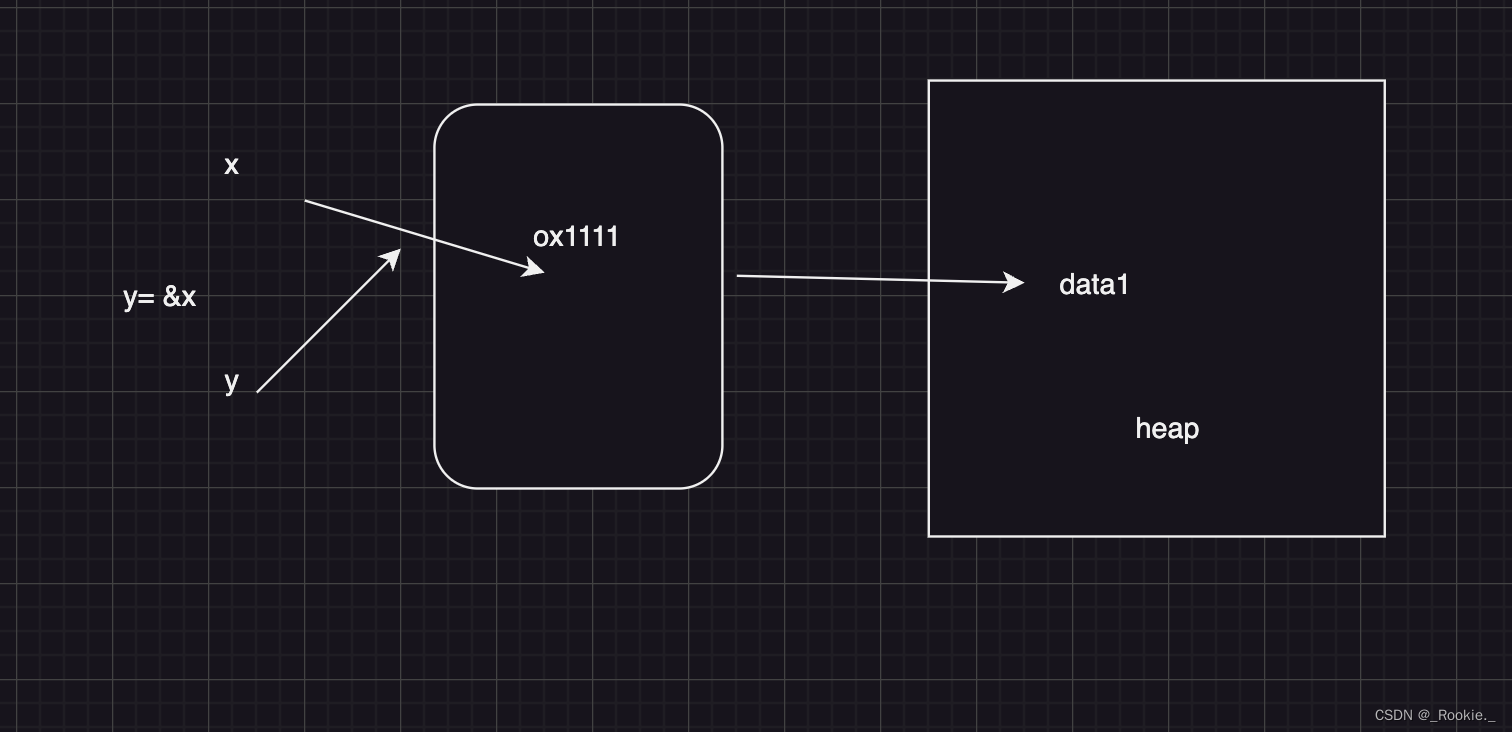
2023-11-Rust
学习方案:Rust程序设计指南 1、变量和可变性 声明变量:let 变量、const 常量 rust 默认变量一旦声明,就不可变(immutable)。当想改变 加 mut(mutable) 。 const 不允许用mut ,只能声明常量,…...

iOS代码混淆----自动
先大致解释一下“编译"、"反编译": 编译:就是把千千万万行字符串(也叫代码,或者源文件),变成010101010101(机器码,也叫目标代码) 编译过程:预处理-编译-汇编-链接 我的脚本运行在预处理阶段。 反编…...
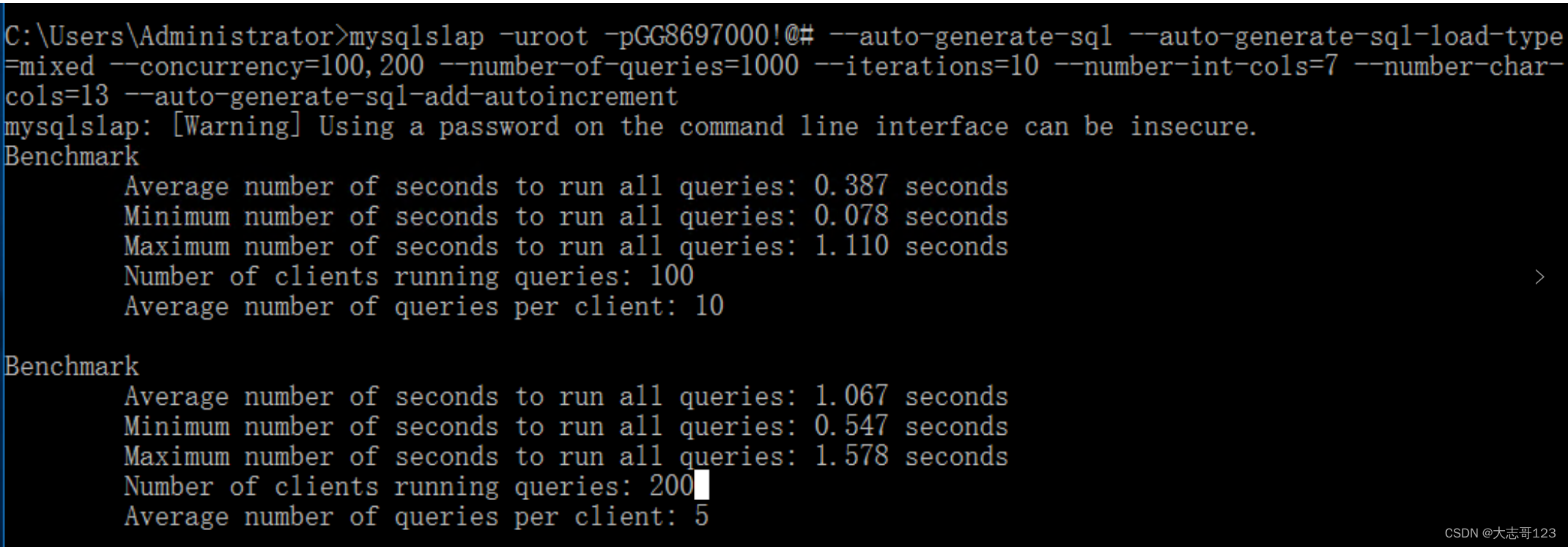
对Mysql和应用微服务做TPS压力测试
1.对Mysql 使用工具:mysqlslap工具 使用命令: mysqlslap -uroot pGG8697000!#--auto generate sql -auto generate sql-load typemixed-concurrency100,200 - number of queries1000-iterations10 - number-int-cols7 - number-charcols13auto genera…...
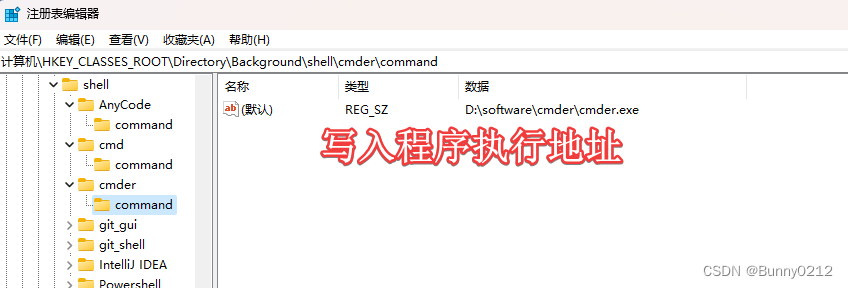
将程序添加至右键菜单
将程序添加至右键菜单 手动导入 如果要将cmder添加至右键菜单。可以通过编写reg注册表方式添加 也可以在路径HKEY_CLASSES_ROOT\Directory\Background\shell中右击添加 创建项commadn 编写reg注册表 [HKEY_CLASSES_ROOT\Directory\Background\shell\cmder]为注册表地址 Wi…...

三板斧的使用、全局配置文件、静态文件的配置、orm介绍
三板斧的使用 【1】HttpResponse 返回字符串类型 【2】render 返回html页面,并且在返回给浏览器之前还可以给html页面传值 【3】redirect 重定向页面 视图函数必须返回一个 HttpResponse 对象 def index(request):print(request)# return HttpResponse("r…...
【编程实践】黑框框里的打字小游戏,但是汇编语言
开始: 在学习王爽的《汇编语言》的过程中,我就真切地体会到编程实践对于理解的帮助。起初我没有安装书中的实验环境,看到100页左右就开始感觉无趣、吃力,看了后面忘前面,差点就要放弃这本书的学习。好在我后来还是装好…...
ElasticSearch的集群、节点、索引、分片和副本
Elasticsearch是面向文档型数据库,一条数据在这里就是一个文档。为了方便大家理解,我们将Elasticsearch里存储文档数据和关系型数据库MySQL存储数据的概念进行一个类比 ES里的Index可以看做一个库,而Types相当于表,Documents则相当…...

std::cout无法打印uint8_t类型的数据
std::cout在处理uint8_t变量类型的时候默认输出字符,刚好数字0-10对应的ascii字符都是不可打印的 解决: 使用static_cast std::cout << static_cast<int>(time) << std::endl;参考文章:https://blog.csdn.net/weixin_459…...
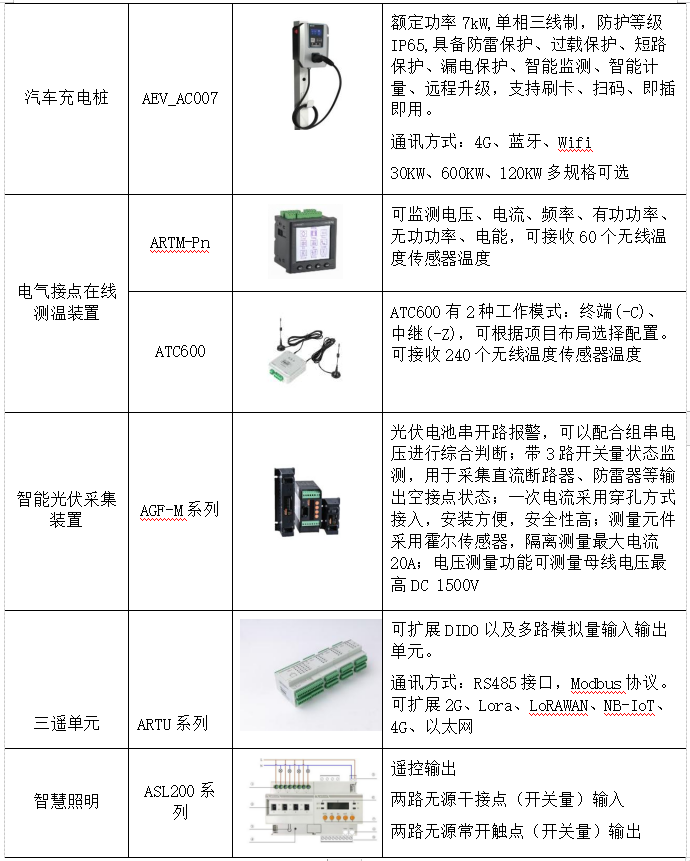
浅谈泛在电力物联网在智能配电系统应用
贾丽丽 安科瑞电气股份有限公司 上海嘉定 201801 摘要:在社会经济和科学技术不断发展中,配电网实现了角色转变,传统的单向供电服务形式已经被双向能流服务形式取代,社会多样化的用电需求也得以有效满足。随着物联网技术的发展&am…...

已解决:云原生领域的超时挂载Bug — Kubernetes深度剖析
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
